一、Aggregate Analysis 综合分析

1.1 主要思想

证明对于含有n个操作的序列，最坏情况下的总时间为T(n)，则每个操作的平均代价为T(n)/n

1.2 实例

证明：一个有多次删除功能的Stack，平均操作成本为O(1)

对于一个初始为空的stack来说，对其进行n个操作(Push、Pop、MultiPop)，stack始终满足sizeof(S) ≤ n

因此，T = O(n)/n = O(1)

二、Accounting method 核算法

2.1 主要思想

当操作的平均成本 > 实际成本时，将差额作为余额存储。余额可以帮助支付以后的操作成本。保证每一步：平均成本 + 余额 > 实际成本

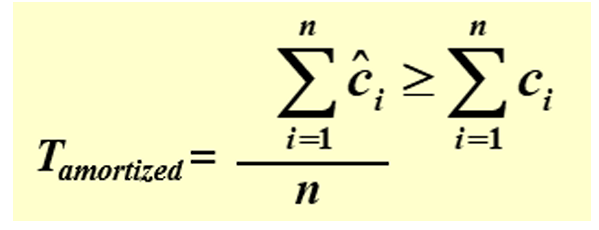
2.2 实例

三、Potential method 潜在法

3.1 主要思想

对于credit有： $$ \[\begin{aligned} \widehat{c}_{i} - {c}_{i} &= Credit_{i} = \phi(D_i) - \phi(D_{i-1}) \\ \sum_{i=1}^{n} \widehat c_i &= \sum_{i=1}^{n} (\widehat c_i + \phi(D_i) - \phi(D_{i-1})) \\ &=(\sum_{i=1}^{n} \widehat c_i ) + \phi(D_i) - \phi(D_0) \\ \end{aligned}\]

因此，只需要保证 $\phi(D_i) - \phi(D_0) \geq 0$

3.2 实例

四、对于Splay树的复杂度证明

4.1 插入

定义： \[ \phi(T) = \sum_{i\in T} log \ s(i) \\ \] 情况1：zig-zig

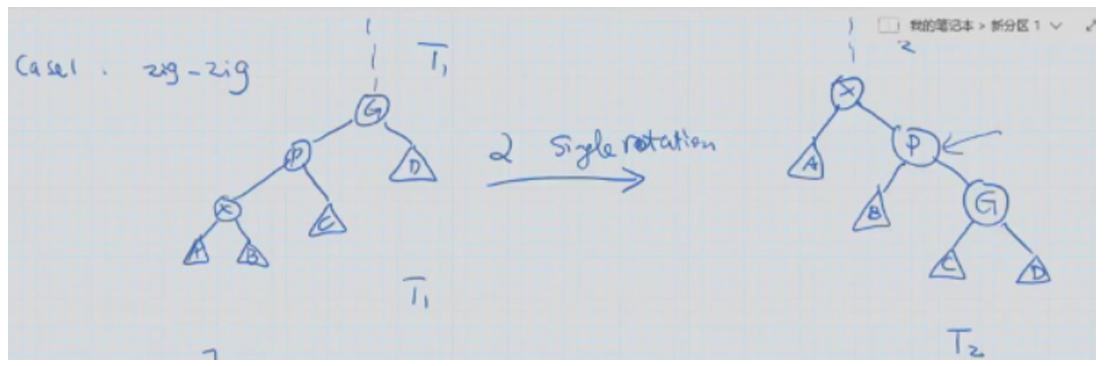$$ \[\begin{aligned} \hat c &= c+\phi(T_2)-\phi(T_1) \\ &=2+R_2(x)+R_2(p)+R_2(G)-R_1(x)-R_1(p)-R_1(G) \\ &\leq 2+R_2(x)+R_2(G)-R_1(x)-R_1(p) \ [\because R_2(p)\leq R_1(G)]\\ &\leq 2+R_2(x)+R_2(G)-2R_1(x) \ [\because R_1(x)<R_1(p)]\\ &\leq 3(R_2(x) - R_1(x)) \end{aligned}\] \[ 最后一步的证明： \] \[\begin{aligned} &要证:2+R_2(x)+R_2(G)-2R_1(x)\leq 3(R_2(x) - R_1(x))\\ &即证:2+R_2(G) \leq 2R_2(x)-R_1(x)\\ &\because 当a+b\leq c时,有log \ a+log \ b-2log \ c \leq-2\\ &\therefore log(1+C+D)+log(1+A+B)-2log(3+A+B+C+D)\leq-2 \\ &\therefore R_2(G)+R_1(x)-2R_2(x)\leq-2 \\ \end{aligned}\]

$$ 情况2：zig-zag

$$ \[\begin{aligned} \hat c &= c+\phi(T_2)-\phi(T_1) \\ &=2+R_2(x)+R_2(p)+R_2(G)-R_1(x)-R_1(p)-R_1(G) \\ &=2+R_2(p)+R_2(G)-2R_1(x)\\ &\leq 2R_2(x)-2R_1(x) \\ &\leq 3(R_2(x)-R_1(x)) \end{aligned}\]

情况3：zig $$ \[\begin{aligned} \hat c &= c+\phi(T_2)-\phi(T_1) \\ &=1+R_2(x)+R_2(p)-R_1(x)-R_1(p) \\ &\leq 1+R_2(x)-R_1(x) \\ &\leq 1+3(R_2(x)-R_1(x)) \end{aligned}\] \[ 对于一次**Splay(x)** \] \[\begin{aligned} \hat c &= \sum_{i=1}^{k} \hat c_i \\ &\leq 1+\sum_{i=1}^{k}3(R_{i}(x)-R_{i-1}(x)) \\ &\leq 1+3(R_k(x) - R_0(x)) \\ \therefore \ &\hat c(O_i) = O(log\ n) \\ &\sum_{i=1}^{m} \hat c(O_i) = \sum_{i=1}^m c_i+\phi(T_m)-\phi(T_0)\\ &\sum_{i=1}^{m} c_i \leq m\ log\ n+n\ log\ n \end{aligned}\]

五、Vector的时间复杂度证明

5.1 插入

设$\Phi(T)=2*num(T)-size(T)$

$num(T)$：表示$T$中包含的元素个数

$size(T)$：表示$T$能够容纳的元素个数

插入：>原有空间时，将空间double

(1)若没有导致内存扩大，则：

$c_i=1$

$\hat c_i=c_i+\Phi_i-\Phi_{i-1}$

$=1+(2num_i-size_i)-(2num_{i-1}-size_{i-1})$

$=3$

(2)若导致了内存扩大，则

$c_i=1+num_{i-1}$

$\hat c_i=c_i+\Phi_i-\Phi_{i-1}$

$=1+(i-1)+(2num_i-size_i)-(2num_{i-1}-size_{i-1})$

$=i+(2i-2(i-1))-(2(i-1)-(i-1))$

$=3$

5.2 删除

删除：<原有空间的1/4时，将空间减半

设$\alpha$：表示$\frac{table中包含的元素个数}{table的大小}$

$\Phi(T)=2num(T)-size(T)\ \alpha>=1/2$

$=size(T)/2-num(T)\ \alpha\leq1/2$