ADS01：平衡树(含实现)--AVL树

一、性质

1. 是一个二叉搜索树
2. 左右子树高度之差的绝对值$$1
3. 设\(n_h\)为高度为\(h\)的AVL树的最小节点数，则\(n_h = n_{h-1}+n_{h-2}+1\)
   1. 可以求得，\(n_h=Fibonacci_{h+2}-1\)
   2. \(Fibonacci_{h+2} ≈ \frac{1}{\sqrt5}(\frac{1+\sqrt 5}{2})^i\)

二、插入

2.1 BST 插入

正常进行BST的插入操作，然后按照以下步骤调整AVL的平衡性

2.2 平衡调整

• 找到平衡因子为±2的节点
  • 平衡因子 = 左子树高度 - 右子树高度
• 找插入新节点后，失去平衡的最小子树（只考虑3个节点）
  • 距离插入节点最近
  • 以平衡因子为±2的节点作为根
  • 子节点的平衡因子为±1
• 是哪一种类型，要根据 平衡因子为±2的节点 与 插入的节点 的相对位置来判断

2.2.1 LL型：右旋

• B为根，B的右子树变为A的左子树（中为支，高右转）

2.2.2 RR型：左旋

• B为根，B的左子树变为A的右子树（中为支，高左转）

2.2.3 LR型：左右旋

• C为根，C的左子树变为B的右子树，C的右子树变为A的左子树（下二整体先左转，后与LL同）

2.2.4 RL型：右左旋

• C为根，C的左子树变为A的右子树，C的右子树变为B的左子树（下二整体先右转，后与RR同）

三、 删除

3.1 BST删除

• 叶节点：直接删除
• 只有一个子节点：直接删除，子节点顶替父节点的位置
• 有两个子节点：以下两种方法选一个即可
  • 找左子树的最右节点，顶替父节点的位置，然后删掉左子树的最右节点
  • 找右子树的最左节点，顶替父节点的位置，然后删掉右子树的最左节点

3.2 平衡调整

• 因为删除的是右子树中的节点，因此只可能是右子树的深度-1
• 左子树比右子树深2，因此只需要右旋一次即可

四、代码实现

4.1 旋转

AVL* RotateLeft(AVL* root) {//左旋,根的右儿子变成根,根变为左儿子
	AVL* temp = root->rch;
	root->rch = temp->lch;
	temp->lch = root;

	//更新树的高度
	//只有被操作的两个节点(root,temp=root->rch)的高度会改变
	//由于新树中temp为根,root为子节点,故先更新root的高度
	Update(root);
	Update(temp);
	return temp;
}
AVL* RotateRight(AVL* root) {//右旋,根的左儿子变为根,根变为右儿子
	AVL* temp = root->lch;
	root->lch = temp->rch;
	temp->rch = root;
	//更新树的高度
	//只有被操作的两个节点(root,temp=root->rch)的高度会改变
	//由于新树中temp为根,root为子节点,故先更新root的高度
	Update(root);
	Update(temp);
	return temp;
}
AVL* RotateLeftRight(AVL* root) {//左右旋,先左旋左儿子,再右旋根
	root->lch = RotateLeft(root->lch);
	root = RotateRight(root);
	return root;
}
AVL* RotateRightLeft(AVL* root) {//右左旋,先右旋右儿子,再左旋根
	root->rch = RotateRight(root->rch);
	root = RotateLeft(root);
	return root;
}

4.2 插入

AVL* Insert(AVL* root, int data) {//插入data
	if (root == NULL) {
		root = new AVL();
		root->data = data;
		root->lch = NULL;
		root->rch = NULL;
		root->height = 1;
		root->sum = 1;
		root->size = 1;
		return root;
	}
	else if (data == root->data) {
		root->sum++;
		root->size++;
		return root;
	}
	else if (data < root->data) {//data插入到左子树
		root->lch = Insert(root->lch, data);
		Update(root);
		//因为插入在左子树,因此只可能是左子树的深
		if (root != NULL && GetBalance(root) == 2) {//左子树过深
			if (GetBalance(root->lch) == -1) {//LR型
				root = RotateLeftRight(root);
			}
			else {//LL型
				root = RotateRight(root);
			}
		}
	}
	else {
		root->rch = Insert(root->rch, data);
		Update(root);
		//因为插入在右子树,因此只可能是右子树深
		if (root != NULL && GetBalance(root) == -2) {//右子树过深
			if (GetBalance(root->rch) == 1) {//RL型
				root = RotateRightLeft(root);
			}
			else {//RR型
				root = RotateLeft(root);
			}
		}
	}
	return root;
}

4.3 删除

AVL* Delte(AVL* root, int key, int delta) {
	if (root == NULL)return NULL;	
	if (key < root->data) {
		root->lch = Delte(root->lch, key, delta);
		Update(root);
		//因为删除的是左子树中的节点,因此只可能是左子树的浅
		if (root != NULL && GetBalance(root) == -2) {//右子树过深
			if (GetBalance(root->rch) == 1) {//RL型
				root = RotateRightLeft(root);
			}
			else {//RR型
				root = RotateLeft(root);
			}
		}
		return root;
	}
	else if (key > root->data) {
		root->rch = Delte(root->rch, key, delta);
		Update(root);
		//因为删除的是右子树中的节点,因此只可能是右子树浅
		if (root != NULL && GetBalance(root) == 2) {//左子树过深
			if (GetBalance(root->lch) == -1) {//LR型
				root = RotateLeftRight(root);
			}
			else {//LL型
				root = RotateRight(root);
			}
		}
		return root;
	}
	else {//找到该值,进行删除操作
		root->sum -= delta;
		root->size -= delta;
		if (root->sum > 0)return root;
		if (root->lch != NULL && root->rch != NULL) {//不是叶节点
			AVL* temp = FindNext(root, key);//找到比key大的最小的数
			root->data = temp->data;
			root->sum = temp->sum;//将后继节点替换当前节点
			root->rch = Delte(root->rch, temp->data, Inf);
			Update(root);
			//因为删除的是右子树中的节点,因此只可能是右子树的深度-1
			if (root != NULL && GetBalance(root) == 2) {//左子树过深
				if (GetBalance(root->lch) == -1) {//LR型
					root = RotateLeftRight(root);
				}
				else {//LL型
					root = RotateRight(root);
				}
			}
			return root;
		}
		else {//删除的点的度数为0/1
			AVL* temp = root;
			if (root->lch == NULL)root = root->rch;
			else if (root->rch == NULL)root = root->lch;
			delete temp;
			Update(root);
			return root;
		}
	}
}

4.4 查找某数是第几大

int GetRank(AVL* root, int key) {
	if (root == NULL)return 0;
	if (key == root->data)//key == 当前节点的值
		return GetSize(root->lch) + 1;
	else if (key > root->data)//key > 当前节点的值 ==> 在右子树里面
		return GetSize(root->lch) + root->sum + GetRank(root->rch, key);
	else //key < 当前节点的值 ==> 在左子树里面 
		return GetRank(root->lch, key);
}

4.5 找第k大数

AVL* FindByRank(AVL* root, int rank) {
	if (rank > GetSize(root->lch) + root->sum)//比左子树+自己大 ==> 在右子树里
		return FindByRank(root->rch, rank - GetSize(root->lch) - root->sum);
	else if (rank > GetSize(root->lch))//比左子树大 ==> 就是自己
		return root;
	else//比左子树小 ==> 在左子树里
		return FindByRank(root->lch, rank);
}

4.6 前驱

AVL* FindPre(AVL* root, int key) {//找比key小的最大的数
	AVL* ans = NULL;
	while (root != NULL) {
		if (key <= root->data){//root>key,在左子树,注意等号成立时依旧需要向下找 
			root = root->lch;
		}
		else{//root<key,在右子树 
			if(ans==NULL || ans->data < root->data)ans=root;
			root = root->rch;
		}
	}
	return ans;
}

4.7 后继

AVL* FindNext(AVL* root, int key) {//找比key大的最小的数
	AVL* ans = NULL;
	while (root != NULL) {
		if (key < root->data){//root>key,在左子树 
			if(ans==NULL || ans->data > root->data)ans=root;
			root = root->lch;
		}
		else{//root<key,在右子树,注意等号成立时依旧需要向下找
			root = root->rch;
		}
	}
	return ans;
}

五、作业题

For an AVL tree, the balance factors of all the non-leaf nodes are 0 iff the tree is a complete binary tree.

• 题目意思：对于一棵 AVL 树，当该树是完全二叉树时，所有非叶节点的平衡因子为 0
• 答案：F
• 解答：完全二叉树的最底层不一定是满的，满二叉树的最底层才是满的

完全二叉树：设二叉树的深度为h

• 除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数
• 第 h 层所有的结点都连续集中在最左边

附录 总代码

#pragma warning(disable:4996)
//AVL树
#include <cstdio>
#include <iostream>
#include <cmath>
using namespace std;
struct AVL {
	int data;
	int height;
	int sum;
	int size;
	AVL* lch, * rch;
};
const int Inf = 1e5;
AVL* root = NULL;
int GetHeight(AVL*);
int GetBalance(AVL*);
int GetSize(AVL*);
void Update(AVL*);
AVL* RotateLeft(AVL*);
AVL* RotateRight(AVL*);
AVL* RotateLeftRight(AVL*);
AVL* RotateRightLeft(AVL*);

AVL* Insert(AVL*, int);
AVL* Delte(AVL*, int, int);
int  GetRank(AVL*, int);
AVL* FindByRank(AVL*, int);
AVL* FindPre(AVL*, int);
AVL* FindNext(AVL*, int);
int main() {
	//freopen("1.in","r",stdin);
	//freopen("out.txt", "w", stdout);
	int n, op, x;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%d%d", &op, &x);
		AVL* temp = NULL;
		if (op == 1)root = Insert(root, x);
		else if (op == 2)root = Delte(root, x, 1);
		else if (op == 3)printf("%d\n", GetRank(root, x));
		else if (op == 4)temp = FindByRank(root, x);
		else if (op == 5)temp = FindPre(root, x);
		else if (op == 6)temp = FindNext(root, x);
		if (temp != NULL)printf("%d\n", temp->data);
	}
	return 0;
}
int GetHeight(AVL* root) {
	if (root == NULL)return 0;
	else return root->height;
}
int GetBalance(AVL* root) {
	if (root == NULL)return 0;
	else return GetHeight(root->lch) - GetHeight(root->rch);
}
int GetSize(AVL* root) {
	if (root == NULL)return 0;
	else return root->size;
}
void Update(AVL* root) {
	if (root == NULL)return;
	root->height = max(GetHeight(root->lch), GetHeight(root->rch)) + 1;
	root->size = GetSize(root->lch) + GetSize(root->rch) + root->sum;
}
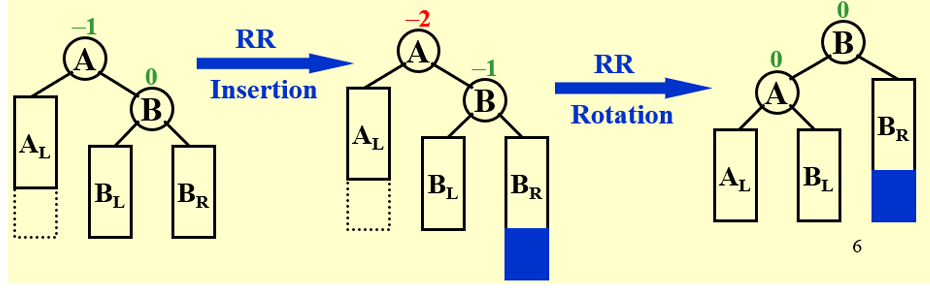
AVL* RotateLeft(AVL* root) {//左旋,根的右儿子变成根,根变为左儿子
	AVL* temp = root->rch;
	root->rch = temp->lch;
	temp->lch = root;

	//更新树的高度
	//只有被操作的两个节点(root,temp=root->rch)的高度会改变
	//由于新树中temp为根,root为子节点,故先更新root的高度
	Update(root);
	Update(temp);
	return temp;
}
AVL* RotateRight(AVL* root) {//右旋,根的左儿子变为根,根变为右儿子
	AVL* temp = root->lch;
	root->lch = temp->rch;
	temp->rch = root;
	//更新树的高度
	//只有被操作的两个节点(root,temp=root->rch)的高度会改变
	//由于新树中temp为根,root为子节点,故先更新root的高度
	Update(root);
	Update(temp);
	return temp;
}
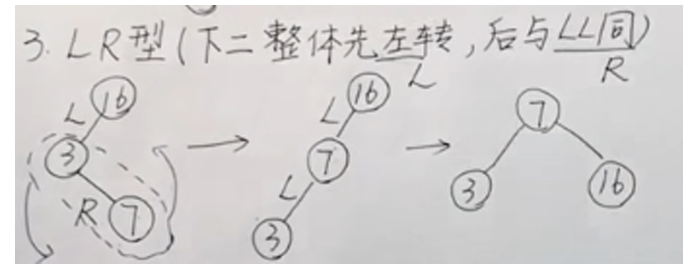
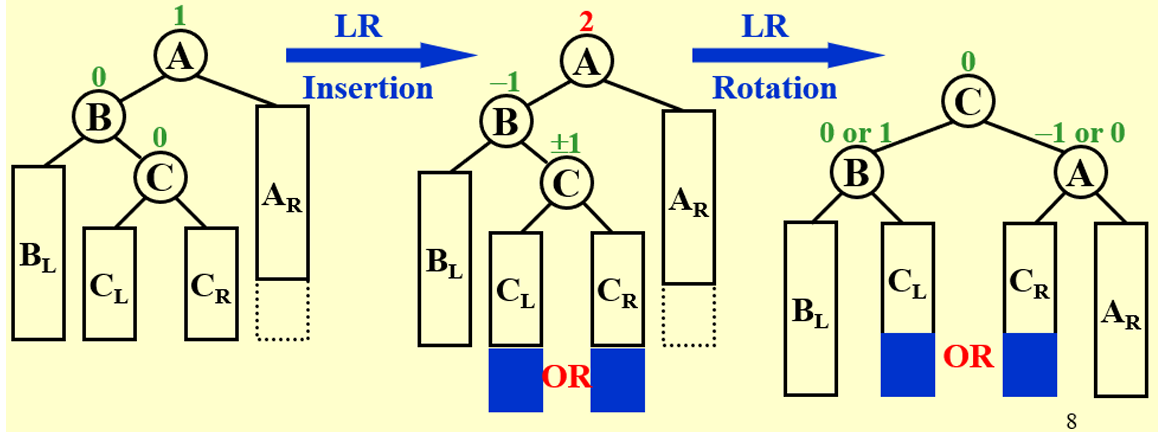
AVL* RotateLeftRight(AVL* root) {//左右旋,先左旋左儿子,再右旋根
	root->lch = RotateLeft(root->lch);
	root = RotateRight(root);
	return root;
}
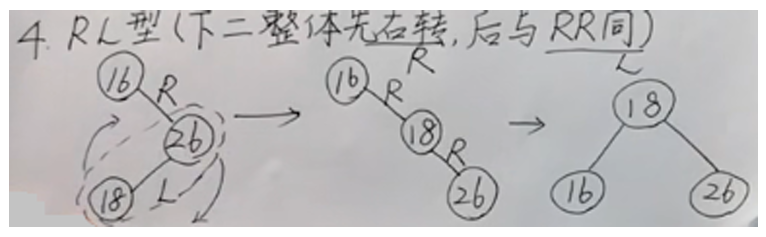
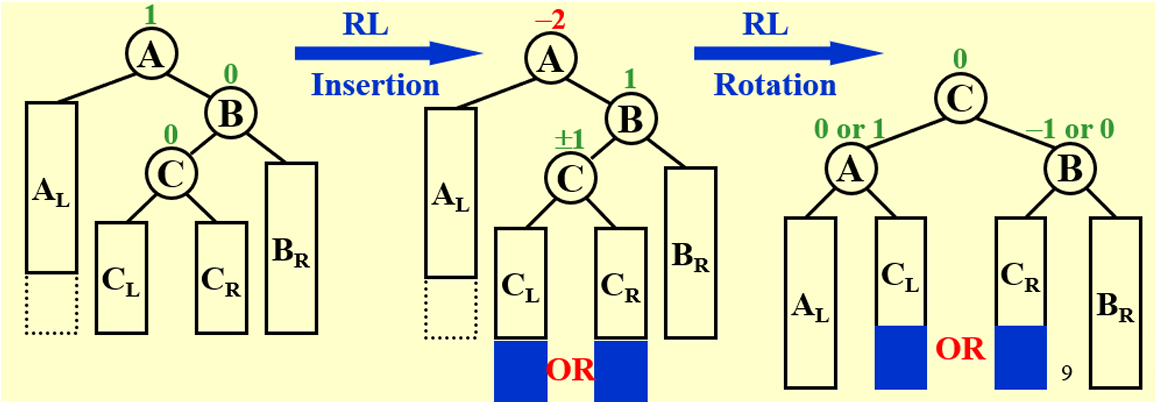
AVL* RotateRightLeft(AVL* root) {//右左旋,先右旋右儿子,再左旋根
	root->rch = RotateRight(root->rch);
	root = RotateLeft(root);
	return root;
}
AVL* Insert(AVL* root, int data) {//插入data
	if (root == NULL) {
		root = new AVL();
		root->data = data;
		root->lch = NULL;
		root->rch = NULL;
		root->height = 1;
		root->sum = 1;
		root->size = 1;
		return root;
	}
	else if (data == root->data) {
		root->sum++;
		root->size++;
		return root;
	}
	else if (data < root->data) {//data插入到左子树
		root->lch = Insert(root->lch, data);
		Update(root);
		//因为插入在左子树,因此只可能是左子树的深
		if (root != NULL && GetBalance(root) == 2) {//左子树过深
			if (GetBalance(root->lch) == -1) {//LR型
				root = RotateLeftRight(root);
			}
			else {//LL型
				root = RotateRight(root);
			}
		}
	}
	else {
		root->rch = Insert(root->rch, data);
		Update(root);
		//因为插入在右子树,因此只可能是右子树深
		if (root != NULL && GetBalance(root) == -2) {//右子树过深
			if (GetBalance(root->rch) == 1) {//RL型
				root = RotateRightLeft(root);
			}
			else {//RR型
				root = RotateLeft(root);
			}
		}
	}
	return root;
}

AVL* Delte(AVL* root, int key, int delta) {
	if (root == NULL)return NULL;	
	if (key < root->data) {
		root->lch = Delte(root->lch, key, delta);
		Update(root);
		//因为删除的是左子树中的节点,因此只可能是左子树的浅
		if (root != NULL && GetBalance(root) == -2) {//右子树过深
			if (GetBalance(root->rch) == 1) {//RL型
				root = RotateRightLeft(root);
			}
			else {//RR型
				root = RotateLeft(root);
			}
		}
		return root;
	}
	else if (key > root->data) {
		root->rch = Delte(root->rch, key, delta);
		Update(root);
		//因为删除的是右子树中的节点,因此只可能是右子树浅
		if (root != NULL && GetBalance(root) == 2) {//左子树过深
			if (GetBalance(root->lch) == -1) {//LR型
				root = RotateLeftRight(root);
			}
			else {//LL型
				root = RotateRight(root);
			}
		}
		return root;
	}
	else {//找到该值,进行删除操作
		root->sum -= delta;
		root->size -= delta;
		if (root->sum > 0)return root;
		if (root->lch != NULL && root->rch != NULL) {//不是叶节点
			AVL* temp = FindNext(root, key);//找到比key大的最小的数
			root->data = temp->data;
			root->sum = temp->sum;//将后继节点替换当前节点
			root->rch = Delte(root->rch, temp->data, Inf);
			Update(root);
			//因为删除的是右子树中的节点,因此只可能是右子树的深度-1
			if (root != NULL && GetBalance(root) == 2) {//左子树过深
				if (GetBalance(root->lch) == -1) {//LR型
					root = RotateLeftRight(root);
				}
				else {//LL型
					root = RotateRight(root);
				}
			}
			return root;
		}
		else {//删除的点的度数为0/1
			AVL* temp = root;
			if (root->lch == NULL)root = root->rch;
			else if (root->rch == NULL)root = root->lch;
			delete temp;
			Update(root);
			return root;
		}
	}
}
int GetRank(AVL* root, int key) {
	if (root == NULL)return 0;
	if (key == root->data)//key == 当前节点的值
		return GetSize(root->lch) + 1;
	else if (key > root->data)//key > 当前节点的值 ==> 在右子树里面
		return GetSize(root->lch) + root->sum + GetRank(root->rch, key);
	else //key < 当前节点的值 ==> 在左子树里面 
		return GetRank(root->lch, key);
}
AVL* FindByRank(AVL* root, int rank) {
	if (rank > GetSize(root->lch) + root->sum)//比左子树+自己大 ==> 在右子树里
		return FindByRank(root->rch, rank - GetSize(root->lch) - root->sum);
	else if (rank > GetSize(root->lch))//比左子树大 ==> 就是自己
		return root;
	else//比左子树小 ==> 在左子树里
		return FindByRank(root->lch, rank);
}
AVL* FindPre(AVL* root, int key) {//找比key小的最大的数
	AVL* ans = NULL;
	while (root != NULL) {
		if (key <= root->data) {//root>key,在左子树 
			root = root->lch;
		}
		else {//root<key,在右子树 
			if (ans == NULL || ans->data < root->data)ans = root;
			root = root->rch;
		}
	}
	return ans;
}
AVL* FindNext(AVL* root, int key) {//找比key大的最小的数
	AVL* ans = NULL;
	while (root != NULL) {
		if (key < root->data) {//root>key,在左子树 
			if (ans == NULL || ans->data > root->data)ans = root;
			root = root->lch;
		}
		else {//root<key,在右子树 
			root = root->rch;
		}
	}
	return ans;
}