ADS02:平衡树(含实现)--B+树
一、定义
\[ Depth(M,N)=O(\lceil log_{\lceil \frac{M}{2} \rceil} N \rceil) \]
m阶B+树满足:
- 根节点有2 ~ m个子节点/0个子节点
- 所有非根非叶节点,有\(\lceil \frac{m}{2} \rceil\) ~ m个子节点
- 所有叶节点的深度相同
- 非叶节点不保存数据,而是保存索引
- 索引保存对应子节点的最小值
- 若有x个子节点,则有x-1个索引
B树的内部节点保存数据,而B+树不保存
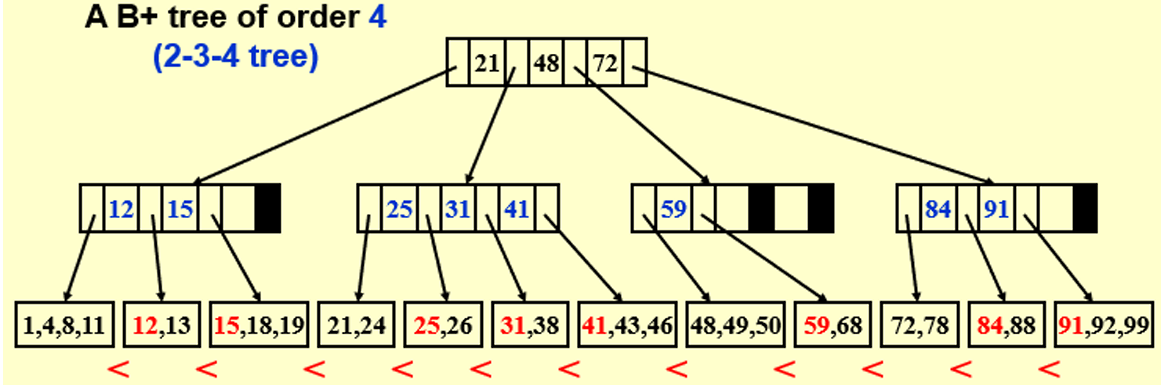
二、查找
\[ T_{Find}(M,N)=O(log\ N) \]
如果有n个子节点,则对应n-1个key值
- 若x < key[0],则沿指针child[0]所指的子树继续查找
- 若key[i] <= x < key[i+1],则沿指针child[i+1]所指的子树继续查找
- 若x >= key[n-1],则沿着指针child[n]所指的子树继续查找
- 直到找到叶节点为止
三、插入
\[ T(M,N)=O(\frac{M}{log\ M}log\ N) \]
3.1 找到关键字x的插入节点
注意:B+树的插入节点一定是叶节点
3.2 插入关键字x
- 插入节点有空位置(即原关键字个数n < m) ==> 直接把关键字x有序插入到该节点的合适位置
- 插入节点没有空位置(即原关键字个数n = m) ==> 分裂
- 将x插入,此时该叶节点有m+1个
- 将该叶节点从中间分裂,变为两个叶节点
- 在父节点中建立对应的索引
例1:父节点有位置
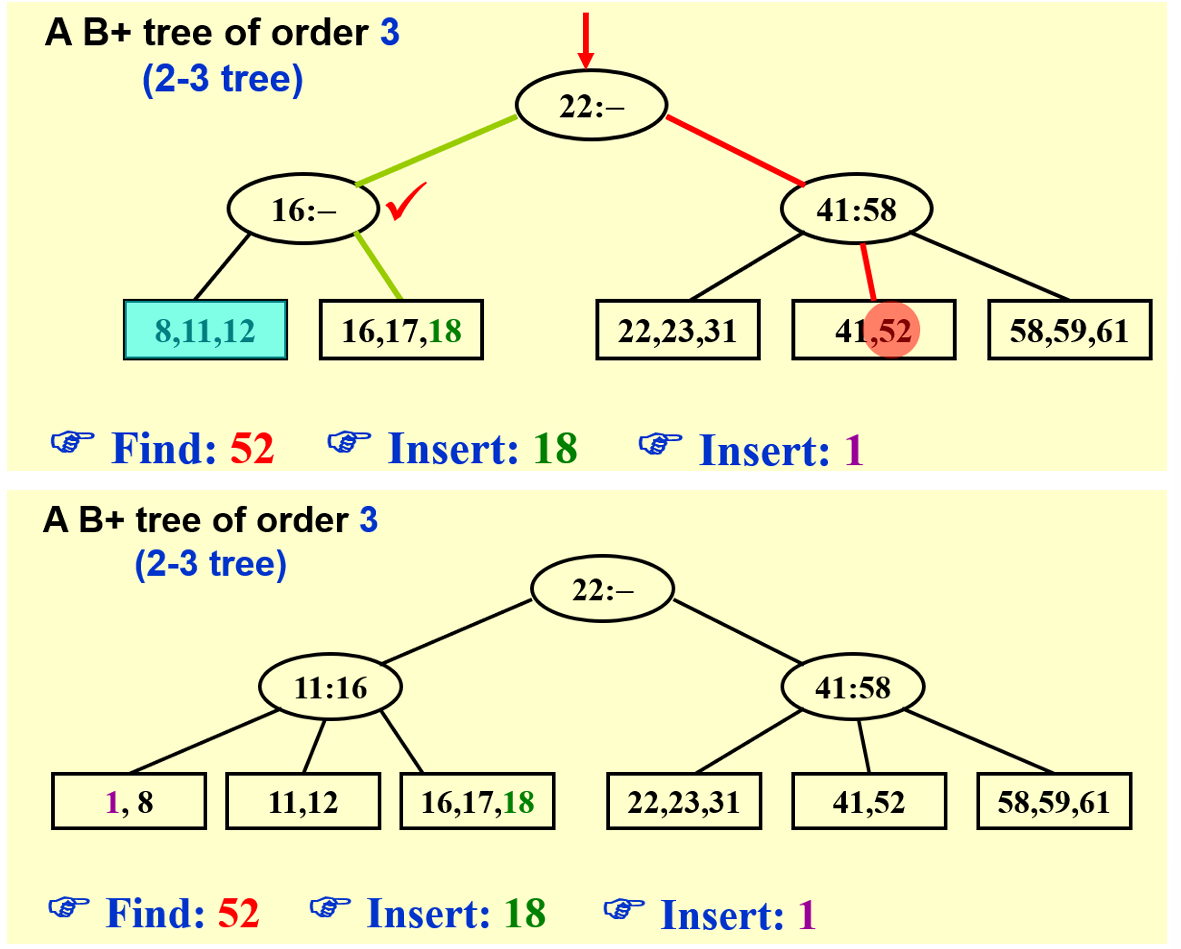
例2:父节点没有位置
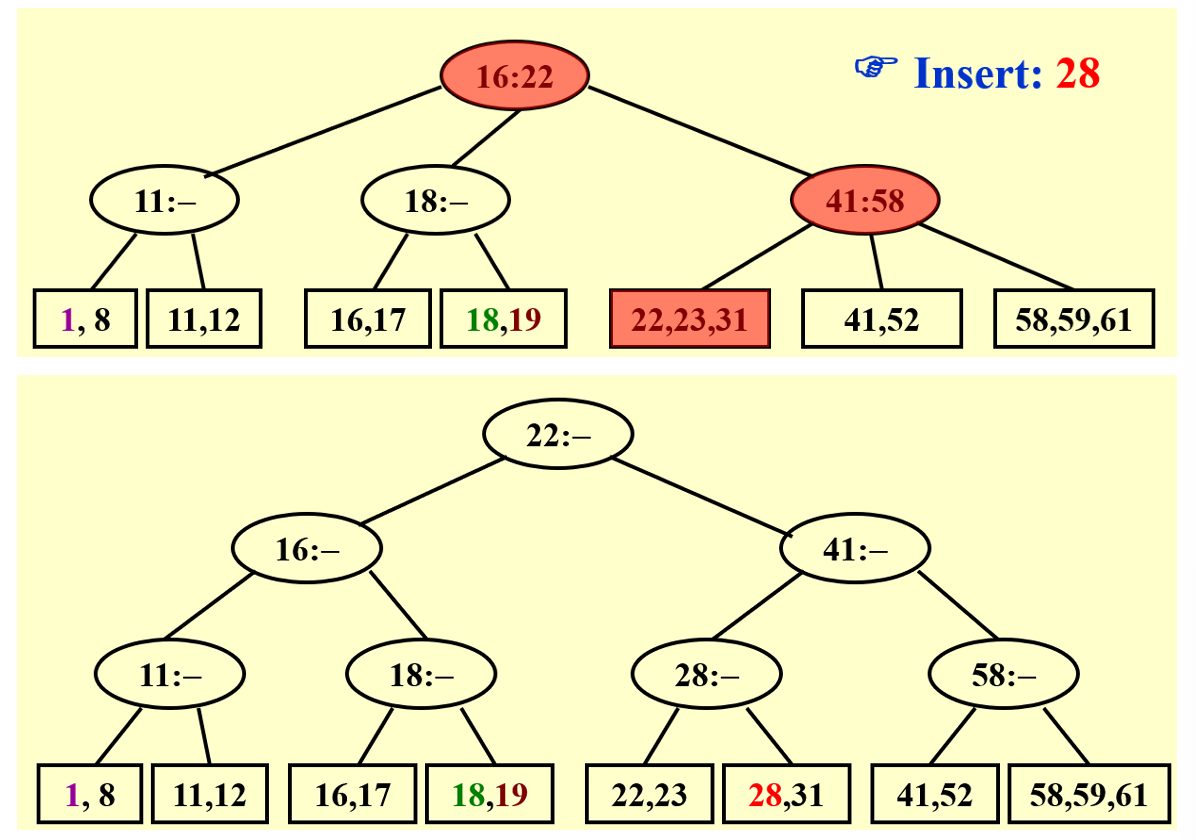
四、删除
4.1 找到关键字x所在的叶节点
4.2 删除关键字x
- 叶节点的关键字个数 > ceiling(m/2) ==> 直接删除
- 叶节点的关键字个数 = ceiling(m/2) ==>
删除后,合并兄弟节点
- 将x删除,此时该叶节点的关键字个数不足
- 将该叶节点与兄弟节点合并
- 删除父节点中的对应索引
例:删除父节点中的索引后,父节点个数不足
五、作业题
A B+ tree of order 3 with 21 numbers has at most __ nodes of degree 3.
- 题目意思:一个3阶B+树,有21个数字,最多有__个节点的度为3
- 答案:4
- 解答:3阶B+树,每个内点的度为2 or 3,可以是如下类型
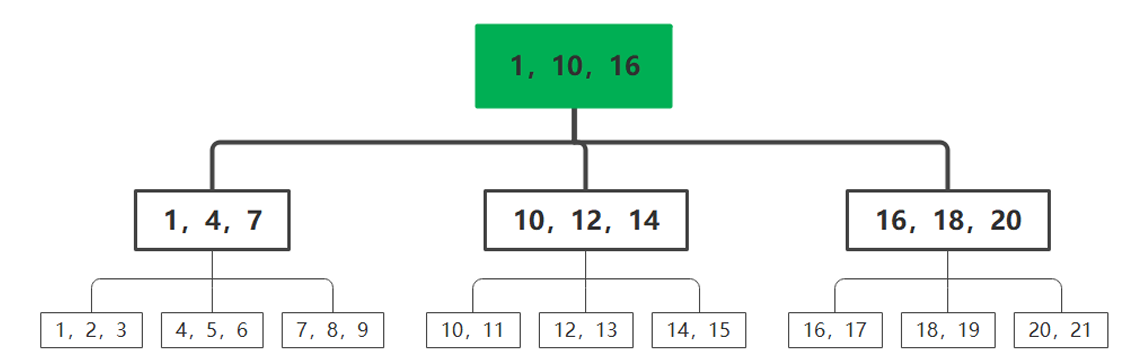
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 华风夏韵!
评论