一、定义

1.1 平衡树的定义

树的深度为O(log(n))

1.2 颜色定义：

每一个节点均为Red/Black
根是Black的
叶节点是Black的
- 这里的叶节点指的是为空的叶节点
如果一个节点是Red的，那么他的子节点是Black的
- 即：两个Red节点不能相连
对于任意节点，该节点到后代叶节点的所有简单路径包含的Black节点个数相同

二、性质

bh(x)：表示从x到叶节点的任意一条简单路径，包含的Black节点个数
引理：一个有n个内部节点的红黑树，高度最多为2 log(n+1)

证明(数学归纳法)：

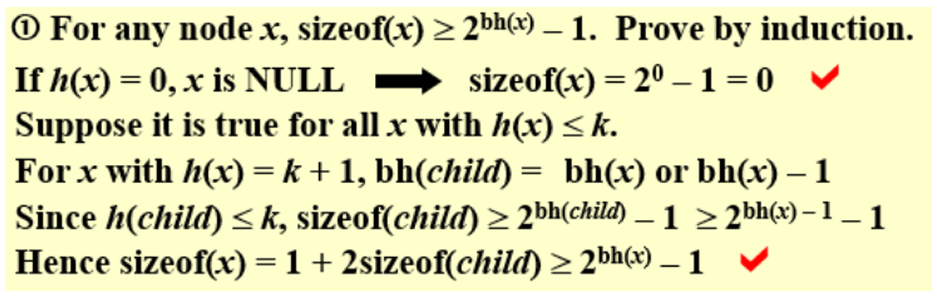
三、插入

3.1 插入节点

将红黑树当作一颗BST，将节点插入

3.2 着色为Red

此时，新插入的点只可能违背定义(4)：

如果一个节点是Red的，那么他的子节点是Black的

3.3 调整为红黑树

通过一系列旋转/着色操作，使之重新成为一颗红黑树

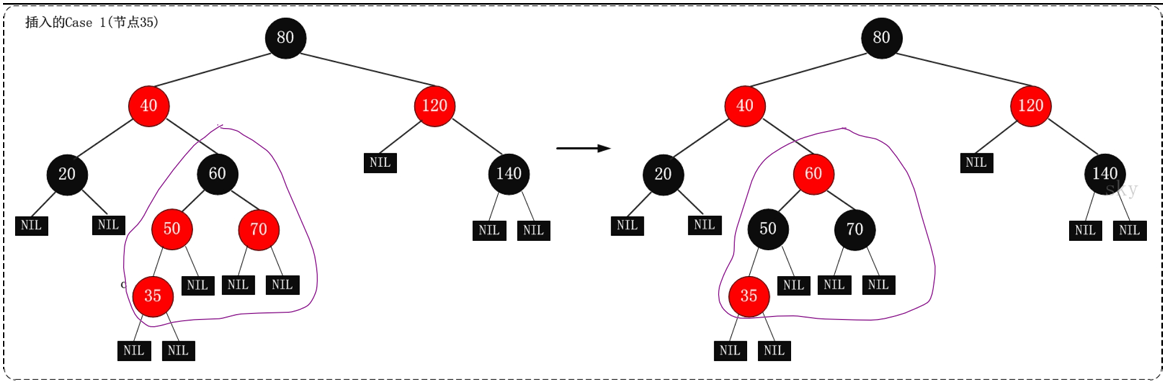
3.3.1 情况1：父节点为Red，叔叔节点为Red

==> 父辈设为Black，祖先设为Red

==> 矛盾上移

将 “父节点” 设为Black
将 “叔叔节点” 设为Black
将 “祖父节点” 设为Red
将 “祖父节点” 设为 “当前节点” ，之后继续对 “当前节点” 进行操作

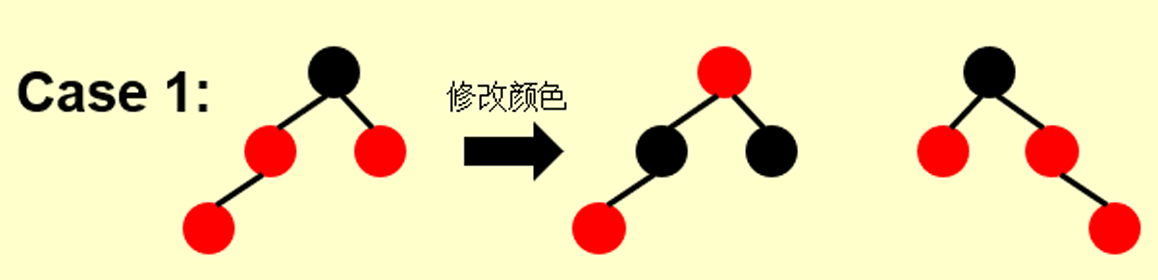
3.3.2 情况2：父节点为Red，叔叔节点为Black，当前节点为右儿子

==> 左旋父节点

==> 转化为情况3

将 “父节点” 作为 “新的当前节点”
以 “新的当前节点” 为支点进行左旋
从而变成了情况3

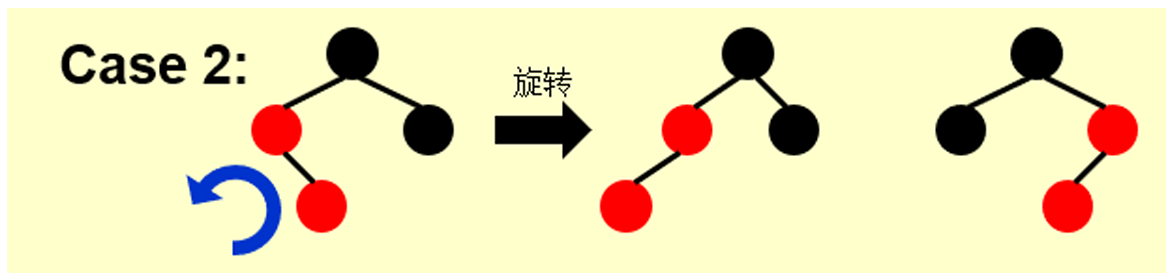
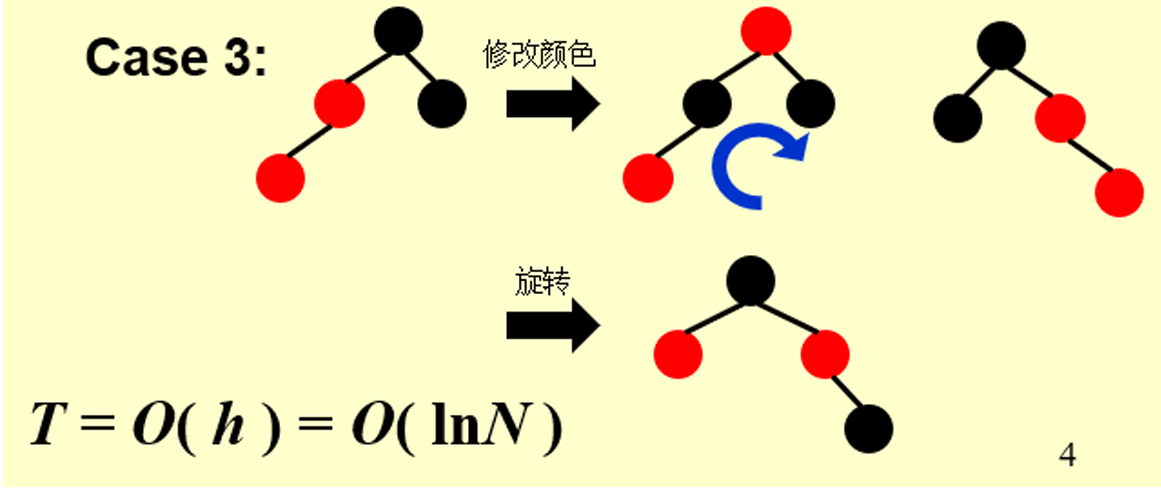
3.3.3 情况3：父节点为Red，叔叔节点为Black，当前节点为左儿子

==> 父节点设为Black，祖父设为Red

==> 右旋祖父，矛盾解除

将 “父节点” 设为Black
将 “祖父节点” 设为Red
以 “祖父节点” 为支点进行右旋

四、删除

4.1 删除节点

将红黑树当作一颗BST，将节点删除

叶节点：直接删除
只有1个儿子：儿子直接顶替
有2个儿子：
- 找到 后继节点
- 把 后继节点 的内容复制给 该节点（不复制Color）
- 删除 后继节点

4.2 调整为红黑树(x为左儿子)

如果删除的节点是Red，直接删除即可
如果删除的节点是Black，分成4种情况

设删除后取代原节点的点为x(为黑色)，其兄弟节点为W，父节点为A

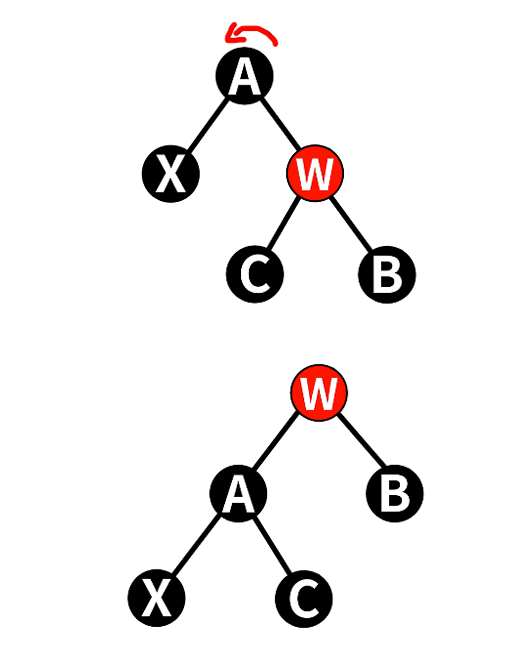
4.2.1 情况1：w为红色

==> 左旋A，交换A&w颜色

==> 转化为w为黑的情况

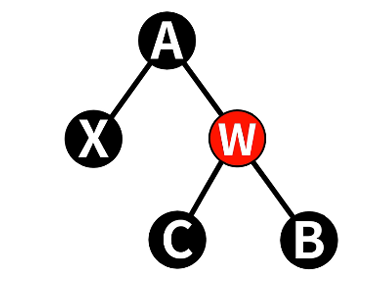
将w和A交换颜色
对x的父节点进行左旋

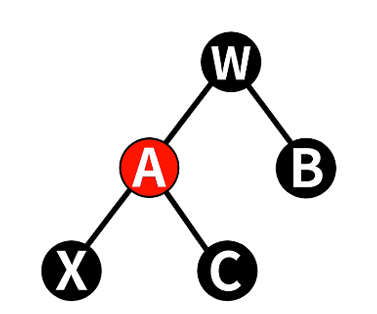
将x的新兄弟设为w，转换为后三种情况的任意一种

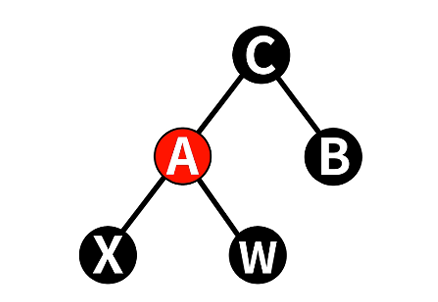
4.2.2 情况2：w为黑色，且w的子节点为黑色

==> w设为红

==> 左右子树黑高均-1，矛盾上移

==> 结束时将根设为黑，整颗子树黑高不变

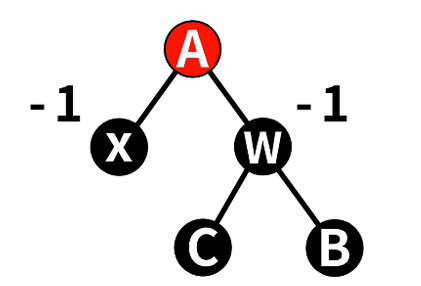
将w变为Red，这样另一颗子树黑高-1

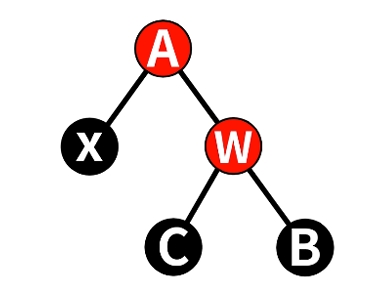
将A点视为新的x，继续进行修复操作，直到x为根节点/为红色时退出。

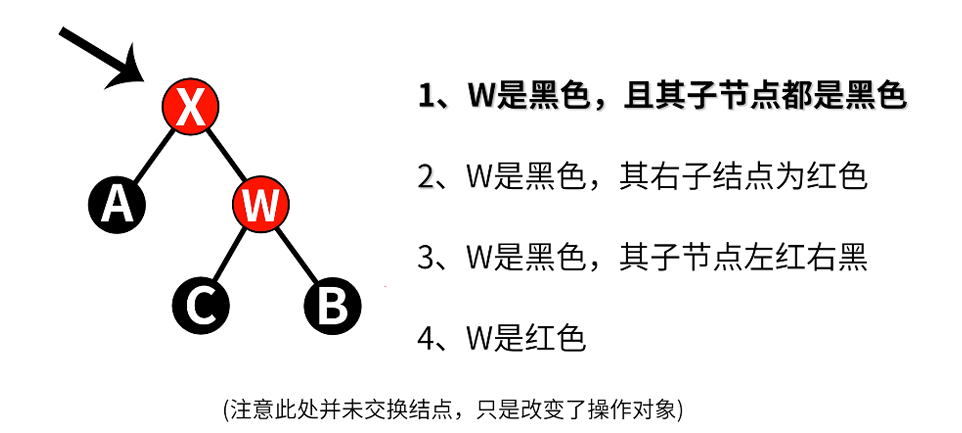
退出后，将x设为黑色，保证不会出现相邻红节点

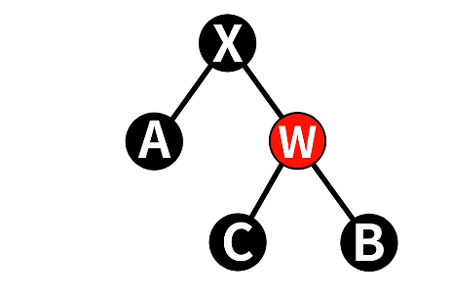
4.2.3 情况3：w为黑色，且w的子节点左红，右黑

==> 右旋w，交换w&C颜色

==> 转化为情况4

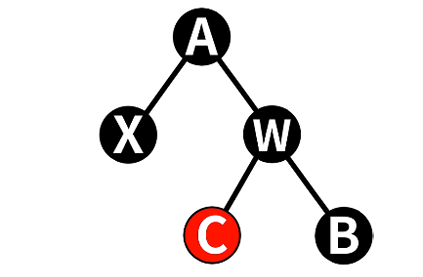
令w为Red，左节点为Black
对w进行右旋
转变为情况4：右子节点为红

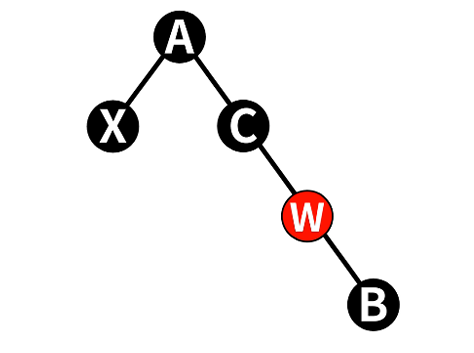
4.2.4 情况4：w为黑色，且w的右红，左任意

==> w为A色，A&B设为黑，左旋A

==> 左右子树黑高不变

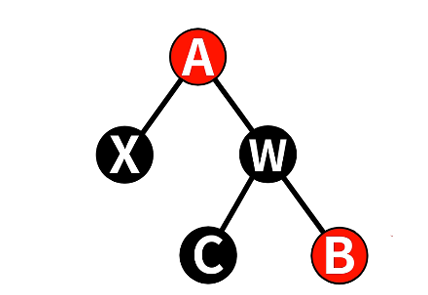
(1)将w变为和x的父节点A同色

w.color = x.prt.color;

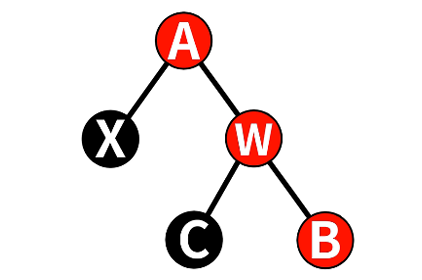
(2)将w的父节点A、w的右子节点B设为Black

x.prt.color = BLACK;
w.rch.color = BLACK;

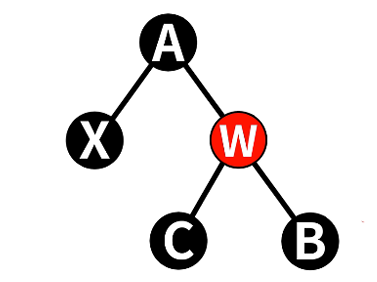
(3)把x的父节点A进行左旋

RotateLeft(x->prt);

4.2 删除的时间复杂度

重新着色的时间：最坏情况是O(log n)，平均情况是O(1)
旋转的时间：最多3次

五、作业题

A. 11是6的父节点，14是红节点
B. 8是15的父节点，7是黑节点
C. 11是15的父节点，一共有2个红节点
D. 8是15的父节点，一共有2个红节点

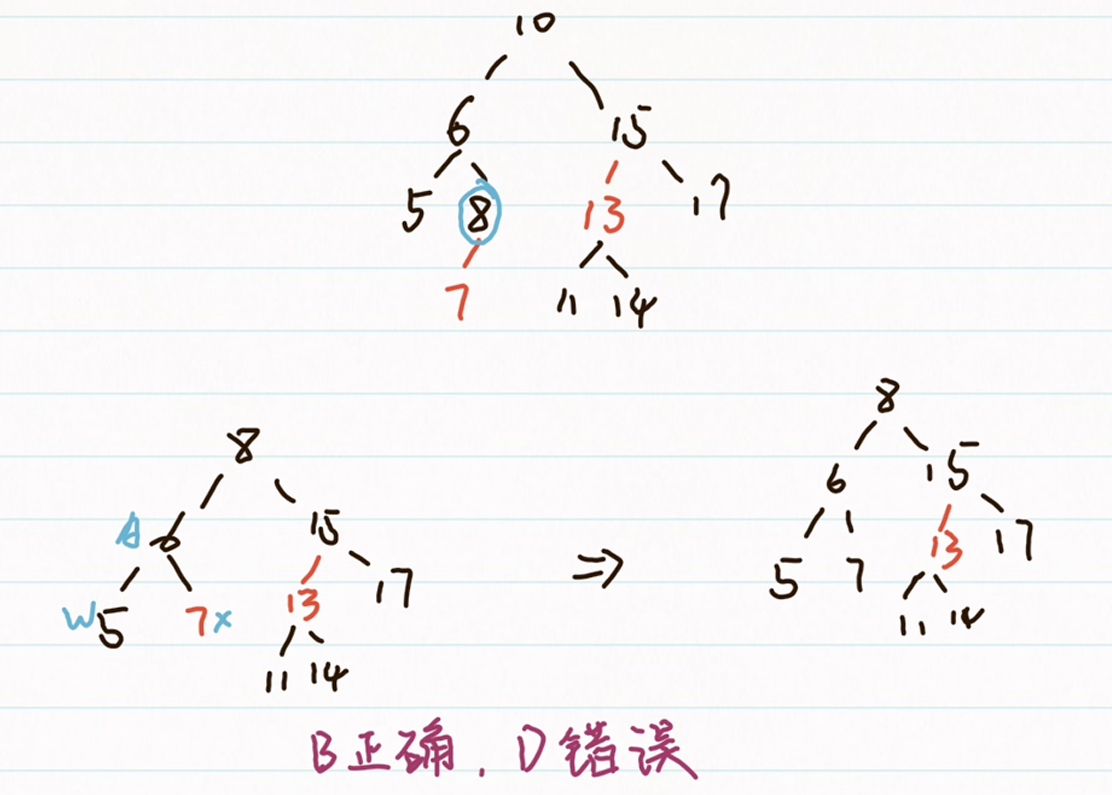
删除之后10之后，有两种情况

用8顶替10

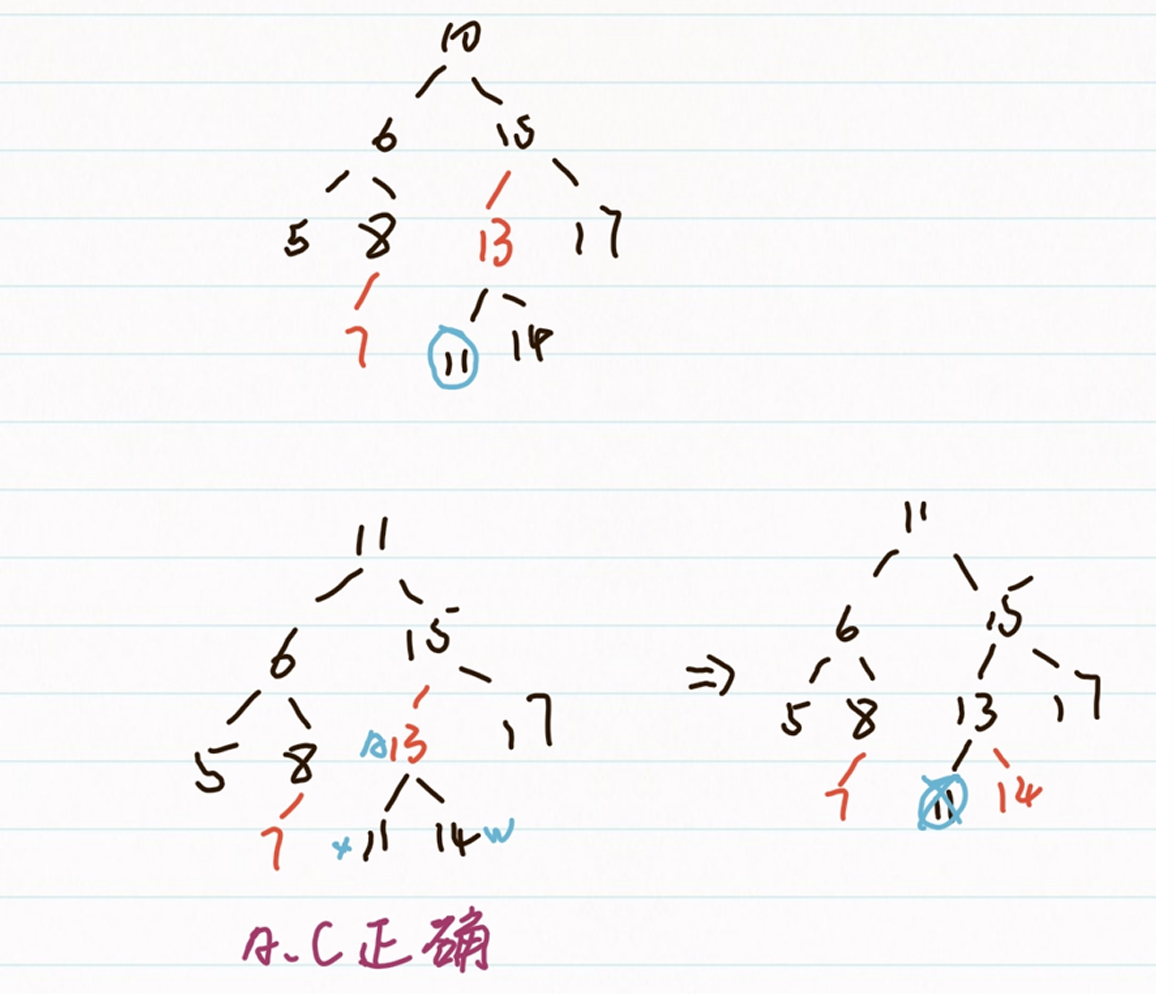
用11顶替10