合并方法：

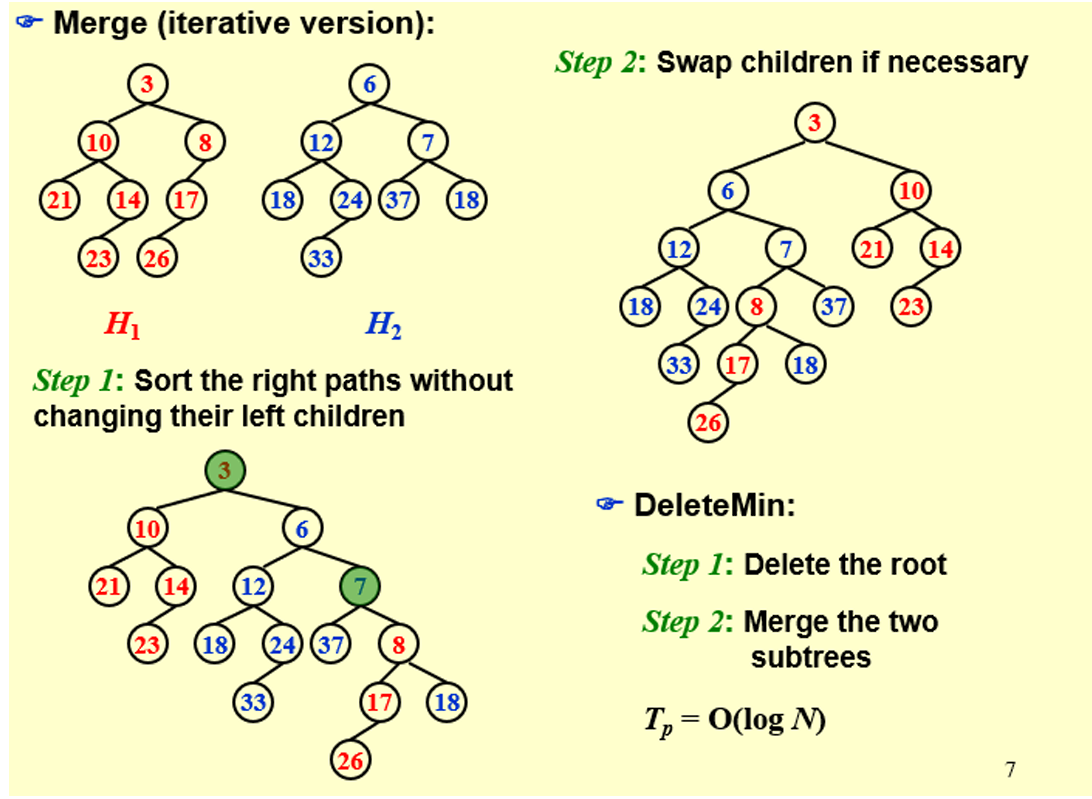
  1. 先将\(H_2\)合并到\(H_1\)的右子树中，记录每一步被当作根的节点
  2. 从最后一个被当作根的节点开始，向上回溯
    1. 如果是左偏堆，则根据NPL判断是否需要交换左右子树
    2. 如果是斜堆，则始终交换左右子树

左偏堆 Leftist Heap

一、基础概念

Full Binary Tree：每个节点都有0/2个儿子

Complete Binary Tree：除了最后一层，每一层都满了

堆Heap：

  • 任意一条从根到叶节点的路径，是有序的
  • 结构性质、顺序性质
  • 在O(n)的时间内，可以将两个堆合并

二、性质

空路径长度null path length：Npl(X)：

  • 从节点x开始到叶节点的最短的路径长度
  • Npl(x) = min{Npl(c) c为x的子节点} + 1

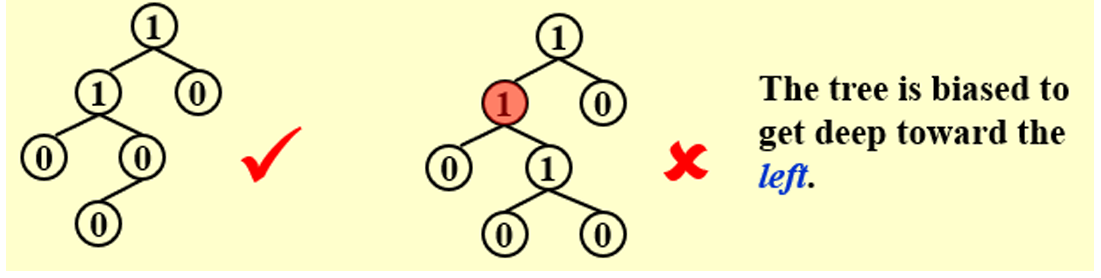
左偏堆Leftist Heap：

  • 满足顺序性质，但是不满足结构性质(左子树size>右子树size)
  • 对于左偏堆中的每个节点x，左子节点的空路径长度>=右子节点

节点上的数字，表示当前节点的Npl值

image-20240416194844582

定理：如果左偏堆的右路径有r个节点，那么其至少有\(2^r\) - 1个节点 \[ \begin{aligned} 证明：&1.当r=1时，显然成立 \\ &2.当r>1时，假设k=r-1时，假设成立\\ &设当前节点为a，左子节点为b，右子节点为c\\ &对于此时的根节点，因为右路径为r，因此其NPL(c)\geq r-1\\ &由于左偏堆的性质，此时左子树满足NPL(b)\geq r-1\\ &由假设得，左右子树的节点个数均\geq 2^{r-1}-1 \\ &因此该子树的节点个数\geq 2^r-1 \end{aligned} \]

三、结构体

struct LHeap{
    int element;
    LHeap* Left;
    LHeap* Right;
    int NPL;
};

四、合并

LHeap* Merge(LHeap* H1, LHeap*H2){
    if(H1 == NULL) return H2;
    if(H2 == NULL) return H1;
    if(H1->element < H2->element) return Merge1(H1,H2);
    else return Merge1(H2,H1);
}
LHeap* Merge1(LHeap* H1, LHeap* H2 ){ 
//H1的根节点的值 < H2的根节点的值
	if (H1->Left == NULL){//H1为单个节点
		H1->Left = H2;//将H2作为H1的左子树,因为要满足左边的NPL大
    }else {
		H1->Right = Merge(H1->Right,H2);//将H2与H1的右子树合并
		if (H1->Left->Npl < H1->Right->Npl)
			SwapChildren(H1);//如果左子树的NPL小,则转换左右子树
		H1->Npl = H1->Right->Npl + 1;//更新根节点的NPL值
	}
	return H1;
}

image-20240416194950545

斜堆 Skew Heap

一、合并

1.1 原理

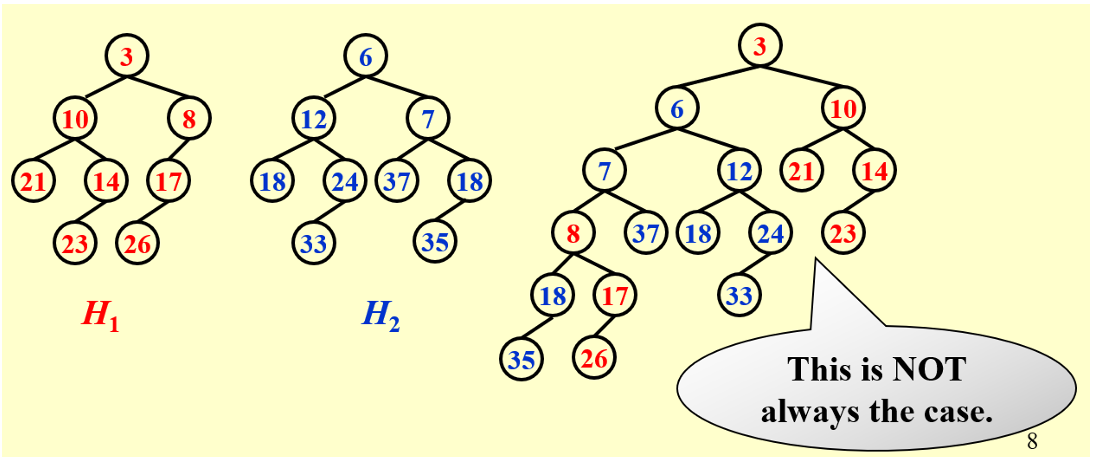
总是交换左右子树，除非右面路径上的最大节点的子树没有被交换

任意M次连续操作，时间最多为O(M log N)，N=N1+N2

image-20240416195348001

image-20240416195402464

1.2 代码

struct Node {
    int data;
    Node* lch, * rch;
    Node() {};
    Node(int x) {
        data = x;
        lch = rch = NULL;
    }
};
Node* root;
void SwapChildren(Node* H) {
    Node* temp = H->lch;
    H->lch = H->rch;
    H->rch = temp;
}
Node* Merge(Node* H1, Node* H2) {
    if (H1 == NULL)return H2;
    if (H2 == NULL)return H1;
    if (H1->data > H2->data) {
        Node* temp = H1;
        H1 = H2;
        H2 = temp;
    }
    if (H1->lch == NULL)//H1是单个节点
        H1->lch = H2;
    else {
        H1->rch = Merge(H1->rch, H2);
        SwapChildren(H1);
    }
}

二、时间复杂度证明

\[ \begin{aligned} 定义：&如果节点p的右子树的后代至少为p的后代数的一半，则p为重节点\\ &注意，p节点的后代数包括p本身\\\\ 引理1:&在H_1、H_2右路径中的重节点，在H_3中变为了轻节点\\ &假设a为重节点,a要和b合并\\ &(1)a>b,则a的右子树与b合并,并且作为a的左子树,\\ &合并后左子树比右子树大,a变为轻节点\\ &(2)a<b,则a与b的右子树合并,设b的右节点为c\\ &如果a>c,则变为(1)\\ &如果a<c,则变为(2),继续向下处理\\ \\ 引理2:&一棵树,如果其右路径有k个轻节点,则至少有2^k-1个节点\\ &数学归纳法:当前树的节点数\geq 2(2^k-1)+1 \geq 2^{k+1}-1\\ \\ 证明：&设合并前为H_1,H_2，合并后为H_3\\ &\Phi(H_i)=H_i树中，重节点的个数\\ &设一共进行了m次递归,则\\ &\sum_{i=1}^{m} \hat c_i = \sum_{i=1}^{m} c_i +\Phi(H_3)-\Phi(H_1)-\Phi(H_2) \\ &设H_i的右路径中，轻节点有l_i个，重节点有h_i个，则\\ &\sum_{i=1}^{m} c_i \leq l_1 + h_1 + l_2 + h_2 \\ & 令\Delta \Phi=\Phi(H_3)-\Phi(H_1)-\Phi(H_2),由引理1得 \\ &\Delta \Phi \leq l_1 + l_2 - (h_1 + h_2) \\ &\therefore \sum_{i=1}^{m} \hat c_i \leq l_1 + h_1 + l_2 + h_2 + \Delta \Phi \\ &\leq l_1 + h_1 + l_2 + h_2 + l_1 + l_2 - (h_1 + h_2)\\ &=2(l_1 + l_2),由引理2\\ &=O(log\ n_1)+O(log\ n_2) \end{aligned} \]

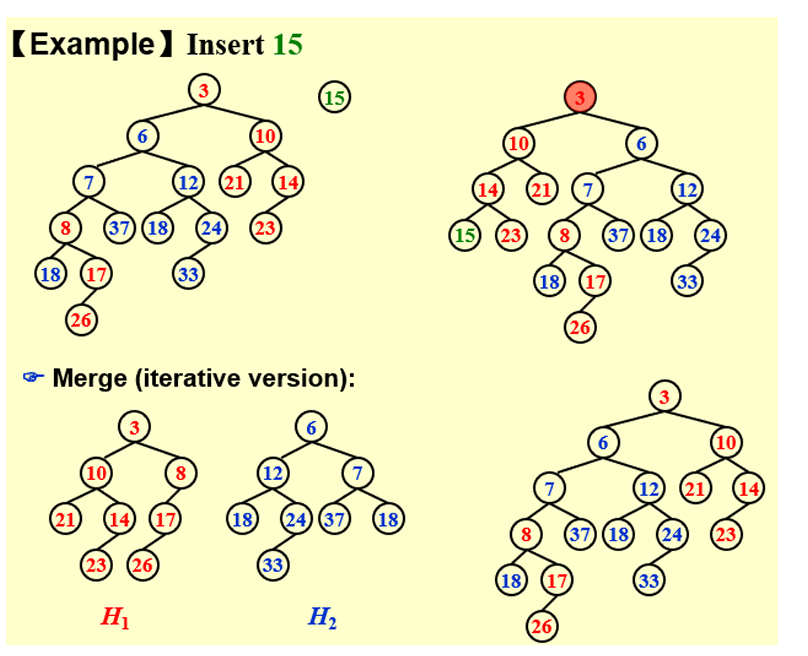
例题

image-20240416195550896

右路径上重点、轻点的个数为O(log N)

斜堆的代码实现

#pragma warning(disable:4996)
#include <cstdio>
#include <queue>
#include <algorithm>
#include <ctime>
using namespace std;
class SkewHeap {
	struct Node {
		int data;
		int size;
		Node* lch, *rch;
		Node() {
			data = 0;
			size = 0;
			lch = rch = NULL;
		}
		Node(int x) {
			data = x;
			size = 1;
			lch = rch = NULL;
		}
		void Update() {
			size = 1;
			if (lch != NULL) size += lch->size;
			if (rch != NULL) size += rch->size;
		}
	};
private:
	static const int maxSize = 100000 + 10;
	Node* root;
	void SwapChildren(Node* H) {
		Node* temp = H->lch;
		H->lch = H->rch;
		H->rch = temp;
	}
	int GetData(Node* u) {
		if (u == NULL)return -1;
		return u->data;
	}
	Node* Merge(Node* H1, Node* H2) {
		if (H1 == NULL)return H2;
		if (H2 == NULL)return H1;
		if (H1->data > H2->data) {
			Node* temp = H1;
			H1 = H2;
			H2 = temp;
		}
		if (H1->lch == NULL)//H1是单个节点
			H1->lch = H2;
		else {
			H1->rch = Merge(H1->rch, H2);
			SwapChildren(H1);
		}
	}
public:
	SkewHeap() {
		root = new Node();
	}
	void reset() {
		root = new Node();
	}
	int size() {
		return root->size;
	}
	void Insert(int x) {
		if (root->size == 0) {
			root->data = x;
			root->size = 1;
			return;
		}
		Node* now = new Node(x);
		root = Merge(root, now);
	}
	int top() {
		return root->data;
	}
	void pop() {
		root = Merge(root->lch, root->rch);
	}
};