一、定义

一个Binomial Queue是一个堆的集合{\({B_k,B_{k-1}...B_0}\)}

  • \(B_k\)一共有\(2^k\)个节点
  • \(B_k\)的根节点有\(k\)个子节点，分别是\(B_0,B_1...B_{k-1}\)
  • \(B_k\)中深度为d的节点个数为\(C_k^d\)

\[ \begin{aligned} &设B_k中深度为x的节点个数为f(k,x),则\\ &\because B_k由两个B_{k-1}的树相连得到,其中一个树的根节点作为新树的根节点\\ &\therefore f(k,x)=f(k-1,x)+f(k-1,x-1)\\ &\therefore f(k,x)=C_k^d \end{aligned} \]

二、操作

2.1 FindMin

找所有根节点中的最小值，时间复杂度为\(O(log\ N)\)

也可以实时维护一个最小值，时间复杂度为\(O(1)\)

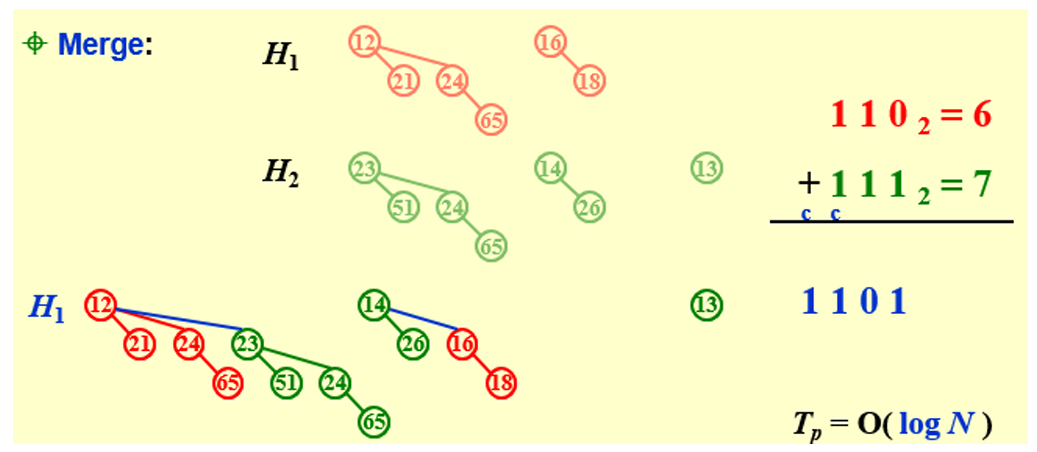
2.2 Merge

类似于二进制加法，将对应的\(B_i\)树合并

image-20240416195858020

2.3 Insert

进行m次合并，每一次是将一个树与一个节点合并

image-20240416195952608

2.4 Delete

  • 找到最小值
  • 将最小值删除，此时最小值所在的\(B_i\)分裂成一个新的Binomial Queue
  • 将新的Binomial Queue与原有的Binomial Queue合并

image-20240416200011300

2.4 Decrease Key

假设x在\(B_i\)中，变换x的数值

三、PPT中的实现

使用left-child-next-sibling将多叉树转化为二叉树，此时根节点必然只有左儿子，没有右儿子

3.1 结构体

typedef struct BinNode *Position;
typedef struct Collection *BinQueue;
typedef struct BinNode *BinTree; 
// missing from p.176

struct BinNode { 
	ElementType	    Element;
	Position	    LeftChild;
	Position 	    NextSibling;
};

struct Collection { 
	int	CurrentSize;  //total number of nodes
	BinTree	TheTrees[ MaxTrees ];
} ;

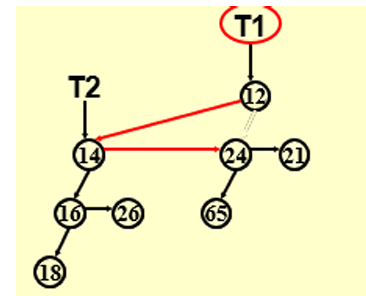
3.2 二叉树合并

BinTree CombineTrees( BinTree T1, BinTree T2 ){  //merge equal-sized T1 and T2 
	//attach the larger one to the smaller one 
    if ( T1->Element > T2->Element )
		return CombineTrees( T2, T1 );
	//insert T2 to the front of the children list of T1
	T2->NextSibling = T1->LeftChild;
	T1->LeftChild = T2;
	return T1;
}

image-20240416200124758

3.3 Merge

BinQueue  Merge( BinQueue H1, BinQueue H2 ){	
    BinTree T1, T2, Carry = NULL; 	
	int i, j;
	if ( H1->CurrentSize + H2-> CurrentSize > Capacity )  ErrorMessage();
	H1->CurrentSize += H2-> CurrentSize;
	for ( i=0, j=1; j<= H1->CurrentSize; i++, j*=2 ) {
	    T1 = H1->TheTrees[i]; T2 = H2->TheTrees[i]; /*current trees */
	    switch( 4*!!Carry + 2*!!T2 + !!T1 ) { 
		case 0: // 000
	 	case 1: // 001 
                break;	
		case 2: // 010 
                H1->TheTrees[i] = T2; 
                H2->TheTrees[i] = NULL; 
                break;
		case 4: // 100 
                H1->TheTrees[i] = Carry; 
                Carry = NULL; 
                break;
		case 3: // 011 
                Carry = CombineTrees( T1, T2 );
                H1->TheTrees[i] = H2->TheTrees[i] = NULL; 
                break;
		case 5: // 101 
                Carry = CombineTrees( T1, Carry );
                H1->TheTrees[i] = NULL; 
                break;
		case 6: // 110 
                Carry = CombineTrees( T2, Carry );
                H2->TheTrees[i] = NULL; 
                break;
		case 7: // 111 
                H1->TheTrees[i] = Carry; 
                Carry = CombineTrees( T1, T2 ); 
                H2->TheTrees[i] = NULL; 
                break;
	    }
	}
	return H1;
}

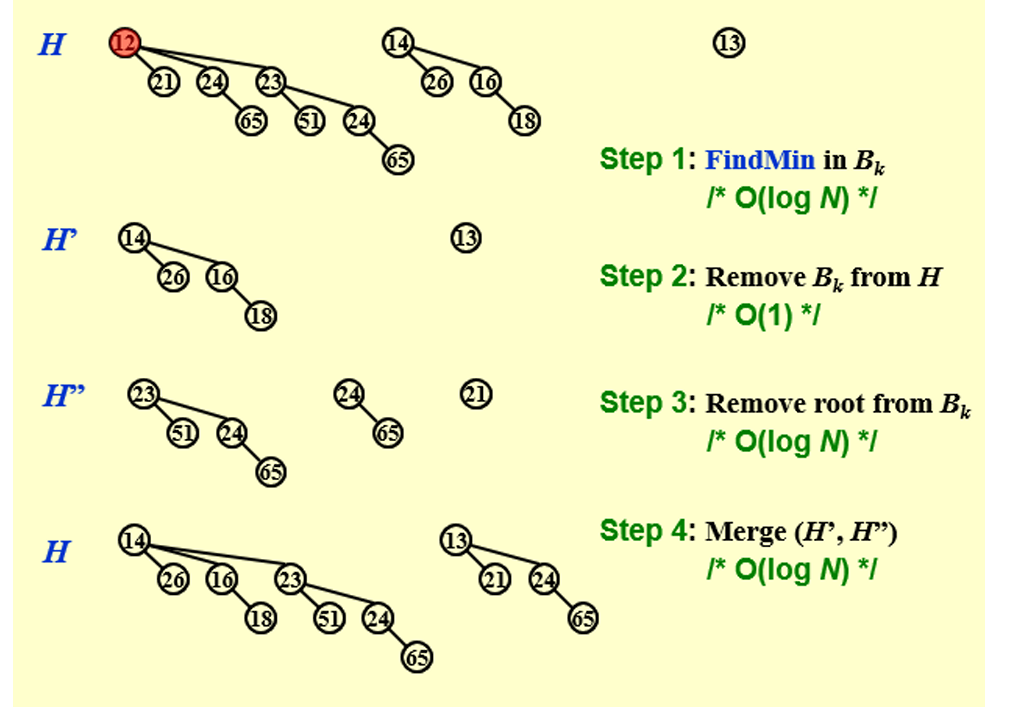
3.4 DeleteMin

注意：建立新的\(H''\)的时候，\(j\)从\(Ind-1 \rightarrow 0\)

ElementType  DeleteMin( BinQueue H ){	
    BinQueue DeletedQueue; 
	Position DeletedTree, OldRoot;
	ElementType MinItem = Infinity;  
    // the minimum item to be returned 
	int i, j, MinTree; 
    // MinTree is the index of the tree with the minimum item 

	if ( IsEmpty( H ) )  {  
        PrintErrorMessage();  
        return –Infinity; 
    }

	for ( i = 0; i < MaxTrees; i++) {  
        // Step 1: find the minimum item 
	    if( H->TheTrees[i] && H->TheTrees[i]->Element < MinItem ) { 
			MinItem = H->TheTrees[i]->Element;  
            MinTree = i;    
        }
	}
	DeletedTree = H->TheTrees[ MinTree ];  
	H->TheTrees[ MinTree ] = NULL;   
    // Step 2: remove the MinTree from H => H’  
	OldRoot = DeletedTree; 
    // Step 3.1: remove the root 
	DeletedTree = DeletedTree->LeftChild;   free(OldRoot);
	DeletedQueue = Initialize();   
    // Step 3.2: create H”
	DeletedQueue->CurrentSize = ( 1<<MinTree ) - 1;  
    // 2MinTree – 1
	for ( j = MinTree - 1; j >= 0; j --) {  
	    DeletedQueue->TheTrees[j] = DeletedTree;
	    DeletedTree = DeletedTree->NextSibling;
	    DeletedQueue->TheTrees[j]->NextSibling = NULL;
	} 
	H->CurrentSize  -= DeletedQueue->CurrentSize + 1;
	H = Merge( H, DeletedQueue );
    // Step 4: merge H’ and H”
	return MinItem;
}

四、连续插入n个点的时间复杂度证明

4.1 Aggregation综合分析

设n为当前binomial queue的大小，当我们插入一个新的节点时，消耗的时间是n的二进制表示中，结尾的1的个数

因此，n次插入所消费的时间为1~n中所有数字的二进制表示中，结尾的1的个数之和，而该数值为\(1*\frac{1}{2}+2*\frac{1}{2^2}+3*\frac{1}{2^3}=\sum_{i=1}^n \frac{i}{2^i}\leq 2\)

因此，总的时间消耗为\({n}*\sum_{i=1}^n \frac{i}{2^i}\leq 2N\)

4.2 Potential潜在分析

设合并两个同样大小的二叉树所需的时间为O(1)

设\(\Phi_i\)表示：第i次合并后，剩余的树的个数，则\(\Phi_0=0\)

设\(C_i\)表示：第i次合并的实际消耗时间，即1+被合并的树的个数

设\(\hat C_i\)表示：第i次合并的均摊消耗时间

则，\(C_i+(\Phi_i-\Phi_{i-1})=2\)

因此，\(\sum_{i=1}^{N}C_i + \Phi_N - \Phi_0=2N\)

==> \(\sum_{i=1}^{N}C_i= 2N- \Phi_N\leq 2N=O(N)\)

\(T_{worst}=O(log\ N)\)，但是\(T_{amortized}=2\)

五、总代码

#pragma warning(disable:4996)
#include<cstdio>
#include<cstring>
#include<ctime>
#include<algorithm>
using namespace std;
class BinomialQueue {
	static const int maxSize = 100000 + 10;//节点的最大数量
	static const int maxTrees = 30;//每个BinQueue中包含的最多的BinTree数目
	static const int INTMIN = -2147483647, INTMAX = 2147483647;
	//BinomialQueue每一位的二叉堆
	struct BinNode {
		int element;
		BinNode* LeftChild;
		BinNode* NextSibling;
		BinNode() {
			element = 0;
			LeftChild = NextSibling = NULL;
		}
		BinNode(int x) {
			element = x;
			LeftChild = NextSibling = NULL;
		}
	};
	typedef BinNode* BinTree;

	//BinomialQueue本体
	struct Collection {
		int CurrentTree;
		//描述当前的BinTree的有哪些
		//其二进制位数为1的位在Trees数组中有对应的树
		BinTree Trees[maxTrees];
		Collection() {
			CurrentTree = 0;
			for (int i = 0; i < maxTrees; i++)
				Trees[i] = NULL;
		}
		Collection(int x) {
			CurrentTree = 1;
			Trees[0] = new BinNode(x);
			for (int i = 1; i < maxTrees; i++)
				Trees[i] = NULL;
		}
		//第i个BinTree的根节点的值
		int GetVal(int i) {
			if (Trees[i] == NULL)return INTMAX;
			return Trees[i]->element;
		}
		//判断是否为空
		bool empty() {
			return CurrentTree == 0;
		}
		//查找当前Binomial Queue中的最小值
		int GetMin() {
			int ans = INT_MAX;
			for (int i = 0, bit = 1; bit <= CurrentTree; i++, bit <<= 1)
				if (GetVal(i) < ans)ans = GetVal(i);
			return ans;
		}
		//查找当前Binomial Queue中的最小值对应的下标
		int GetMinIndex() {
			int ans = INTMAX;
			int index = 0;
			for (int i = 0, bit = 1; bit <= CurrentTree; i++, bit <<= 1)
				if (GetVal(i) < ans)ans = GetVal(i), index = i;
			return index;
		}
	};
	typedef Collection* BinQueue;

	BinQueue now;

	//合并两棵大小相等的树T1,T2
	BinTree CombineTrees(BinTree T1, BinTree T2) {
		//将根节点大的树添加到根节点小的树的上面
		if (T1->element > T2->element)
			return CombineTrees(T2, T1);
		//此时,将T2添加到T1上面
		T2->NextSibling = T1->LeftChild;
		T1->LeftChild = T2;
		return T1;
	}

	//合并两个Binomial Queue
	BinQueue Merge(BinQueue H1, BinQueue H2) {
		BinTree T1, T2, Carry = NULL;
		if (H1->CurrentTree + H2->CurrentTree > maxSize) {
			printf("Out of Space");
			return NULL;
		}
		H1->CurrentTree += H2->CurrentTree;
		for (int i = 0, bit = 1; bit <= H1->CurrentTree; i++, bit <<= 1) {
			T1 = H1->Trees[i];
			T2 = H2->Trees[i];
			switch (4 * (!!Carry) + 2 * (!!T2) + (!!T1)) {
			case 0://000,都没有 ==> 不变
				break;
			case 1://001,只有T1 ==> 不变
				break;
			case 2://010,只有T2 ==> 将T2赋值给T1
				H1->Trees[i] = T2;
				H2->Trees[i] = NULL;
				break;
			case 3://011,有T1,T2 ==> 将T1,T2合并后,赋值给Carry
				Carry = CombineTrees(T1, T2);
				H1->Trees[i] = NULL;
				H2->Trees[i] = NULL;
				break;
			case 4://100,只有Carry ==> 将Carry赋值给T1
				H1->Trees[i] = Carry;
				Carry = NULL;
				break;
			case 5://101,有T1,Carry ==> 将T1,Carry合并后,赋值给Carry
				Carry = CombineTrees(T1, Carry);
				H1->Trees[i] = NULL;
				break;
			case 6://110,有T2,Carry ==> 将T2,Carry合并后,赋值给Carry
				Carry = CombineTrees(T2, Carry);
				H2->Trees[i] = NULL;
				break;
			case 7://111,,有T1,T2,Carry ==> 将Carry赋值给H1; 将T1,T2合并后,赋值给Carry
				H1->Trees[i] = Carry;
				Carry = CombineTrees(T1, T2);
				H2->Trees[i] = NULL;
				break;
			}
		}
		return H1;
	}

	//删除当前Binomial Queue中的最小值
	void DeleteMin(BinQueue H) {
		if (H->empty()) {
			printf("The Binomial Queue is empty\n");
			return;
		}
		//找到H的最小值,及其对应的下标
		BinNode* DeletedTree, * OldRoot;
		int index = H->GetMinIndex();
		int minItem = H->GetVal(index);

		//将该BinTree取出并删除
		//删除该树后的BinQueue即为H'
		DeletedTree = H->Trees[index];
		H->Trees[index] = NULL;

		//将该BinTree的根节点删除
		OldRoot = DeletedTree;
		DeletedTree = DeletedTree->LeftChild;
		delete OldRoot;

		//创建H''
		BinQueue DeletedQueue;
		DeletedQueue = new Collection();
		//由于H''是B_{index}树删除根节点之后的所有节点
		//因此其包含了B_0 ~ B_{index-1}
		DeletedQueue->CurrentTree = (1 << index) - 1;
		//将原来BinTree中的树拆开,赋值给H''
		for (int j = index - 1; j >= 0; j--) {
			DeletedQueue->Trees[j] = DeletedTree;
			DeletedTree = DeletedTree->NextSibling;
			DeletedQueue->Trees[j]->NextSibling = NULL;
		}

		//计算H'的CurrentTree
		H->CurrentTree -= DeletedQueue->CurrentTree + 1;
		//将H'与H''合并
		H = Merge(H, DeletedQueue);
	}
public:
	BinomialQueue() {
		now = new Collection();
	}
	void reset() {
		now = new Collection();
	}
	void Insert(int x) {
		BinQueue tmp = new Collection(x);
		now = Merge(now, tmp);
	}
	int top() {
		return now->GetMin();
	}
	void pop() {
		DeleteMin(now);
	}
};
BinomialQueue q;