ADS06:回溯&搜索策略
Back Tracking 回溯
一、基本思想
- 假设有一个部分解\((x_1,...x_i)\in S_k\)。
- 首先,我们添加\(x_{i+1} \in S_{i+1}\)
- 判断\((x_1,...,x_i,x_{i+1})\)是否符合条件
- 如果符合条件,则接着添加\(x_{i+2}\)
- 如果所有\(x_{i+2}\)均不符合条件,则将\(x_{i+1}\)剔除\(S_{i+1}\),然后,选择另一个\(x_{i+1}\)
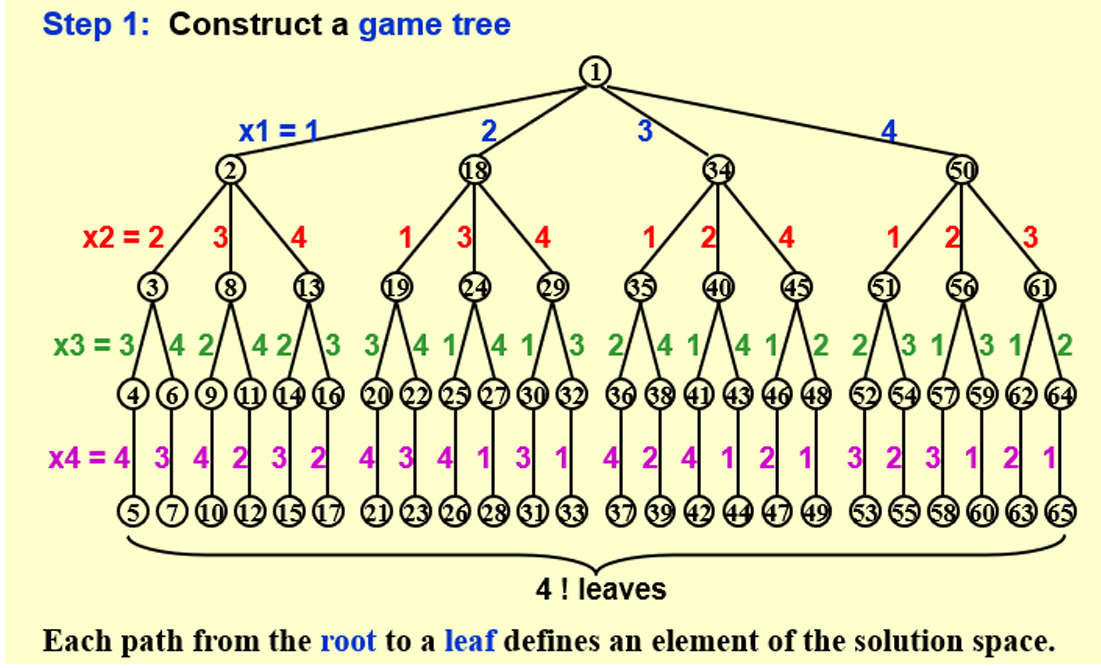
二、八皇后问题
2.1 约束
- \(S_i={1,2,3,4,5,6,7,8}\)
- 若\(i \neq j\),则\(x_i \neq x_j\)
- \(\frac{x_i-x_j}{i-j}\neq \pm1\)
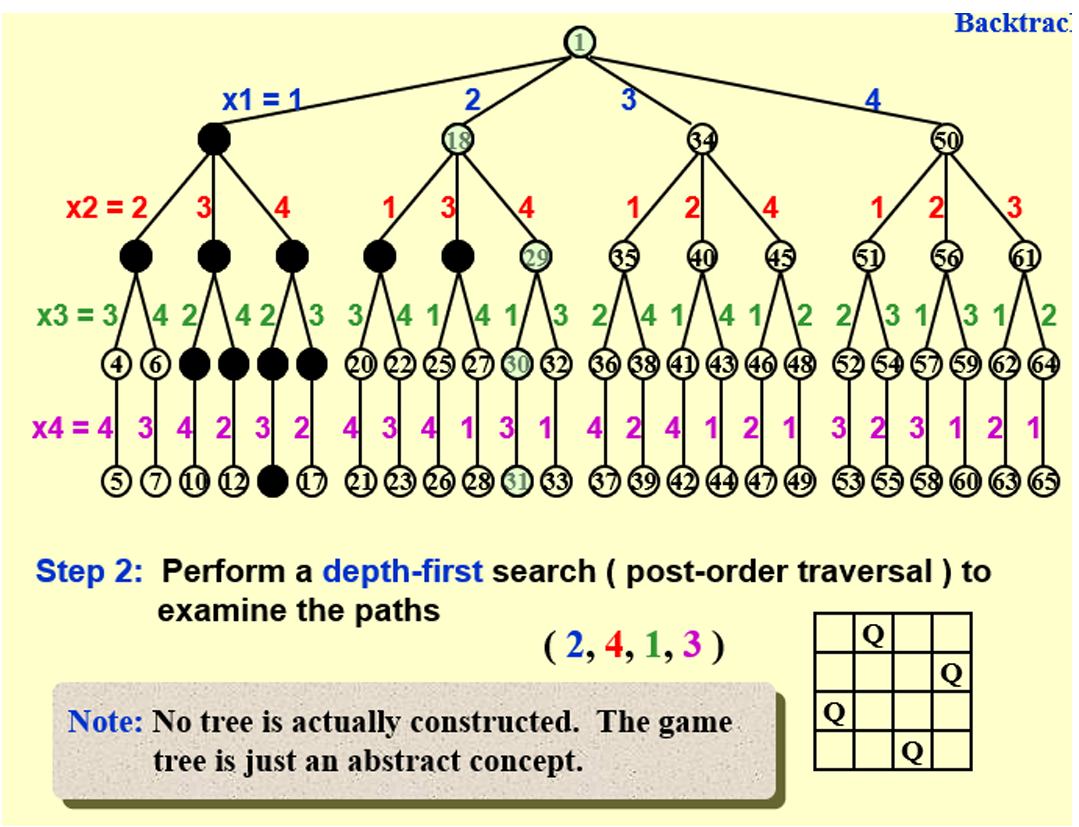
2.2 搜索树
三、收费公路重建问题
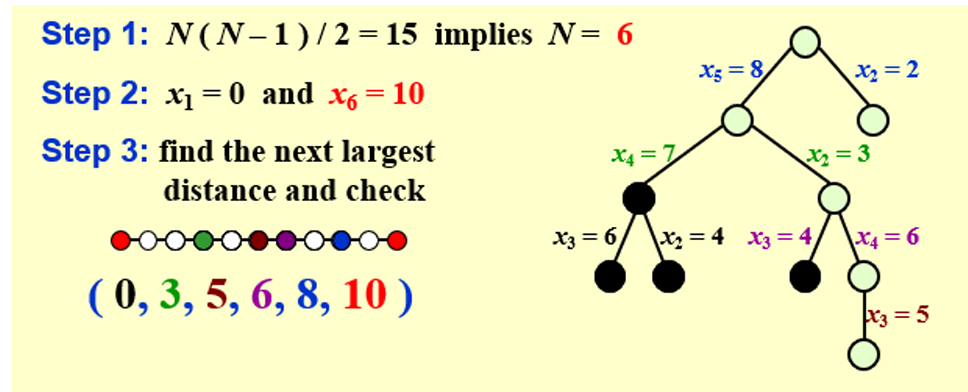
3.1 问题描述
给定\(x\)轴上的n个点,坐标为\(x_1<x_2<...<x_n\)
此时,每对点之间有\(\frac{n*(n-1)}{2}\)个距离
假设\(x_1=0\),给定\(\frac{n*(n-1)}{2}\)个距离,计算每个点的坐标
3.2 搜索算法
- 找出最大距离,就是整条路经的长度(\(x_0 ==> x_n\))
- 然后找出次大距离,这是下一个点到起点/终点的距离
- 接着在剩下的距离中找最大的距离,这是下一个点到起点/终点的距离
- ……
在这种算法中,可以保证每一步的枚举,最多有两种可能性
3.3 代码
bool Reconstruct ( DistType X[ ], DistSet D, int N, int left, int right ){ |
四、回溯的模板
bool Backtracking ( int i ){ Found = false; |
搜索策略
先找更小的\(S_i\)
一、评估函数
井字棋的评估函数:
\(f(P) =W_{computer}-W_{Human}\)
其中,\(W\)表示在情况\(P\)时,可能会赢的结果(横着三个/竖着三个/斜着三个)
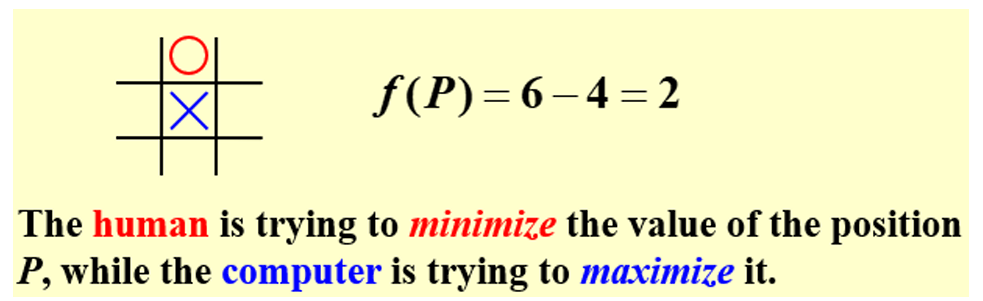
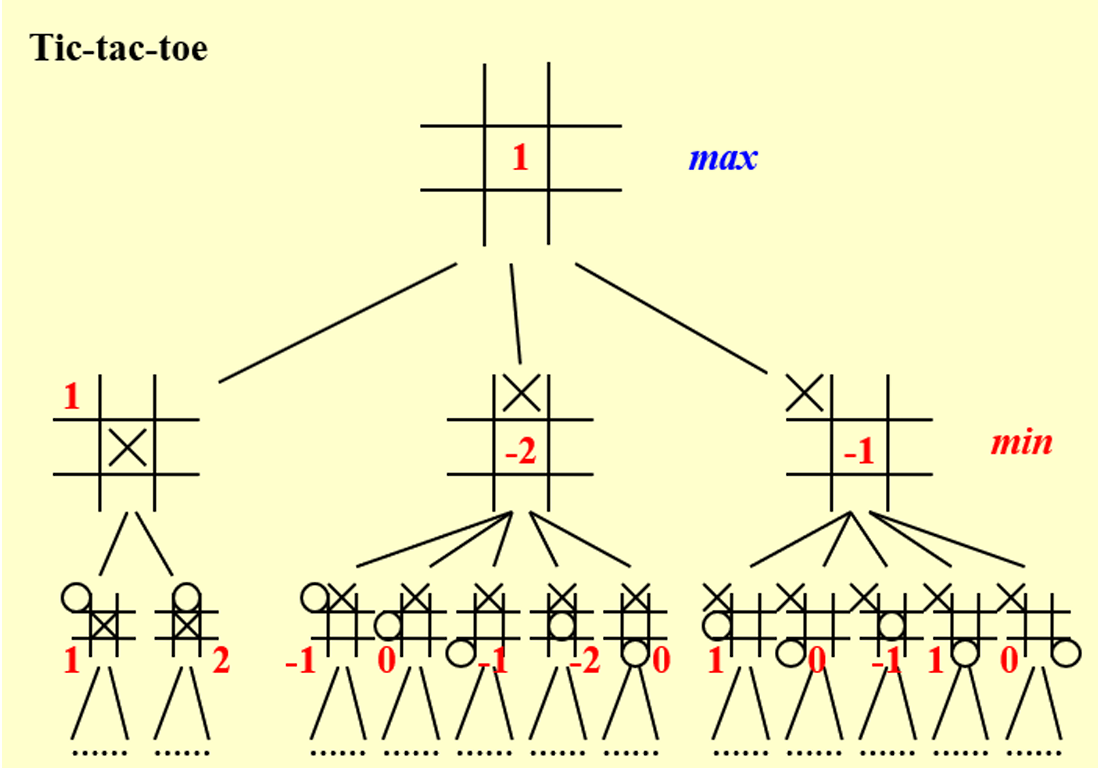
二、\(\alpha\)-\(\beta\)剪枝
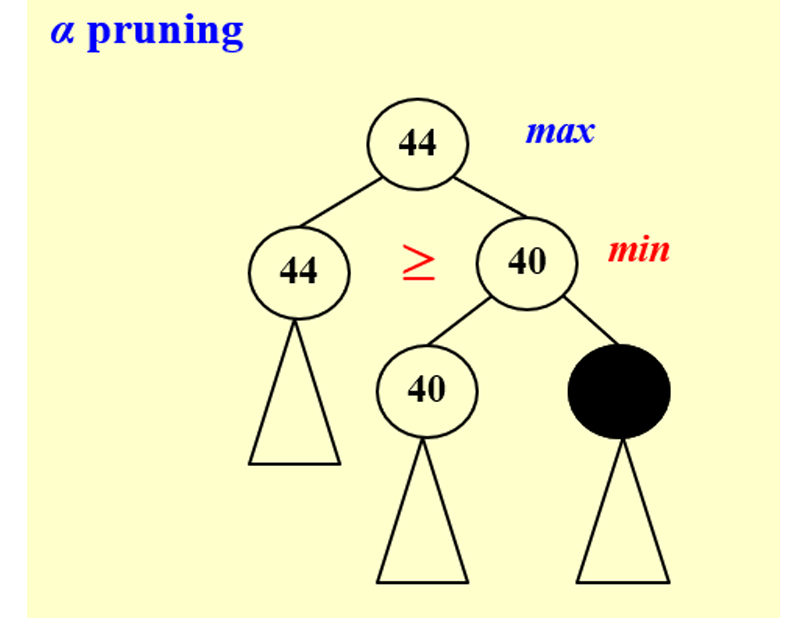
2.1 \(\alpha\) pruning
根节点取子节点的最大值,子节点取其子节点的最小值
当一个子节点的子节点已经算出来小于同层次的其它值时,此时该节点一定会被放弃,因此不需要计算其它子节点了
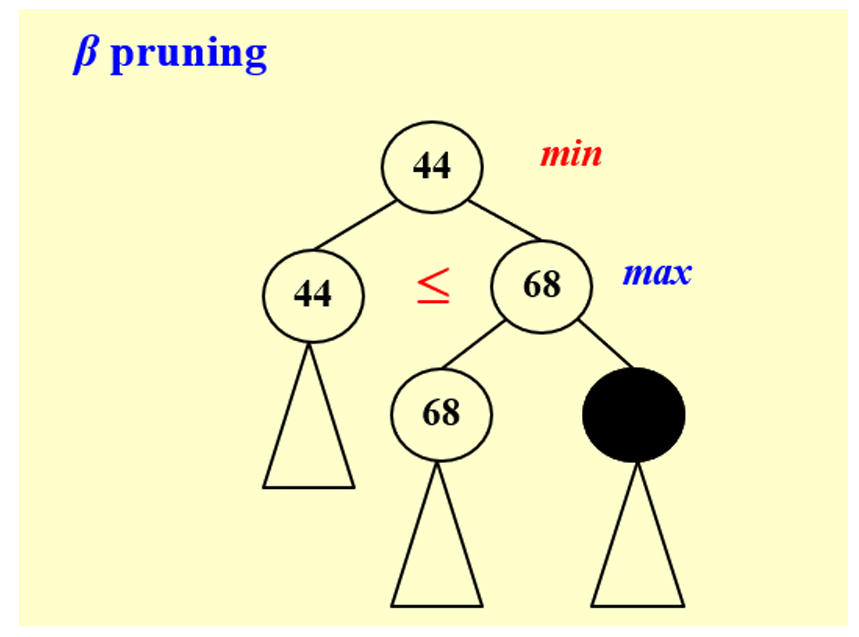
2.2 \(\beta\) pruning
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 华风夏韵!
评论