分治法

一、主体思想

将问题\(T(N)\)分解为\(a\)个子问题
通过递归的方法解决子问题，时间复杂度为\(T(\frac{N}{b})\)
将子问题的解合并，得到原始问题的解，时间复杂度为\(f(N)\)

一般的递归：\(T(N) =aT(\frac{N}{b})+f(N)\)

降低算法时间的关键：\(f(N)\)

二、分析算法的时间复杂度

2.1 asymptotic analysis 渐进分析

省略常数项
省略低阶项

2.2 Random Access Model–RAM：随机访问模式

单元操作，如**+、-、*、/、=、内存读取**，所需时间为常数

三、Closest Points Problems

3.1 问题描述

给定n个点，求这n个点两两之间的最短欧氏距离

3.2 解决思路

将n个点分成两组，每组n/2个点，满足\(x_1\leq x_2\leq...\leq x_n\)，记为\(L_x,R_x\)
递归解决两组的最短距离
将子问题合并为原问题

3.3 合并操作

设\(\delta = min(CPP(L_x),CPP(R_x))\)，将\(L_x,R_x\)中，与中心距离\(<\delta\)的点分别取出，记为\(T_l,T_r\)，令\(T=T_l \bigcup T_r\)

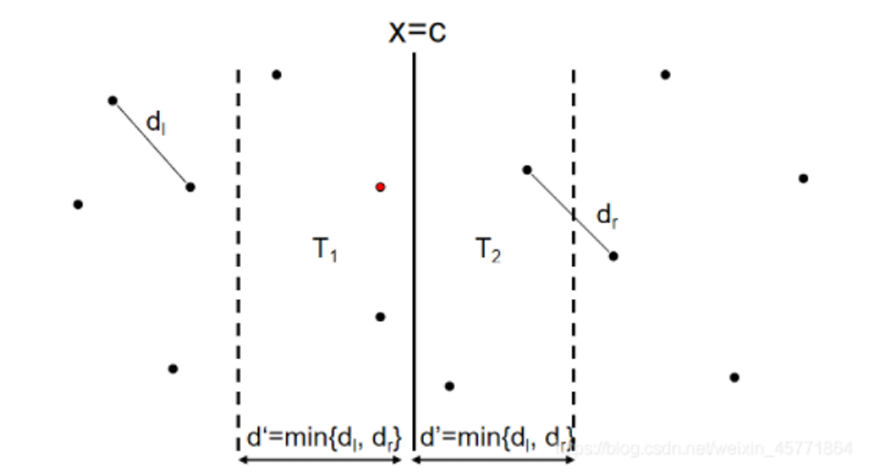
假设\(\exist P_l\in S_l,P_r \in S_r\)，使得\(dist(P_l,P_r)=D<\delta\)，则可以得出以下性质

性质1：\(P_l\in T_l,P_r\in T_r\)，即这两点一定在中线两侧

如果\((P_l,P_r)\)属于同一侧，表明在\(T_l\)或\(T_r\)的一侧能够找到两个点，使其距离<\(\delta\)，与\(\delta\)的定义矛盾

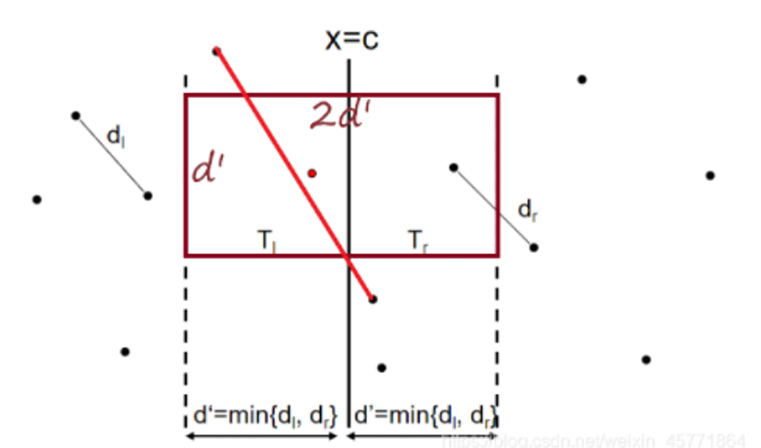
性质2：任意一对\(P_l,P_r\)，一定存在一个以中线为轴的\(2\delta*\delta\)的矩形区域，将它们包含在内

假设\(P_l,P_r\)没有位于该区域，以图中所示的红线相连的两个点为例

可见，其距离一定会大于\(\delta\)，即\(dist(P_l,P_r)>\delta\)，与\(dist(P_l,P_r)=D<\delta\)矛盾

性质3：以中线为轴的\(2\delta*\delta\)的矩形区域内至多包含T中的6个点，且\(T_l\)和\(T_r\)中各至多有4个

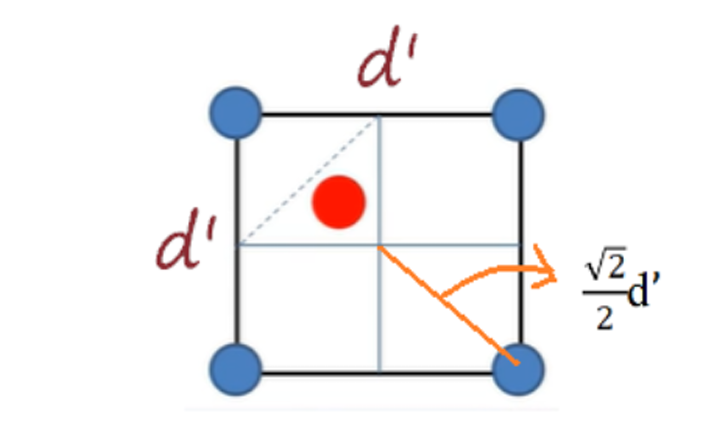
取\(2\delta*\delta\)矩形的右半边出来，即为\(\delta*\delta\)的小矩形

假设已经有4个点分布在这个矩形的四个角，那么矩形内部无法再有任何点的存在。因为这个小矩形\(\in T\)，假设如果小矩形内还有一个红点，令其与其余四点的距离均最远，那么红点必定位于小矩形的中心位置，距离其余四点的距离为\(\frac{\sqrt{n}}{2}\delta\)，与\(\delta\)的定义矛盾。

因此，左右两边的小矩形最多有4个点。而由于两个小矩形会有两个点重合，因此\(2\delta*\delta\)的矩形区域内至多有6个点

根据上述性质，我们可以得出：

(1)如果把\(T\)中的点按照\(Y\)坐标升序排序，任取一点\(T[i]\)，\(T[i+7]\)与\(T[i]\)的距离一定超过\(\delta\)

(2)如果把\(T_l\)中的点按照\(Y\)坐标升序排序，任取一点\(T_l[i]\)，\(T_l[i+5]\)与\(T_l[i]\)的距离一定超过\(\delta\)，\(T_r\)同理

合并的具体操作

设\(\delta = min(CPP(L_x),CPP(R_x))\)，将\(L_x,R_x\)中，与中心距离\(<\delta\)的点分别取出，记为\(T_l,T_r\)，令\(T=T_l \bigcup T_r\)
将\(T\)中的点按照\(Y\)坐标升序排列，对每一个\(T[i]\)，计算其与\(T[i+1] →T[i+6]\)的距离，并更新答案

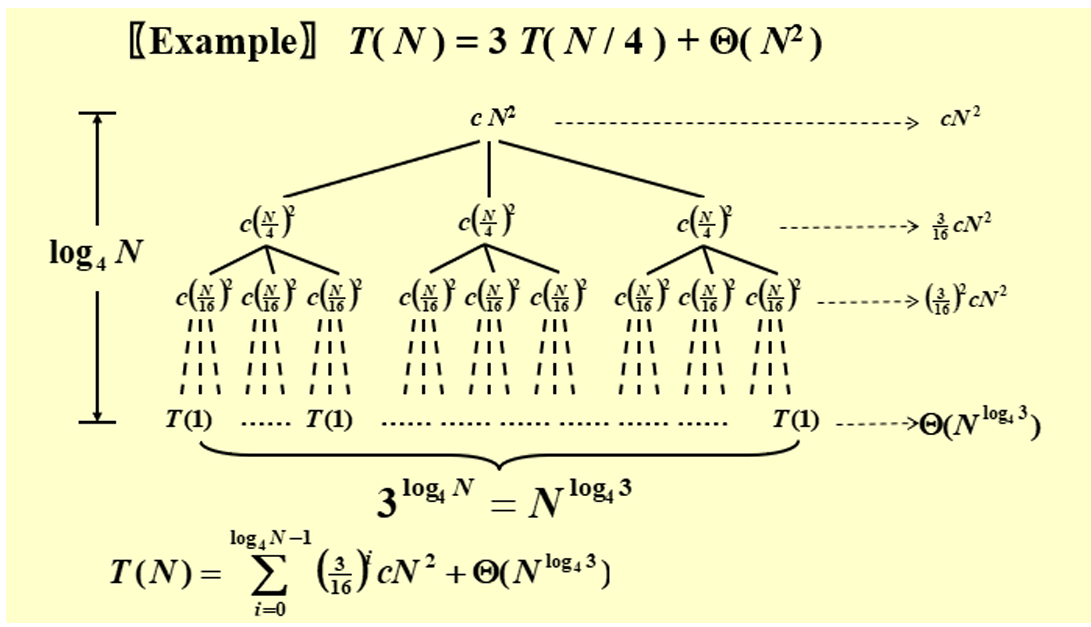
四、递归树 Recursion-tree method

树的每一个节点，表示该节点消耗的时间
整个问题消耗的时间，为所有节点加起来的结果

例：\(T(n)=2T(\frac{n}{2})+\frac{n}{log\ n}\rightarrow O(nlog\ log\ n)\)

\[ \begin{aligned} T(n)&=2T(\frac{n}{2})+\frac{n}{log\ n} \\ &=\frac{n}{log\ n}+2*\frac{n/2}{log\ n/2}+...+2^k*\frac{n/2^k}{log\ n/2^k} \\ &=\sum_{k=0}^{log\ n}2^k*\frac{n/2^k}{log\ n/2^k} \\ &=n*\sum_{k=0}^{log\ n} \frac{1}{log\ n/2^k} \\ &=n*\sum_{k=0}^{log\ n} \frac{1}{log\ n - k*log\ 2} \\ &=n*\sum_{k=0}^{log\ n}\frac{1}{log\ n - k} \\ &=n*\sum_{k=0}^{log\ n}\frac{1}{k} \\ &=n*(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{log\ n})\\ &=n*log log\ n \end{aligned} \]

例：\(T(n)=8*T(\frac{n}{2})+O(1),n^2\geq m; m,n^2< m \rightarrow O(\frac{n^3}{\sqrt m})\)

建立递归树：

树的每一个节点的时间复杂度为\(O(1)\)
树的每一层有\(8^k\)个节点
\(n^2>m \rightarrow \frac{n}{\sqrt m}>1\)，因此树有\(log\frac{n}{\sqrt m}\)层

时间复杂度为：\(8^{log\frac{n}{\sqrt m}}*m=O(\frac{n^3}{\sqrt m})\)

例：\(T(n)=T(\frac{n}{6})+T(\frac{7n}{9})+O(n) \rightarrow O(n)\)

\(T(n)=2T(\frac{n}{6}) + O(n)\)：\(a=2,b=6,N^{log_ba}=N^{log_62}<N\) => \(T(N)=O(N)\)

\(T(n) = 2T(\frac{7n}{9}) + O(n)\)：\(a=2,b=\frac{9}{7},N^{log_ba}=N^{log_{\frac{9}{7}}2}>N\) => \(T(N)=O(N^{log_{\frac{9}{7}}2})=O(N^{2.75})\)

五、主定理

5.1 f(N)直接给出

设\(T(N)=aT(\frac{N}{b})+f(N)\)，则

若\(f(N)<O(N^{log_ba})\)，则\(T(N)=\Theta(N^{log_ba})\)
若\(f(N)=O(N^{log_ba})\)，则\(T(N)=\Theta(f(N)*log_bN)\)
若\(f(N)>O(N^{log_ba})\)，则\(T(N)=\Theta(f(N))\)

5.2 f(N)为递归表示

设\(T(N)=aT(\frac{N}{b})+f(N)\)，则

若\(f(N)<af(\frac{N}{b})\)，则\(T(N)=\Theta(N^{log_ba})\)
若\(f(N)=af(\frac{N}{b})\)，则\(T(N)=\Theta(f(N)*log_bN)\)
若\(f(N)>af(\frac{N}{b})\)，则\(T(N)=\Theta(f(N))\)

5.3 f(N)直接给出

设\(T(N)=aT(\frac{N}{b})+\Theta(N^k log^p N)\)，且\(a\geq 1,b>1,p\geq 0\)，则

若\(a>b^k\)，则\(T(N)=O(N^{log_b a})\)
若\(a=b^k\)，则\(T(N)=O(N^k log^pN*log_bN)\)
若\(a<b^k\)，则\(T(N)=O(N^k log^{p}N)\)

例题

\[ \begin{aligned} &设m=log\ n,则2^m=n \rightarrow T(2^m)=2T(2^{\frac{m}{2}})+m \\ &设G(m)=T(2^m),则 \\ &原式转化为:G(m)=2G(\frac{m}{2})+m=O(mlog\ m)\\ &又\because m=log\ n\\ &\therefore T(n)=O(log\ n*log\ log\ n) \end{aligned} \]