动态规划 Dynamic Programming

一、设计DP的方法

(1)描述最优的解决方案

(2)递归定义最优解

(3)按照某一顺序进行计算

(4)重新构造解决策略

二、动态规划的要求

(1)子问题之间有重复

(2)子结构之间保持最优性：问题由子问题的最优解构成

三、动态规划的方法

(1)上到下：Memorization，记忆化，将计算过的结果储存下来

(2)下到上：Tabulation，表格法，迭代的方法构造问题的解

四、Ordering Matrix Multiplications

1 矩阵乘法的定义

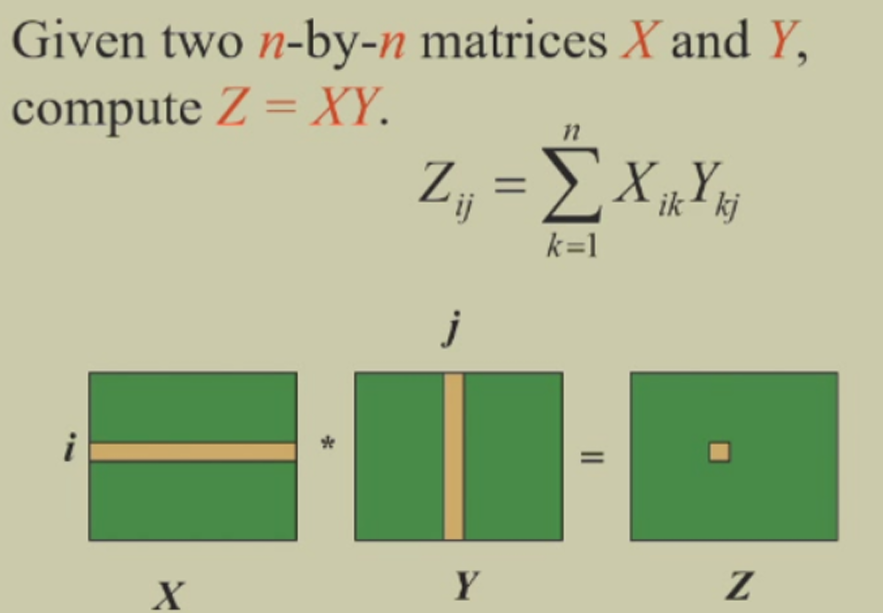
image-20240521180937829

2 矩阵链式相乘的顺序与计算次数的关系

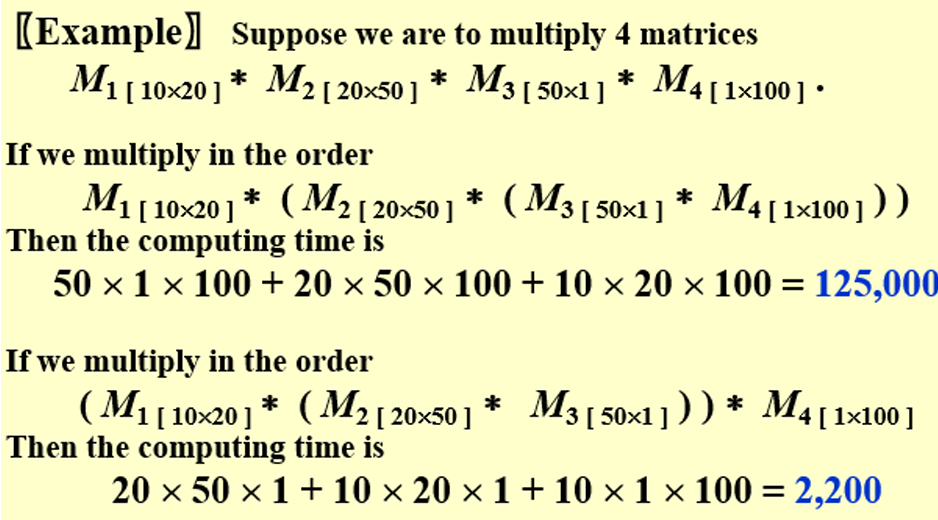
image-20240521180950325

3 问题描述

我们用什么样的顺序，可以用最少的计算时间，来计算n个矩阵的乘积

4 n个矩阵相乘的可能顺序

(1)设\(b_n\)表示：n个矩阵\(M_1*M_2*...*M_n\)的可能顺序，则\(b_2=1,b_3=2,b_4=5\)，可以计算出\(b_n=O(\frac{4^n}{n\sqrt n})\)（卡特兰数）

(2)设\(M_{ij}=M_i*...*M_j\)，则\(M_{1n}=M_1*...*M_n\)

(3)假设我们需要乘n个矩阵\(M_1*...*M_n\)，其中\(M_i\)是一个\(r_{i-1}*r_i\)的矩阵

(4)设\(m_{ij}\)表示：\(M_i*...*M_j\)的最优解，则可以得到递归关系 \[ m_{ij}= \begin{cases} 0,&\text{if\ i = j}\\ min_{i\leq k < j}\{m_{ik}+m_{kj}+r_{i-1}r_kr_j\},&\text{if\ j>i} \end{cases} \]

五、Floyd-Warshall多源最短路算法(没有负环)

(1)设\(D^k[i][j]\)表示：从 \(i\) 到 \(j\) 的最短路，且只经过编号\(\leq k\)的点

​ 且\(D^{-1}[i][j]\)表示：从 \(i\) 到 \(j\) 的边的边权

​ \(D^{n-1}[i][j]\)表示：从 \(i\) 到 \(j\) 的边的最短路

(2)子问题的转移：

​ (a)对于第k个点， 有两种情况

​ A. \(k\notin\)最短路，则\(D^k[i][j]=D^{k-1}[i][j]\)

​ A. \(k\in\)最短路，则\(D^k[i][j]=D^{k-1}[i][k]+D^{k-1}[k][j]\)

​ (b)因此，\(D^k[i][j]=min\{ D^{k-1}[i][j],D^{k-1}[i][k]+D^{k-1}[k][j]\}\)

void Floyd(){
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
            D[i][j]=a[i][j];
    for(int k=0;k<n;k++)
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
                D[i][j]=min(D[i][j],D[i][k]+D[k][j]);
}

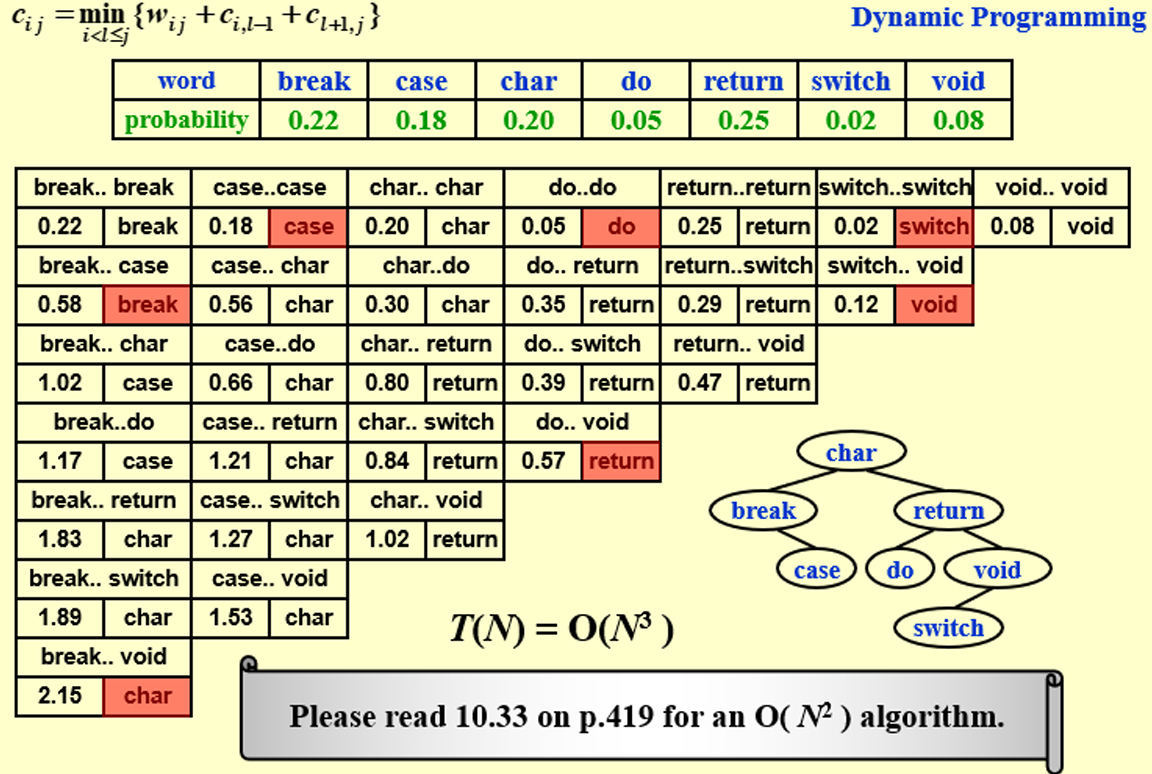
六、最优二叉查找树

6.1 问题描述

给定\(n\)个数\(w_1<w_2<...<w_n\)，\(w_i\)的查找频率为\(p_i\)

构造一个二叉查找树，满足查找的消耗最小

查找的消耗定义为：\(T(n)=\sum_{i=1}^n p_i*(1+deep_i)\)

image-20240521181007300

6.2 求解思路

(1)定义\(T_{ij}\)表示：\(w_i...w_j\)的最优二叉查找树

​ 定义\(c_{ij}\)表示：\(T_{ij}\)的消耗，\(c_{ii}=0\)

​ 定义\(r_{ij}\)表示：\(T_{ij}\)的根节点

​ 定义\(w_{i}\)表示：\(T_{ij}\)的权值和，\(w_{ij}=\sum_{k=i}^j p_k\)

(2)转移方程： \[ \begin{aligned} c_{ij}&=(1*p_k)+(cost(L)+cost(R))+(weight(L)+weight(R)) \\ &(查找根节点的开销)+(查找左右子树原来的开销)+(由于左右子树变深了一层,故其开销要变大) \\ &=p_k+c_{i,k-1}+c_{k+1,j}+w_{i,k-1}+w_{k+1,j}\\ &=w_{ij}+c_{i,k-1}+c_{k+1,j}\\ &=min_{i<k\leq j}\{ w_{ij}+c_{i,k-1}+c_{k+1,j} \} \\ r_{ij}&=k,当且仅当c_{ij}=w_{ij}+c_{i,k-1}+c_{k+1,j}在k时取得最小值 \end{aligned} \] image-20240521181020187

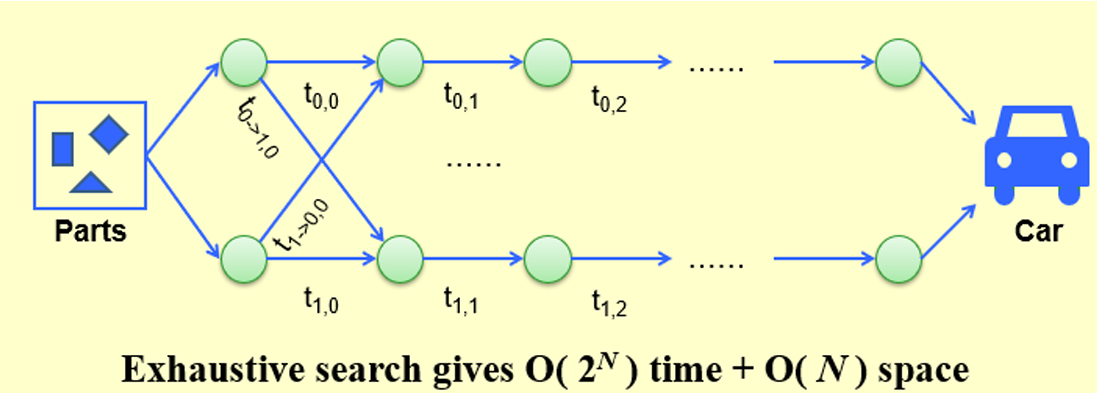
七、产品组装

7.1 问题描述

同一辆车有两条生产线，每个阶段所需的时间不同

人们可以在阶段之间改变生产线，但是改变生产线需要一定的时间

求：最短的组装时间

image-20240521181033367

7.2 解决思路

(1)定义\(f[i][j]\)表示：从起点到状态\(t_{i,j}\)所需的最短时间

(2)转移方程： \[ \begin{aligned} f[0][j]&=min\{f[0][j-1]+t[0][j],f[1][j-1]+t[1->0][j-1] \} \\ f[1][j]&=min\{f[1][j-1]+t[1][j],f[0][j-1]+t[0->1][j-1] \} \end{aligned} \]

八、不能使用DP的问题

(1)子问题之间有相互依赖关系：如从不同状态转移到当前状态，会导致当前状态的消耗不同

(2)子问题之间的依赖关系，会形成一个环

例题：背包问题

有n个物品，每个物品的大小为size[i]，价值为value[i]，求当size和不超过C时的最大价值

  1. 定义OPT(i,v)表示：在1~i中进行选择，总价值为v的时候占据的最小空间
$OPT(i,v)=\min\{OPT(i-1,v), OPT(i-1,v-value[i])+size[i]\}$
  1. 定义OPT(i,C)表示：在1~i中进行选择，占据空间不超过C时的最大价值
$OPT(i,C)=\max\{OPT(i-1,C), OPT(i-1,C-size[i])+value[i]\}$