ADS09：贪心算法

贪心算法 Greedy Algorithm

一、优化问题 Optimization Problems

1. 给出一组约束条件和一个优化函数
2. 可行解：满足约束条件的解称为可行解
3. 最优解：优化函数具有最佳可能值的可行解称为最优解

二、贪心算法 Greedy Method

1. 在一定的贪心准则下，每个阶段做出最佳决策

2. 在一个阶段做出的决定，在以后的阶段不会改变，所以每一个决定都应该确保可行性

三、活动的选择问题 Activity Selection Problem

3.1 问题描述

给定一系列活动\(S=\{a_1,a_2,...a_n\}\)，每个活动\(a_i\)有一个持续区间\([s_i,f_i)\)

要求在活动的持续区间不重叠的情况下，选择数目最多的活动

3.2 DP算法

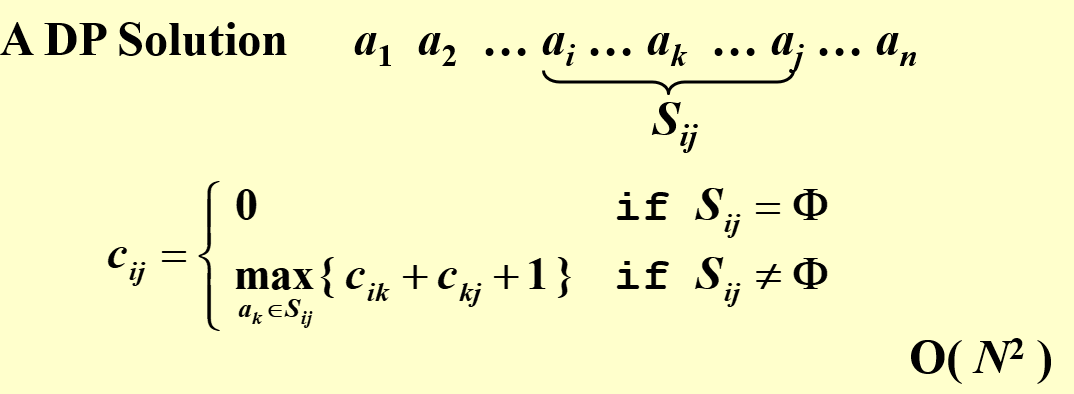
3.3 贪心算法

3.3.1 算法1：找最先来的

3.3.2 算法2：找最短的

3.3.3 算法3：找冲突最少的

3.3.4 算法4：找结束最早的

3.3.5 对算法4的证明

证明思路：有一组最优解与算法4的结果相同

证明：假设贪心算法选出了n个活动\(G_n\)，最优解选出了m个活动\(O_m\)，且\(m\ge n\)

• 当选第1个活动的时候，由于算法要求，\(G_1\)的结束时间一定\(\leq\)\(O_1\)的结束时间

• 假设选第k个活动时，\(G_{1→k}\)的结束时间均满足\(\leq\)\(O_{1→k}\)的结束时间，则选第\(k+1\)个活动的时候，根据贪心策略，\(G_{k+1}\)的结束时间一定\(\leq\)\(O_{k+1}\)的结束时间

• 根据上述要求，如果\(O_m\)包含的点数比\(G_n\)多，那么剩余的活动，\(G_n\)也一定能够选择，产生了矛盾，因此\(G_n\)包含的数目与\(O_n\)相同

3.4 如果每个活动有一个权重，要求权重和最大

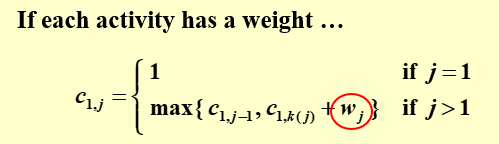
四、哈夫曼编码 Huffman Code

4.1 贪心思想

将出现频率高的字母，赋予较短的编码

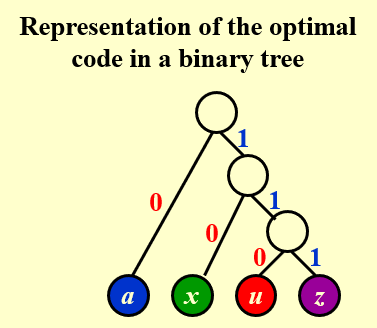
4.2 二叉树表示

普通编码：

贪心算法：

4.3 从编码翻译出原文

要求：所有字母的编码，都不是另一个字母的编码的前缀prefix

前缀prefix：一个字母的编码，完全包含另一个字母的编码

方法：将按照二叉树表示，让每一个字母作为二叉树的叶子节点，编码根据路径确定

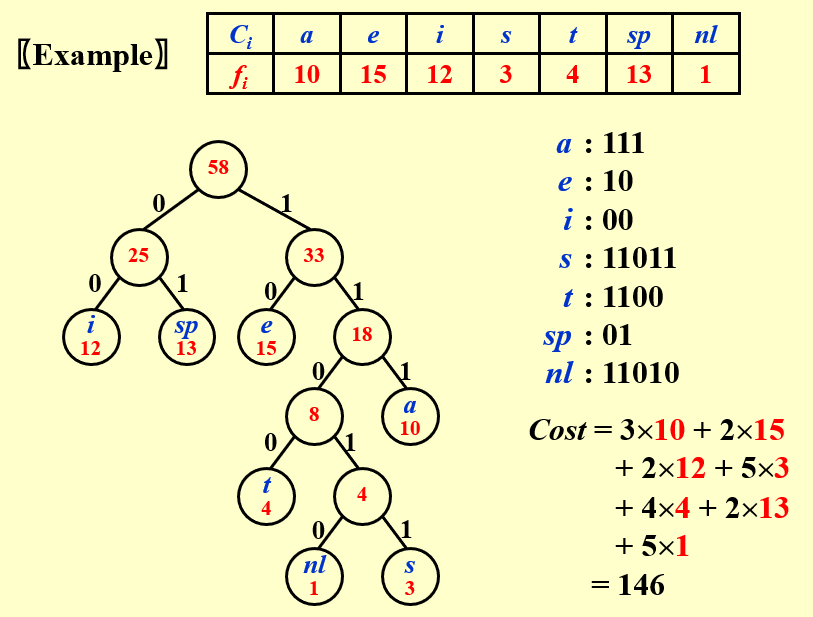
4.4 哈夫曼编码的算法

1. 在n个节点的集合\(S\)中，选择出现频率最低的两个点
2. 频率较低的作为右儿子，较高的作为左儿子
3. 为这两个点建立一个父节点，其频率为两个儿子的和，然后插入到原来的节点集合\(S\)中
4. 重复上述步骤，直到只剩下一个点
5. 这样便建立出了Huffman Tree

4.5 最优解的证明

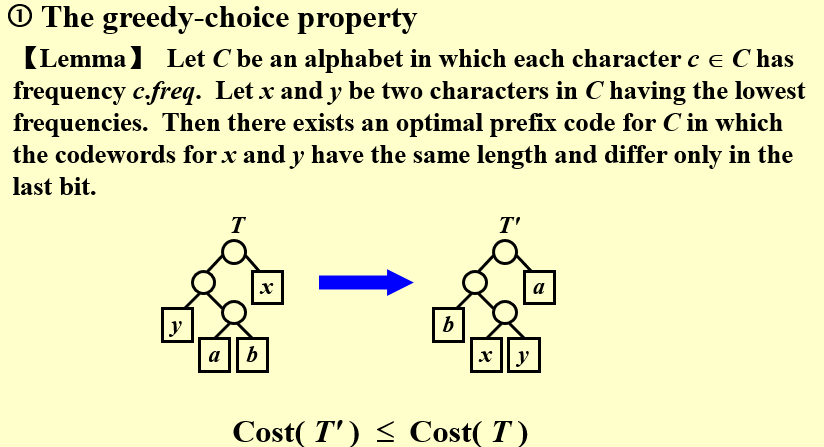
引理1：频率低的节点一定放在最下面

1. 设\(C\)是一个字符集，每一个字符\(c\in C\) 有一个频率\(c.freq\)
2. 设\(x\)和\(y\)为\(C\)中频率最小的两个点
3. 则存在一个最优的前缀编码，其中\(x\)和\(y\)的编码与贪心的编码长度相同，并且只有最后一位可能不同

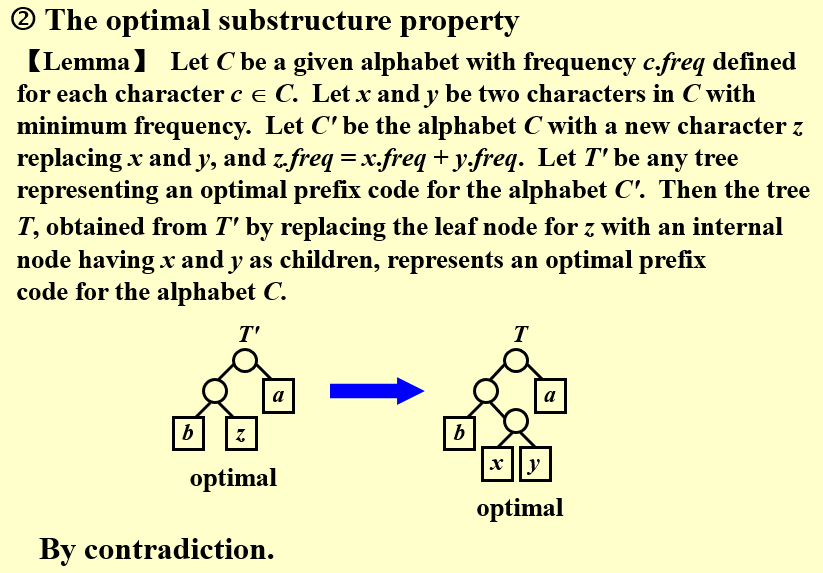
引理2：将两个点压缩为一个点后，原来的最优解与现在的最优解相同

1. 设\(C\)是一个字符集，每一个字符\(c\in C\) 有一个频率\(c.freq\)
2. 设\(x\)和\(y\)为\(C\)中频率最小的两个点
3. 将字符集\(C\)中的\(x\)和\(y\)用\(z\)替换(\(z.freq=x.freq+y.freq\))，产生一个新的字符集\(C'\)
4. 设\(T'\)表示字符集\(C'\)的一个最优前缀编码
5. 将\(T'\)中表示\(z\)的叶节点，替换成一个以\(x\)和\(y\)为子节点的叶节点，产生一个新的前缀编码\(T\)，则\(T\)表示\(C\)的一个最优前缀编码