NP完全性 NP-Completeness

一、基础概念

1.1 可计算的问题

  1. computational problem：可以通过计算机，一步一步的在有限时间内解出答案。分为以下4类
    1. Decision problem：判断是否存在一个可行解
    2. Search problem：找到一个可行解
    3. Optimization problem：找到一个最优的可行解
    4. Counting problem：计算有多少种可行解
  2. 事实：
    1. Decision problem比Optimization problem简单
      1. 如果优化问题有解，则判定问题必然有解
      2. 如果判定问题很难，则优化问题必然很难
    2. 对于每一个优化问题\(X\)，通过加一些边界，可以将其转化为一个判定问题\(X'\)
  3. 当我们定义\(P\)和\(NP\)问题的时候，我们只考虑判定问题

1.2 简单or难问题

  1. easy problem：多项式时间内，可以解决
  2. hard problem：指数时间甚至更长

1.3 问题的编码

  1. 通过二进制字符串，将问题的输入重新编码encode
  2. Input Size：将输入编码为二进制串后，输入的大小即为二进制串的长度
  3. polynomial-time algorithm：最坏的运行时间为\(O(n^k)\)
  4. Polynomial-Time Solvable Problems：存在一个多项式时间的算法，可以正确的解决所有的输入

二、Machine：计算的模型

2.1 Turing machine

  1. Turing machine：有若干条纸带和若干个针头，下一步取决于之前的状态，有限个状态的控制

2.2 Random Access Machine(RAM)

  1. Random Access Machine(RAM)：

    1. 有一个控制器，多个寄存器，一个内存
    2. 每个寄存器和内存存储一个整数
    3. 对寄存器进行算术/比较运算，通过一个特殊的寄存器，从内存中读取/存入值，这些都视为一步
    4. 循环和子程序不考虑简单操作，他们是一系列单步运算

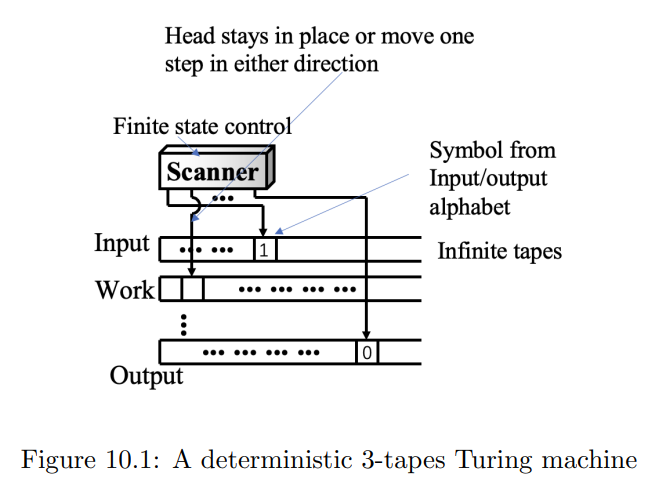
    image-20240611152934642

  2. 广义邱奇-图灵论题：

    1. 任何可以在物理上由一个计算机M在T(n)的时间内解决的language，都可以通过图灵机在\(O(T(n)^k)\)的时间内解决
    2. 其中，k只与M有关

2.3 Language：等价决策问题

  1. A language L over \(\sum\)：由Σ中的字符定义的任意一个字符串
  2. A language：语言是问题的形式化表达
  3. 图灵机M判定语言L：
    1. 当任意一个输入\(x \in L\)时，M停止在accepting的状态
    2. 当任意一个输入\(x \notin L\) 时，M停止在rejecting的状态
  4. 算法A接受x：A(x) = 1；算法A拒绝x：A(x) = 0
  5. 算法A判定语言L：
    1. 所有在L中的二进制串都被A接受
    2. 所有不在L中的二进制串都被A拒绝
  6. Decision problem or language X
    1. 问题X是一个字符串的集合
    2. 实例s是一个字符串
    3. 算法A决定问题X：\(A(s)=yes \harr s\in X\)

2.4 Nondeterministic Turing Machine：非确定性图灵机

​ 从历史上看，NDTM和标准TM之间的唯一区别是NDTM有两个转换函数δ0和δ1， NDTM可以在它们之间进行选择。

​ 我们赋予它一种神奇的能力，可以分裂成两个副本，每个副本都有不同的部分告诉它接下来要做什么。这些副本可以进一步分裂成指数级的副本或分支。

​ 如果任何一个分支接受了，那么我们就说机器作为一个整体接受了；如果没有，机器就会报废。

​ 一个非确定性图灵机可以自由地从一个有限集合中选择它的下一步。如果这些步骤中有一个找到了解决方案，它总是会选择正确的那一个。

  1. witness：提供了一系列选择，引导机器走向accepting的分支
  2. 语言L 被 非确定性图灵机 判定：
    1. 对于任意\(x \in L\)，存在一个witness w使得M(x,w)接受
    2. 对任意\(x \notin L\)，不存在一个witness w使得M(x,w)接受
  3. A verification algorithm A(x, y)：验证算法A(x,y)
    1. x：正常的输入
    2. y：证书
    3. 算法判断对于x，是否存在一个y，使得A(x,y)=1

三、 Complexity class

  1. P：可以在多项式时间内，解决的判定、解决问题
    1. 存在一个多项式时间的确定性算法A，能够判定L
  2. NP：可以在多项式时间内，判定是否为Yes；不能在多项式时间内，计算出来结果
    1. 存在一个非确定性多项式时间算法A，能够判定L
      1. 对于任意\(x \in L\)，A有一些不确定的走法选择，使A接受x
      2. 对任意\(x \notin L\)，没有走法选择，使A接受x
    2. 语言L有一个有效的证明者A(x, y)，算法A在多项式时间内验证语言L
      1. 对于任意\(x \in L\)，存在一个长度为|x|的多项式复杂度内的certificate y，使得A(x,y) = 1
      2. 对任意\(x \notin L\)，不存在y，使得A(x,y) = 1
  3. co-NP：可以在多项式时间内，判定是否为No，是NP问题的反面
  4. 定理：判断问题\(X \in P \harr \overline X \notin P\)
  5. 问题是否容易处理
    1. tractable易处理的：多项式时间内可以解决
    2. intractable不易处理的：需要指数的时间来解决

四、Reductions and NP-complete problems：归约和NP完全问题

  1. (Turing归约)问题A 可以归约到 问题B：\(A \le_T B\)
    1. 解决B的算法 可以用来 解决A
    2. A 比 B 容易
    3. 问题A可以转化为问题B的一个子问题
  2. (Cook归约)问题A 可以多项式归约到 问题B：\(A \le_P B\)
    1. 问题A 可以 归约到 B
    2. 可以通过多项式次调用B的子进程，然后进行多项式次运算 得到问题A的答案
    3. A 比 B 容易
  3. (Karp归约)：
    1. 如果存在一个多项式时间可以计算的函数f，使得对任意\(x∈L1 \harr f(x)∈L2\)，则L1可以多项式归约到L2
  4. 证明A可以多项式归约到B：
    1. 找到一个可以在多项式时间内计算的函数\(f\)
    2. 证明：若\(x∈A\)，则\(f(x)∈B\)
    3. 证明：若\(f(x)∈B\)，则\(x∈A\)；或者证明：若\(x\notin A\)，则\(f(x)\notin B\)
  5. NP-Hard问题
    1. \(\forall L'\in NP,L'\le_P L\)
  6. NP-Complete问题：
    1. \(\forall L'\in NP,L'\le_P L\)
    2. \(L \in NP\)
  7. 证明一个问题是NP-Complete问题
    1. 证明：\(L∈NP\)
    2. 选择一个NPC问题L‘，证明L’可以 多项式归约到 L

五、NPC问题

5.1 SAT问题

  1. 给定一个CNF的关系式Φ，判断是否存在一组变量的取值，使得Φ为真
  2. k-SAT：Φ有k个变量

5.2 clique问题

  1. 给定一个k，判断在图中是否有size为k的团

  2. 团：从图中选择一些点，这些点两两之间均有边相连

  3. 证明团问题是NPC问题：

    1. 证明：clique \(\in\) NP

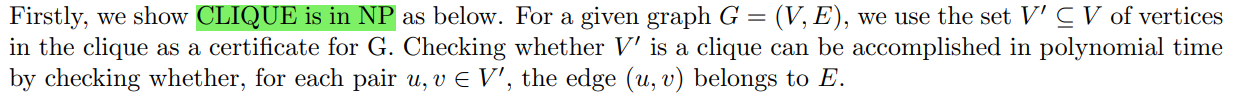
      image-20240611152948403

    2. 证明：3-SAT \(\le_P\) clique，即证明，3-SAT问题 可以转化成 clique的一个子问题

      image-20240611152953066

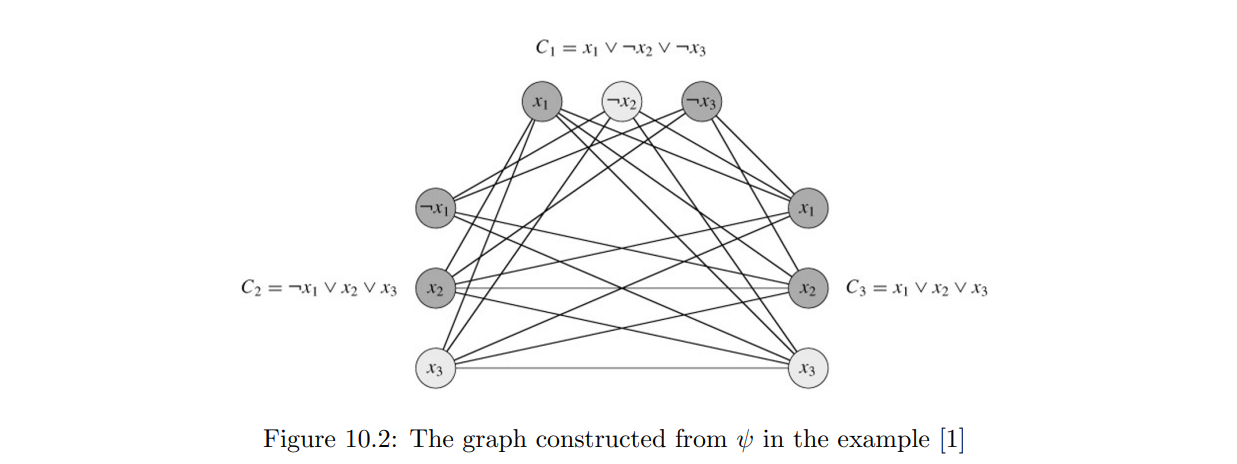
      image-20240611152957959

      image-20240611153003599

5.3 顶点覆盖问题

  1. 给定一个无向图G和一个整数K，判断G是否存在一个不超过K个节点的节点集合V‘，使得G中所有的边至少有一个顶点在V’中

  2. 证明vertex cover是NPC问题

    1. 证明：vertex cover \(\in\) NP

      image-20240611153009325

    2. 证明：clique \(\le_p\) vertex cover

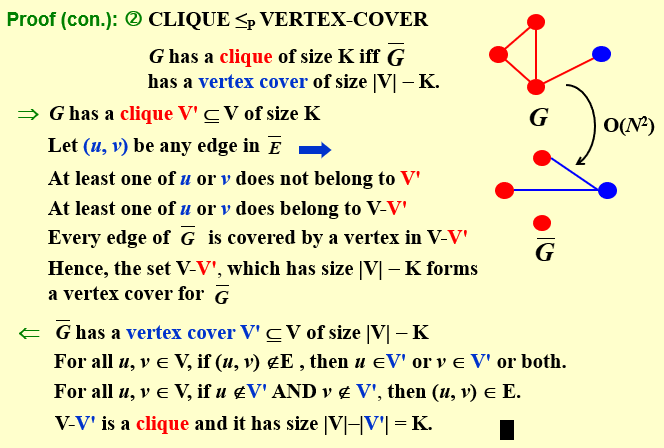
      image-20240611153013922

六、Self-reduction

  1. Self-reduction：一个问题是自归约的，当且仅当这个问题的搜索问题 可以多项式规约到 判定问题
  2. SAT问题是self-reduction的
    1. 对于k-SAT问题：通过任取一个变量xi，将其分别赋值为0和1，得到两个(k-1)-SAT问题，这一步骤是多项式时间的（最多有2n种情况）
    2. 而k-SAT问题 和 (k-1)-SAT问题 都是SAT问题，因此 SAT问题 可以多项式归约到 SAT问题
  3. 所有的NPC问题都是self-reducible

七、例题

  1. 如果\(L_1 \le_p L_2\)并且\(L_2 \in NP\)，则\(L_1\in NP\)
    • 答案：正确
    • 解析：\(P \sube NP\)是一定成立的
  2. 所有NP问题，可以在一个非确定图灵机中，在多项式时间内解决solved
    • 答案：正确
    • 解析：所有NP问题均为判定问题，解决 ==> 判定