ADS11:近似算法
Approximation 近似解
一、Approximation Ratio 近似比
\(\rho(n)\)近似算法 \(\rho(n)-approximation\ algorithm\)
- 设近似解的答案为\(C\),最优解的答案为\(C^*\),则近似算法的近似比\(\rho(n)=max(\frac{C}{C^*},\frac{C*}{C})\)
- 对于任意输入\(I\),近似解为求一个上确界
- 求极小值:\(\alpha=sup(\frac{C(I)}{OPT(I)})\)
- 求极大值:\(\alpha=sup(\frac{OPT(I)}{C(I)})\)
- 一般情况下,\(C(I)\)是可以直接计算出来的,而\(OPT(I)\)需要通过放缩得到一个不等式
\(1+\epsilon\)近似算法 \((1+\epsilon)-approximation\ algorithm\)
- 近似算法的近似比为\(1+\epsilon\)
- 时间复杂度:多项式时间
多项式近似方案 \(polynomial-time\ approximation\ scheme(PTAS)\)
- 给定一个常数\(\epsilon\),算法的近似比为\(1+\epsilon\)
- 时间复杂度:多项式时间,为\(O(n^k)\),k与\(\epsilon\)有关
- 例:\(O(n^{2/\epsilon})\)
完全多项式近似方案 \(fully\ polynomial-time\ approximation\ scheme(FPTAS)\)
- 给定一个常数\(\epsilon\),算法的近似比为\(1+\epsilon\)
- 时间复杂度:多项式时间,为\(O(k*n^\alpha)\),k与\(\epsilon\)有关,\(\alpha\)为常数
- 例:\(O((\frac{1}{\epsilon})^2 n^3)\)
二、Approximate Bin Packing 近似装箱问题
2.1 问题描述
- 给定n个size为\(S_1,S_2,...S_n(0< S_i \le 1)\)的物品,物品不可分割,将这n个物品用最少的箱子装出来,求最少需要多少个箱子
- 是NPC问题
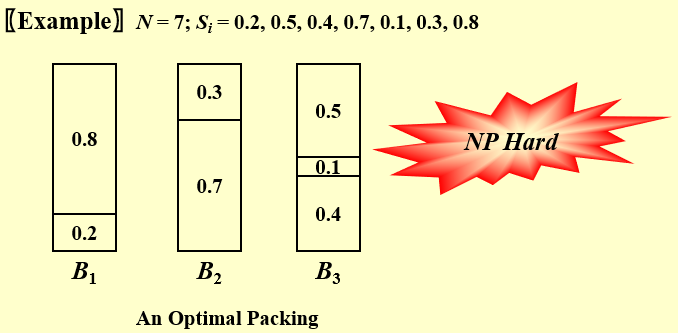
2.2 算法
2.2.1 NextFit:来一个物品,装入当前箱子,装不下去就新开一个箱子
算法:
void NextFit ( ){
read item1;
while (read item2){
if (item2 can be packed in the same bin as item1 )
place item2 in the bin;
else
create a new bin for item2;
item1 = item2;
}
}定理:如果M是最优解,则这个算法的解不超过2M-1
证明:即证,如果NextFit算法使用了2M个箱子,则最优解一定至少使用M+1个箱子
- 在极端情况下,最优解算法求出的每个箱子都是满的,即最优解\(\ge\)所有箱子都是满的情况
- 设\(S(B_i)\)为NextFit算法求出的第i个箱子的大小,则
- \(S(B_1)+S(B_2)>1,\ ...\ ,S(B_{2M-1})+S(B_{2M})>1\)
- \(\therefore \sum_{i=1}^{2M} S(B_i)>M\)
- \(\therefore\) 最优解最少需要\(M+1\)个箱子
近似比为2的例子:
- 物品的大小为\(\frac{1}{2}\)、\(\epsilon\)
- 输入:\(\frac{1}{2}\)、\(\epsilon\)交替输入,共2n组(\(n \rightarrow \inf\))
- 最优解:将\(\frac{1}{2}\)成对放入箱子中,然后将所有\(\epsilon\)放入另一个箱子,共需要n+1个箱子
- NextFit的解:将每一组分别放入一个箱子,共需要2n个箱子
- 近似比:\(\alpha = \frac{2n}{n+1} \rightarrow 2\)
2.2.2 FirstFit:来一个物品,从第一个箱子开始找,找到首个能够装进去的箱子
算法:
void FirstFit ( ){
while(read item){
scan for the first bin that is large enough for item;
//维护一个区间最大值(剩余容量),但是平衡树的key是箱子的编号
if (found)
place item in that bin;
else
create a new bin for item;
}
}定理:如果M是最优解,则FirstFit算法的解不超过\(\frac{17M}{10}\),且存在一种输入,使得近似解为\(\frac{17(M-1)}{10}\)
1.7的例子:\(\frac{1}{6}-\epsilon\)、\(\frac{1}{3}-\epsilon\)、\(\frac{1}{2}+\epsilon\)
- 物品大小为:\(\frac{1}{6}-\epsilon\)、\(\frac{1}{3}-\epsilon\)、\(\frac{1}{2}+\epsilon\)
- 输入:n个\(\frac{1}{6}-\epsilon\)、n个\(\frac{1}{3}-\epsilon\)、n个\(\frac{1}{2}+\epsilon\)
- 最优解:以\(\frac{1}{6}-\epsilon\)、\(\frac{1}{3}-\epsilon\)、\(\frac{1}{2}+\epsilon\)为一组,共需要\(n\)个箱子
- FirstFit的解:\(\frac{n}{6}+\frac{n}{3}+n\)
- 近似比:\(\alpha = \frac{\frac{n}{6}+\frac{n}{3}+n}{n} = \frac{1}{6}+\frac{1}{3}+1=1.5\)
2.2.3 BestFit:来一个物品,找到空余内存最少的箱子,将物品装进去
2.2.4 On-line Algorithm:在线算法
- 在装完上一个物品后,就不能再改变了,且装上一个物品时不知道之后的物品的大小
- 定理:任何一个在线算法的近似比,一定\(\ge\frac{5}{3}\)
- 证明:对手法,对每一种近似算法,找到一组输入,让近似比\(\ge\frac{5}{3}\)
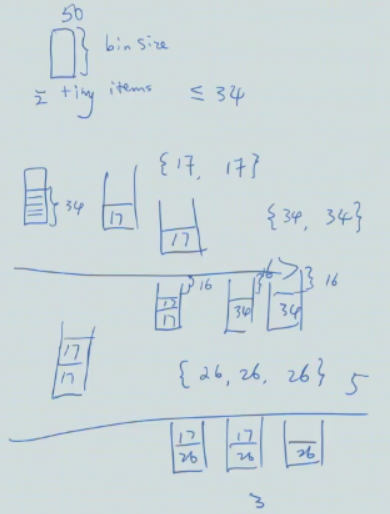
- 假设有34个体积为1的物体,箱子的容量为50
- 如果算法无法将这些物体放到一个箱子里,则近似比\(\ge\frac{5}{3}\)(最优解为1,而该算法的解至少为2)
- 如果可以,则添加2个物体(17,17)
- 如果将这两个17装进2个箱子,则再添加2个物体(34,34),此时近似比\(\ge\frac{5}{3}\)(最优解为3,而该算法的解至少为5)
- 如果将这两个17装进1个箱子,则再添加3个物体(26,26,26),此时近似比\(\ge\frac{5}{3}\)(最优解为3,而该算法的解至少为5)
2.2.6 离线算法
定理:离线算法的近似比,一定\(\ge 1.5\)
三、背包问题
3.1 问题描述
有\(n\)个物体,每个物体有两个属性:体积\(w_i\),价值\(p_i\),选择一部分物体,要求体积和不超过\(M\),且最后的价值和最大
3.2 算法
3.2.1 算法1:优先选择单位价值最大的物体
求解近似比:找一个特例,则近似比不会比这个小
- 假设背包体积为w,有两个物体,一个物体为(\(w=1,p=2\)),另一个物体为(\(w=w,p=w\))
- 最优解:选择(w,w)的物体,总价值为w
- 该算法:选择(1,2)的物体,总价值为2
- 近似比为\(\frac{2}{w}\)
3.2.2 算法2:优先选择价值最大的物体
3.2.3 算法3:选择上述两种算法中,更优的一个解
设\(\frac{p_1}{w_1} \ge \frac{p_2}{w_2} \ge ... \ge \frac{p_n}{w_n}\),根据算法1,装到第\(k\)个时就装不下去了,则
- \(Greedy_1=p_1+p_2+...+p_{k-1}\),算法1会选择1~(k-1)
- \(Greedy_2 \ge p_k\),算法2会从n开始选,直到装不下,至少选择的价值会大于\(p_k\)
可以证明:\(OPT \le p_1+p_2+...+p_{k-1}+p_k=Greedy_1+Greedy_2\)
因此,该算法的近似比为\(\epsilon = \frac{OPT}{max(Greedy_1,Greedy_2)} \le \frac{Greedy_1+Greedy_2}{max(Greedy_1,Greedy_2)} \le 2\)
四、load balancing
4.1 问题描述
有m个人,n个工作,每个工作有一个时间\(p_i\),要求每个人的最大工作时间尽可能小
4.2 算法
求近似比,要先对\(OPT\)进行估计,估计出上界/下界
- \(OPT \ge p_n\),每个人的最大工作时间至少为最长的那个工作
- \(OPT \ge \frac{mx+p_n}{m}=x+\frac{p_n}{m}\)
\(AIG=x+\frac{p_n}{m}+(1-\frac{1}{m})p_m \le OPT+(1-\frac{1}{m})OPT=(2-\frac{1}{m})OPT\)
\(\epsilon \le 2-\frac{1}{m}\)
错题
1 最大生成树

S:每个点的临边中,边权最大的边的集合
T:图的最大生成树
证明C:最大生成树中的每一条边,至少是某一个顶点的最大临边
2 旅行商问题 TSP
TSP问题:找一条路径,经过所有节点至少一遍,最后回到起点,并且使边权和最小
算法:找到图的最小生成树,从起点开始,按照先根/后根/中序遍历,走完整个生成树
近似比:设该算法的答案为\(C\),最优解为\(C^*\),则\(C<C^*<2C\)
- 最优解一定比\(C\)大:因为最小生成树是TSP问题的一个松弛解(要求更低的解)