ADS12:局部搜索
第12章 Local Search
一、定义
Local
- 定义可行解的neighborhoods
- 局部最优解local optimum:在一个neighborhoods中的最优解
Search
- 从一个可行的解决方案开始,在附近寻找一个更好的
- 如果没有改进的可能,则达到局部最优
Local Search 对NP-hard问题很难找到最优解
二、顶点覆盖问题
2.1 算法1:优先选择度最大的顶点
2.2 算法2:任意选一条边,将两个顶点加入集合
近似比为2
- 算法选出的边,都不相交
- 由于都不相交,最优解至少要用一半的顶点完成覆盖
- 因此这个算法的近似比\(\le 2\)
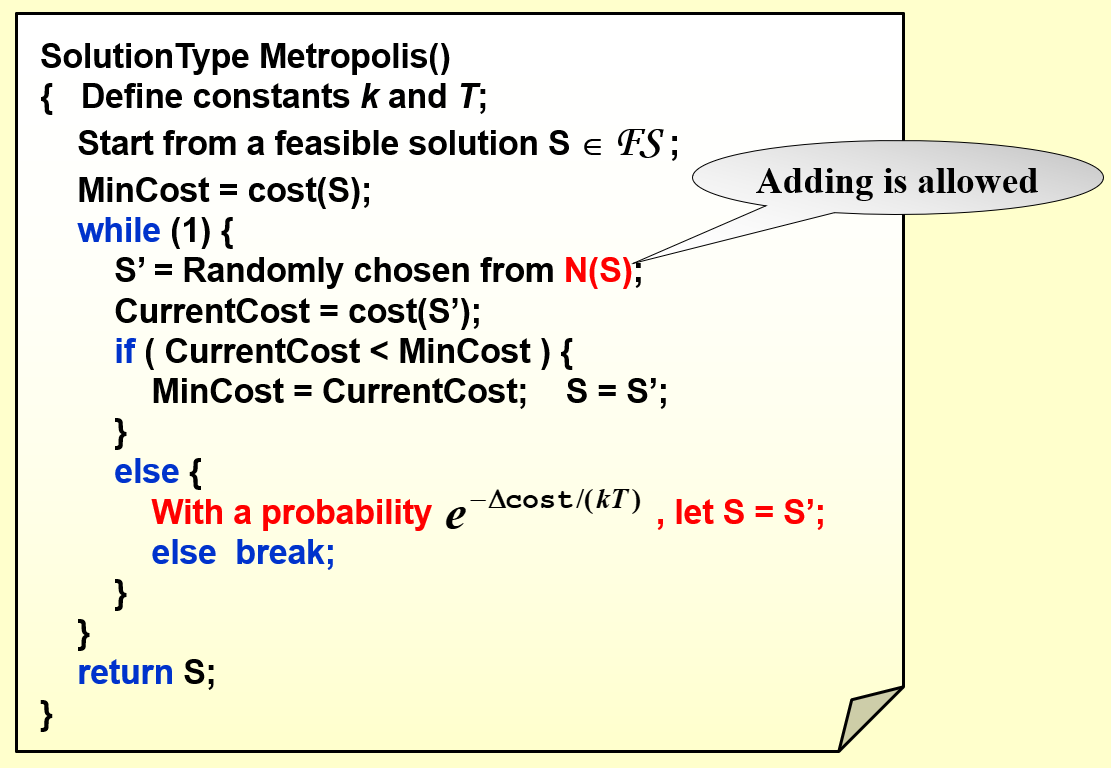
2.3 Metropolis算法
模拟退火
三、Hopfield Neural Networks
3.1 问题描述
设\(G=(V,E)\)
- \(E\)中的每一条边\(e\)有一个权值\(w\),\(w\)可以为正也可以为负。
- \(V\)中的每一个顶点\(v\)可以是正,也可以是负
对于每一个顶点,如果\(\sum_{v:e=(u,v)\in E}w_e s_u s_v \le 0\),则称这个点为\(satisfied\)
对于每一条边\(e=(u,v)\),如果\(w_e s_u s_v < 0\),则称这条边为\(good\)
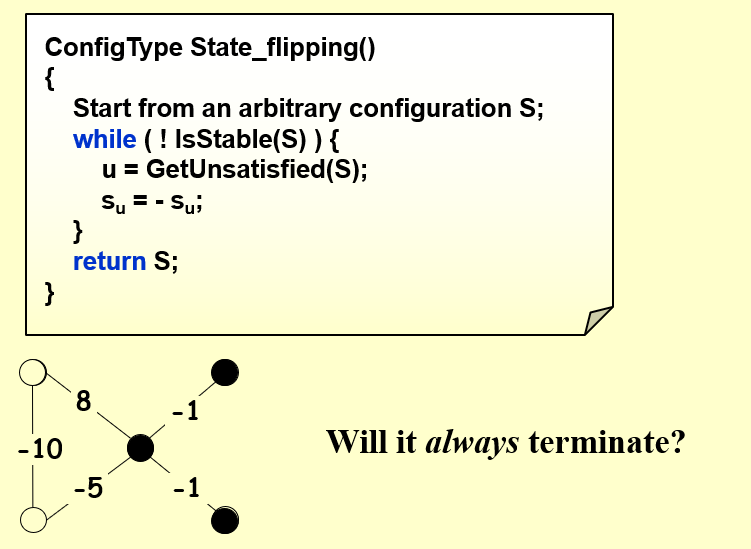
3.2 State-flipping Algorithm
- 从任意一个状态\(S\)出发
- 如果\(S\)不满足条件,则找到\(S\)中任意一个不\(satisified\)的节点u,将节点u的状态取反,并更新\(S\)
- 直到\(S\)满足条件
3.3 定理
- 上述算法一定能够停止在一个稳定的状态
- 最多需要\(W=\sum_e|w_e|\)次迭代
- 设\(\Phi(S)=\sum_{e是good}|w_e|\)
- 每次迭代,u的临边中,原来是good的边变成了bad,原来是bad的边变成了good
- 因此,\(\Phi(S')=\Phi(S)-\sum_{e为u的临边且为bad}|w_e|+\sum_{e为u的临边且为good}|w_e|\)
- 由于每次找的点u是\(unsatisfied\)的,即后面的和$$1
- 因此,\(\Phi(S') \ge \Phi(S)+1\),最多需要\(W=\sum_e|w_e|\)次迭代
3.4 Local Search算法

四、The Maximum Cut Problem 最大割问题
4.1 问题描述
给定一个无向图\(G=(V,E)\),每条边的边权为正数
将所有点分为两部分\((A,B)\),让所有连接\(A,B\)之间的边的边权和最大
\(w(A,B)=\sum_{u \in A, v \in B}w_{uv}\)
4.2 Local Search 算法
- 从\(A\)中选择一个点\(u\),满足 割边的边权和 > 内边的边权和,则将\(u\)放入\(B\)中
- 这样,当状态转换的时候,与\(u\)相连的边的状态会取反(割边变为内边,内边变为割边)
4.3 定理
局部最优解 至少为 全局最优解 的\(\frac{1}{2}\),即:\(w(A,B) \ge \frac{1}{2} w(A^*,B^*)\)
- 由于(A,B)是局部最优解,则对于A中的任意一个点\(u\),与A内的节点相连的边权和\(\le\)与B内的节点相连的边权和\(\sum_{v\in A}w_{uv} \le \sum_{v\in B}w_{uv}\)
- 将上式对所有\(u \in A\)求和得:\(2\sum_{A中的所有边(u,v)}w_{uv} \le \sum_{u\in A}\sum_{v\in B}w_{uv}=w(A,B)\)
- 可得:\(2\sum_{A中的所有边(u,v)}w_{uv} \le w(A,B)\),\(2\sum_{B中的所有边(u,v)}w_{uv} \le w(A,B)\)
- 所以:\(w(A^*,B^*)\le \sum_{A中的所有边(u,v)}w_{uv} + \sum_{B中的所有边(u,v)}w_{uv}\le 2w(A,B)\)


4.4 Big-improvement-flip
- 只有当选出的这个点换到\(B\)中,导致新的答案至少是\(\frac{2\epsilon}{|V|}w(A,B)\)时,才将这个点换过去
- 局部最优解 至少是 全局最优解 的\(\frac{1}{2+\epsilon}\),即:\(w(A,B) \ge \frac{1}{2+\epsilon} w(A^*,B^*)\)
- 最多进行\(O(\frac{n}{\epsilon} \log W)\)次迭代

4.5 K-L heuristic

LKH算法:TSP
课后题:
对于下图中给出的图,如果我们从删除黑色顶点开始,那么局部搜索总是可以找到最小顶点覆盖
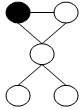
答案:T
在平面上有\(n\)个点\(S=\{s_1,...s_n\}\),我们想要构造一个有\(k\)个中心点的点集\(C=\{c_1,...c_k\}\),使得从所有点到最近的中心点的距离最小。这里\(c_i\)可以是平面中的任意点
一个local search算法会首先任意选择\(k\)个点作为中心点,然后
- 将\(S\)分为\(k\)个集合,\(S_i\)是以\(c_i\)为最近中心点的所有顶点的集合
- 对于每一个\(S_i\),计算出其中心点作为\(S_i\)的新的中心点
如果上述两个步骤导致了覆盖半径严格减少,则进行下一次迭代,否则终止计算
问:当上述局部搜索算法终止时,其解的覆盖半径是否为最优覆盖半径的2倍
答案:F
解析:构造一个反例
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 华风夏韵!
评论