Randomized Algorithms

一、招聘问题 Hiring Problem

1.1 问题描述

每天面试一个不同的面试者，持续\(N\)天

面试一个面试者的代价为\(C_i\)，招聘一个面试者的代价为\(C_h\)

一共招聘\(M\)个面试者，求面试并招聘完所有的面试者所需要的代价

1.2 离线算法

先面试完所有的面试者，然后再选择招聘的人：\(O(NC_i+MC_h)\)

1.3 在线算法

面试一个面试者，然后与之前面试过的面试者进行比较，如果更优，则招聘：\(O(NC_h)\)

1.4 随机算法--离线

假设所有的面试者以一个随机的顺序到来 \[ X_i= \left\{ \begin{aligned} 1 &\ 面试者i被招聘\\ 0 &\ 面试者i没有被招聘 \end{aligned} \right. \] 设\(X\)表示：招聘的人数，则\(X=\sum_{i=1}^N X_i\)

\(E[X_i]=\frac{1}{i}\)

\(E[X]=E[\sum_{i=1}^N X_i]=\sum_{i=1}^N E[X_i]=\sum_{i=1}^N \frac{1}{i}=\ln N+O(1)\)

最后的代价为：\(O(C_h \ln N+NC_i)\)

1.5 随机算法--在线

面试每一个面试者，在面试的时候要立即做决定：

首先观察\(k\)个面试者，找出他们中最优的一位，但是这\(k\)个面试者都不招聘
从第\(k+1\)个面试者开始，如果当前的面试者比之前\(k\)个面试者中最优的面试者好，则直接招聘
如果找不到，则招聘最后一个面试者

int OnlineHiring(EventType C[], int N, int k ){
    int Best = N;
    int BestQ = -INF;
    for (int i=1; i<=k; i++){
        Qi = interview(i);
        if (Qi>BestQ) BestQ = Qi;
    }
    for (int i=k+1; i<=N; i++)
        Qi = interview(i);
        if (Qi>BestQ){
            Best = i;
            break;
        }
    return Best;
}

算法分析：

设\(S_i\)表示：第\(i\)个面试者是最好的

设事件\(A\)表示：最好的面试者在第\(i\)个位置 ==> \(Pr[A]=\frac{1}{N}\)
设事件\(B\)表示：从\((k+1) → (i-1)\)的面试者均没有被招聘，即前\(i-1\)个人中的最大值在前\(k\)个人之中 ==> \(Pr[B]=\frac{k}{i-1}\)
易得，事件\(A\)和事件\(B\)是独立的

则\(Pr[S_i] = Pr[A∩B]=Pr[A]*Pr[B]=\frac{k}{N*(i-1)}\)

\(Pr[S]=\sum_{i=k+1}^{N}Pr[S_i]=\sum_{i=k+1}^{N}\frac{k}{N*(i-1)}=\frac{k}{N}\sum_{i=k}^{N-1}\frac{1}{i}\)

可得：\(\frac{k}{N}ln(\frac{N}{k}) \le Pr[S] \le \frac{k}{N}ln(\frac{N-1}{k-1})\)

二、快排 Quick Sort

算法分析1

\[ X_{ij}= \left\{ \begin{aligned} 1 &\ a_i和a_j进行了比较\\ 0 &\ a_i和a_j没有进行比较 \end{aligned} \right. \]

设\(X=\sum_{j=1}^N\sum_{i=1}^{j}x_{ij}\)，则\(E[X] = \sum_{j=1}^N\sum_i^{j}E[x_{ij}] = \sum_{j=1}^N\sum_{i=1}^{j}Pr[x_{ij}=1]\)
而对于\(Pr[x_{ij}=1]\)，\(a_i\)和\(a_j\)会进行比较，当且仅当：\(a_i\)和\(a_j\)在有且仅有一个子过程中，\(a_i\)或\(a_j\)被选中为\(pivot\)，且\(a_{i+1} → a_{j-1}\)没有被选中为\(pivot\)
由于算法保证每个\(a_i\)被取为\(pivot\)的概率为均等的，因此\(Pr[x_{ij}]=\frac{2}{j-i+1}\)
可得：\(X = \sum_{j=1}^N\sum_{i=1}^{j}\frac{2}{j-i+1} = O(n \log n)\)

算法分析2

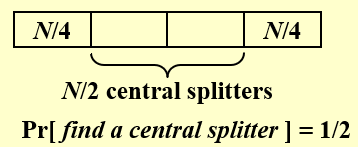
设central splitter：表示可以将n个数分为两边，每一边至少有\(\frac{n}{4}\)个元素的pivot
Modified QuickSort：每一步总是选择central splitter
在每一次选择pivot的时候，选中central splitter的概率为\(p=\frac{1}{2}\)，则选中central splitter的期望次数为\(E=\frac{1}{p}=2\) (几何分布的期望)
Type j：如果\(N(\frac{3}{4})^{j+1} \le |S| \le N(\frac{3}{4})^j\)，则称子问题\(S\)为type j的
定理：最多有\((\frac{4}{3})^{j+1}\)个type j的子问题

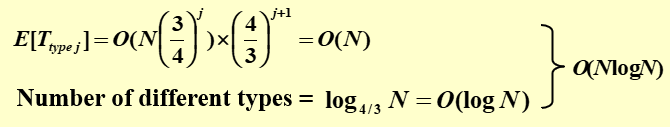
课后题

给定一个有n个节点的链表，我们的任务是删除链表中的所有元素。在每一步中，我们随机的选择当前链表中的一个节点，删除它及它之后的所有节点。假设我们每一次选择节点都是在剩下的节点中等概率的选取一个点，则我们期望需要多少步能够删除完所有的节点
- 答案：\(O(\log N)\)
- 设需要\(T(N)\)步，则\(T(N)=\frac{1}{N}(T(1)+T(2)+...+T(N-1))+1\)
在在线招聘算法中，\(C[i]\)的权值是平均的。若\(N=271,k=90\)，则选中第\(N\)个求职者的概率为
- 答案：\(\frac{1}{3}\)
- 如果要雇佣第271个，则要求前270个中，最好的必须要落在前k个，因此，概率为\(\frac{90}{270}=\frac{1}{3}\)