ADS14:并行算法
Parallel Algorithms
一、并行算法的描述
1.1 PRAM:Parallel Random Access Machine
机器资源有多少,就算多少
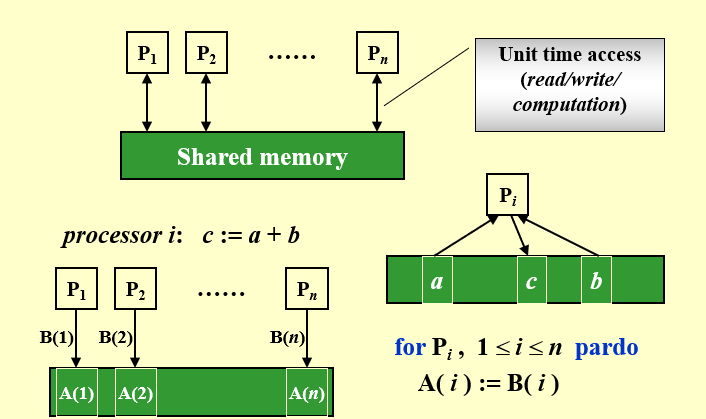
解决访问冲突:
- EREW:Exclusive-Read Exclusive-Write
- CREW:Concurrent-Read Exclusive-Write
- CRCW:Concurrent-Read Concurrent-Write
- Arbitrary rule:随机写
- Priority rule (P with the smallest number):根据优先级判断
- Common rule (if all the processors are trying to write the same value):将相同的运算并行计算
1.2 WD:Work-Depth
只计算真正被调用的资源
- Work:真正被调用的核
- Depth:并行算法消耗的时间
1.3 衡量指标
- Work Load:W(n),总计操作数
- Worst-case Running Time:T(n)
- 有W(n)个操作,T(n)的时间
- P(n) = W(n)/T(n) processors and T(n) time (on a PRAM)
- W(n)/p time using any number of p ≤ W(n)/T(n) processors (on a PRAM)
- W(n)/p + T(n) time using any number of p processors (on a PRAM)
二、求和问题
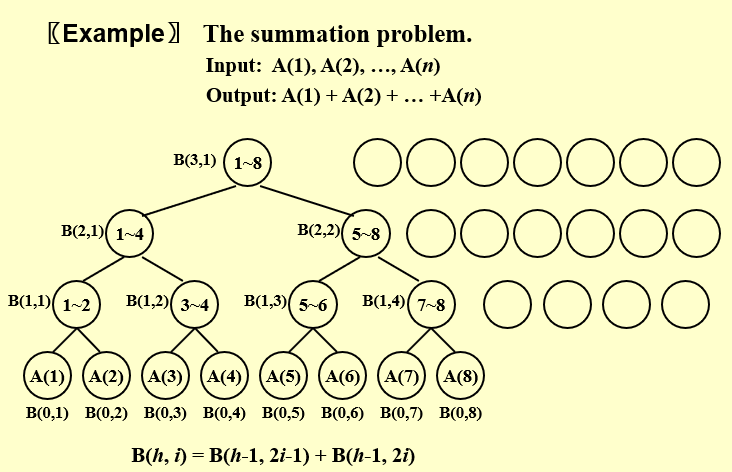
2.1 PRAM model

- 随着时间的推移,有很多核没有被使用
2.2 Work-Depth Presentation
计算过程:
- 并行运算:\(B(0,i)=A(i)\)
- \(h\)从\(1 \rightarrow \log n\),并行运算:\(B(h,i)=B(h-1,2i-1)+B(h-1,2i)\)
- 并行运算:输出\(B(\log n,1)\)
 \[
\begin{aligned}
T(n)&=1+\log n+1=\log n+2 \\
W(n)&=n+\frac{n}{2}+\frac{n}{2^2}+...+\frac{n}{2^k}+1=2n
\end{aligned}
\]
\[
\begin{aligned}
T(n)&=1+\log n+1=\log n+2 \\
W(n)&=n+\frac{n}{2}+\frac{n}{2^2}+...+\frac{n}{2^k}+1=2n
\end{aligned}
\]
2.3 WD-presentation充分性定理
WD模式下的算法可以由任意P(n)处理器在\(O(\frac{W(n)}{P(n)} + T(n))\)时间内实现,使用与WD表示相同的并发写入约定。
三、前缀和 Prefix-Sums
3.1 问题描述
输入:A(1),A(2),……,A(n)
输出:\(\sum_{i=1}^1 A(i)\),\(\sum_{i=1}^2 A(i)\)n,……,\(\sum_{i=1}^n A(i)\)
3.2 工具:平衡二叉树
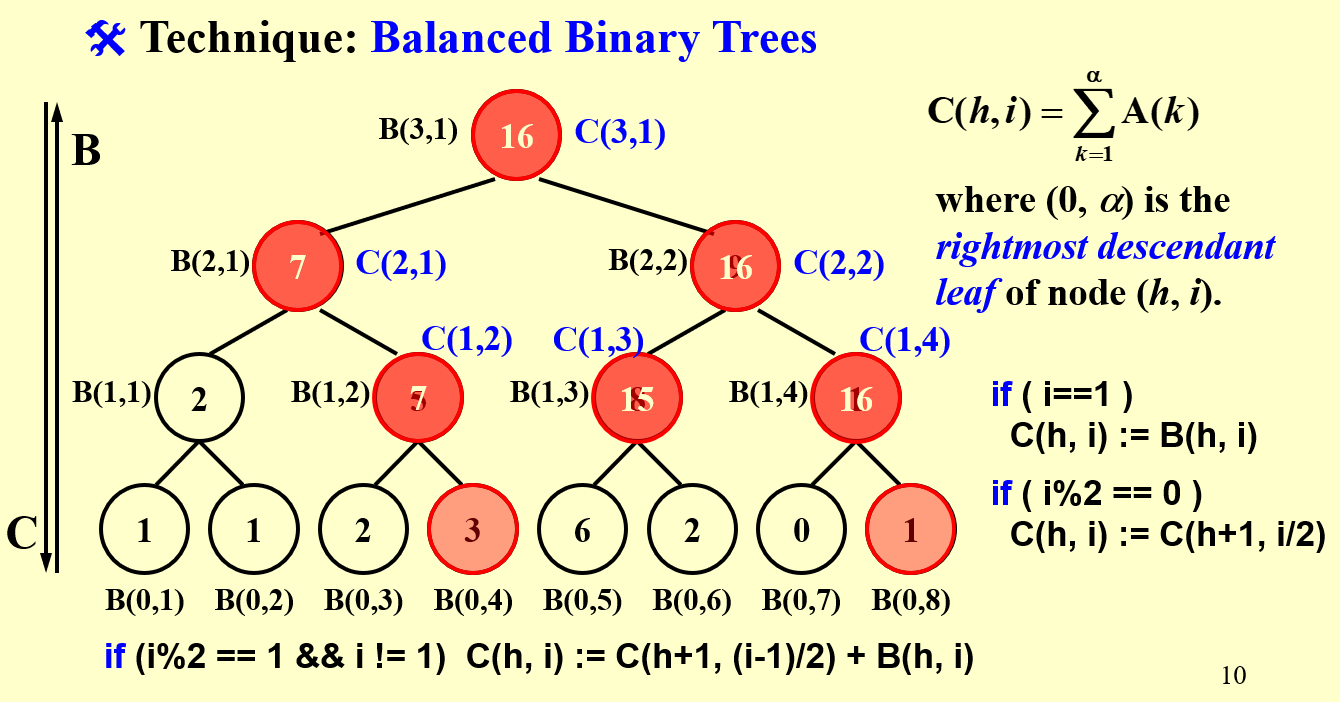
C(h,i)表示:第h层前i个元素的前缀和,从最高层向低层计算 \[ C(h,i)= \begin{cases} C(h+1,i/2) &i是偶数\\ C(h+1,(i-1)/2)+B(h,i) &i是奇数 \end{cases} \]
\[ \begin{aligned} T(n)&=T(\frac{n}{2})+O(1)=O(\log n) \\ W(n)&=W(\frac{n}{2})+n=O(n) \end{aligned} \]
计算过程:
- 执行一遍求和问题的操作,得到所有\(B(h,i)\)
- \(T(n)=\log n+2\)
- \(W(n)=2n\)
- \(h\)从\(\log n \rightarrow 0\),并行运算
- \(i\)为\(1\rightarrow \frac{n}{2^h}\)中的偶数:\(C(h,i)=C(h+1,\frac{i}{2})\)
- \(i\)为\(1\):\(C(h,i)=B(h,i)\)
- \(i\)为\(3\rightarrow \frac{n}{2^h}\)中的奇数:\(C(h,i)=C(h+1,\frac{i-1}{2})+B(h,i)\)
- 并行运算:输出\(C(0,i)\)

四、归并排序
4.1 主要思想
使用并行算法,将Merge的过程的时间复杂度降下来
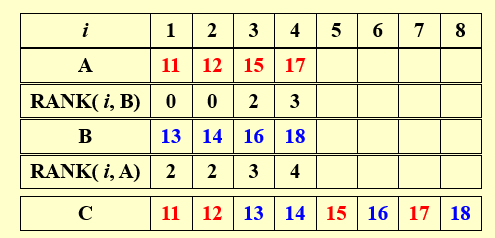
4.2 基础算法:将Merge转为Rank
设Merge时,两个数组分别为\(A_1,A_2...A_n\)和\(B_1,B_2,...B_n\)
将Merge的过程转变为Rank的过程
找到\(A_1,...A_n\)分别在\(B_1,...B_n\)的位置,\(B_1,...B_n\)分别在\(A_1,...A_n\)的位置
对每一个数\(A_i\)或\(B_i\),使用二分查找
并行计算所有的\(A_i\)和\(B_i\),得到\(Rank(i,B),Rank(i,A)\)
\(T(n)=O(\log n)\)
\(W(n)=O(n \log n)\)

根据Rank的值,将\(A_1,A_2...A_n\)和\(B_1,B_2,...B_n\)并行放入结果数组\(C_1,...C_{2n}\)中
- \(A_i\)在\(C\)中的位置:\(Pos=i+Rank(i,B)\)
- \(B_i\)在\(C\)中的位置:\(Pos=i+Rank(i,A)\)
- \(T(n)=O(1)\)
- \(W(n)=O(n)\)

- 总的\(T(n)\)与\(W(n)\):
- \(T(n)=O(\log n)\)
- \(W(n)=O(n \log n)\)
4.3 优化求解Rank的过程:使用\(\log n\)将数组分块,分为\(p=\frac{n}{\log n}\)块
对并行使用二分查找的优化:
- 分块Partitioning,块数\(p=\frac{n}{\log n}\)
- 从\(A\)数组中,选出的第\(i\)个数\(A[i]\)为\(A[1+(i-1)\log n]\),\(1\le i \le p\)
- 从\(B\)数组中,选出的第\(i\)个数\(B[i]\)为\(B[1+(i-1)\log n]\),\(1\le i \le p\)
- 使用二分查找,找到选出的数对应在另一个数组中的位置
- \(T(n)=O(\log n)\)
- \(W(n)=O(p\log n)=O(n)\)
- 计算每个数的Ranking
- 根据\(A[i]\)、\(B[i]\)分别的rank,我们可以将两个数组分成至多\(2p\)块,每块的大小为\(O(\log n)\),且每个块之间相互独立
- 这样,我们就将问题划分成了\(2p\)个大小为\(O(\log n)\)的子问题
- 并行运算:对每个大小为\(O(\log n)\)的块执行归并操作
- \(T(n)=O(\log n)\)
- \(W(n)=O(p\log n)=O(n)\)

五、找最大值
5.1 基础算法:比较所有的pair
并行运算:对任意两个数\(A_i\)和\(A_j\),如果\(A_i<A_j\),则将\(B_i\)赋值为1
- 由于只可能将\(B_i\)从0赋值为1,因此可以忽略冲突
- \(T(n)=O(1)\)
- \(W(n)=O(n^2)\)

5.2 优化:使用\(\sqrt n\)将n个数字分块,分为\(\sqrt n\)块
- 并行运算:对于每一个大小为\(\sqrt
n\)的块,递归计算出最大值
- 计算块\(M_i\)的开销为:\(T(\sqrt n),W(\sqrt n)\)
- 一共需要并行计算\(\sqrt n\)个块
- 对于\(\sqrt n\)个块找出的\(\sqrt
n\)个最大值,使用5.1的算法,找出最大值
- \(T(n)=O(1)\)
- \(W(n)=O(\sqrt n^2)=O(n)\)
- 总的开销为
- \(T(n)=T(\sqrt n)+O(1)=O(\log \log n)\)
- \(W(n)=\sqrt n W(\sqrt n)+O(n)=O(n\log \log n)\)
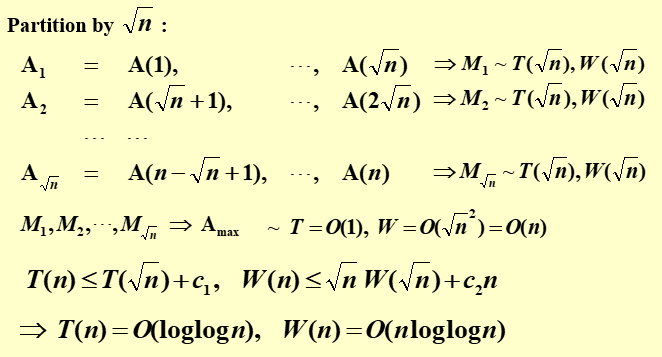
5.3 优化:使用\(h=\log \log n\)将n个数组分块,分为\(\frac{n}{h}\)块
- 并行运算:对于每一个大小为\(h=\log \log
n\)的块,顺序遍历计算出最大值
- \(T(n)=O(h)=O(\log \log n)\)
- \(W(n)=O(h*\frac{n}{h})=O(n)\)
- 对于\(\frac{n}{h}\)个块找出的\(\frac{n}{h}\)个最大值,使用5.2的算法,找出最大值
- \(T(n)=O(\log \log \frac{n}{h})\)
- \(W(n)=O(\frac{n}{h}*\log \log \frac{n}{h})=O(n)\)
- 总的开销为
- \(T(n)=O(h+\log \log \frac{n}{h})=O(\log \log n)\)
- \(W(n)=O(h*\frac{n}{h}+\frac{n}{h}*\log \log \frac{n}{h})=O(n)\)
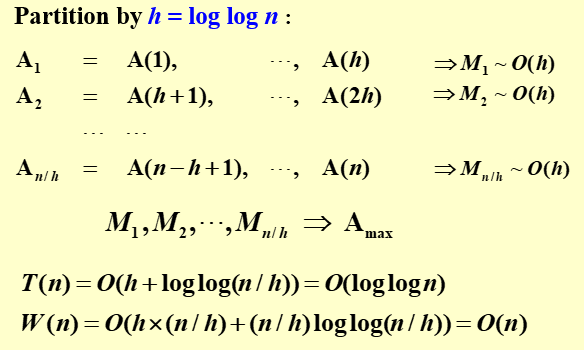
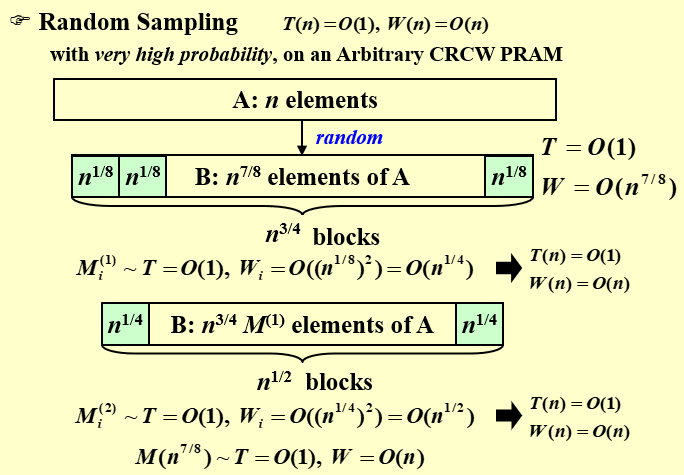
5.4 Random Sampling
- 从A数组中,随机选出\(n^{\frac{7}{8}}\)个元素,组成B数组
- \(T=O(1)\)
- \(W=O(n^{\frac{7}{8}})\)
- 将B数组按照\(n^{\frac{1}{8}}\)分块分为\(n^{\frac{3}{4}}\)块,每一块使用5.1的算法计算最大值
- \(T(n)=O(1)\)
- \(W=(n^\frac{3}{4}) * O((n^{\frac{1}{8}})^2)=(n^\frac{3}{4}) * O(n^{\frac{1}{4}})=O(n)\)
- 对于第2步算出的\(n^{\frac{3}{4}}\)个元素,按照\(n^{\frac{1}{4}}\)分块分为\(n^{\frac{1}{2}}\)块,每一块使用5.1的算法计算最大值
- \(T(n)=O(1)\)
- \(W=(n^\frac{1}{2}) * O((n^{\frac{1}{4}})^2)=(n^\frac{1}{2}) * O(n^{\frac{1}{2}})=O(n)\)
- 总的开销为
- \(T(n)=O(1)\)
- \(W(n)=O(n)\)