ADS15：外排

ExternalSorting 外排

一、总体思想

Run：将内存中的数据排序

Pass：将内存中的数据导入硬盘 / 从硬盘中读入数据到内存

1. 将硬盘中的数据依次读入内存，然后进行排序，写入到2个不同的磁带中
2. 将2个磁带的内容进行合并，写入到另外2个不同的磁带中
3. 重复2，直到排序完成
4. 一共需要至少4个磁带，Pass的次数：\(1+\lceil \log_2(\frac{N}{M})\rceil\)

优化目标

1. 减少Pass的次数

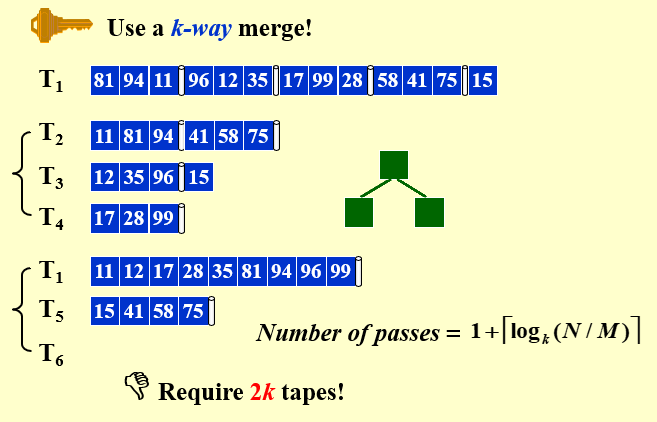
二、k-way合并

1. 将硬盘中的数据依次读入内存，然后进行排序，写入到k个不同的磁带中
2. 将k个磁带的内容进行合并，写入到另外k个不同的磁带中
3. 重复2，直到排序完成
4. 一共需要至少2k个磁带，Pass的次数：\(1+\lceil \log_k(\frac{N}{M})\rceil\)

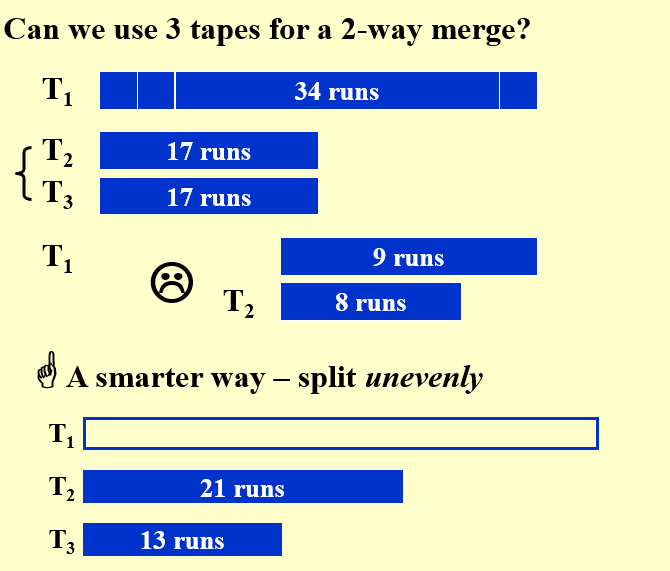
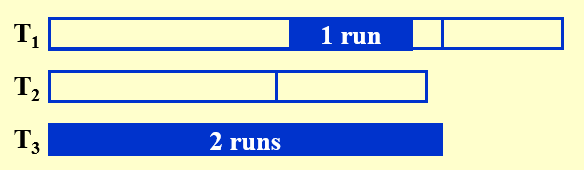
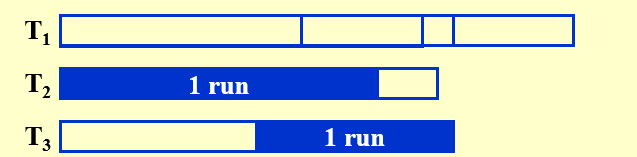
三、使用3个tape实现2-way合并

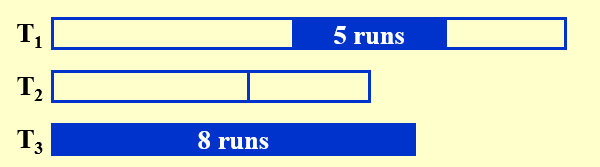
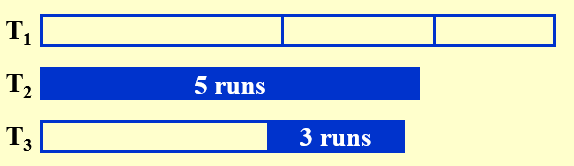
1. 按照斐波那契数列，将排序后的数据不平均的分给其余2个磁带\(F_n=F_{n-1}+F_{n-2}\)
2. 2个磁带合并时，将前\(F_{n-2}\)个数合并，放到空余的1个磁带，此时变成了\(F_{n-1}\)与\(F_{n-2}\)
3. 重复第2步

四、使用k+1个tape实现k-way合并

以3-way合并为例

1. 按照斐波那契数列，将排序后的数据不平均的分给其余3个磁带，此时3个磁带分别为
   1. \(F_{n-1}+F_{n-2}+F_{n-3}\)
   2. \(F_{n-1}+F_{n-2}\)
   3. \(F_{n-1}\)
   4. 原有的数据个数为：\(t_n=3F_{n-1}+2F_{n-2}+F_{n-3}\)
2. 3个磁带合并时，将前\(F_{n-1}\)个数合并，放到空余的1个磁带，此时3个磁带分别为
   1. \(F_{n-2}+F_{n-3}+F_{n-4}\)（上一步产生的\(F_{n-1}\)分解为三项：\(F_{n-2}+F_{n-3}+F_{n-4}\)）
   2. \(F_{n-2}+F_{n-3}\)
   3. \(F_{n-2}\)
3. 重复第2步

五、处理Run时长度超过内存的大小

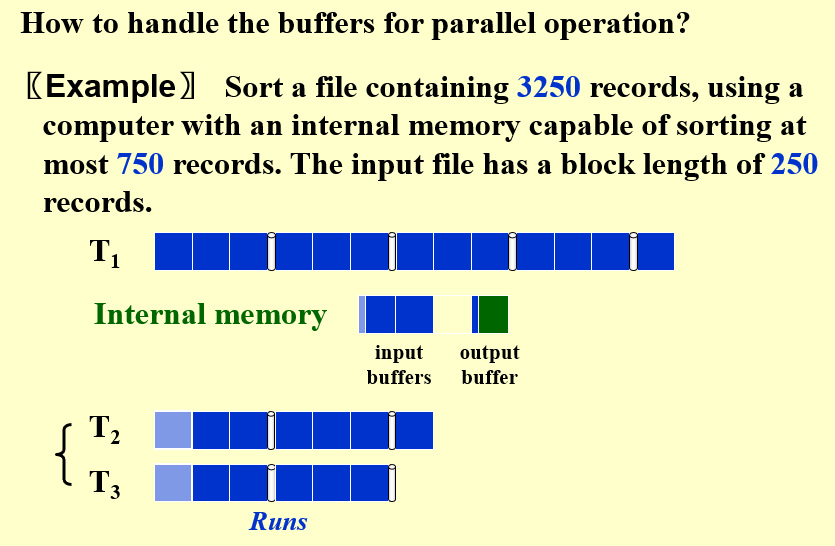
5.1 input buffer和output buffer

1. 将内存分为input buffer和output buffer
2. 每一次比较，将结果放入output buffer
3. 当output bufer满时，将其输出到内存

5.2 对于k-way的合并

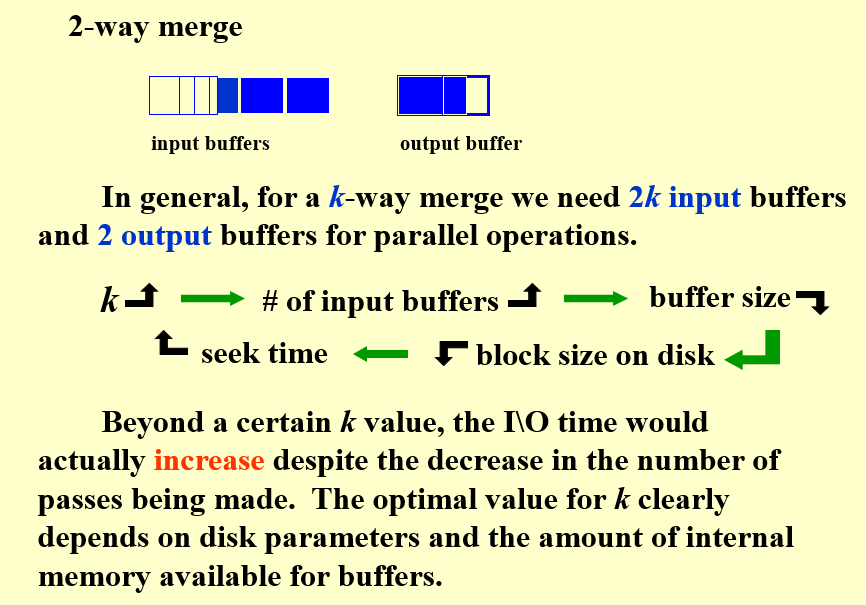
1. 通常情况下，执行k-way合并需要2k个input buffer和2个output buffer
2. 当k变大但内存不变时，需要的input buffer数目上升，因此每个buffer的大小降低，从而导致硬盘中每个block的大小降低，从而导致seek的时间增加
3. 当超过某个k值后，尽管传递次数减少，但IO时间实际上会增加
4. k的最佳值显然取决于磁盘参数和缓冲区可用的内部内存量。

5.3 产生一个长的Run

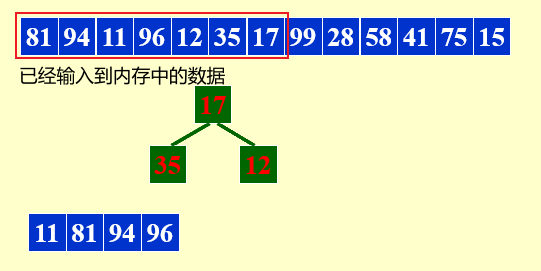
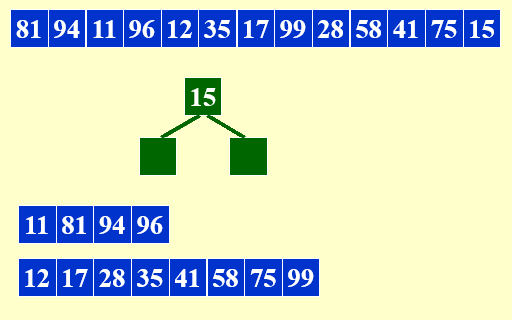
1. 假设内存中只能存放3个数据
2. 将input tape中前3个数据输入内存中
3. 将内存中的最小数据输出到一条新的output tape中，并且从input tape中输入1个数据到内存中
4. 将内存中\(\ge\)上一个输出的数据 的 最小数据，输出到上一次的output tape中，并且从input tape中输入1个数据到内存中
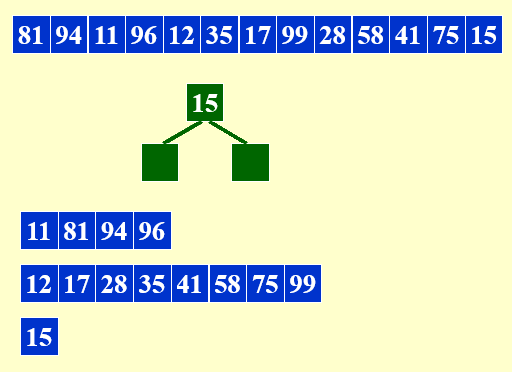
5. 如果内存中的所有数据均比上一次输出的数小，则换一条新的output tape进行输出

在这种替换策略下，每一个run的平均长度为：L=2M

1. 其中M为内存能够容纳的数据的个数

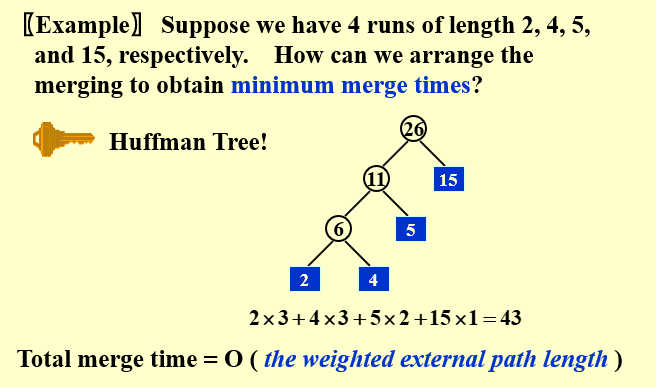
5.4 使用Huffman Tree减少Merge的时间

如果run的长度不一样，怎样减小merge的时间：使用Huffman Tree