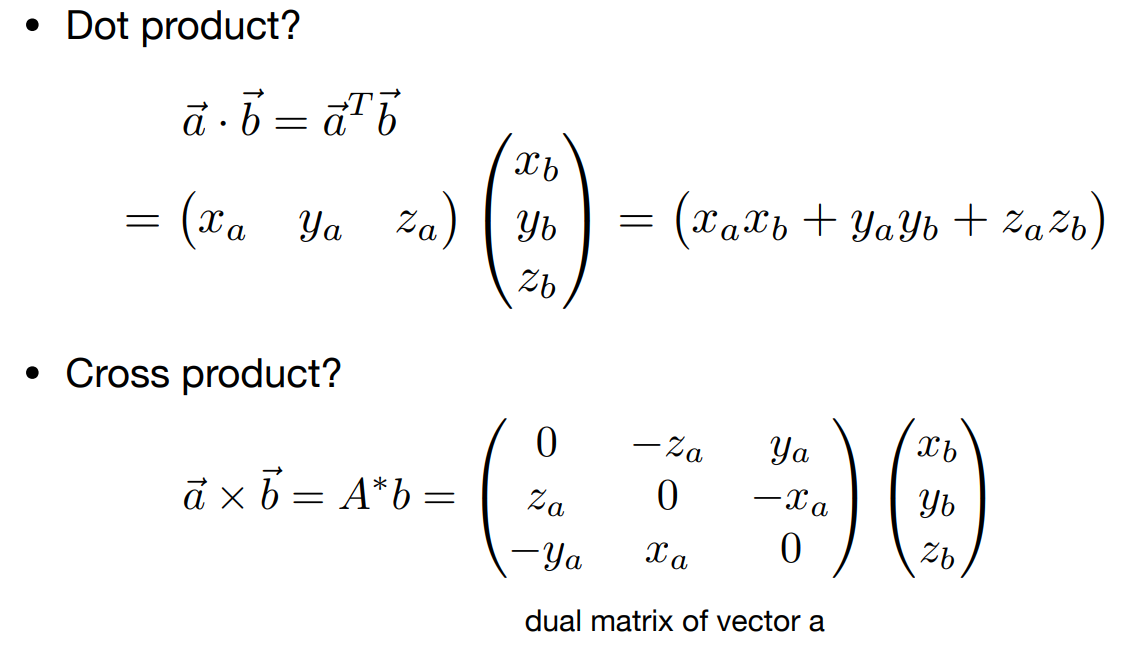二、线性代数复习

2.1 向量点乘

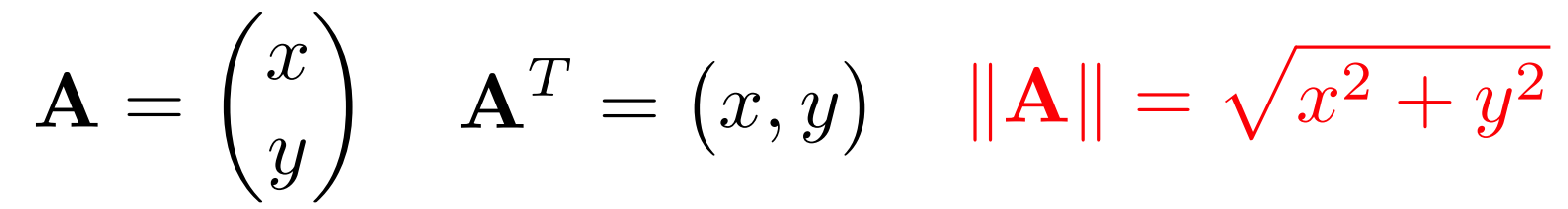
image-20230223163818522

2.1.1 定义

\[ \begin{aligned} \vec{a}·\vec{b}&=||\vec{a}||*||\vec{b}||*\cos\theta \\ &=x_a*x_b+y_a*y_b+z_a*z_b\\ \end{aligned} \]

2.1.2 性质

  1. \(\vec{a}·\vec{b}=\vec{b}·\vec{a}\)
  2. \(\vec{a}·(\vec{b}+\vec{c})=\vec{a}·\vec{b}+\vec{a}·\vec{c}\)
  3. \((k\vec{a})·\vec{b}=\vec{a}·(k\vec{b})=k(\vec{a}·\vec{b})\)

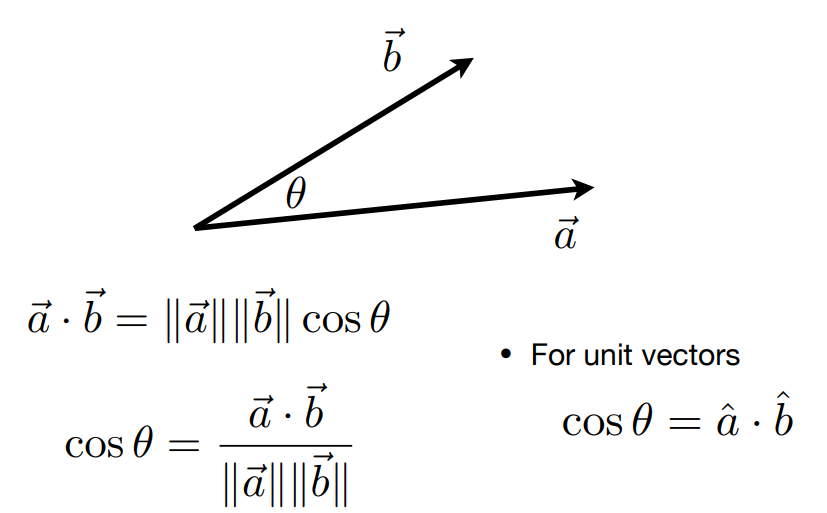
2.1.3 应用

  1. 计算夹角：\(\cos\theta=\frac{\vec{a}·\vec{b}}{||\vec{a}||*||\vec{b}||}\)

    image-20220810170049692

  2. 计算投影：\(||\vec{b}_⊥||=||\vec{b}||\cos\theta\)，\(\vec{b}_⊥=(||\vec{b}||\cos\theta)\ \hat a\)

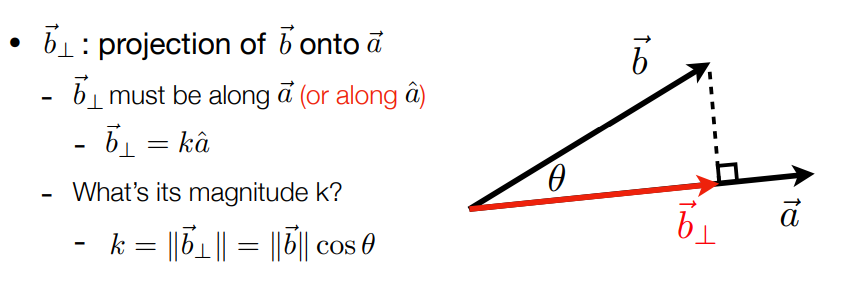
    image-20220810170106422

  3. 将\(\vec{b}\)在\(\vec{a}\)方向分解：\(\vec{b}=\vec{b}_⊥+(\vec{b}-\vec{b}_⊥)\)

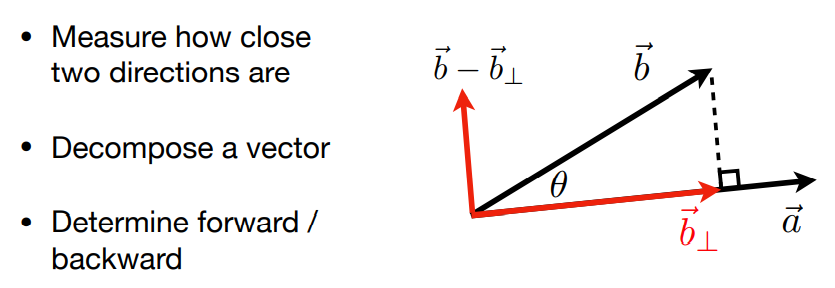
    image-20220810170343996

  4. 向量之间的方向

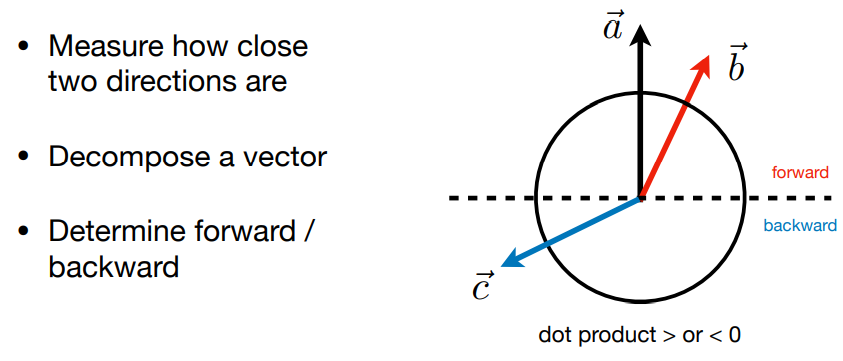
    1. \(\vec{a}\)与\(\vec{b}\)方向基本一致：\(\hat{a}·\hat{b} > 0\)，越接近1，夹角越接近0°
    2. \(\vec{a}\)与\(\vec{b}\)方向基本相反：\(\hat{a}·\hat{b} < 0\)，越接近-1，夹角越接近180°
    3. \(\vec{a}\)与\(\vec{b}\)垂直：\(\hat{a}·\hat{b}=0\)

    image-20220810170534209

2.2 向量叉乘

2.2.1 定义

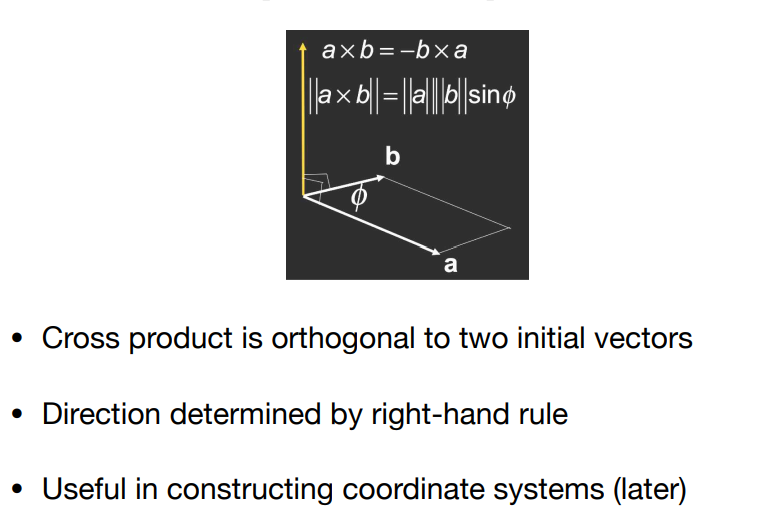
image-20220810171343721

大小：\(||\vec{a}×\vec{b}||=||\vec{a}||*||\vec{b}||*\sin\theta\)

方向：右手螺旋定则，四指方向为\(\vec{a}\)旋转到\(\vec{b}\)，拇指方向为\(\vec{a}×\vec{b}\)的方向

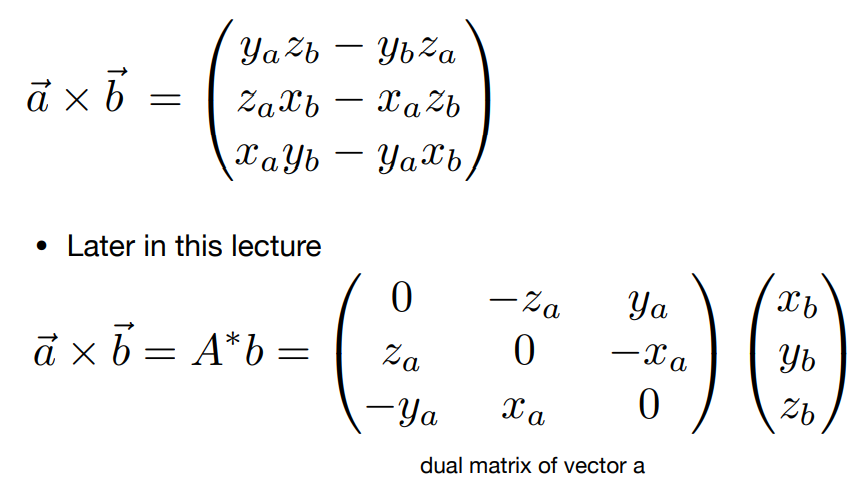
image-20220810172156875

2.2.2 性质

性质：\(\vec{a}×\vec{b}=-\vec{b}×\vec{a}\)，可以用于建立空间直角坐标系：

  1. 右手坐标系：\(\vec{x}×\vec{y}=\vec{z}\)
  2. 左手坐标系：\(\vec{x}×\vec{y}=-\vec{z}\)

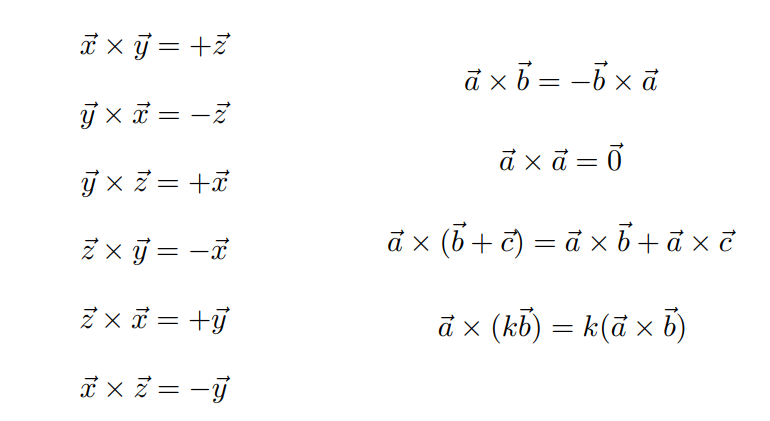
image-20220810171901046

2.2.3 应用

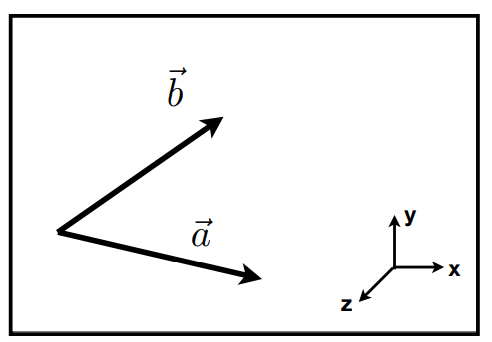
  1. 判断左右：假设\(\vec{a}、\vec{b}\)均在XY平面上

    1. \(\vec{b}\)在\(\vec{a}\)的左侧：\(Z_{\vec{a}×\vec{b}}>0\)
    2. \(\vec{b}\)在\(\vec{a}\)的右侧：\(Z_{\vec{a}×\vec{b}}<0\)

    image-20220810172421848

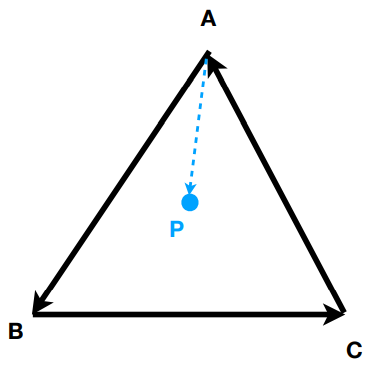
  2. 判断内外：假设ABCP四点共面

    1. P在▲ABC的内部：若ABC逆时针排列，则都在左面；若ABC顺时针排列，则都在右面
      1. \(\vec{AP}\)在\(\vec{AB}\)的左面
      2. \(\vec{BP}\)在\(\vec{BC}\)的左面
      3. \(\vec{CP}\)在\(\vec{CA}\)的左面
    2. P在▲ABC的外部：上述三个条件有一个不符合

    image-20220810172608646

2.3 正交基/坐标系

正交基：Orthonormal Bases

坐标系：Coordinate Frames

2.3.1 定义

  1. \(\vec{u}、\vec{v}、\vec{w}\)均为单位向量
  2. \(\vec{u}、\vec{v}、\vec{w}\)两两垂直
  3. \(\vec{w}=\vec{u}×\vec{v}\)

image-20220810173601736

2.4 矩阵

2.4.1 矩阵乘法

  1. 定义：设\(A[m][n]*B[n][p]=C[m][p]\)，则\(C[i][j]=\sum_{k=1}^n A[i][k]*B[k][j]=\{A的第i行\}·\{B的第j列\}\)
  2. 性质：
    1. 没有交换律
    2. 有结合律：\((AB)C=A(BC)\)
    3. 有分配律：\(A(B+C)=AB+AC\)，\((A+B)C=AC+BC\)

2.4.2 矩阵转置

  1. 定义：将行列互换

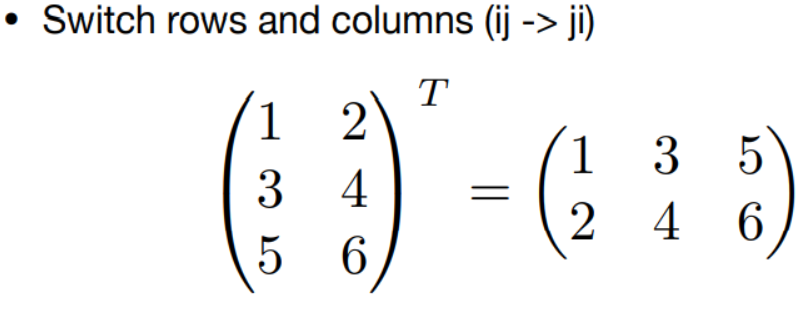
    image-20220812181413411

  2. 性质：\((AB)^T=B^TA^T\)

2.4.3 单位矩阵&矩阵的逆

  1. 单位矩阵：

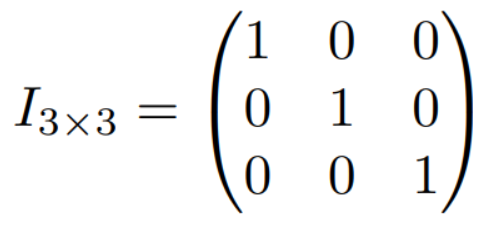
    image-20220812181521742

  2. 逆矩阵的定义：\(AA^{-1}=A^{-1}A=I\)

  3. 逆矩阵的性质：\((AB)^{-1}=B^{-1}A^{-1}\)

2.4.4 矩阵&向量点乘/叉乘

  1. 向量的对偶矩阵：

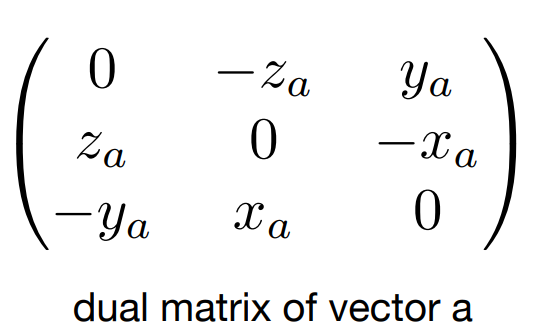
    image-20230223174941145

  2. 矩阵&向量点乘/叉乘：

    image-20230223175008749