三、变换1：2维变换

变换：

  1. Modeling：模型变换，物体在3D空间中的运动
  2. Viewing：视图变换，3D到2D的投影

3.1 2D Transform

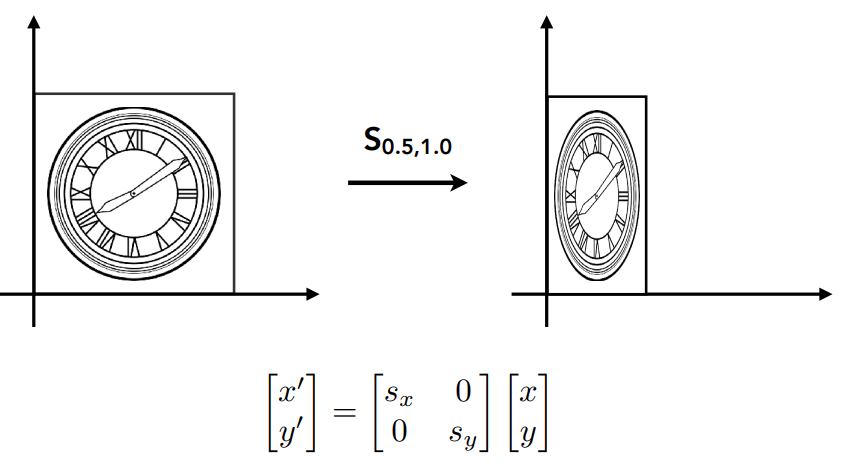
3.1.1 Scale缩放变换

image-20220811125108799

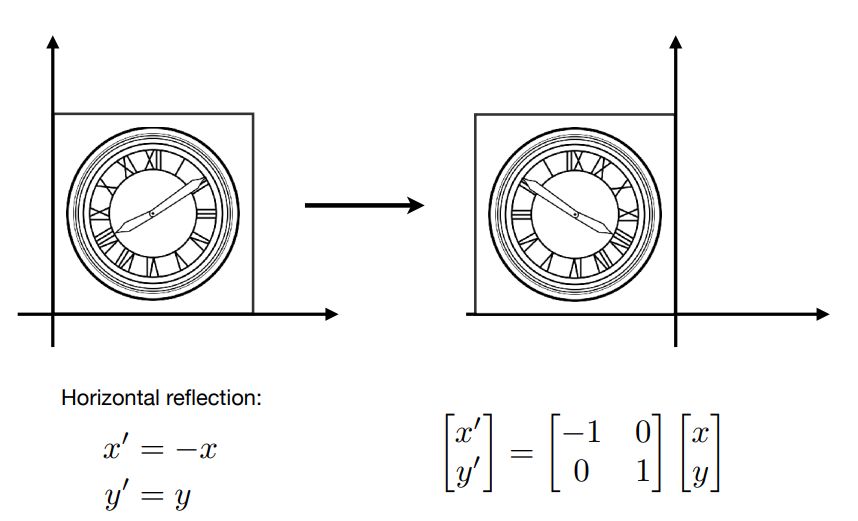
3.1.2 Reflectin翻转

image-20220811125051816

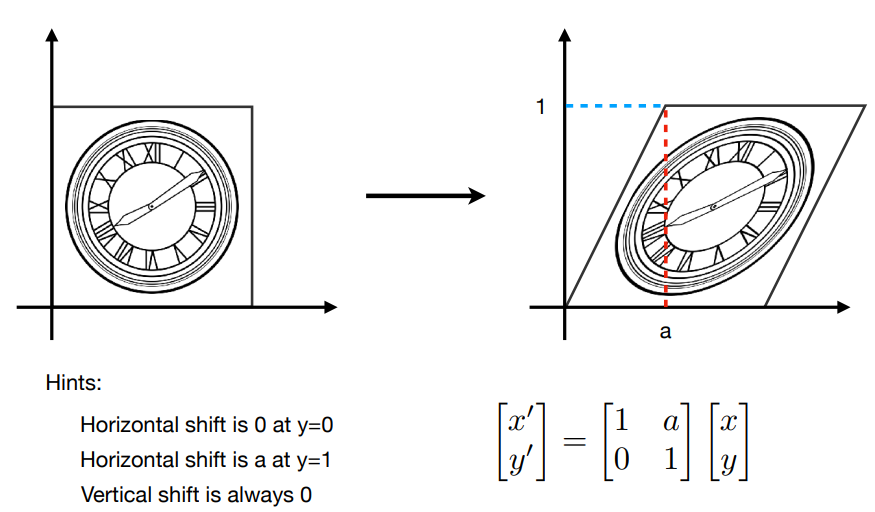
3.1.3 Shear切变

image-20220811125253629

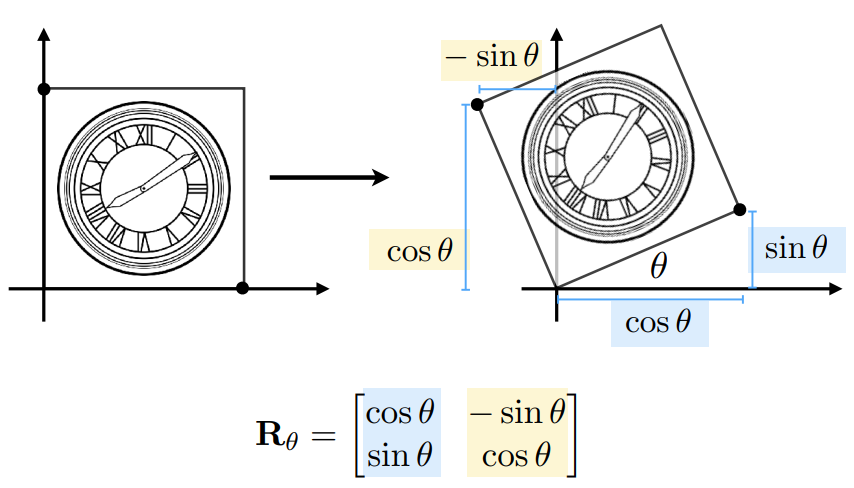
3.1.4 Rotate旋转(默认 绕原点 逆时针 旋转)

image-20220811125758262

3.1.5 Linear Transform线性变换=矩阵

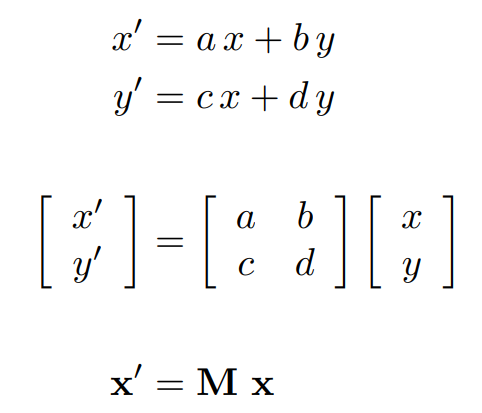
image-20220811130400053

3.2 Homogeneous coordinates齐次坐标

3.2.1 Translation平移变换\(\notin\)线性变换

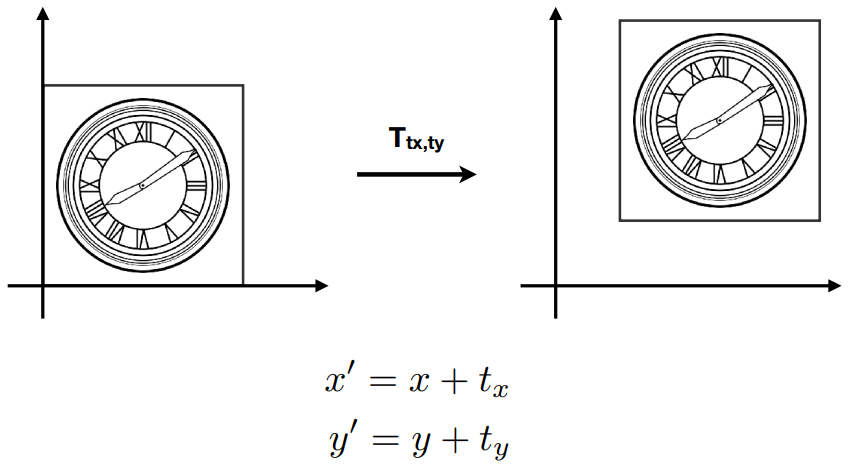
image-20220811130553973

矩阵表示：

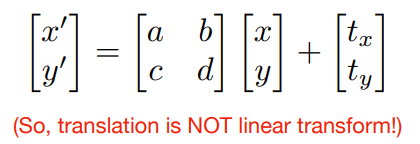
image-20220811130633298

3.2.2 齐次坐标

添加一个维度

  1. 2维点：\((x,y,1)^T\)
  2. 2维点的补充形式：\((x,y,w)^T\)与\((\frac{x}{w},\frac{y}{w},1)^T\)等价
  3. 2维向量：\((x,y,0)^T\)

对于两者第3个坐标的解释：

  1. 点的第三维为0，向量的第三维为1，可以满足向量的平移不变性
  2. 且可以满足以下性质
    1. vector + vector = vector
    2. point - point = vector
    3. point + vector = point
    4. point + point = 两个point的中点

3.2.3 Affine Transformation仿射变换 = 线性变换 + 平移变换

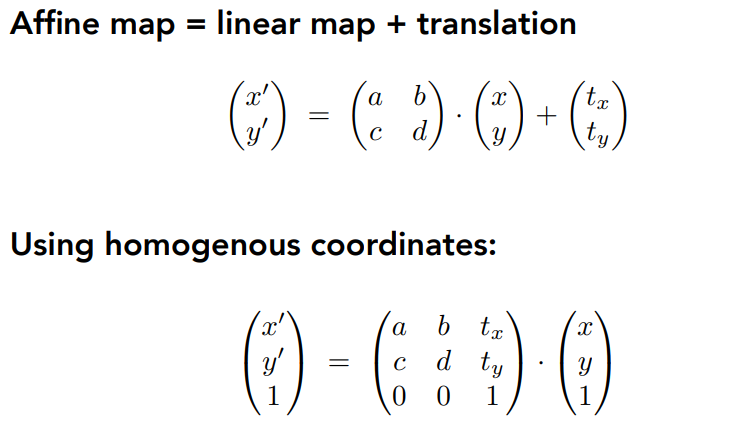
image-20220811131633578

3.2.4 2D Transformation

image-20220811131725685

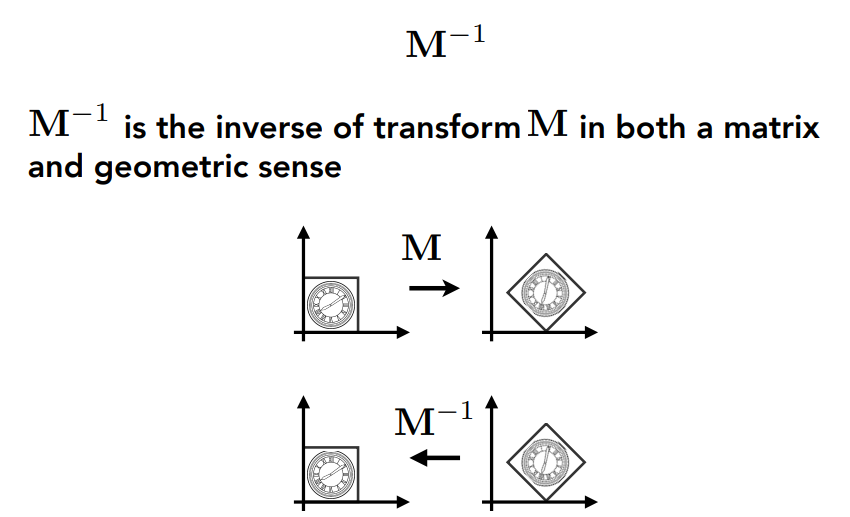
3.2.5 Inverse Transform逆变换

逆变换 <==> 乘变换矩阵的逆矩阵

image-20220811155155659

3.3 Composing Transforms变换的组合

3.3.1 举例

  1. 复杂变换可以有简单变换组合而成
  2. 简单变换的顺序是很有必要的 <==> 矩阵乘法不满足交换律

变换的目标：

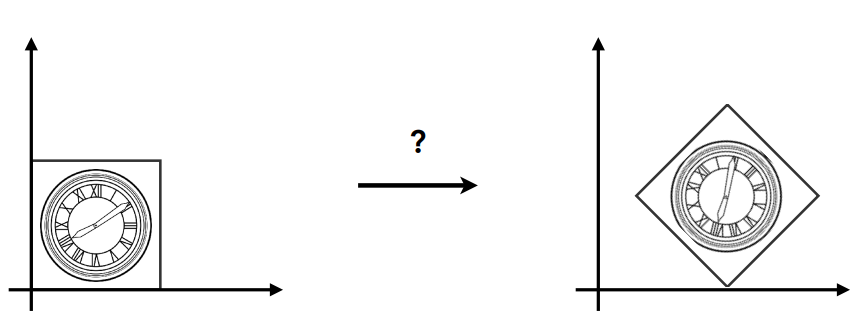
image-20220811155307566

变换的方法：先平移后旋转 or 先旋转后平移

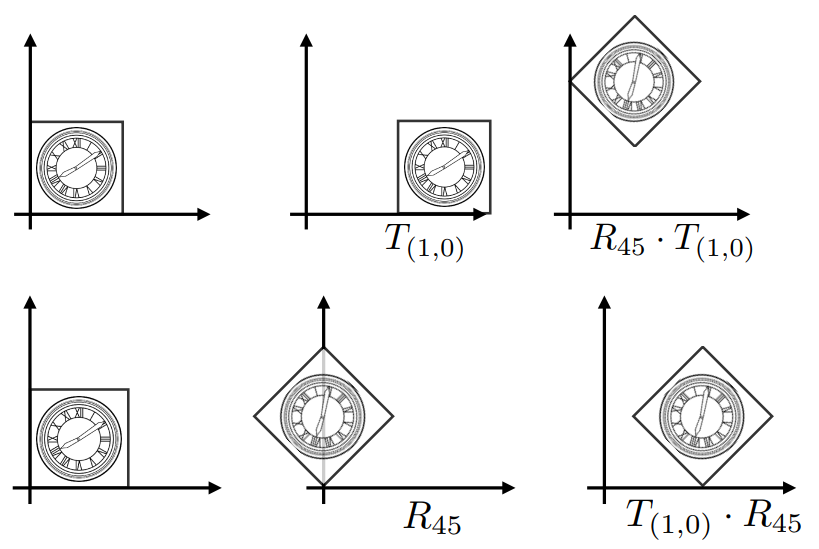
image-20220811155434542

矩阵表示：从右到左进行矩阵乘法，顺序为：缩放 => 旋转 => 平移

image-20220811155453930

3.3.2 多个变换

假设有一系列仿射变换\(A_1,A_2,A_3...\)

  1. 可以用矩阵乘法表示：

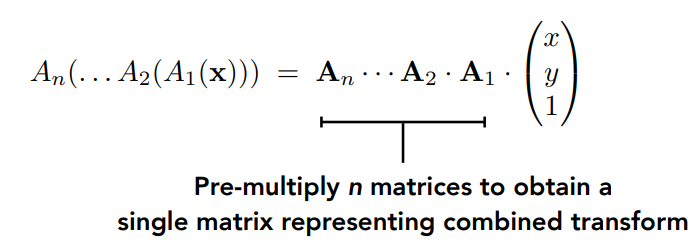
    image-20220811155912416

  2. 可以先计算\(A_n...A_2·A_1\)，再与列向量相乘

    1. 一个3*3的矩阵可以表示任意的变换

3.3.3 变换的分解

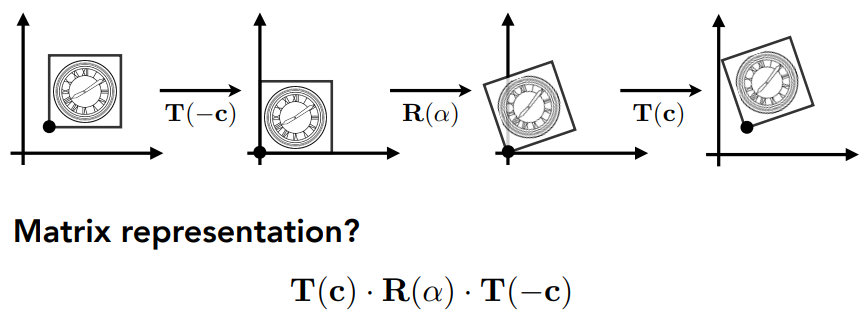
以C点为中心进行旋转\(\alpha\)度：\(T(\vec{c})·R(\alpha)·T(\vec{-c})\)

  1. 先将图形按照\(\vec{-c}\)的方向进行平移：\(T(\vec{-c})\)
  2. 然后绕原点旋转\(\alpha\)度：\(R(\alpha)\)
  3. 然后将图形按照\(\vec{c}\)的方向进行平移：\(T(\vec{c})\)

image-20220811160035313