GAMES101-04:变换2:三维变换
四、变换2:三维变换
4.0 有关旋转的补充
旋转矩阵的逆 == 旋转矩阵的转置 ==> 旋转矩阵为正交矩阵 $$ R_{}= ( \[\begin{matrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{matrix}\]) \
R_{-}= ( \[\begin{matrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{matrix}\]) =R_{}^T \
R_{-}=R_^{-1} $$
正交矩阵:\(R^T=R^{-1}\)
4.1 3D Transformations
4.4.1 齐次坐标
- 3维点:\((x,y,z,1)^T\)
- 3维点的补充形式:\((x,y,z,w)^T\)与\((\frac{x}{w},\frac{y}{w},\frac{z}{w},1)^T\)等价
- 3维向量:\((x,y,z,0)^T\)
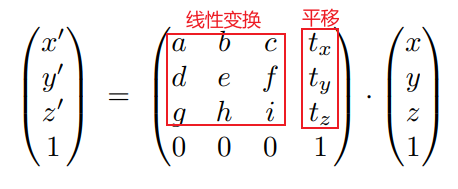
4.4.2 仿射变换
Affine Transform:
- 变换的顺序:先线性变换,后加平移量
4.4.2.1 缩放
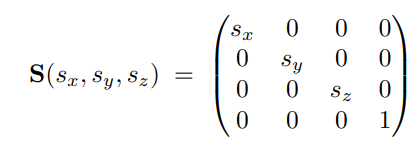
4.4.2.2 平移
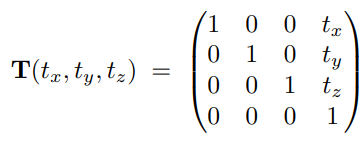
4.4.2.3 旋转
4.4.2.3.1 绕坐标轴旋转
绕X轴:X不变,YZ旋转
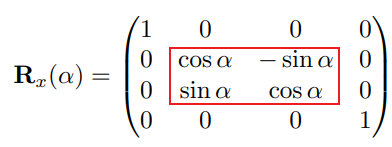
绕Y轴:Y不变,ZX旋转
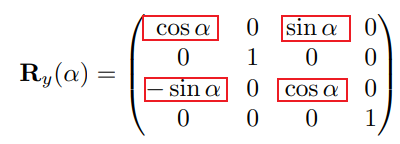
绕Z轴:Z不变,XY旋转

4.4.2.3.2 绕任意过原点的轴旋转
有两种形式:欧拉角、四元数
- 四元数:多应用于旋转的插值操作
绕任意轴旋转:分解为欧拉角
- 将任意轴方向的旋转,分解为绕X、Y、Z轴的旋转:\(R_{x,y,z}(\alpha,\beta,\gamma)\)
- \(\alpha,\beta,\gamma\)也被称为欧拉角
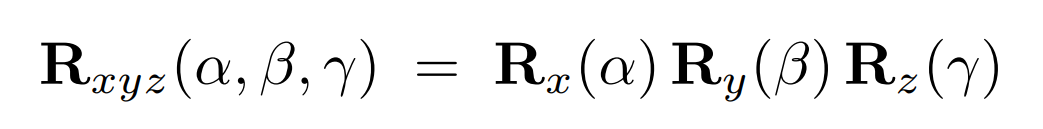
Rodrigues’ Rotation Formula 罗德里格旋转公式
- 向量v绕过原点的轴n旋转\(\alpha\)角
- 向量I为向量v方向的单位向量
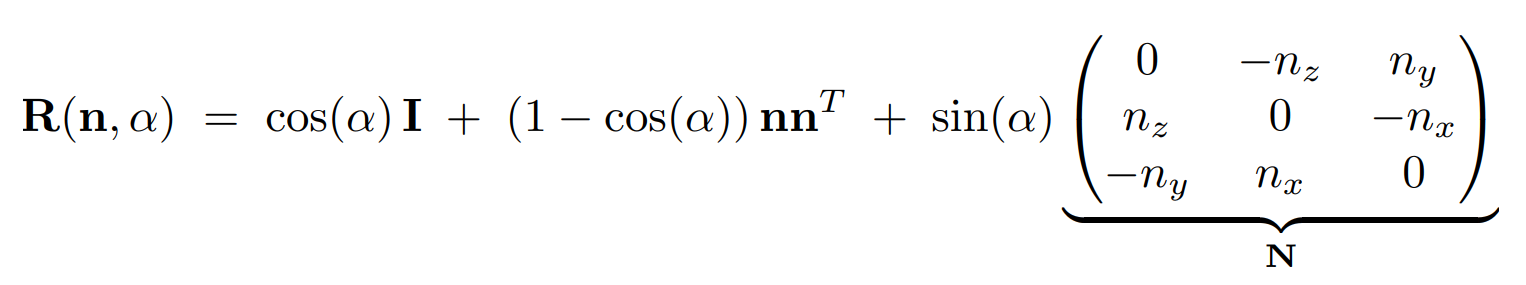
推导思路:
v与n垂直时,\(\vec{v'}=\cos\alpha*\vec{v}+\sin\alpha*(\vec{n}×\vec{I})\)
v与n不垂直时,将v分解为 垂直于n的向量v⊥ 和平行于n的向量v∥
- \(\vec{v_∥'}=\vec{v_∥}=|\vec{v}|*cos<\vec{v},\vec{n}>=\vec{v}·\vec{n}·\vec{n}\)
- \(\vec{v_⊥}=\vec{v}-\vec{v_∥}=\vec{v}-\vec{v}·\vec{n}·\vec{n}\)
- \(\vec{v_⊥'}=\cos\alpha*\vec{v_⊥}+\sin\alpha*(\vec{n}×\vec{v_⊥})\)
- 综上可得:\(\vec{v'}=\vec{v_∥'}+\vec{v_⊥'}=\cos\alpha*\vec{v}+(1-\cos\alpha)*\vec{v}·\vec{n}·\vec{n}+\sin\alpha*(\vec{n}×\vec{v})\)
矩阵形式:\(\vec{v'}=\cos\alpha*\vec{v}+(1-\cos\alpha)*\vec{v}·\vec{n}·\vec{n}+\sin\alpha*(\vec{n}×\vec{v})\)$
\(=[\cos\alpha*\vec{I}+(1-\cos\alpha)*\vec{n}·\vec{n}^T+\sin\alpha*(\vec{n}×\vec{I})]·\vec{v}\)
4.4.2.3.2 绕过任意点的任意轴旋转
绕过任意轴n旋转\(\alpha\)角
- 先将轴平移至过原点
- 然后旋转
- 最后平移回去
4.2 Model & View Transformation
4.2.1 什么是视图变换
- 与照相类比:MVP变换
| 照相 | 对应变换 |
|---|---|
| 找一个好的地方、人物排列 | 模型变换 model transformation |
| 找一个好的角度放置摄像机 | 视图变换 view transformation |
| 拍照,三维空间投影到二维平面 | 投影变换 projection transformation |
4.2.2 定义Camera
- 位置Position:\(\vec{e}\)
- 往哪看Look-at/gaze direction:\(\vec{g}\)
- 向上方向Up direction:\(\vec{t}\)
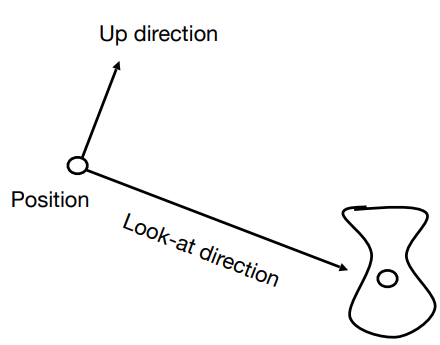
4.2.3 关键点:相机与物体的相对位置决定看到的图像
只要摄像机与物体的相对位置一样,所看到的图形就是一样的
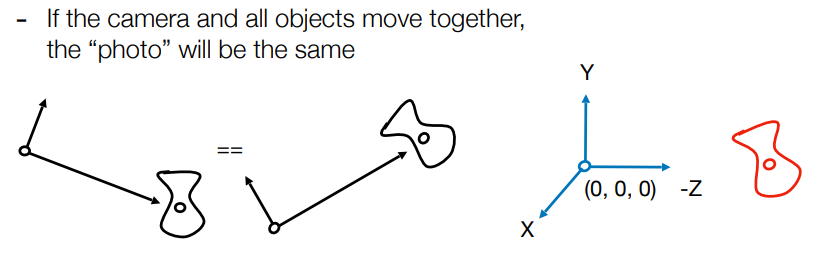
将摄像机永远放在一个标准的位置
- Position:原点
- Up direction:Y轴
- Look-at direction:-Z轴
当相机变换时,将物体随着相机变换
4.2.4 将相机移动到标准位置
方法
- 将\(\vec{e}\)平移到原点
- 旋转 \(\vec{g}\) 到-Z的方向
- 旋转 \(\vec{t}\) 到Y的方向
- 旋转 \(\vec{g}×\vec{t}\) 到X方向
矩阵表示:设\(M_{view}=R_{view}T_{view}\)
将\(\vec{e}\)平移到原点
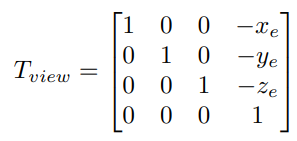
旋转 \(\vec{g}\) 到-Z、 \(\vec{t}\) 到Y、\(\vec{g}×\vec{t}\) 到X:考虑逆矩阵

4.2.5 总结
- 将物体与相机一起旋转:Model Transformation ==> \(M_{model}\)
- 将相机变换到标准位置:View Transformation ==> \(M_{view}\)
- Position:原点
- Up direction:Y轴
- Look-at direction:-Z轴
4.3 Projection Transformation
- 正交投影 Orthographic Projection:不存在近大远小
- 透视投影 Perspective Projection:存在近大远小,平行线不再平行
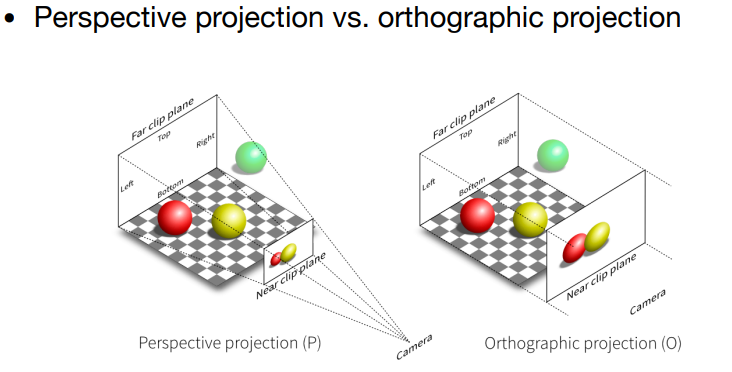
4.3.1 正交投影
Orthographic Projection:
- 思想:直接扔掉物体的Z坐标,然后将其移动到[-1,1]的标准范围内
实际做法:将一个立方体\([l, r]×[b, t]×[f, n]\)映射到标准立方体\([-1, 1]^3\)上
- 首先,通过平移操作,将立方体的中心移到原点
- 然后,通过缩放操作,将立方体缩放为标准立方体
- 立方体的定义:X轴\([l,r]\);Y轴\([b,t]\);Z轴\([f,n]\)
- 变换之后,物体一定会有拉伸
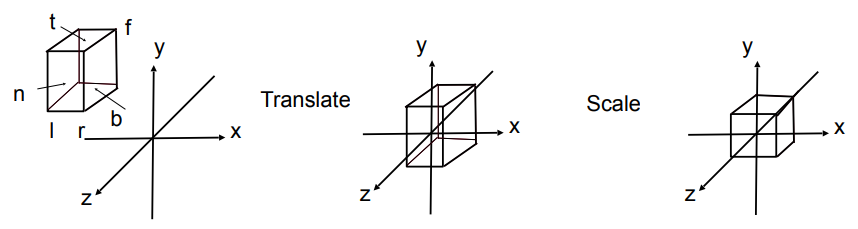
变换矩阵:先平移到原点,再将\(x,y,z\)缩放到\(2\)
$$ M_{ortho}= (
\[\begin{matrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix}\])
(
\[\begin{matrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \\ \end{matrix}\])
= (
\[\begin{matrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\ 0 & 0 & 0 & 1 \\ \end{matrix}\]) $$
4.3.2 透视投影
Perspective Projection
- 基础知识:\((x,y,z,1)\)与\((kx,ky,kz,k)\)表示同一个点,因此\((xz,yz,z^2,z)\)表示的也是这个点
- 思想:将透视投影转化为正交投影\(M_{persp->ortho}\),然后再进行正交投影变换\(M_{ortho}\)
4.3.2.1 如何进行透视投影
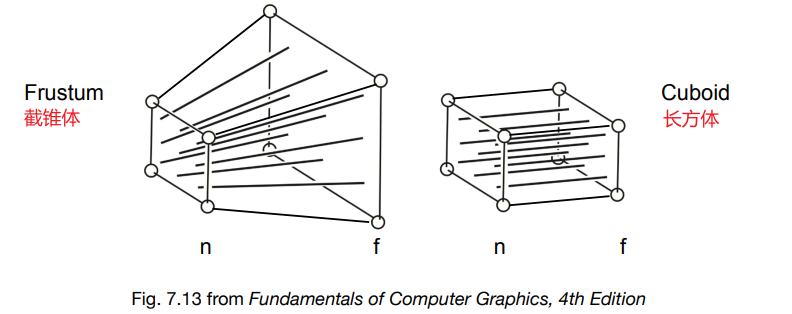
- 首先,定义从相机点向外的两个平面n、f,f平面要比n平面大
- 此时就相当于f平面上的点全部投影到n平面上
- 透视投影的做法
- 先将Frustum挤成Cuboid(\(n \rightarrow n,f \rightarrow
f'\)),满足如下三个定义:\(M_{persp->ortho}\)
- 近平面\(n\)永远不变
- 远平面\(f\)的Z值永远不变
- 远平面\(f\)的中心点\((0,0,f)\)永远不变
- 再进行一次正交投影:\(M_{ortho}\)
- 先将Frustum挤成Cuboid(\(n \rightarrow n,f \rightarrow
f'\)),满足如下三个定义:\(M_{persp->ortho}\)
4.3.2.2 计算矩阵\(M_{persp->ortho}\)
思路:找到变换后的点\((x',y',z')\)与原来的点\((x,y,z)\)的对应关系
从YZ平面上看,挤压前后存在相似三角形,从而可得到\(y'=\frac{n}{z}*y\)
- 同理,\(x'=\frac{n}{z}*x\)
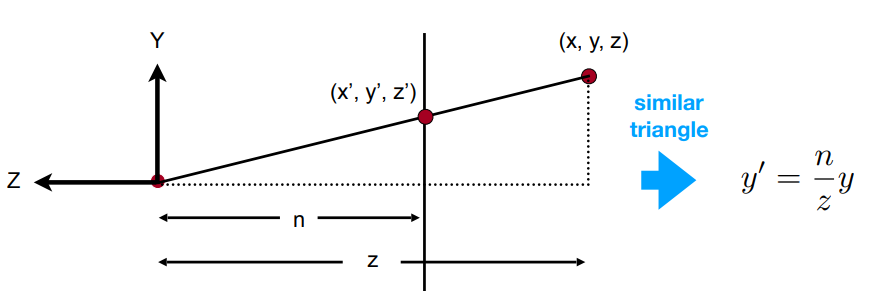
齐次坐标表示
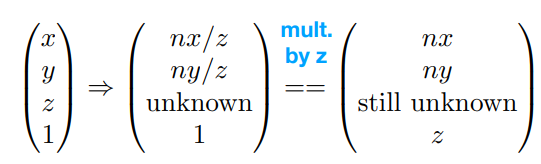
矩阵表示
由3得 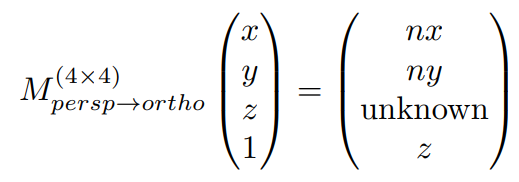
因此 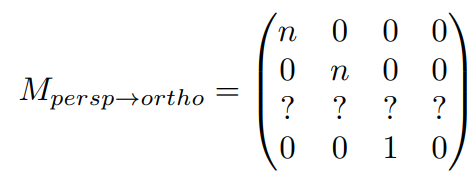
对于矩阵的第三行(对于Z值),有以下性质
在近平面上的点,坐标不变 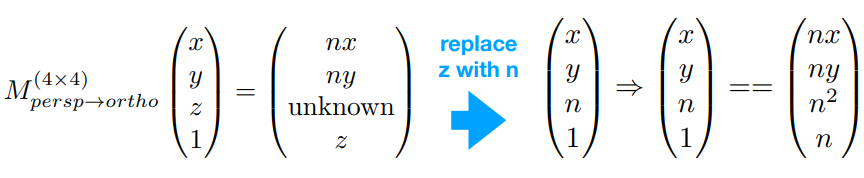
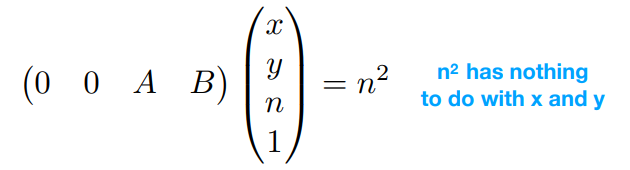
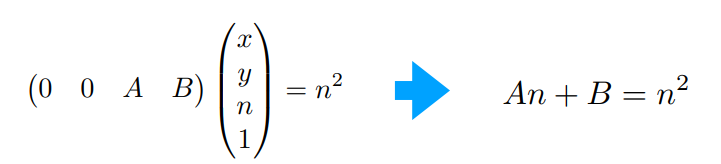
在远平面上的中心点\((0,0,f)\),坐标不变 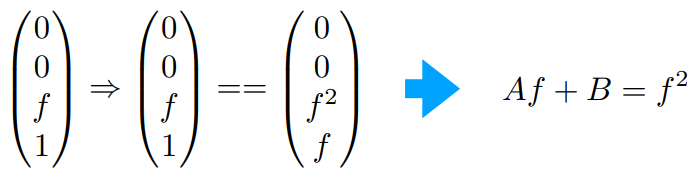
根据两个等式,可以解出\(A,B\) 
综上 \[ M_{persp \rightarrow ortho}= \left( \begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \\ \end{matrix} \right) \]
最后,再进行正交投影:\(M_{persp}=M_{ortho}M_{persp->ortho}\)
)
( \[\begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \\ \end{matrix}\])
=
( \[\begin{matrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0 \\ 0 & 0 & \frac{n+f}{n-f} & -\frac{2nf}{n-f} \\ 0 & 0 & 1 & 0 \\ \end{matrix}\]) $$
4.3.3.3 对于不在近/远平面上的点
$$ ( \[\begin{matrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \\ \end{matrix}\])
( \[\begin{matrix} x \\ y \\ z \\ 1 \\ \end{matrix}\])
( \[\begin{matrix} nx \\ ny \\ (n+f)z-nf \\ z \\ \end{matrix}\])
==> ( \[\begin{matrix} \frac{n}{z}x \\ \frac{n}{z}y \\ (n+f)-\frac{nf}{z} \\ 1 \\ \end{matrix}\]) $$
- 近平面上的点\((z=n)\)
- \(z'=(n+f)-\frac{nf}{n}=n\)
- \(z'=z\)
- 远平面上的点\((z=f)\)
- \(z'=(n+f)-\frac{nf}{f}=f\)
- \(z'=z\)
- 不在近/远平面上的点\((f<z<n)\)
- \(z'=(n+f)-\frac{nf}{z}\)
- 设\(n=1,f=-1,z=0.5\),则\(z'=2\)
- 设\(n=1,f=-1,z=-0.5\),则\(z'=-2\)
- 可得:若\(z<0\),则\(z'\)更靠近远平面\(f\);若\(z>0\),则\(z'\)更靠近近平面\(n\)
- \(z'=(n+f)-\frac{nf}{z}\)
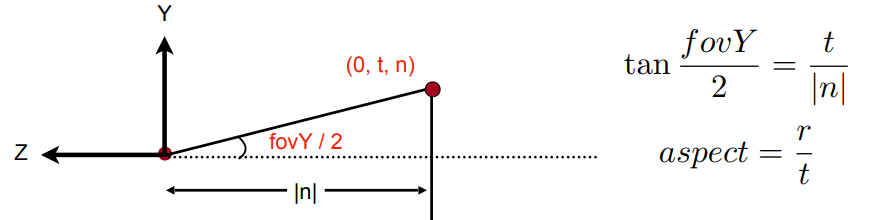
4.3.3.4 定义视锥
定义一个视锥,需要
- 宽高比:Aspect ratio
- 垂直的可视角度:Vertical Field of View
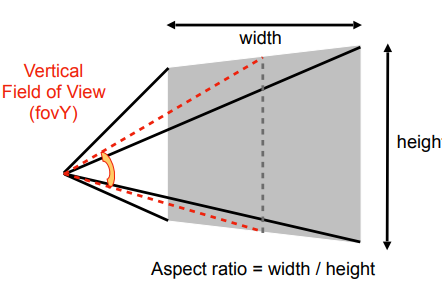
Aspect ratio 纵横比:\(\frac{width}{height}\)
field-of-view(fovY)视野:从摄像机所在位置出发,连接屏幕宽的两个中点,两条线所夹的角度
从fovY和Aspect推出l, r, b, t