六、光栅化2：反走样&深度缓冲

Antialiasing and Z-Buffering

  1. Artifacts：瑕疵，指一切看上去不太对的地方

  2. 采样可能产生的瑕疵：

    1. 锯齿

      image-20230226185128331

    2. 摩尔纹：将左图的奇数行和奇数列删除，会产生右面的效果

      image-20230226185149464

  3. 车轮效应：车轮高速逆时针旋转时，看上去好像是在顺时针旋转

现象 原因
锯齿 Jaggies 在空间上的采样率不足
摩尔纹 Moire 对一个图像降低采样率
车轮效应 Wagon wheel effect 在时间上的采样率不足

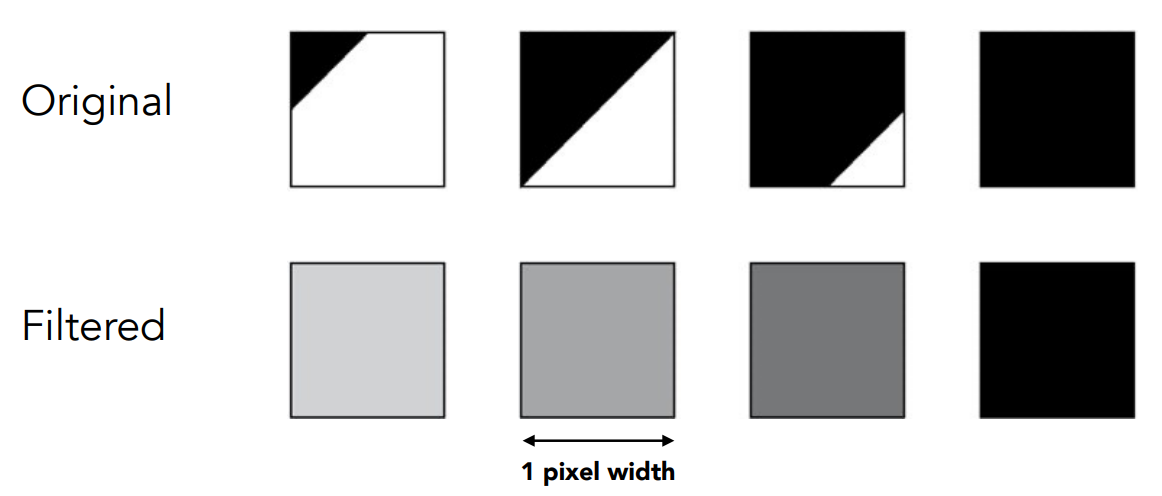
6.1 反走样方法：在采样之前进行过滤/模糊处理

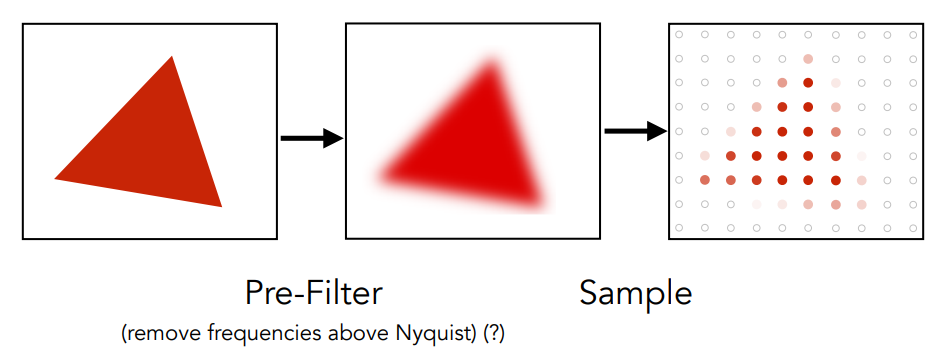
image-20230226185816066

6.1.1 先滤波，后采样：Aliasing

原始图片 点采样 模糊处理抗锯齿
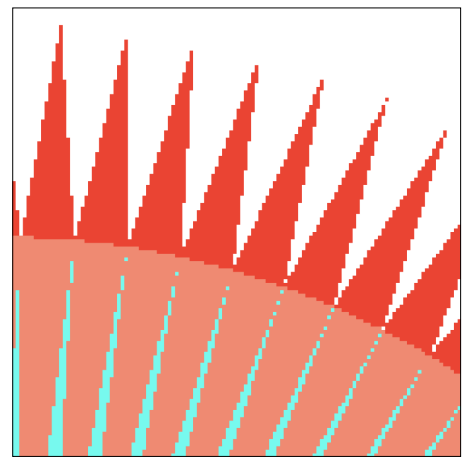
image-20230226185933649 image-20230226185944079 image-20230226185951932

6.1.2 先采样，后滤波：Blurred Aliasing

image-20230226190155171

6.2 频率域

6.2.1 空间域 与 频率域的转换：傅里叶变换

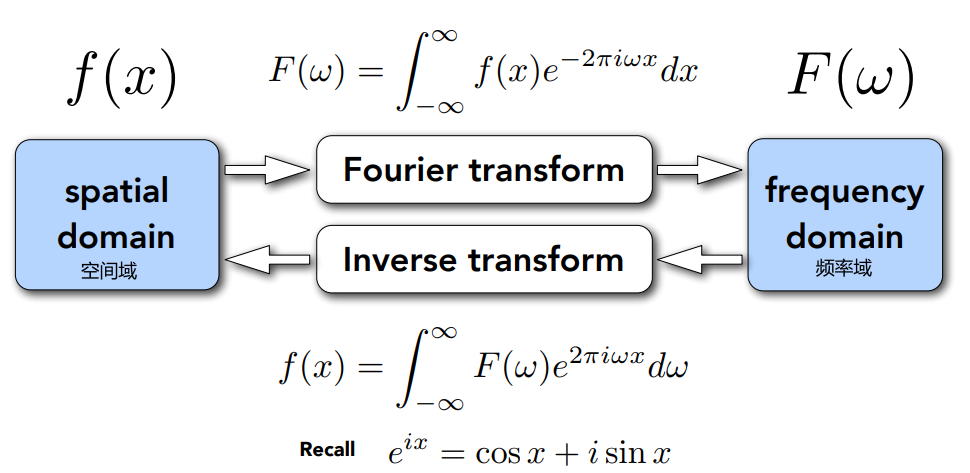
image-20230226191158596

  1. 任何一个函数，均可以展开为多个三角函数的和
  2. 傅里叶变换，实际上就是将函数在不同频率域上展开

6.2.2 函数的频率越高，需要的采样频率越高

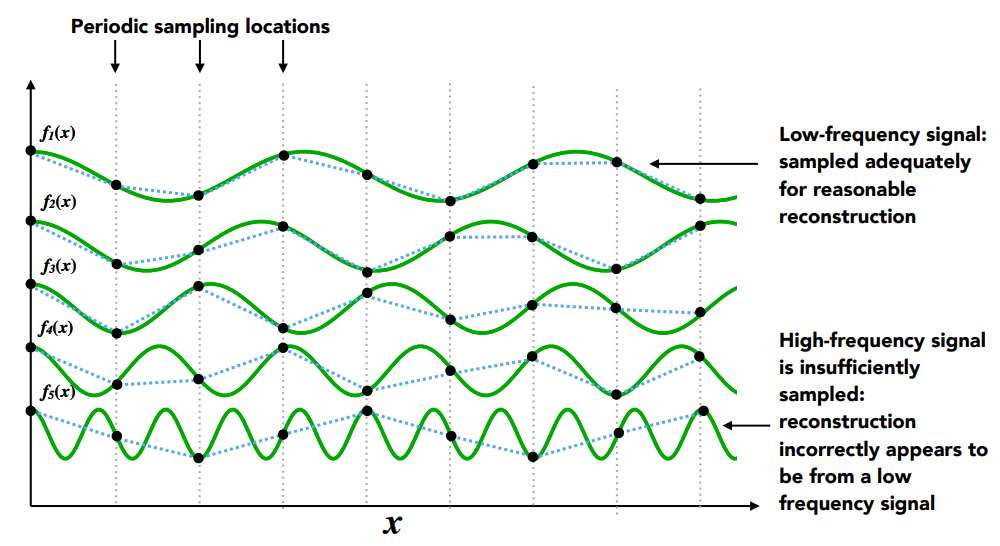
image-20230226191506715

6.2.3 从频率角度理解走样

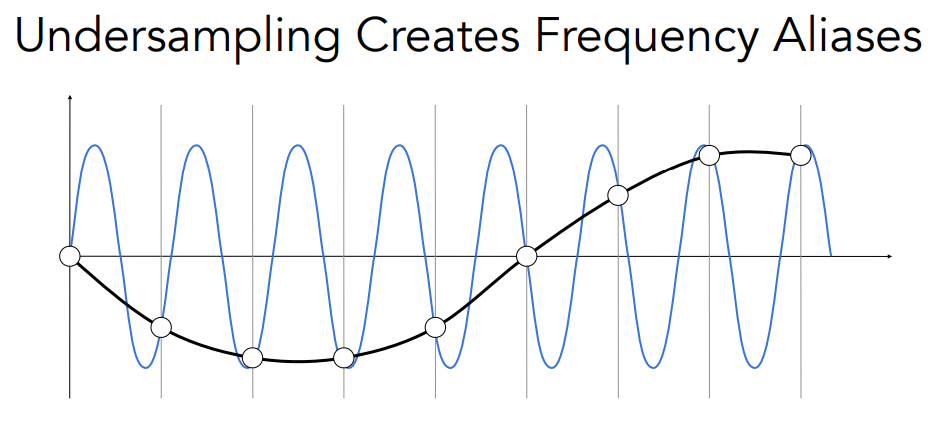
image-20230226191902811

  1. 在采样频率一定时，采样两个频率不同的函数，我们无法区分这两个函数，因此会产生锯齿

6.3 滤波：删除一些频率的内容

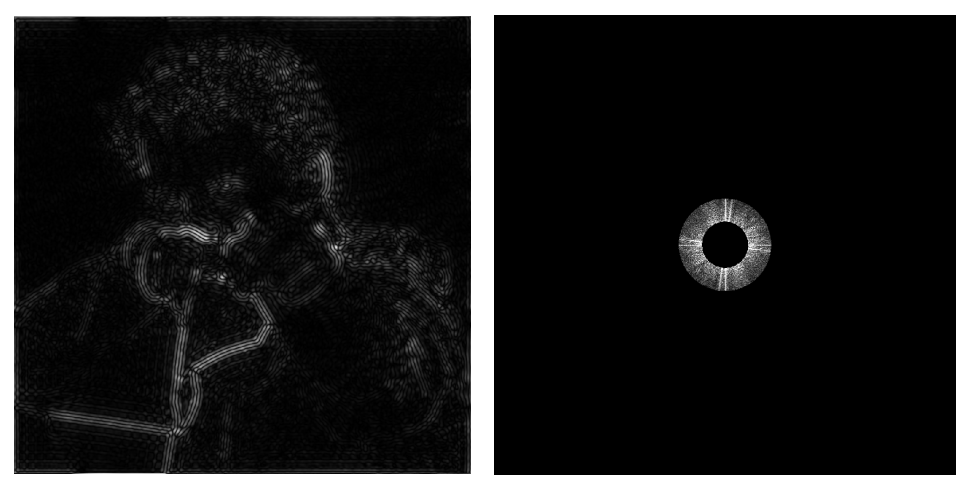
6.3.1 通过傅里叶变换，将图像变为频率图

image-20230226192200644

  1. 中心是低频区，四周是高频区
  2. 亮度表示当前频率包含的信息数量
  3. 上图的信息主要集中在低频区
  4. 出现两条线的原因
    1. 一般情况下，傅里叶变换会将图像视为周期函数
    2. 对于图片来说，相当于在图像的右边再复制一份图像
    3. 通常情况下，图片的左右边界不会相同，因此在边界处会有剧烈的变换
    4. 分析图像内部的内容时，一般忽略这两条线

6.3.2 高通滤波

高通滤波 ==> 只保留图像的高频部分 ==> 图像内容的边界

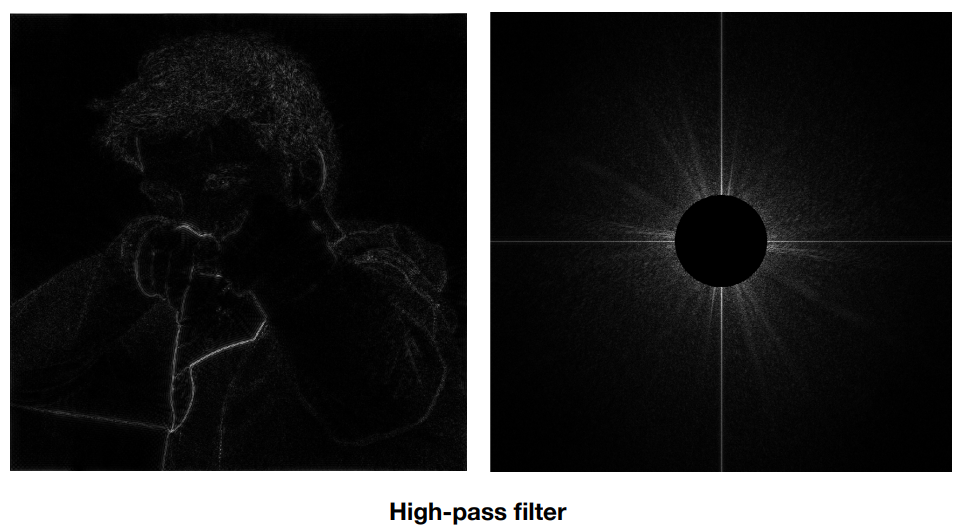
image-20230226192757970

6.3.3 低通滤波

低通滤波 ==> 只保留图像的低频部分 ==> 对图像的模糊处理

image-20230226192911384

6.3.4 过滤高频和低频部分

image-20230226193200309

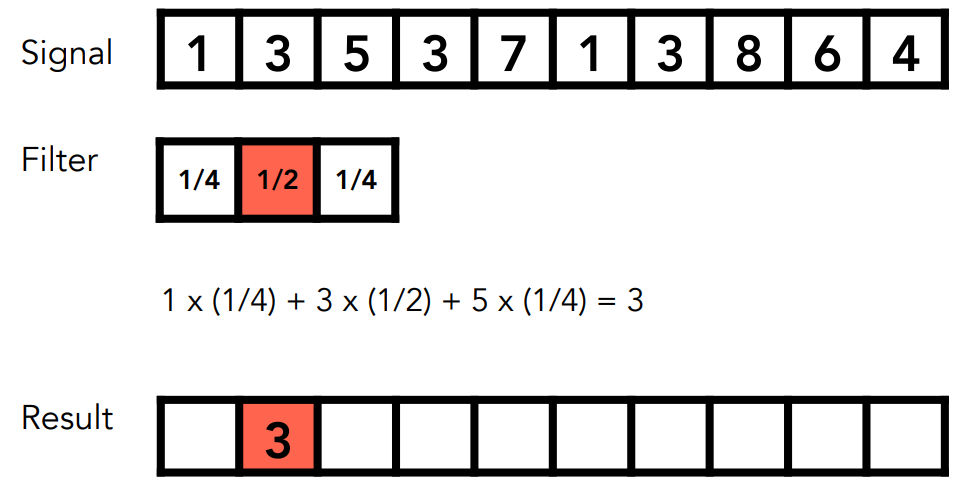
6.4 滤波 = 平均 = 卷积

Filter = Averaging = Convolution

  1. 滤波器覆盖信号的某些部分时，将对应位做点乘：卷积操作
  2. 实际上也是一个平均操作

image-20230226193458236

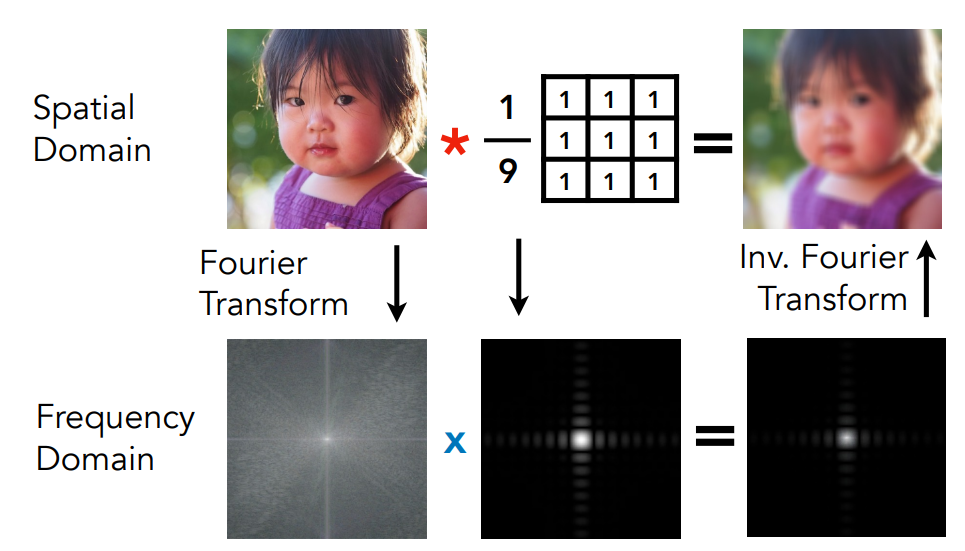
6.4.1 卷积定理：时域的卷积 <=> 频域的乘积

卷积定理：在时域上的卷积，等价于在频域上的乘积，即以下两个操作等价

  1. 在时域上，通过卷积进行滤波
  2. 先通过傅里叶变换，将函数与滤波器转换到频域上；然后把两者相乘；最后再进行逆傅里叶变换，变换到时域上

image-20230226194122537

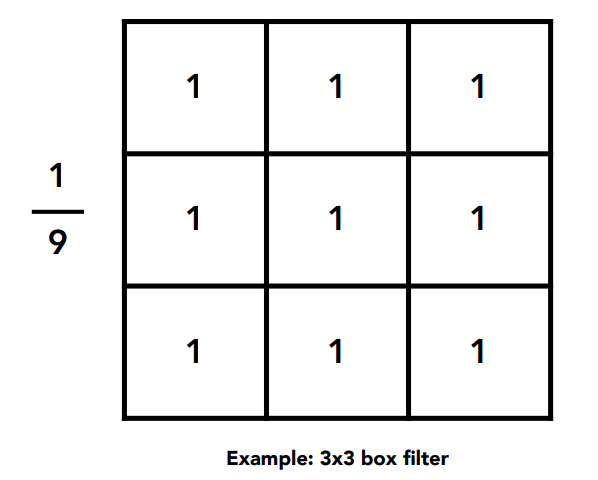
6.4.2 滤波器的时域与频域的关系

时域上变大了，频域上反而变低了：Box越大，得出的结果越模糊

image-20230226194605360

image-20230226194506188

image-20230226194514473

6.5 频率角度理解采样

6.5.1 采样 = 重复原始信号的频谱

采样频率越快，频谱复制越稀疏

采样频率越满，频谱复制越密集

时域上采样 <=> 两个函数相乘 频域上的卷积 <=> 重复原始信号的频谱
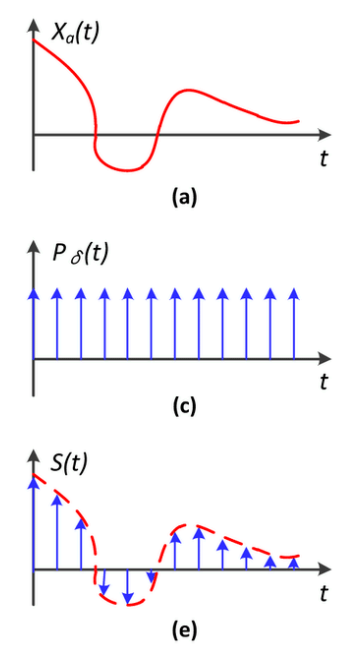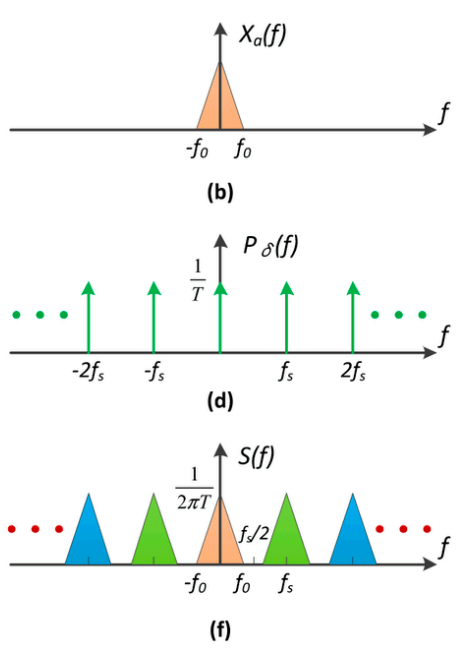image-20230226194857621 image-20230226194911883

6.5.2 走样 = 频谱的内容出现重叠

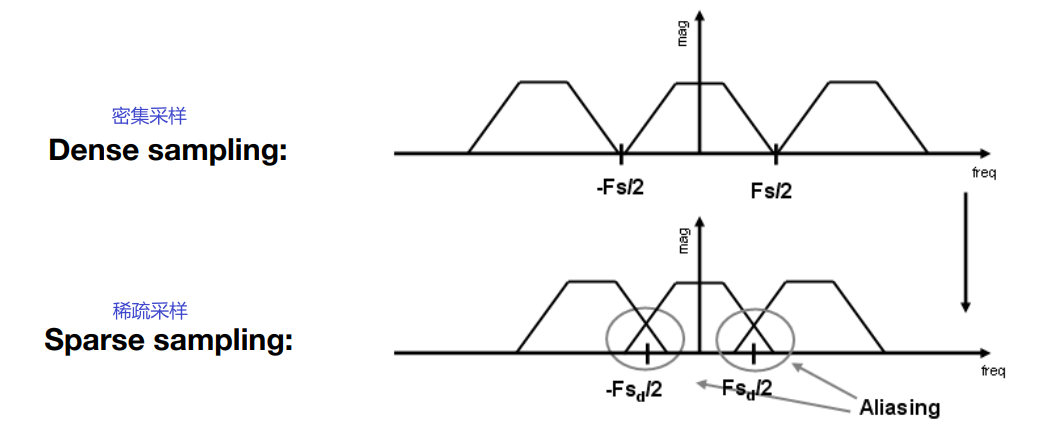
image-20230226195426029

6.5.3 反走样 = 先删除高频信息，在采样

  1. 先模糊，后采样：先删除一个信号的高频信息，然后在进行采样

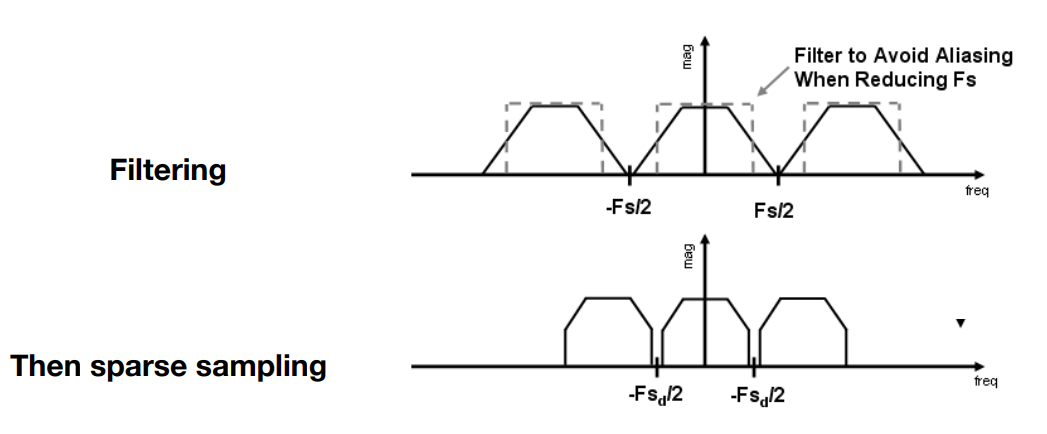
image-20230226195656888

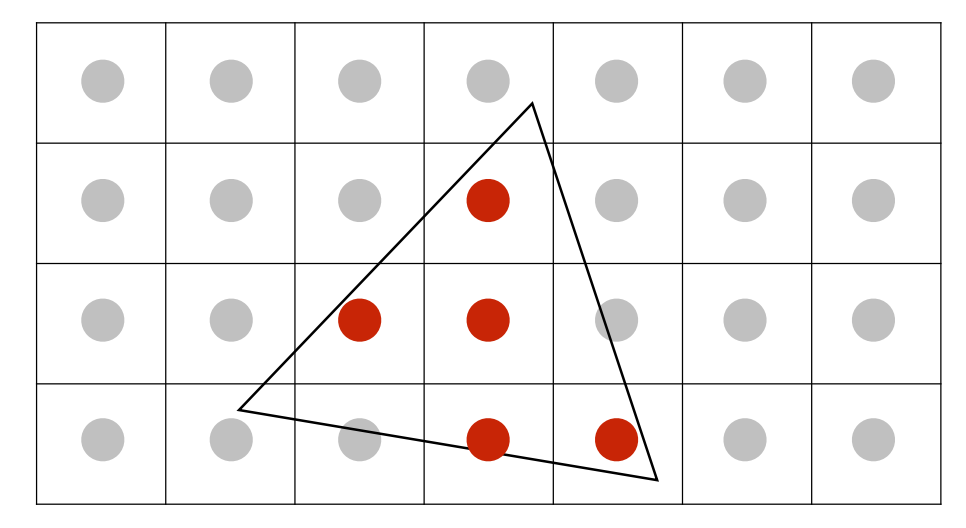
6.6 反走样的实际做法

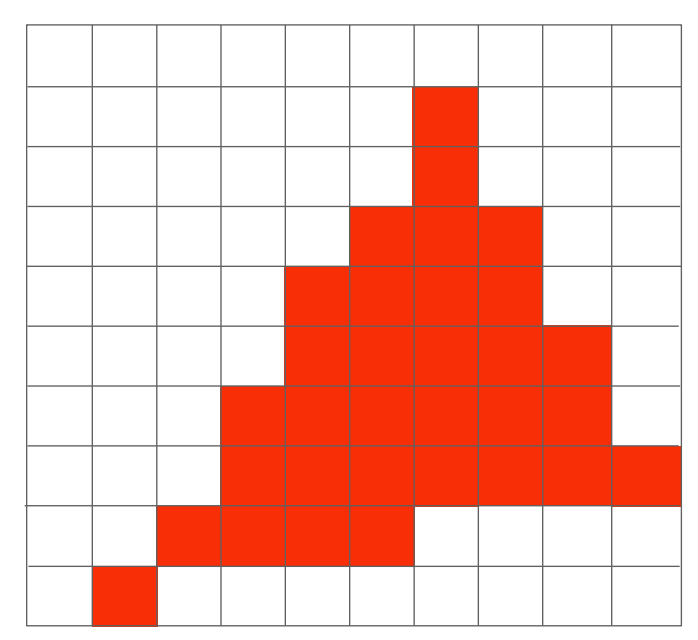
  1. 对每个像素，根据三角形覆盖的面积，做平均值
  2. 然后再进行采样

image-20230226200044458

6.6.1 MSAA：Multisample Antialiasing

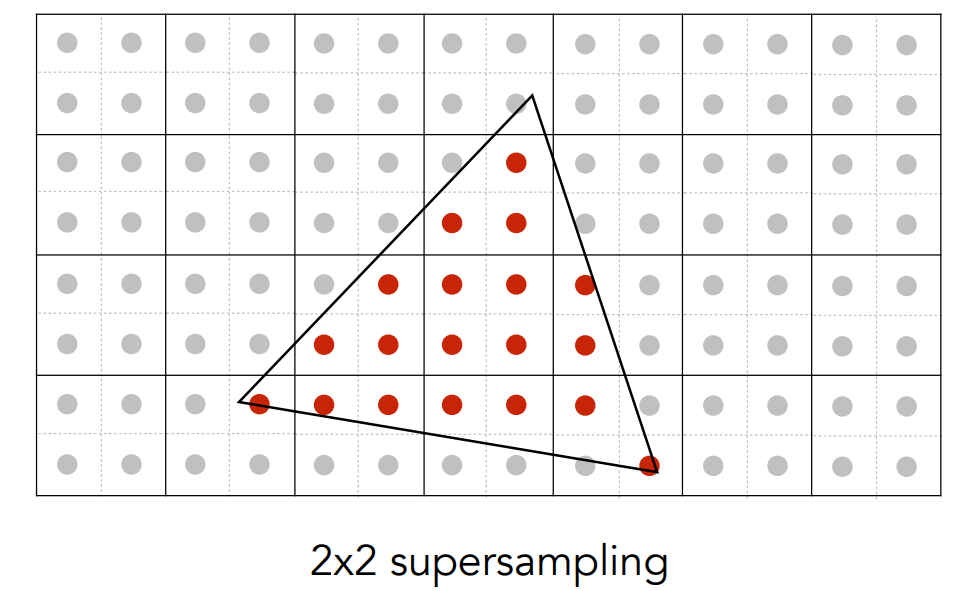
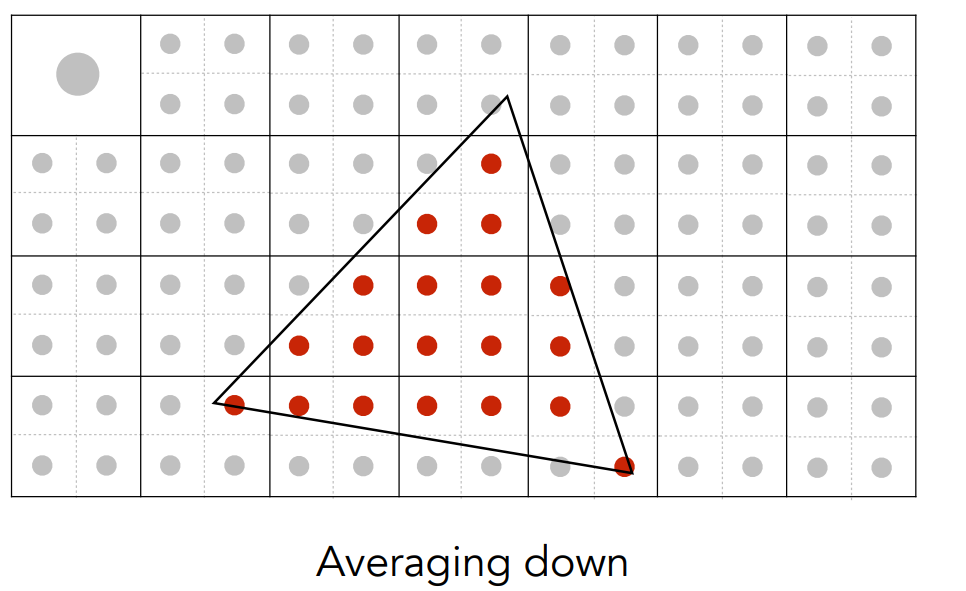
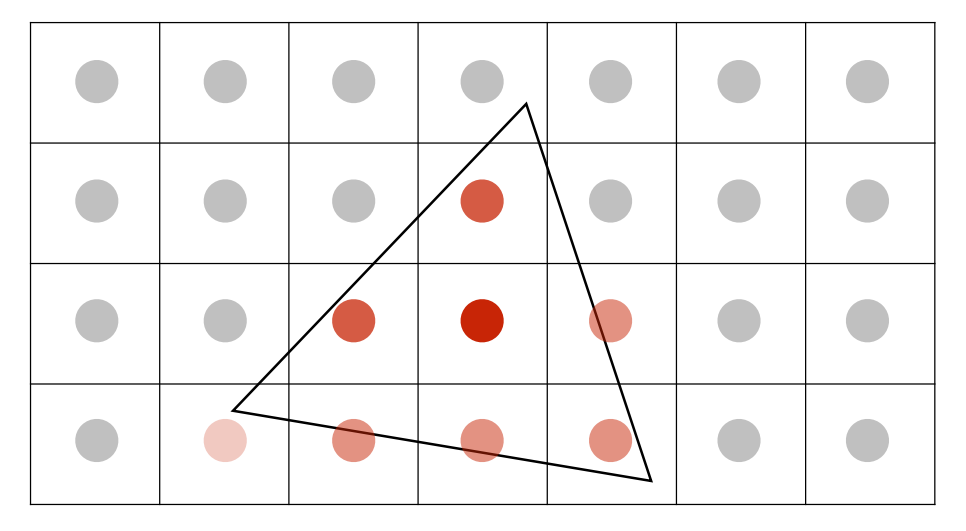
  1. 超采样 SuperSampling：将每个像素划分为多个小的采样点，然后该像素的颜色为多个采样点的平均
  2. MSAA近似的是抗锯齿的第一步操作，即模糊处理
  3. MSAA无法提高屏幕的分辨率，只是通过多个采样点得到近似的三角形覆盖
  4. MSAA是通过增大计算量，得到抗锯齿效果
  5. 在实际使用中，会将采样点按特殊的方法排列，有些采样点还会被多个像素复用

image-20230226201008321

image-20230226201027928

image-20230226201036128

image-20230226201053512

image-20230226201100860

6.6.2 FXAA：Fast Approximate Antialiasing

  1. 快速近似抗锯齿
  2. 通过图像的后期处理，先将有锯齿的图像得出来，然后通过图像匹配找到边界，将这些像素换为边界上的颜色

6.6.3 TAA：Temporal Antialiasing

  1. 通过找上一帧的信息，进行抗锯齿操作
  2. 假设是静止画面，在相邻两帧同一个像素用不同的点感知是否在一个三角形内
  3. 复用上一帧感知到的值，相当于将MSAA的采样点分布在时间上，对于具体的某一帧没有额外操作

6.7 超分辨率/超采样

  1. 采样率不够，而分辨率较大时，会使用这种技术
  2. DLSS：Deep Learning Super Sampling，通过深度学习，猜测丢失的信息

6.8 深度缓冲：解决可见性

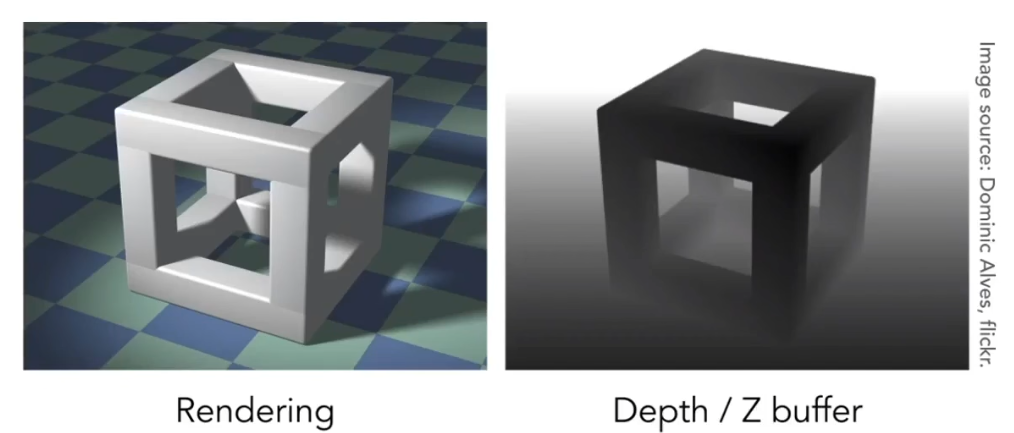
image-20230316201036427

  1. Z-Buffer：存储每一个像素，所看到的几何物体的最浅距离
    1. 设Z始终为整数，且Z越小离相机越近
  2. 具体算法：
    1. 初始化深度缓存为∞
    2. 对于每一个三角形T
      1. 对于T中的每一个采样点(x,y,z)：
      2. 如果Z < z-buffer[x,y]：更新frame-buffer、z-buffer
      3. 否则，跳过该采样点
  3. 复杂度
    1. 有n个三角形，则复杂度为O(n)
    2. 此处并没有排序，而是对每一个像素，维护了一个最小值
  4. 画出来的结果，与画三角形的顺序无关
  5. 深度缓存无法处理透明物体