七、着色1：Blinn-Phong反射模型

Shading：着色

  1. 对不同物体，定义不同材质，从而与光线产生不同作用

局部性：

  1. 只考虑自己的属性，不考虑与其他物体的存在
  2. 因此，没有阴影
image-20230316203039767

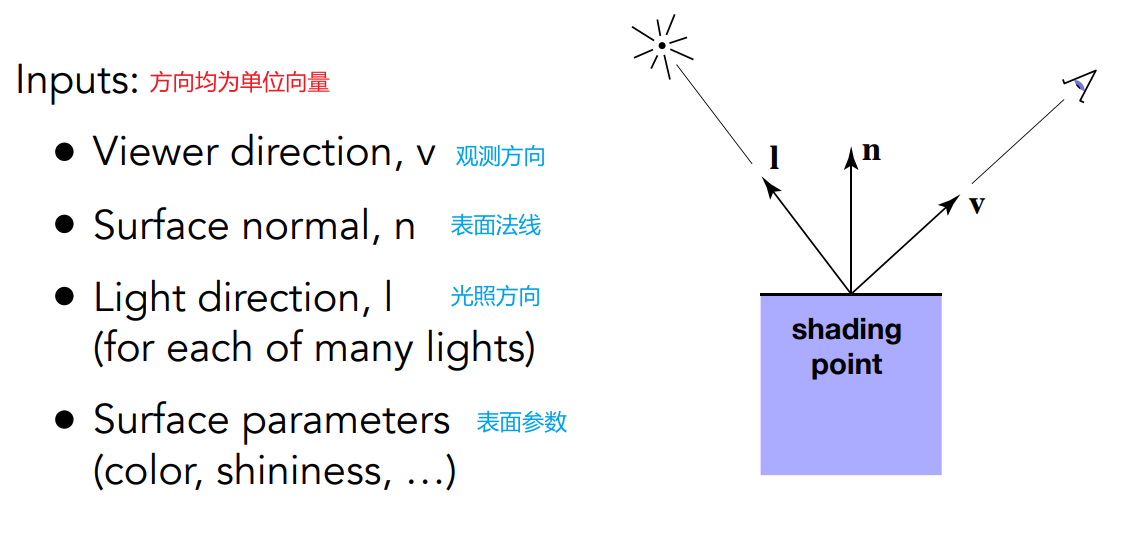
7.1 反射模型的输入

image-20230316203536809

7.2 光照的能量传递关系

  1. 余弦定理：单位面积接收到的光的能量占比为cos θ，θ为光照方向与平面法线的夹角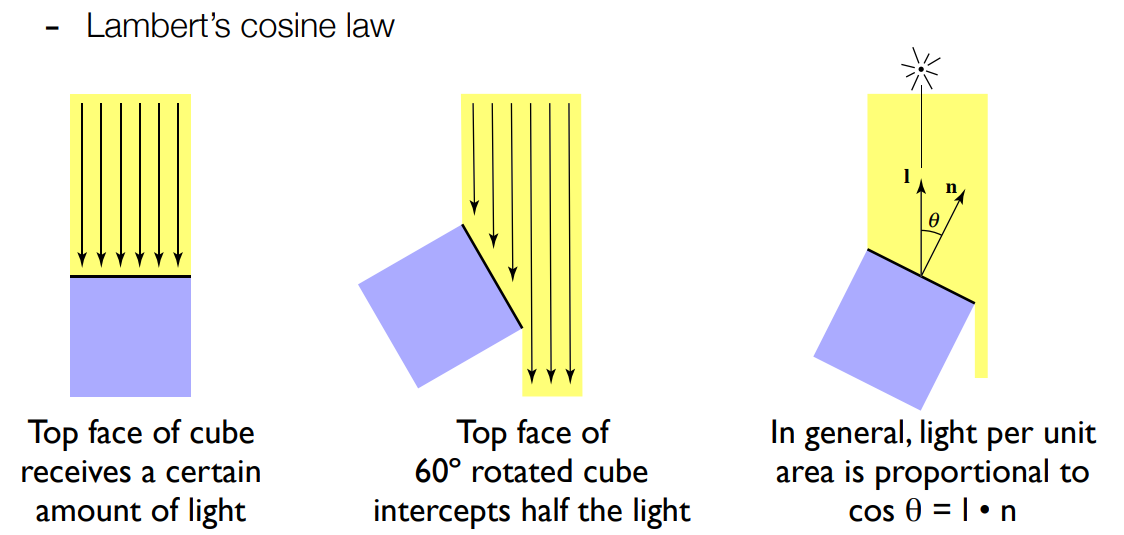

    image-20230316204159302

  2. 设光源的能量为I，光源与表面的距离为r，则到达表面的能量为\(\frac{I}{r^2}\)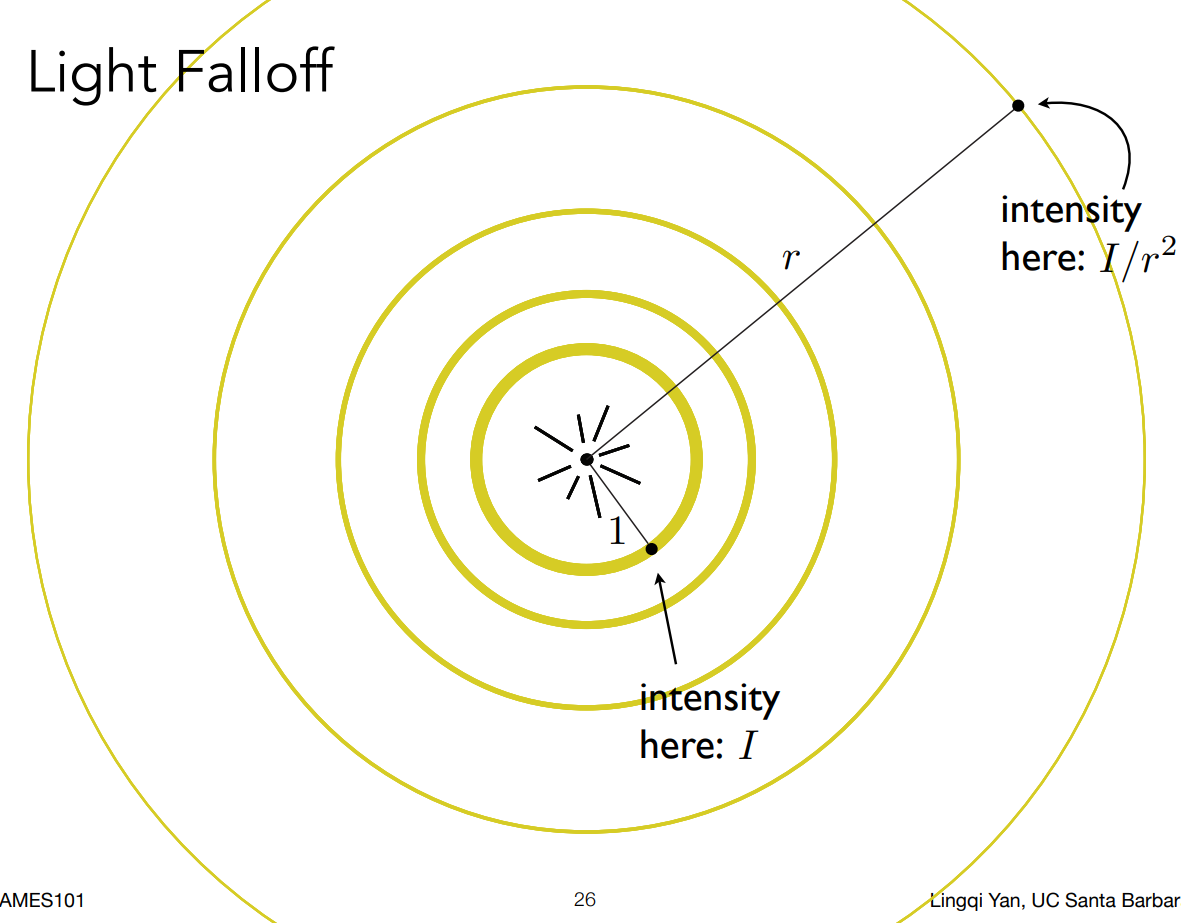

    image-20230316204518794

7.3 漫反射 Diffuse Reflection

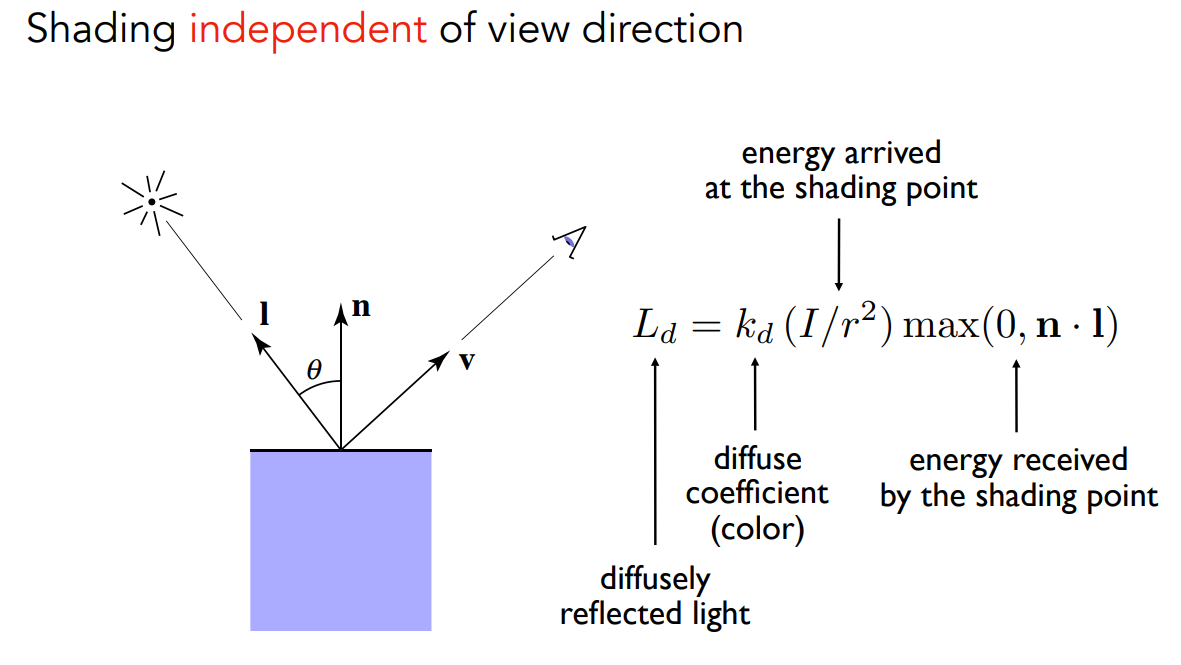
\[ L_d=k_d\frac{I}{r^2}max(0,\vec{n}·\vec{l}) \]

  1. \(L_d\)：漫反射光照
  2. \(k_d\)：漫反射系数，通常为物体的颜色
  3. \(I/r^2\)：到达该点的能量
  4. \(max(0,\vec{n}·\vec{l})\)：该点接收到的能量
  5. 由于漫反射到四面八方的能量均相同，因此没有\(\vec{v}\)的事情

image-20230316204556352

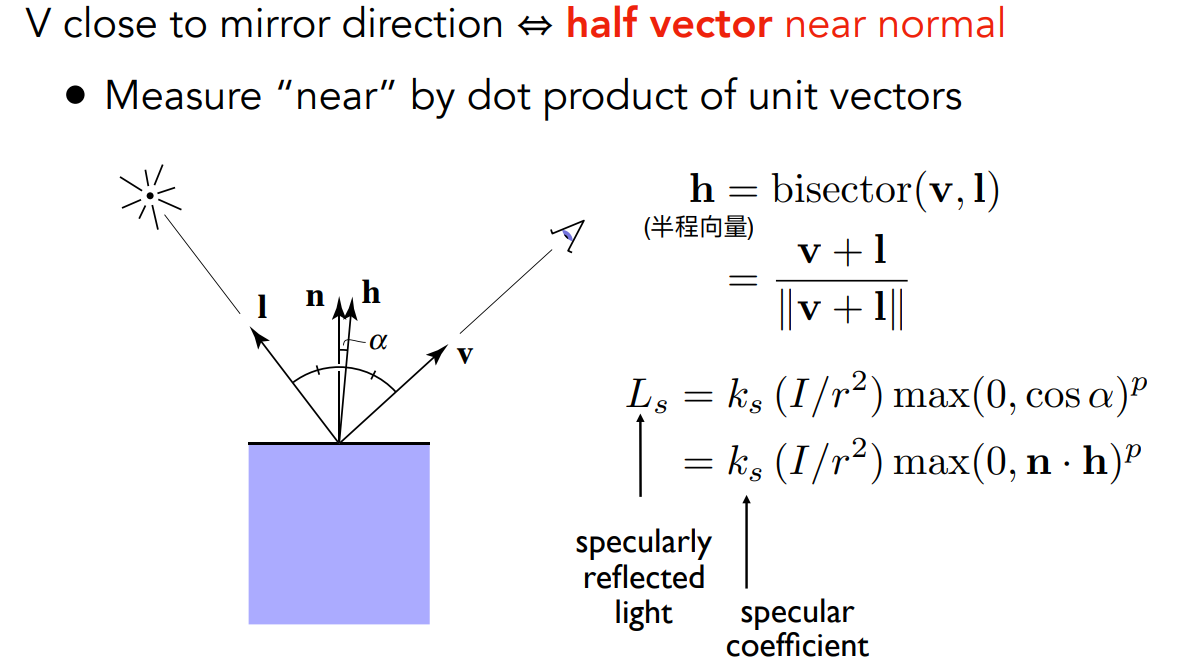
7.4 镜面反射&高光项 Specular Reflection

接近镜面反射时，会出现高光

\[ L_s=k_s\frac{I}{r^2}max(0,\vec{n}·\vec{h})^p \]

  1. \(L_s\)：镜面反射光照
  2. \(k_s\)：镜面反射系数，通常为白色
  3. \(I/r^2\)：到达该点的能量
  4. \(max(0,\vec{n}·\vec{l})\)：该点接收到的能量
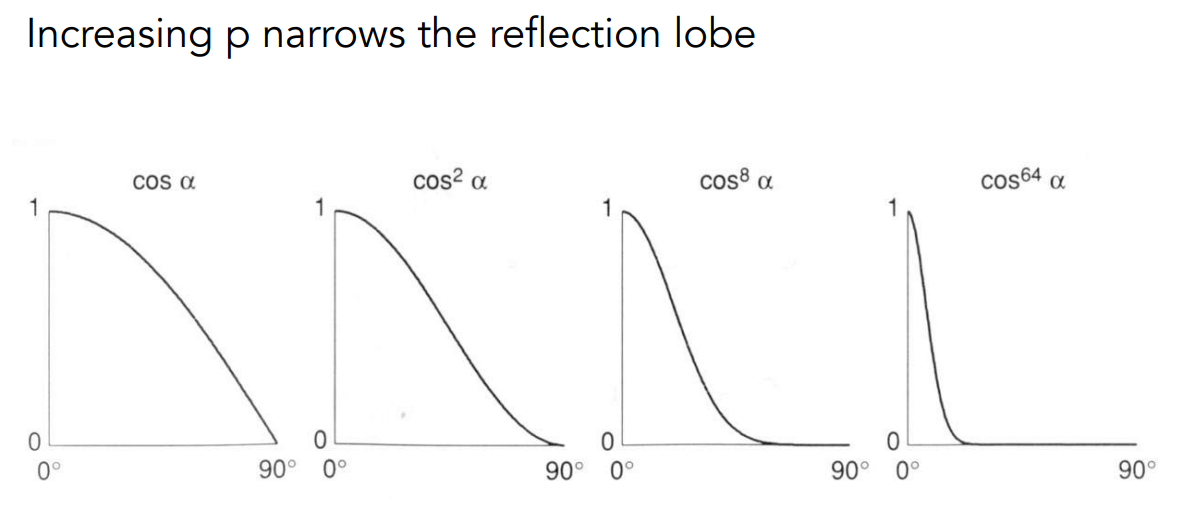
  5. \(p\)：为了让高光的区域足够小，需要将夹角余弦进行幂操作

image-20230316205631263

image-20230316220333380

7.5 环境光 Ambient Term

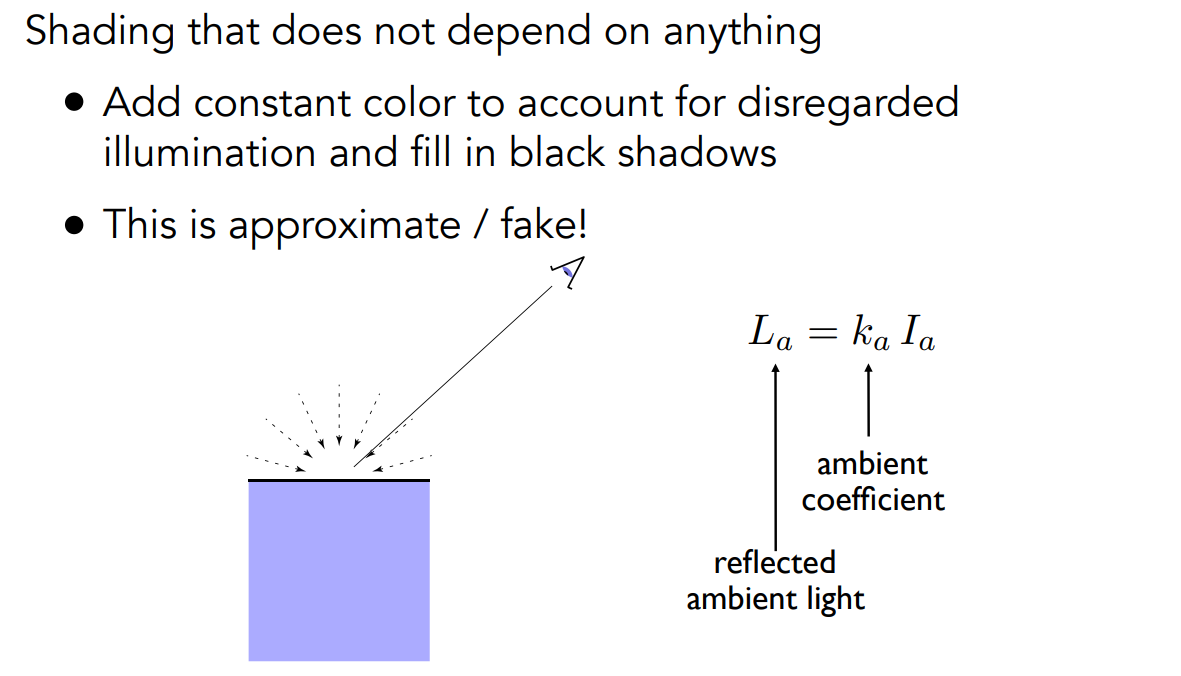
假设所有点接收到的环境光均相同

\[ L_a=k_aI_a \]

  1. \(L_a\)：环境光
  2. \(k_a\)：环境光系数，通常为物体颜色
  3. 环境光通常为一个常量，保证没有地方是黑的

image-20230316220425251

7.6 Blinn-Phong反射模型

\[ \begin{aligned} L &= L_a+L_d+L_s\\ &= k_aI_a+k_d\frac{I}{r^2}max(0,n·l)+k_s\frac{I}{r^2}max(0,n·h)^p \end{aligned} \]

image-20230316220636330