九、着色3：纹理的应用

9.1 重心坐标 Barycentric Coordinates

为什么需要插值

  1. 我们的很多操作是定义在顶点上的
  2. 我们需要在三角形内获得平滑的值

插值什么内容

  1. 纹理坐标、颜色、法线

怎么做插值

  1. 重心坐标

9.1.1 重心坐标是什么

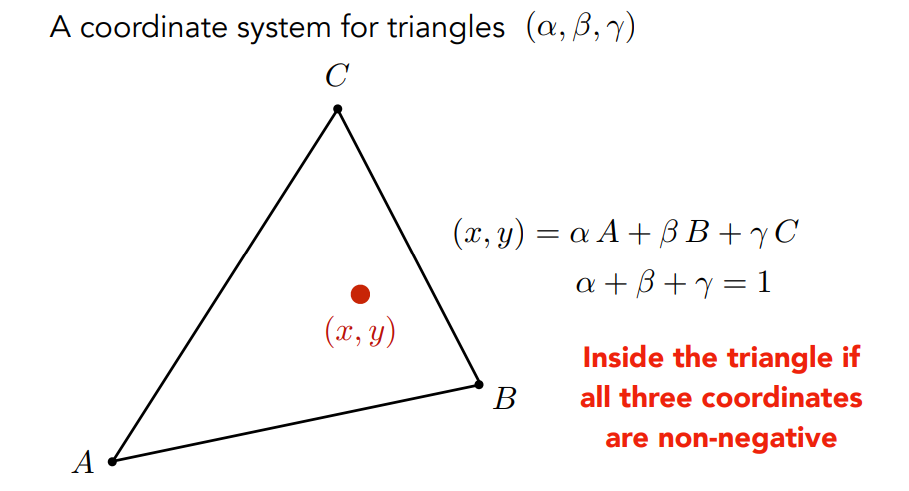
image-20230320181655673

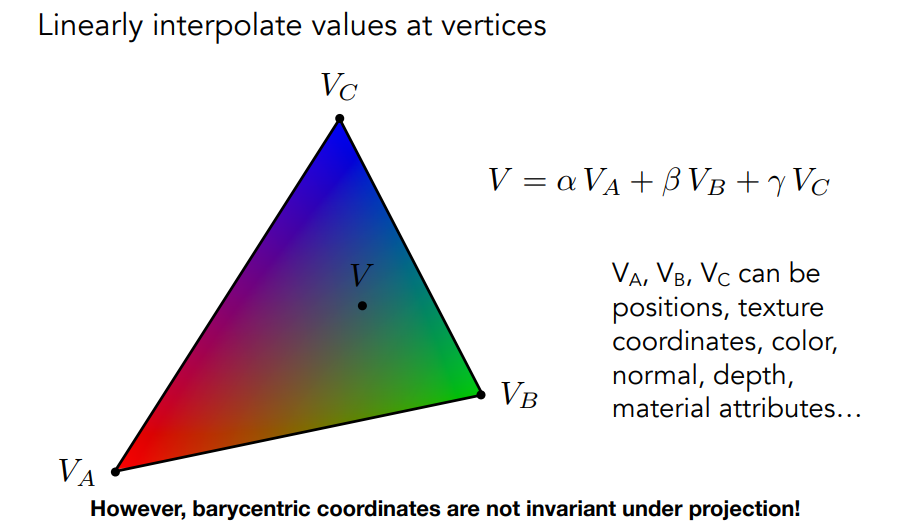
  1. 定义在三角形上：三角形所在平面的任意一个点的坐标，都可以用三个顶点坐标的线性组合表示，且\(\alpha+\beta+\gamma=1\)

    1. \((x,y)=\alpha A+ \beta B + \gamma C\)，可以得到一个坐标\((\alpha,\beta,\gamma)\)
    2. 如果在三角形内，则\(\alpha,\beta,\gamma\)均为非负的

  2. 求\(\alpha,\beta,\gamma\)：通过面积计算

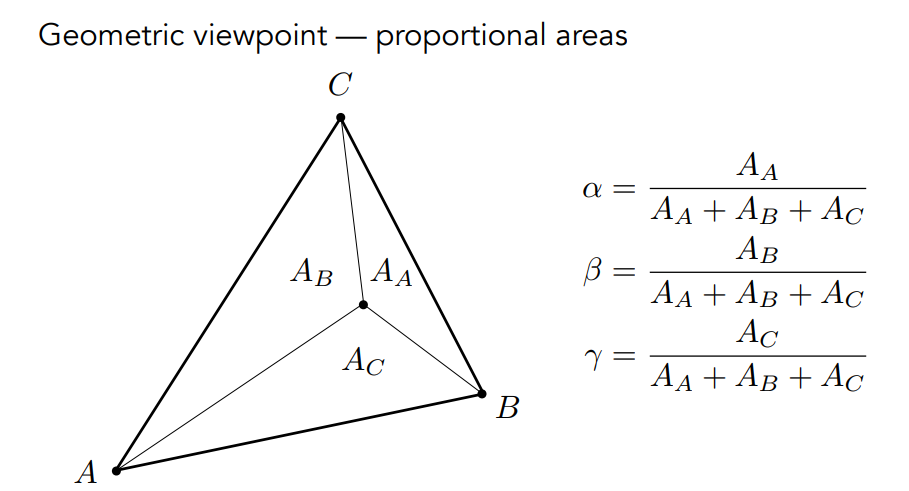
    image-20230320182149277

  3. 三角形的重心：分成的三个三角形面积相等

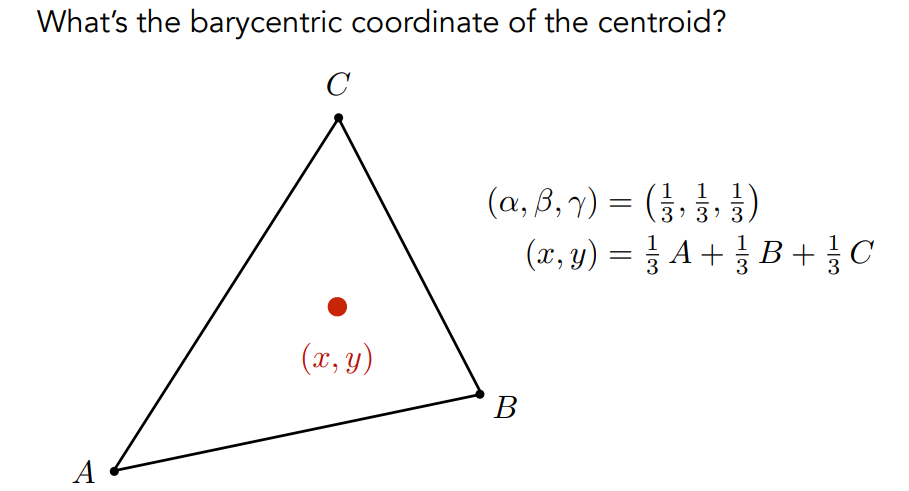
    image-20230320182314078

  4. 使用公式计算：

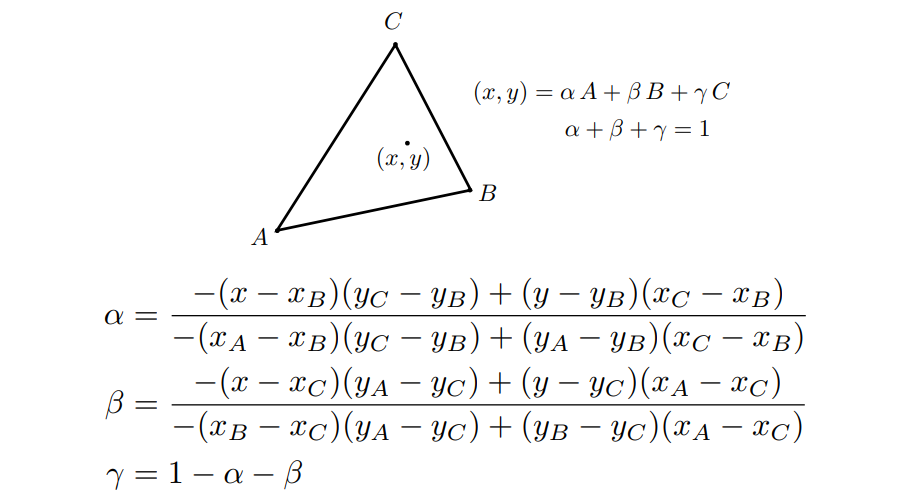
    image-20230320182412696

9.1.2 重心坐标插值

注意：投影后，重心坐标可能会改变，因此插值三维属性，应该使用三维坐标

image-20230320182502273

9.2 纹理的基础应用

9.2.1 简单纹理映射：漫反射颜色

对每一个屏幕中的采样点\((x,y)\)：

  1. 通过重心坐标插值，计算\((x,y)\)对应的纹理坐标\((u,v)\)
  2. 得到纹理中，\((u,v)\)所在点的颜色，记为texcolor = texture.sample(u,v)
  3. 将该采样点的颜色，设置为texcolor

9.2.2 纹理放大：双线性插值 Bilinear interpolation

像素pixel <=> 纹理元素texel，纹理需要放大时，多个pixel会对应到同一个texel上

纹理过小：失真

image-20230320184241753

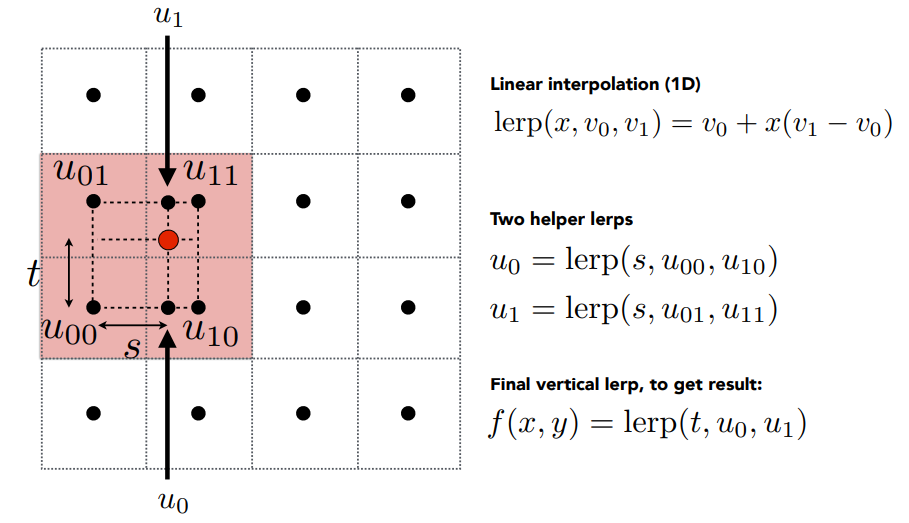
  1. 找到临近的四个点
  2. 计算水平距离s和垂直距离t，均为[0,1]之间的值
  3. 定义线性插值操作：\(lerp(x,v_0,v_1)=v_0+x(v_1-v_0)\)，\(x\)为[0,1]之间的值
  4. 进行两次线性插值操作：
    1. 水平方向：\(u_0=lerp(s,u_{00},u_{10}),u_1=lerp(s,u_{01},u_{11})\)
    2. 垂直方向：\(f(x,y)=lerp(t,u_0,u_1)\)

image-20230320183957812

9.2.3 纹理缩小

纹理过大：远处摩尔纹，近处锯齿

  1. 远处，一个像素覆盖了纹理上的很大一块区域，因此会存在走样

image-20230320184320810

9.2.3.1 Mipmap

Mipmap：允许做快速、近似、正方形的范围查询

  1. 每一层均将上一层缩小到原来的一半

    1. 预处理纹理
    2. 多了1/3的存储量

    image-20230320185053505

  2. 计算某个像素对应到纹理的正方形区域

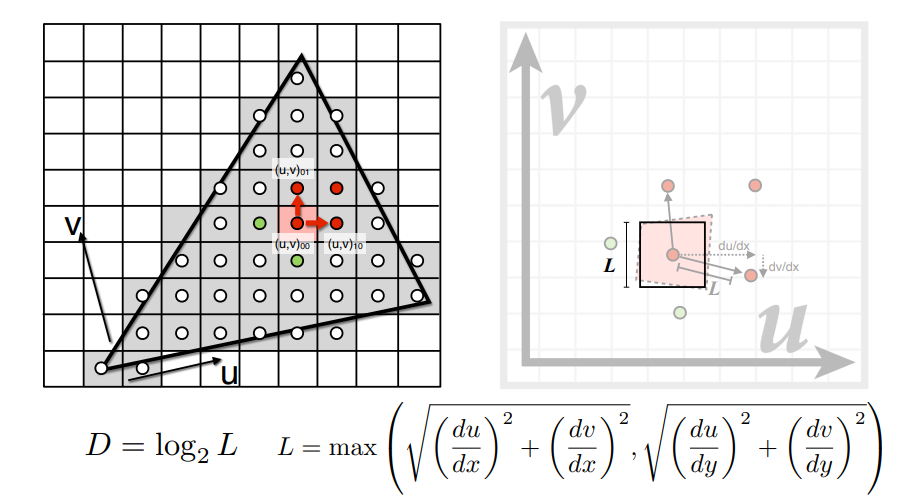
    1. 将屏幕上的某个像素点p1及其两个邻居p2,p3对应到纹理上的三个点t1,t2,t3
    2. 在屏幕上，p1与p2的距离为1，p1与p3的距离为1
    3. 在纹理中，t1与t2的距离为L1，t1与t2的距离为L2
    4. 取L=max(L1,L2)，则该像素在纹理空间上对应的正方形区域为，以t1为中心的L×L的区域

    image-20230320185714401

  3. 计算正方形区域的平均值

    1. 假设正方形为1×1，则可以直接在0层中获得该区域的平均值
    2. 假设正方形为4×4，则可以直接在1层中获得该区域的平均值
    3. 因此，我们可以在第\(D=log_2L\)层中获取该区域的平均值
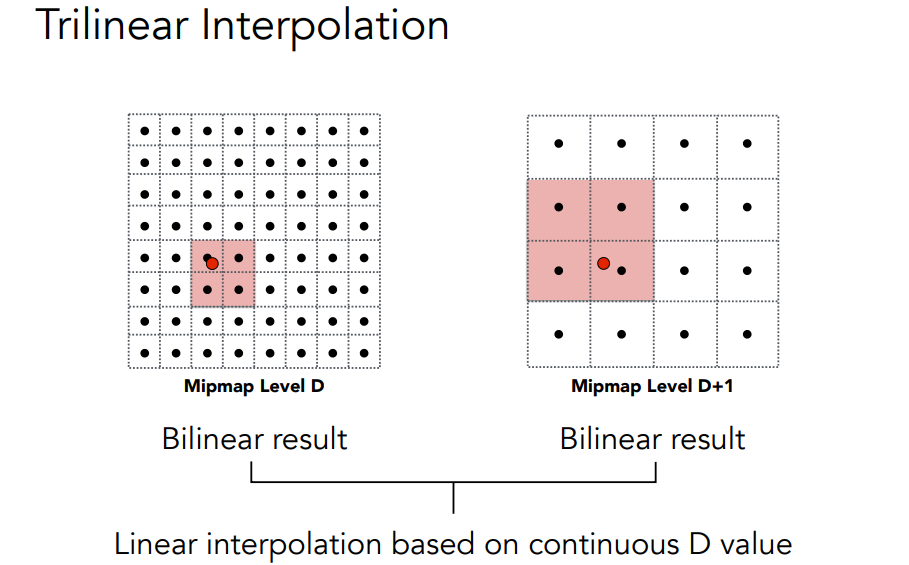
    4. 如果\(log_2L\)不是整数，则可以通过线性插值，获得该区域的平均值
    5. 每一层的查询，使用了一次双线性插值，最后又进行了一次线性插值，因此称为三线性插值

    image-20230320190152780

  4. 缺点：在远处会完全模糊overblur

9.2.3.2 各向异性过滤

Anisotropic Filtering：各向异性过滤，对矩形的区域快速查询平均值

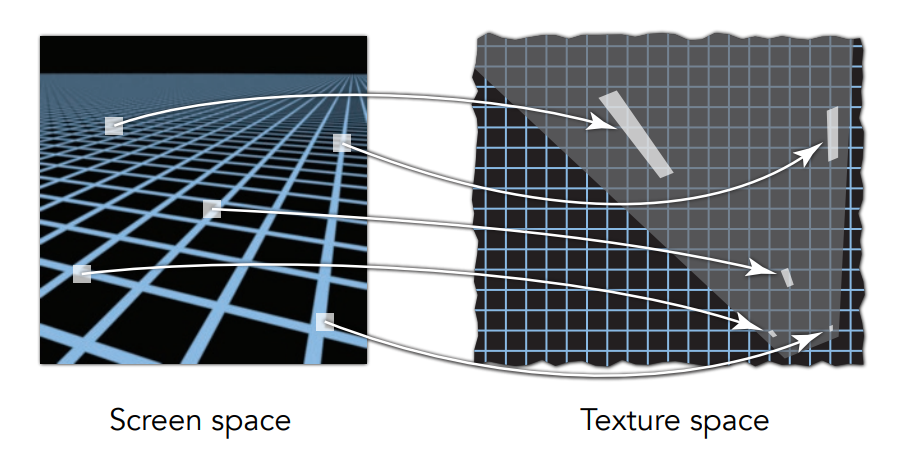
image-20230320190538811

  1. 各向异性过滤：水平、竖直压扁，开销为原本的3倍
  2. EWA过滤：将图像分为一个个的椭圆

image-20230320190625611

9.3 纹理的其他应用

现代GPU中，纹理的本质：是一块内存区域，且可以进行范围查询

9.3.1 环境贴图 Environment Map

  1. 环境贴图：即为空间中的某个点，向上下左右前后六个方向，所能接收到的光
  2. 可以通过环境贴图，进行光照计算，进而实现环境光渲染
  3. 基本假设：环境光来自无限远处，只记录环境光的方向信息
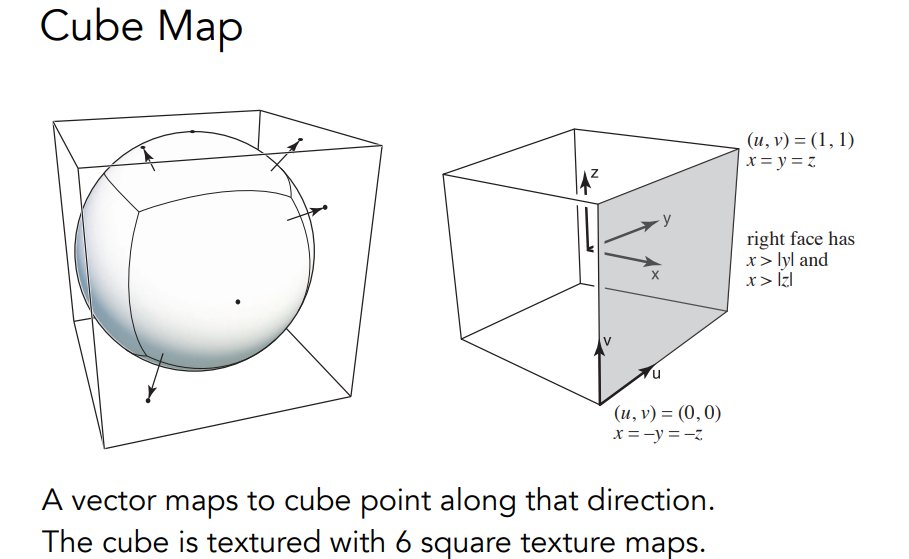
  4. 可以使用Spherical Map或者Cube Map表示

image-20230320203116579

image-20230320203423125

由于立方体的各个面都是均匀的，因此能很好的避免天空球的极点消失现象

  1. 天空盒只记录方向信息
  2. 需要先判断某个方向是属于哪一个面上的

image-20230320203303350

9.3.2 凹凸贴图 & 法线贴图

  1. 凹凸贴图：定义某个点的相对高度(沿法线移动的距离)，从而改变周围像素的法线方向
  2. 法线贴图：定义某个点的法线

image-20230320203552597

计算修改后的法线

  1. 一维贴图，修改像素的法线：flatland

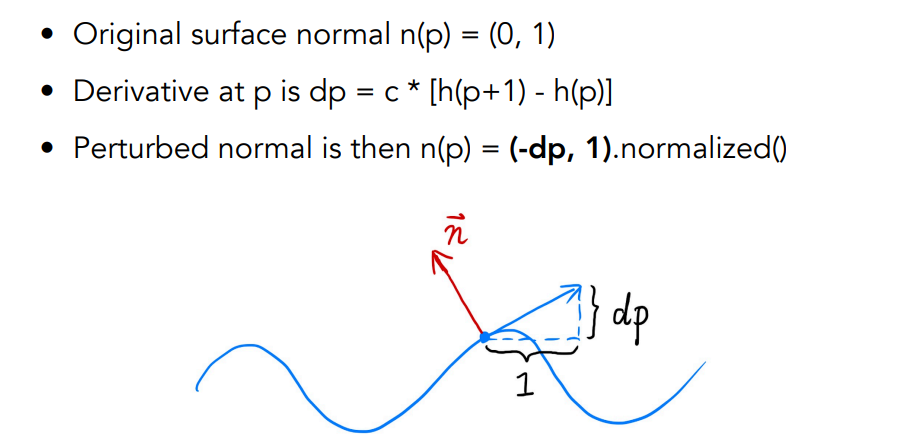
    1. 设原来的表面法线n(p)=(0, 1)
    2. 计算梯度：dp=c*[h(p+1)-h(p)]
    3. 则切线为：(1,dp)
    4. 因此更改后的法线为：n(p)=(-dp, 1).normalized()

    image-20230320203941915

  2. 二维贴图，修改像素的法线：局部坐标系下

    1. 设原来的表面法线n(p)=(0, 0, 1)
    2. 计算梯度：dp/du=c1*[h(u+1)-h(u)]，dp/dv=c2*[h(v+1)-h(v)]
    3. 因此更改后的法线为：n(p)=(-dp/du, -dp/dv ,1).normalized()

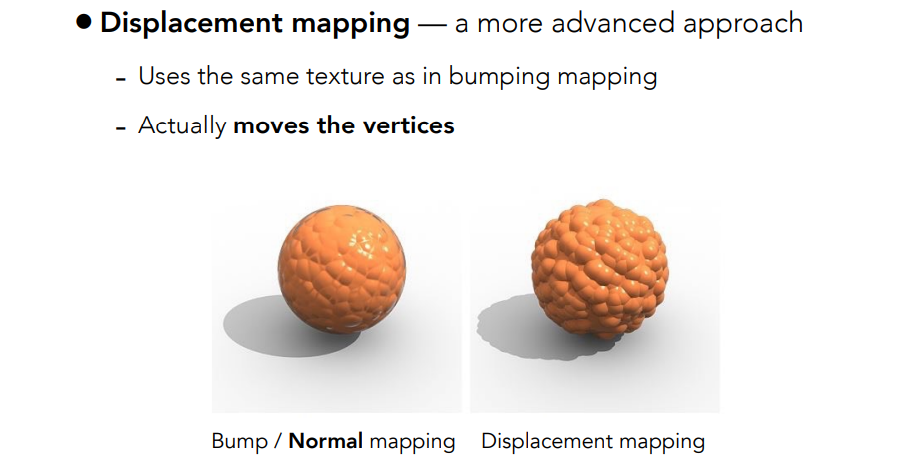
9.3.3 位移贴图 Displacement Mapping

  1. 与凹凸贴图类似，但是会直接更改三角形顶点的位置
  2. 要求原有模型的三角形比较细，要求模型的三角形顶点之间的间隔，比纹理之间的间隔小

image-20230320204818983

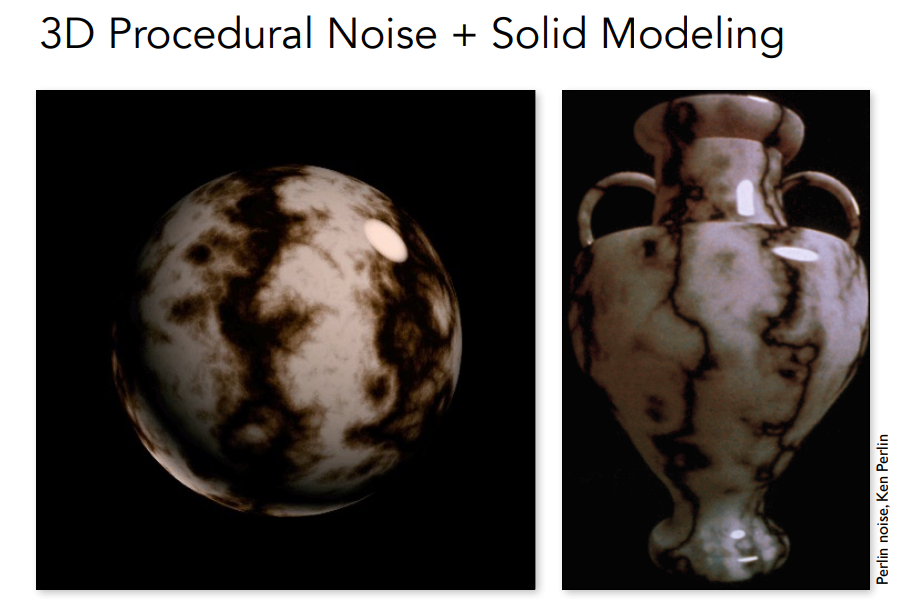
9.3.4 三维纹理

  1. 定义一个三维空间的噪声函数，可以得到三维空间中，任意一个点的属性

image-20230320205137485

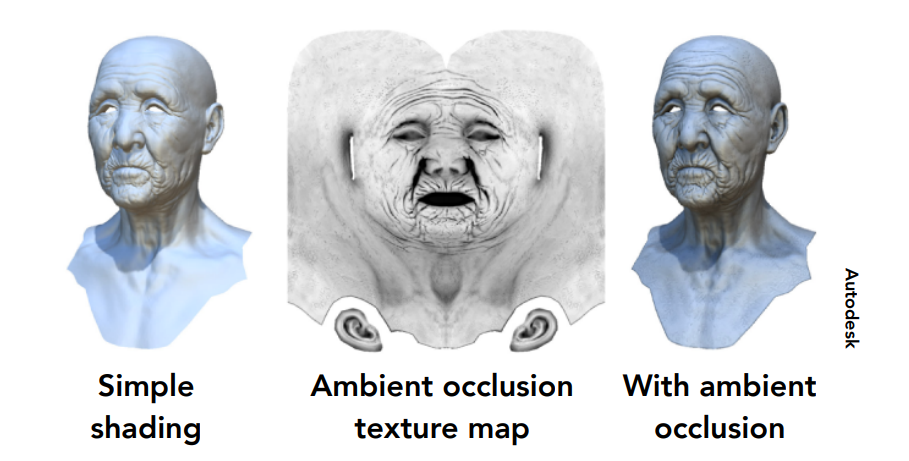
9.3.5 保存预处理的数据

image-20230320205230388

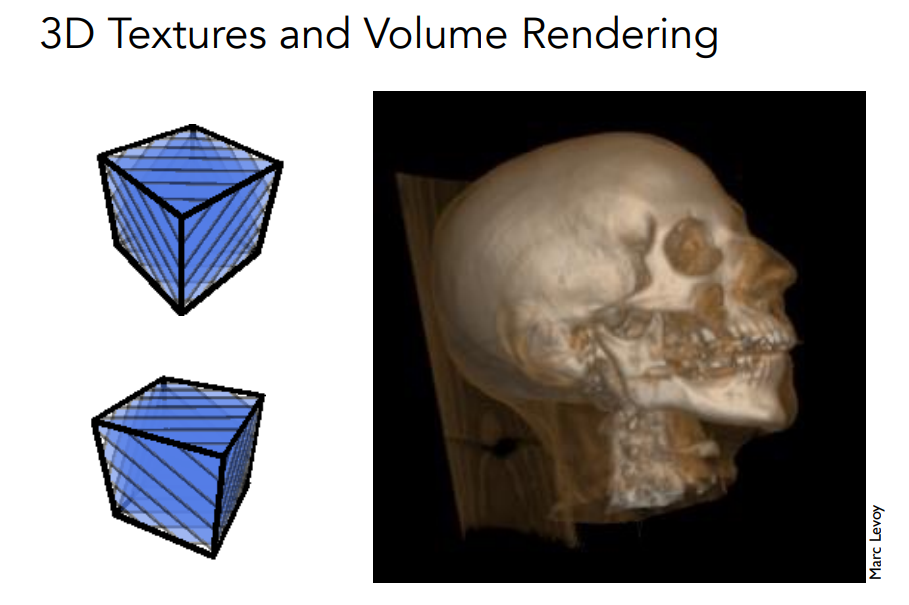
9.3.6 三维纹理 & 体积渲染

image-20230320205313633