十一、几何2：曲线和曲面

11.1 贝塞尔曲线 Bezier Curve

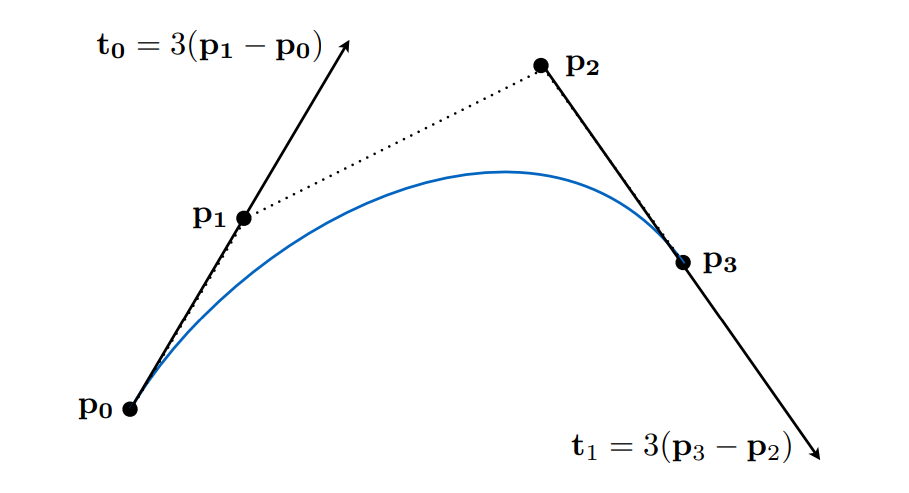
  1. 定义四个控制点p0,p1,p2,p3，要求曲线的起始切线方向为p1-p0，终止切线方向为p3-p2
  2. 曲线不一定经过控制点

image-20230320213504658

11.1.1 de Casteljau算法

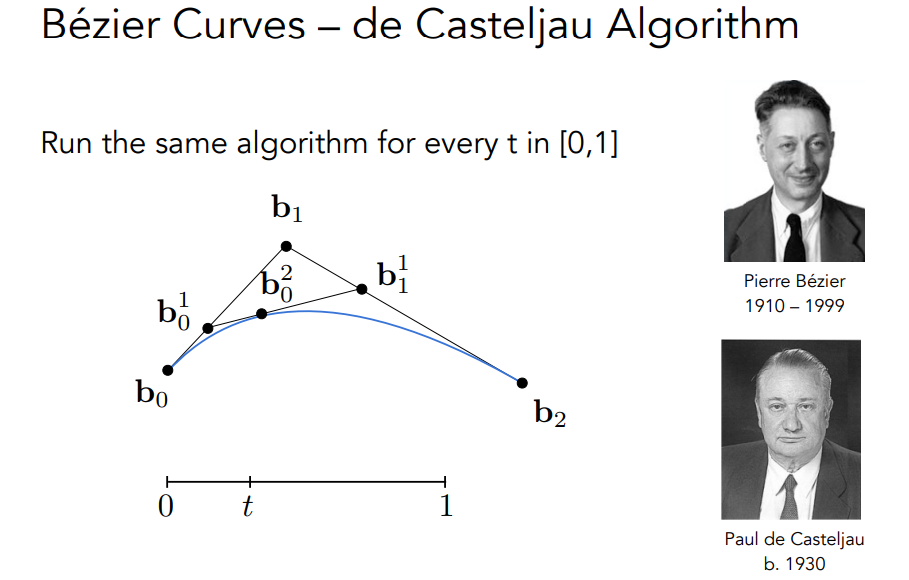
11.1.1.1 二次贝塞尔曲线：三个控制点

  1. b0为起点，b2为终点，b1控制曲线弯曲
  2. 实际上是：对于每一个时间t，找到当前时刻对应的点的坐标
    1. 第一步：
      1. 在\(b_0b_1\)上，设\(b_0\)为时间0，\(b_1\)为时间1，线性插值找到\(b_0^1\)
      2. 在\(b_1b_2\)上，设\(b_1\)为时间0，\(b_2\)为时间1，线性插值找到\(b_1^1\)
    2. 第二步：
      1. 在\(b_0^1b_1^1\)上，设\(b_0^1\)为时间0，\(b_1^1\)为时间1，线性插值找到\(b_0^2\)
    3. 则\(b_0^2\)记为贝塞尔曲线，在时间t所在的位置

image-20230320214216113

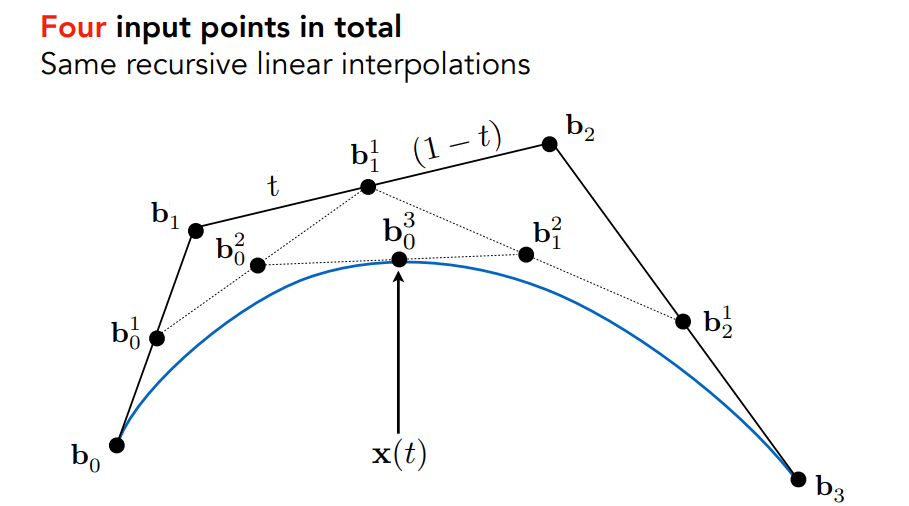
11.1.1.2 四个控制点

  1. b0为起点，b3为终点，b1,b2控制曲线弯曲
  2. 实际上是：对于每一个时间t，找到当前时刻对应的点的坐标
    1. 第一步：
      1. 在\(b_0b_1\)上，设\(b_0\)为时间0，\(b_1\)为时间1，线性插值找到\(b_0^1\)
      2. 在\(b_1b_2\)上，设\(b_1\)为时间0，\(b_2\)为时间1，线性插值找到\(b_1^1\)
      3. 在\(b_2b_3\)上，设\(b_2\)为时间0，\(b_3\)为时间1，线性插值找到\(b_2^1\)
    2. 第二步：
      1. 在\(b_0^1b_1^1\)上，设\(b_0^1\)为时间0，\(b_1^1\)为时间1，线性插值找到\(b_0^2\)
      2. 在\(b_1^1b_2^1\)上，设\(b_1^1\)为时间0，\(b_2^1\)为时间1，线性插值找到\(b_1^2\)
    3. 第三步：
      1. 在\(b_0^2b_1^2\)上，设\(b_0^2\)为时间0，\(b_1^2\)为时间1，线性插值找到\(b_0^3\)
    4. 则\(b_0^3\)记为贝塞尔曲线，在时间t所在的位置x(t)

image-20230320214234859

11.1.1.3 贝塞尔曲线的代数形式

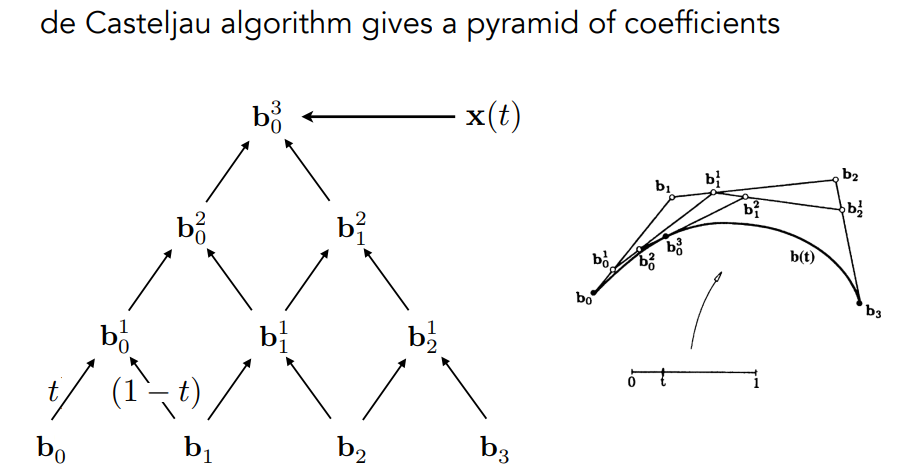
image-20230320214621950

2阶贝塞尔曲线

image-20230320214734581

11.1.2 n阶贝塞尔曲线的代数表示

参数为 (1-t+t)n 的多项式展开

\[ b^n(t) = \sum_{j=0}^n b_j B_j^n(t) \]

  1. \(b^n(t)\)：n阶贝塞尔曲线的表达式
  2. \(b_j\)：第j个控制点，可以为三维空间中的点
  3. \(B_j^n(t)\)：Bernstein多项式，此处为\(C_{n}^i\ t^i\ (1-t)^{n-i}\)

11.1.3 贝塞尔曲线的性质

  1. 必须过起点和终点：\(b(0)=b_0,b(1)=b_n\)

  2. 对于三阶贝塞尔曲线：\(b'(0)=3(b_1-b_0),b'(1)=3(b_3-b_2)\)

  3. 在仿射变换中：对贝塞尔曲线的仿射变换 <=> 对控制点做仿射变换然后再计算贝塞尔曲线

    1. 但是对投影变换不行

  4. 凸包性质：贝塞尔曲线一定在控制点形成的凸包内

    1. 凸包：包围某些顶点的最小凸多边形

      可以将顶点想象为钉子，用橡皮筋包裹住所有顶点，然后松手，橡皮筋最后的形状记为这些顶点的凸包

    2. 如果控制点在同一条直线上，则贝塞尔曲线就是这条直线

11.1.4 分段贝塞尔曲线 Picewise Bezier Curves

  1. 通常为4个控制点，控制一段贝塞尔曲线

  2. PS中的钢笔工具，就应用了分段贝塞尔曲线

    image-20230320220627770

  3. 保证连续（C0连续）：

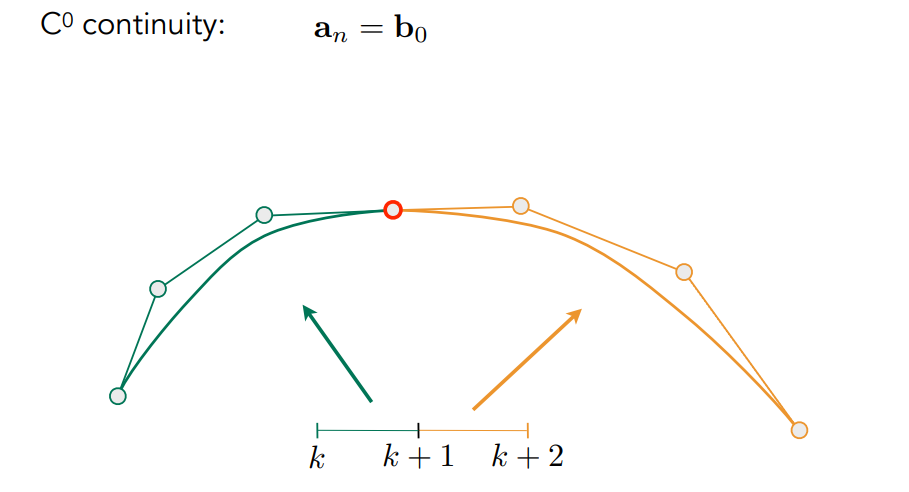
    image-20230320221118919

  4. 保证光滑/切线连续（C1连续）：相邻的两端贝塞尔曲线中，上一段曲线的最后两个控制点，与下一段曲线的最初两个控制点，共线且距离相同

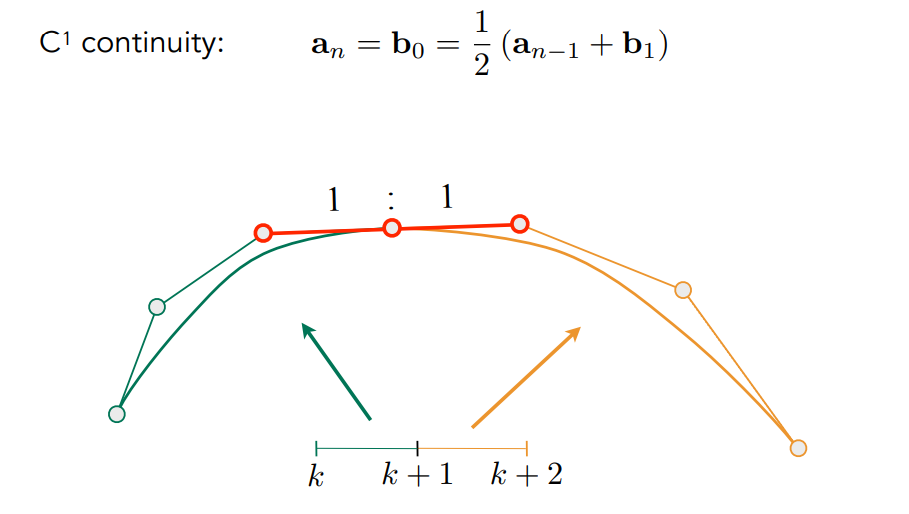
    image-20230320221132408

11.2 样条曲线 Spline

样条：一个可控的曲线

11.2.1 B样条 Basis-Spline

基函数样条

  1. 贝塞尔曲线，既可以理解为用Bernstein多项式，对控制点加权求和；也可以理解为用控制点，对Bernstein多项式进行加权求和。则Bernstein多项式，即为基函数
  2. 相当于由不同的函数，通过某一种方式结合起来，得到另一个函数
  3. B样条是对贝塞尔曲线的扩展，可以保证修改的局部性，改变一个点，至多影响曲线的某个部分

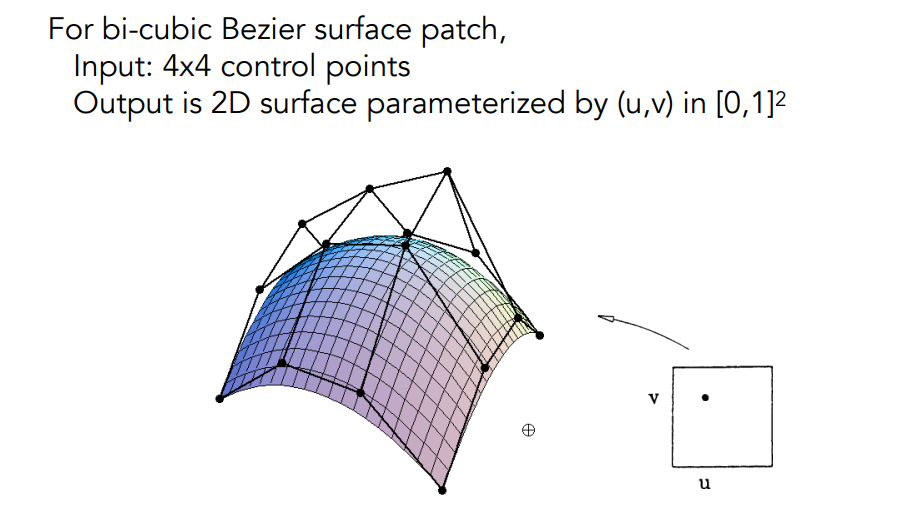
11.3 贝塞尔曲面 Bezier Surfaces

11.3.1 4×4个控制点

  1. 对于每一行的4个控制点，计算每一行的贝塞尔曲线

  2. 对于每一个时间t1，对应的4行贝塞尔曲线上的点，认为是4个控制点，可以得到另一个贝塞尔曲线，其时间为t2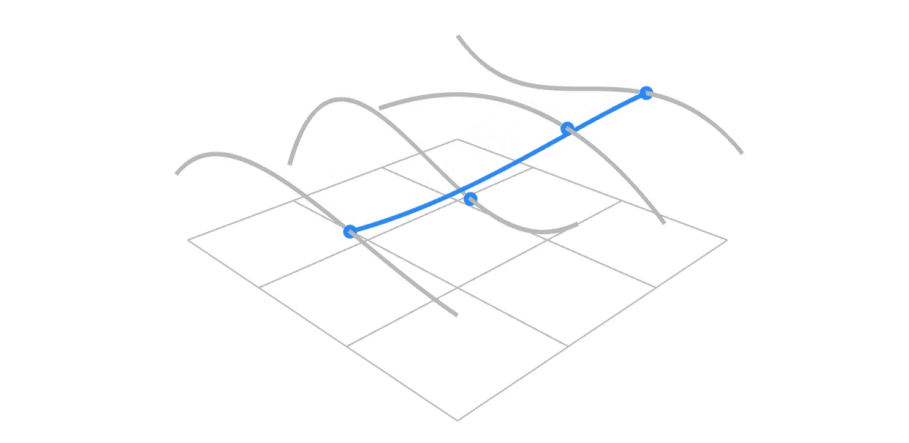

    image-20230320222831716

  3. 在t1,t2的变换过程中，即可得到贝塞尔曲面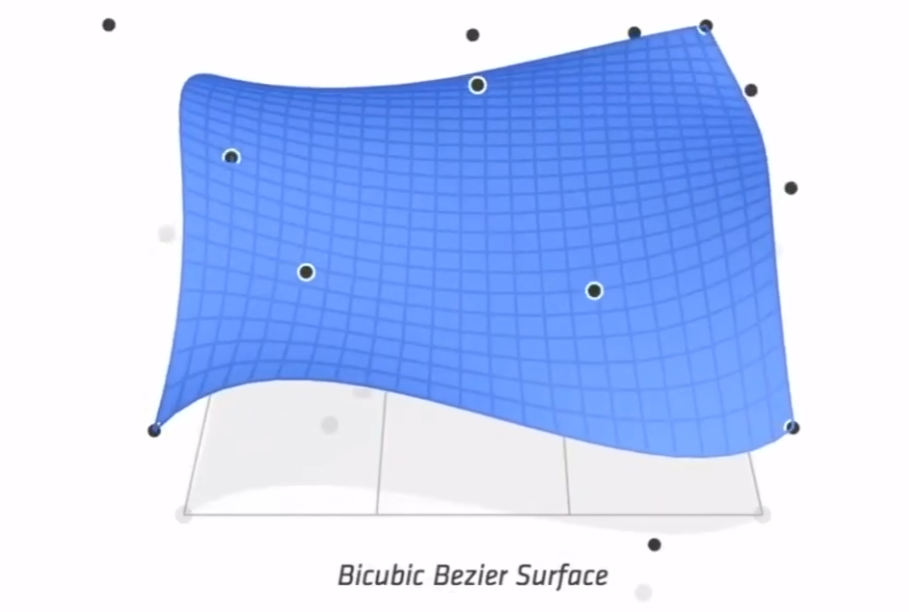

    image-20230320222940089

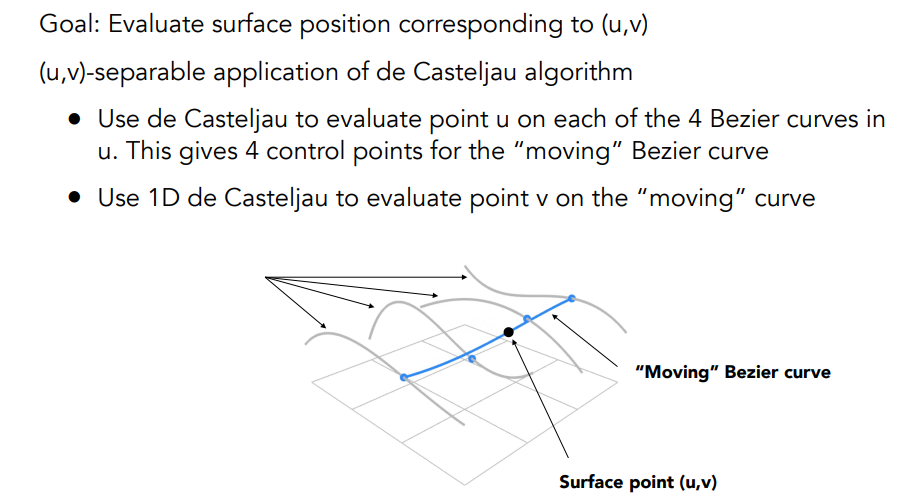
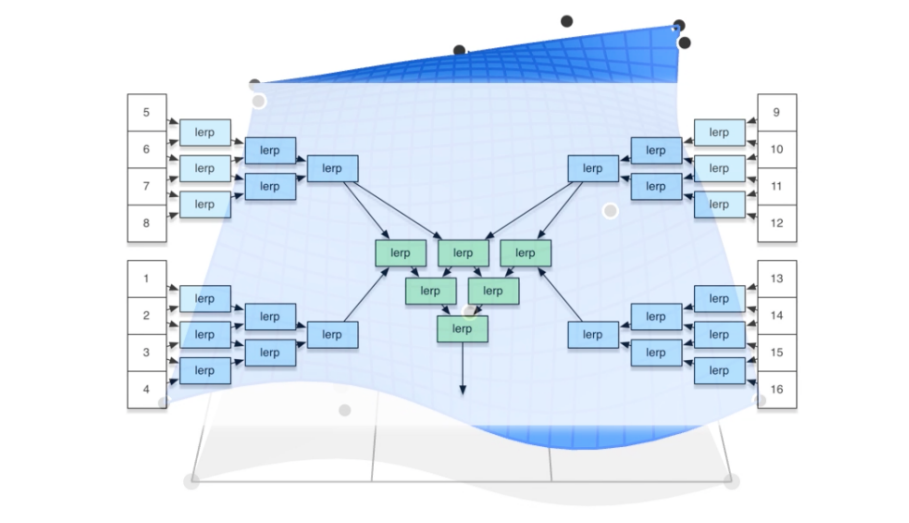
11.3.2 计算贝塞尔曲面

可以将参数(u,v)，映射到曲面上的对应点，因此贝塞尔曲面是显示表示

image-20230320223338990

image-20230320223409877

image-20230320223417719