GAMES101-16:光线追踪4:蒙特卡洛积分 & 路径追踪
十六、光线追踪4:蒙特卡洛积分 & 路径追踪
16.1 复习
渲染方程:描述了光线的传递
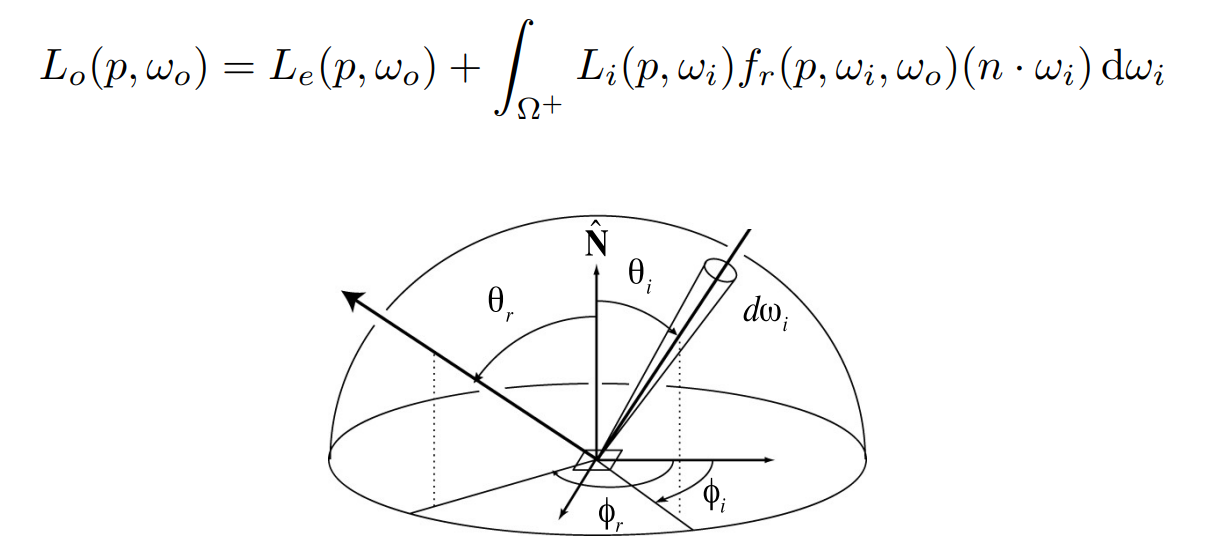
- 存在积分
- 是一个递归的计算:因为入射光可能是其他面的反射光
16.2 蒙特卡洛积分:采样求定积分
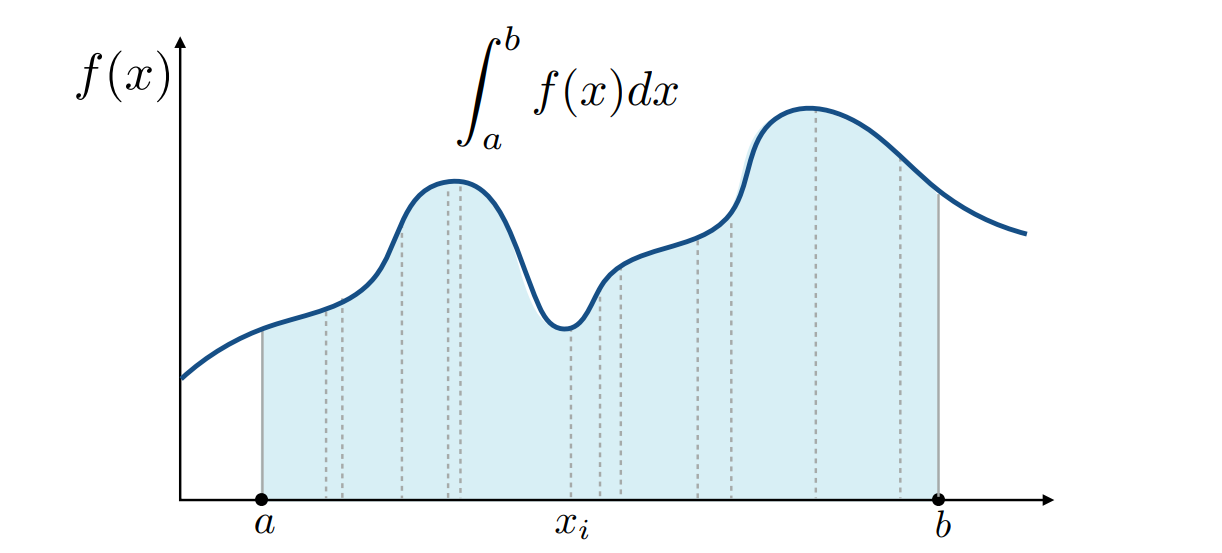
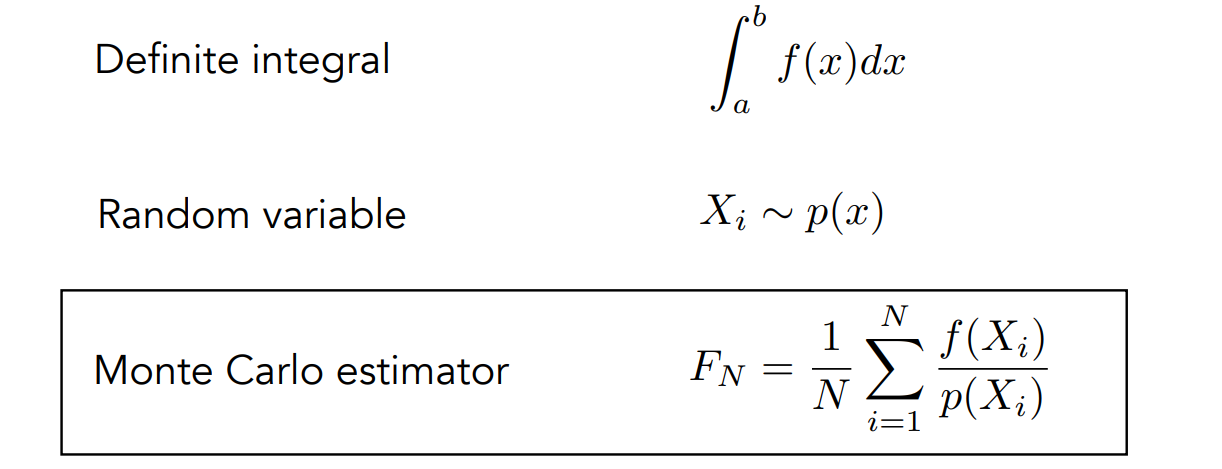
- 在\([a,b]\)中采样多次,设每次采样点为\(x_i\),对应的函数值为\(f(x_i)\),则使用\((b-a)*f(x_i)\),近似定积分的值
- 当采样次数足够多时,求平均值,即可得到实际的定积分的值
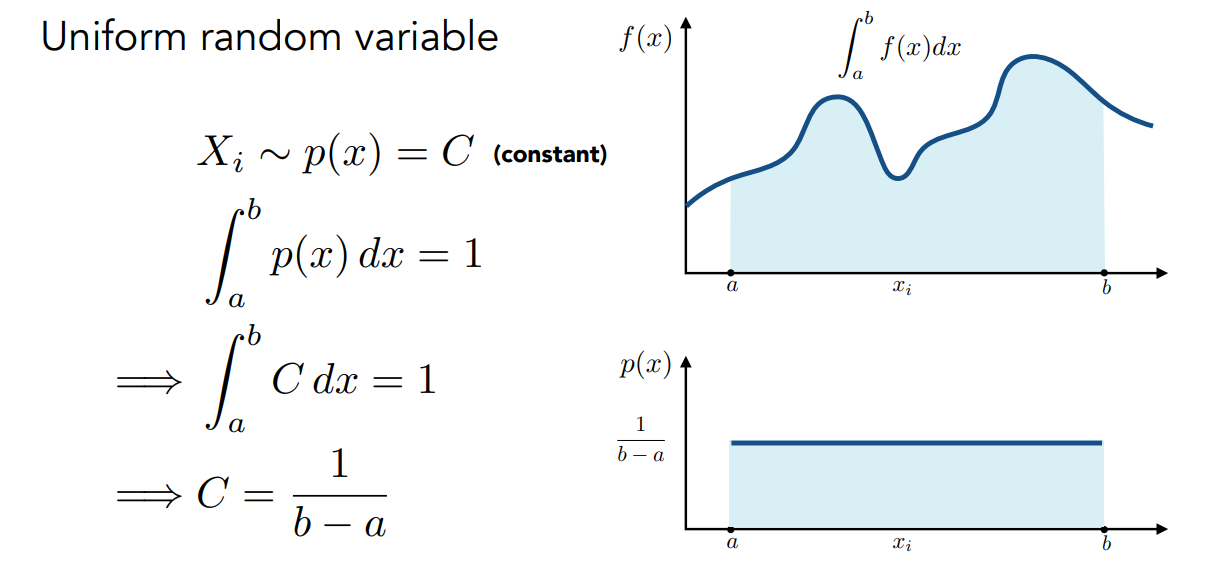
- 设随机采样点\(X_i\) ~ \(p(x)\),要求\(\int_{a}^b p(x)=1\),则蒙特卡洛的积分值为:\(F_N=\frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)}\)
示例:用\(X_i\) ~ \(p(x)\) = C采样
注意:
- 采样次数越多,结果越精确
- 在x上采样,则就是在x上积分
16.3 路径追踪:Path Tracing
16.3.1 Whitted-Style Ray Tracing 的做法存在的问题
不断的弹射光线,在任意一个位置均弹射光线
- 如果是光滑物体:则沿镜面方向反射、折射方向折射
- 如果是漫反射物体:停止弹射
存在问题:
- 对于glossy物体,不能按照specular那样的镜面反射处理
- 漫反射物体会将光线均匀的弹射到各个部分,而非不反射
16.3.2 使用蒙特卡洛积分,实现渲染方程中的积分

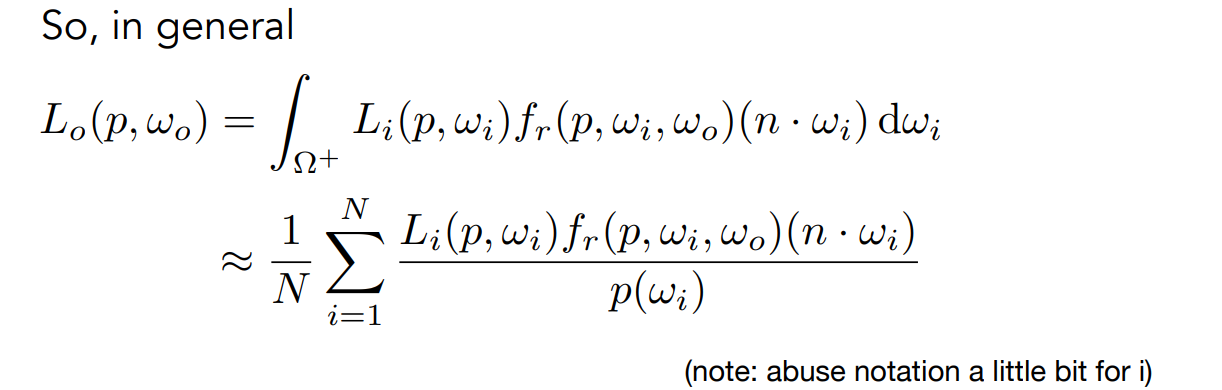
16.3.2.1 直接光照
shade(p, ωo)
- 随机选择N个方向,N的分布满足某一种PDF
- Lo初始化为0.0
- 对于每一个方向ωi
- 追踪光线r(p, ωi)
- 如果光线r击中了光源
- Lo += (1/N) * Li * fr * cos θ / PDF(ωi)
- 返回Lo
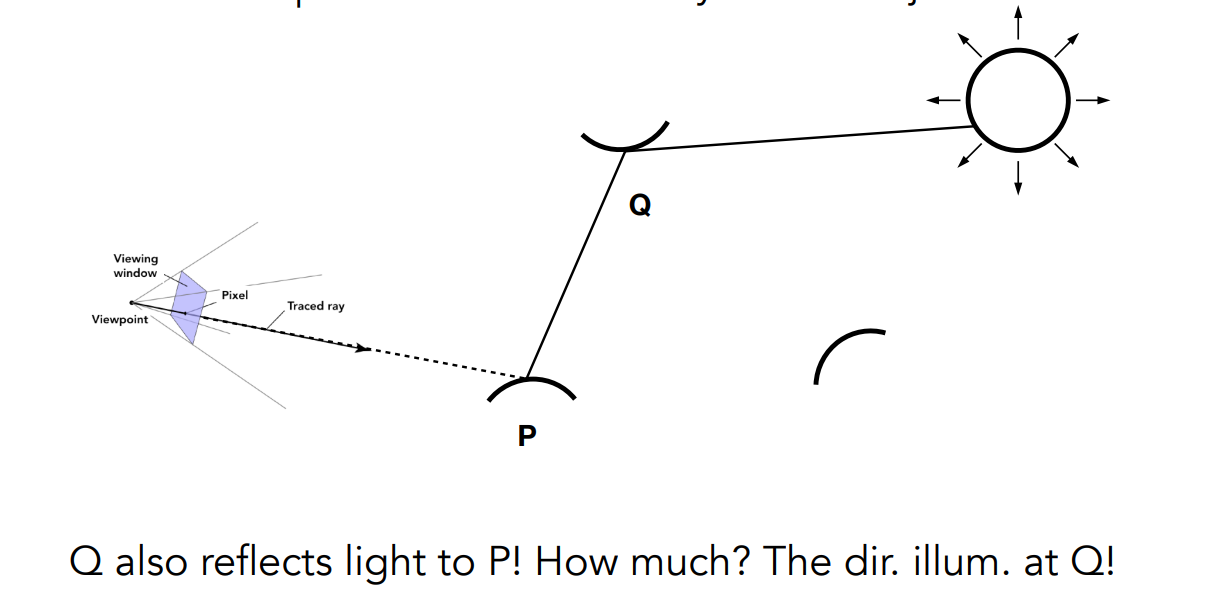
16.3.2.2 间接光照
相当于从P点看Q点的直接光照
shade(p, ωo)
- 随机选择N个方向,N的分布满足某一种PDF
- Lo初始化为0.0
- 对于每一个方向ωi
- 追踪光线r(p, ωi)(p点发出,方向为ωi)
- 如果光线r击中了光源
- Lo += (1/N) * Li * fr * cos θ / PDF(ωi)
- 如果光线r击中了物体,且物体位于q
- Lo += (1/N) * shade(q, -ωi) * fr * cos θ / PDF(ωi)
- 返回Lo
16.4 路径追踪:解决光线数量爆炸
问题:光线的数量会爆炸:光线数量 = N 反射次数,只有当N = 1时,才不会指数爆炸 ==> 路径追踪

16.4.1 每一个着色点,只使用1根光线进行追踪
shade(p, ωo)
- 随机选择1个方向ωi,ωi的分布满足某一种PDF
- 追踪光线r(p, ωi)(p点发出,方向为ωi)
- 如果光线r击中了光源
- 返回 Lo = Li * fr * cos θ / PDF(ωi)
- 如果光线r击中了物体,且物体位于q
- 返回 Lo = shade(q, -ωi) * fr * cos θ / PDF(ωi)
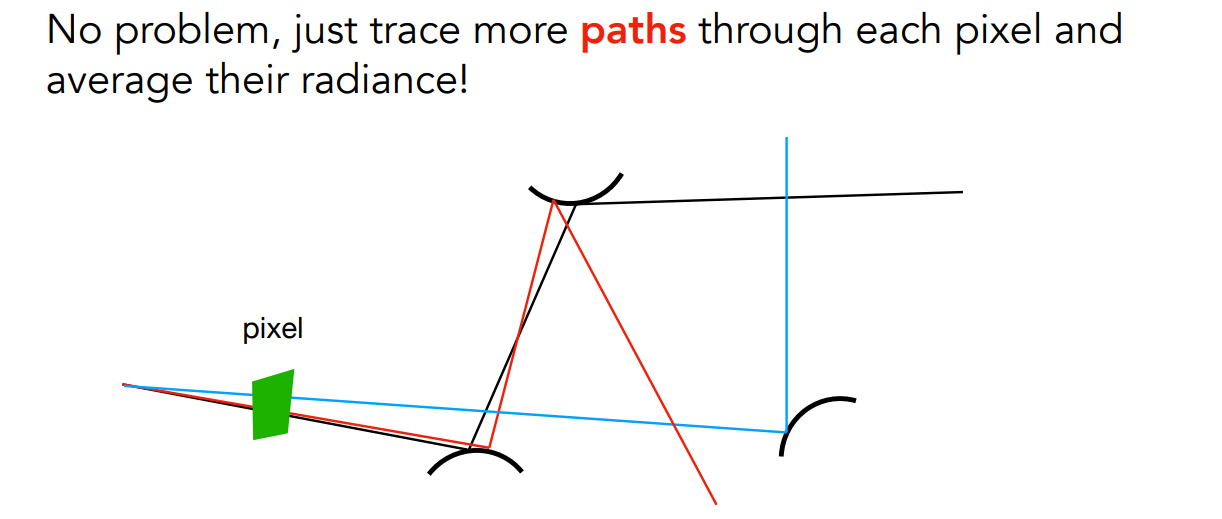
16.4.2 解决噪声问题:选择多个穿过该着色点的路径,每个路径1条光线
ray_generation(camPos, pixel)
- 在该像素中,随机选择N个采样位置
- pixel_radiance = 0.0
- 对于每一个采样位置
- 追踪光线r(camPos, cam_to_sample)
- 如果光线r在p点击中场景
- pixel_radiance += (1/N) * shade(p, sample_to_cam)
- 返回pixel_radiance
16.4.3 解决递归无法停下问题:Runssian Roulette
问题:shade(p, ωo)是递归定义的,可能无法停下 ==> RR,一定概率停止追踪
- 定义一个概率P
- P的概率,发射一个光线,并且返回Lo / P
- 1-P的概率,不发射光线,返回0
- 最后的期望依旧为Lo

shade(p, ωo)
- 定义概率P_RR
- 随机生成一个在[0,1]的实数dist, 如果dist>P_RR,则返回0.0
- 随机选择1个方向ωi,ωi的分布满足某一种PDF
- 追踪光线r(p, ωi)(p点发出,方向为ωi)
- 如果光线r击中了光源
- 返回 Lo = Li * fr * cos θ / PDF(ωi) / P_RR
- 如果光线r击中了物体,且物体位于q
- 返回 Lo = shade(q, -ωi) * fr * cos θ / PDF(ωi) / P_RR
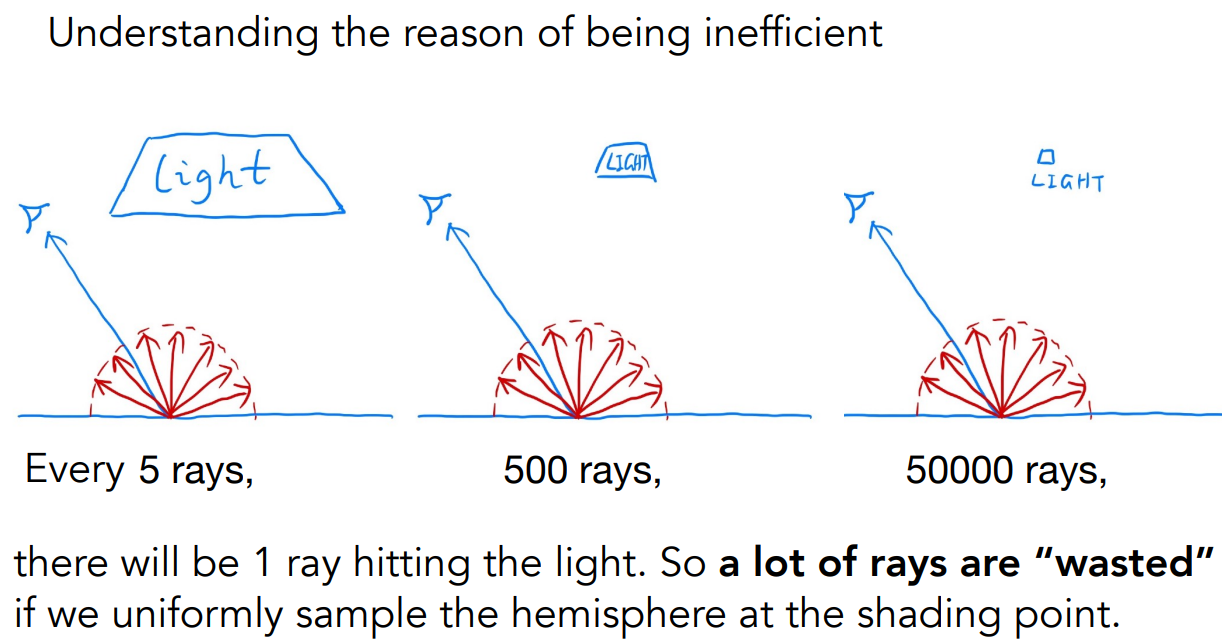
16.4.4 让路径追踪变得高效:对光源采样
均匀采样,导致很多光线无法打到小的光源,导致浪费计算力
对光源进行采样,然后将渲染方程修改为对光源的积分:即找到 dω 与 dA 的关系

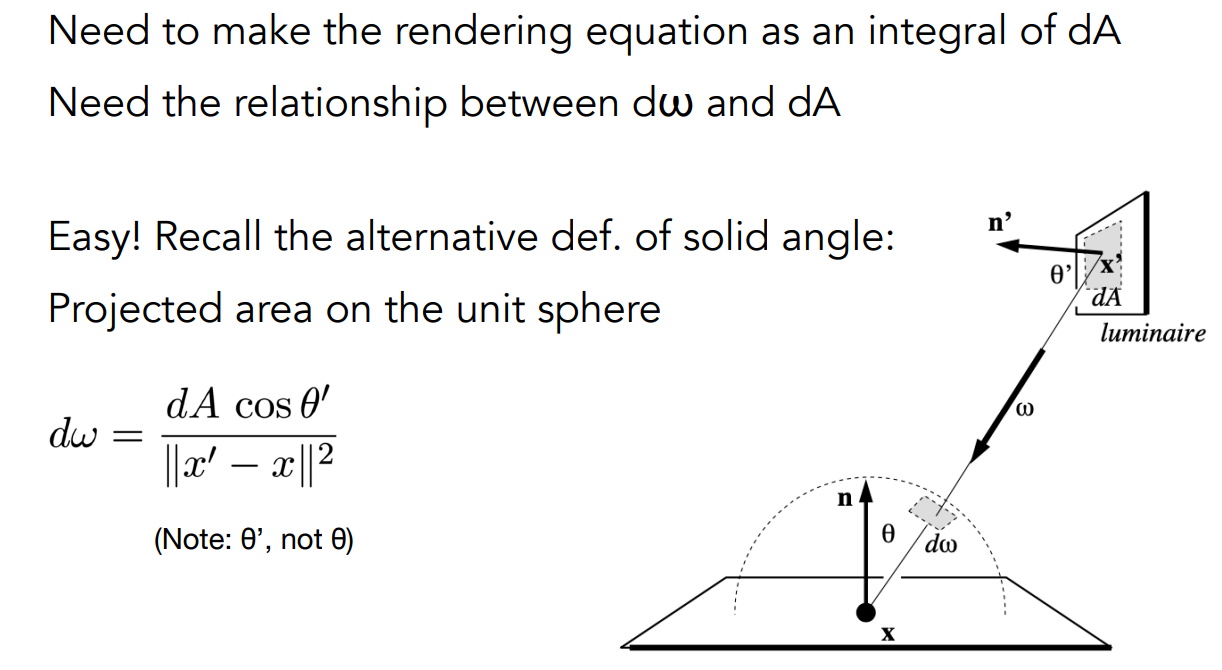
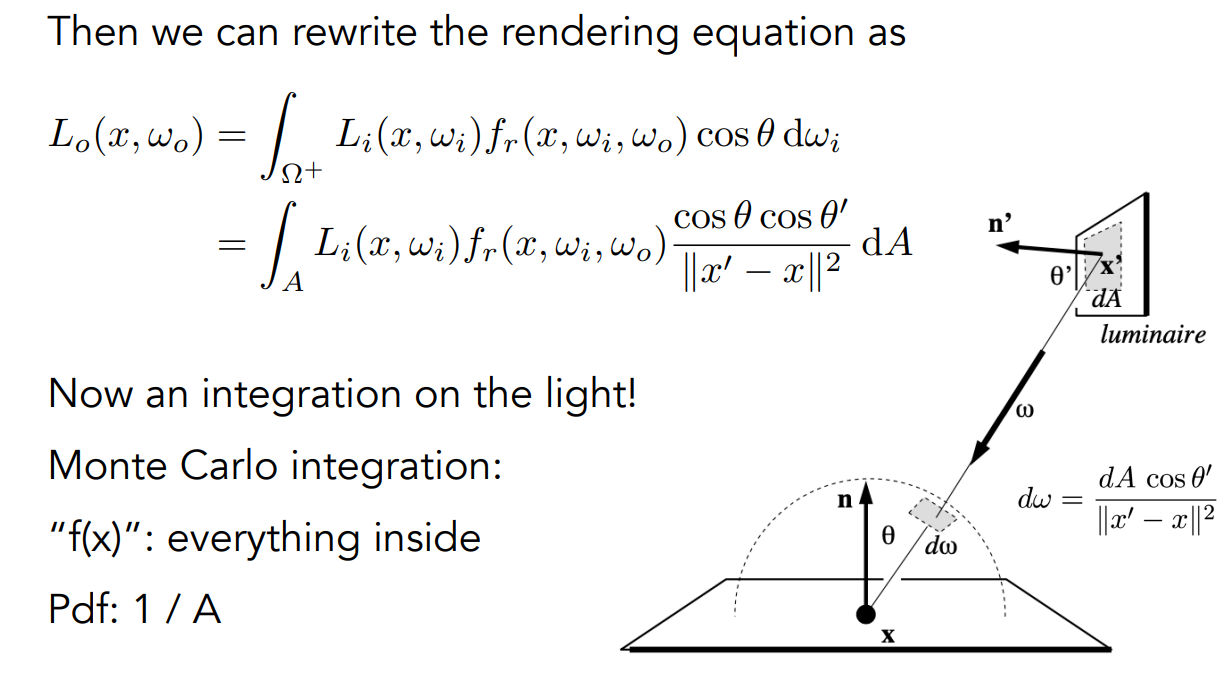
优化算法
将radiance分为两个部分:
- 来自光源的radiance:直接采样光源
- 其他反射光:使用RR的方法

shade(p, ωo)
光源的贡献
- 均匀的对位于x'的光源进行采样,PDF_light = 1 / A
- 从p向x'发射一条光线,如果光线不会被阻挡,则
- L_dir = Li * fr * cos θ * cos θ‘ / |x' - p|2 / PDF_light
其他反射光的贡献
- L_indir = 0.0
- 判断是否需要采样,RR的概率为P_RR
- 均匀的对半球进行采样,方位角为ωi,PDF_hemi = 1 / 2Π
- 追踪光线r(p, ωi)(p点发出,方向为ωi)
- 如果光线r击中了非发光体,且物体位于q
- L_indir = shade(q, -ωi) * fr * cos θ / PDF_hemi / P_RR
- 返回L_dir + L_indir
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 华风夏韵!
评论