GAMES101-17:材质与外观
十七、材质与外观
17.1 材质 == BRDF + BTDF= BSDF
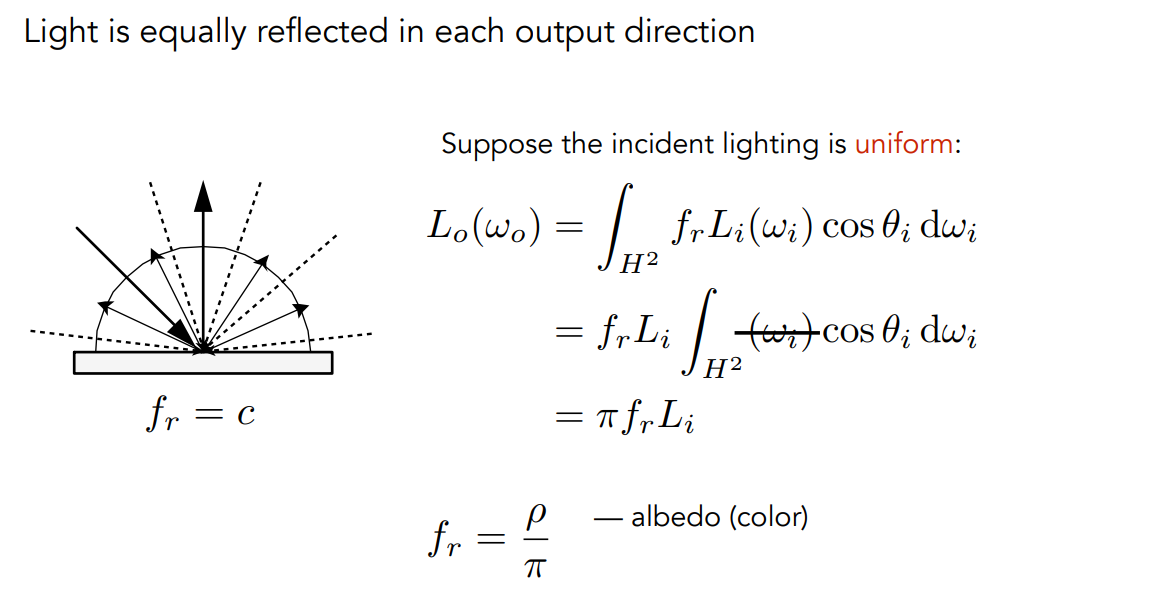
17.1.1 漫反射材质 BRDF
- 光线会被均匀的反射到每个方向
- 完全不吸收能量、不发光的漫反射材质:\(f_r=\frac{\rho}{\pi} \in[0,\frac{1}{\pi}]\)
- 其中\(\rho \in [0,1]\),表示对光的反射率
17.1.2 镜面反射 BRDF
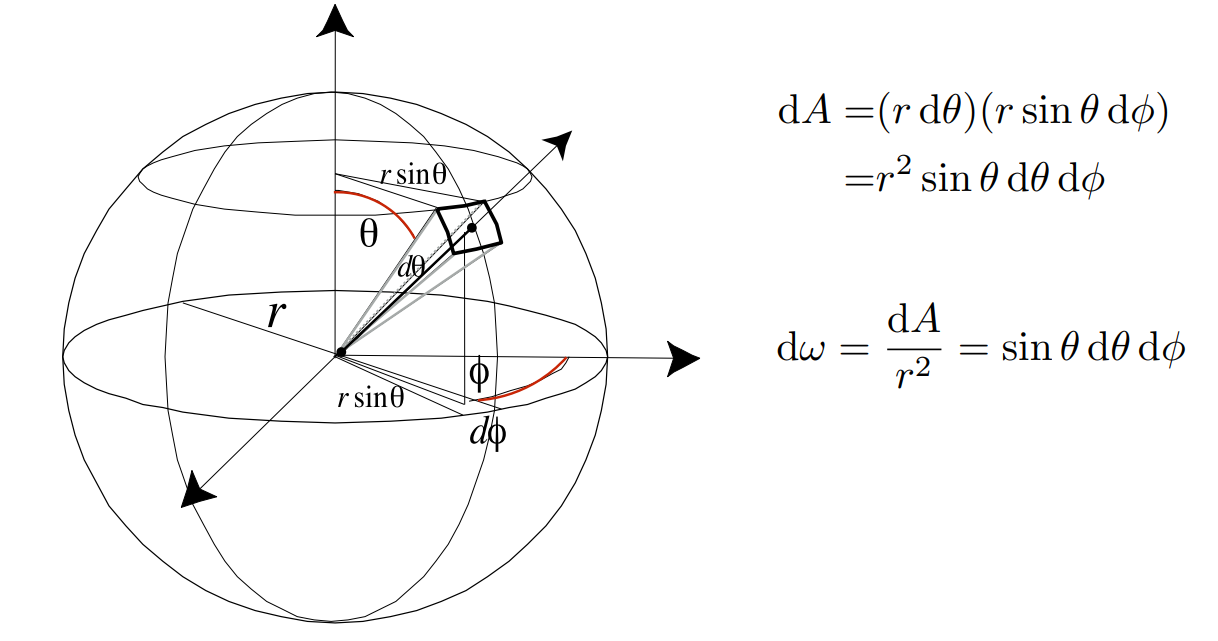
- 将入射光、反射光、平面放到立体角中
- 立体角坐标轴的Z轴方向为法线方向,XY平面为物体表面
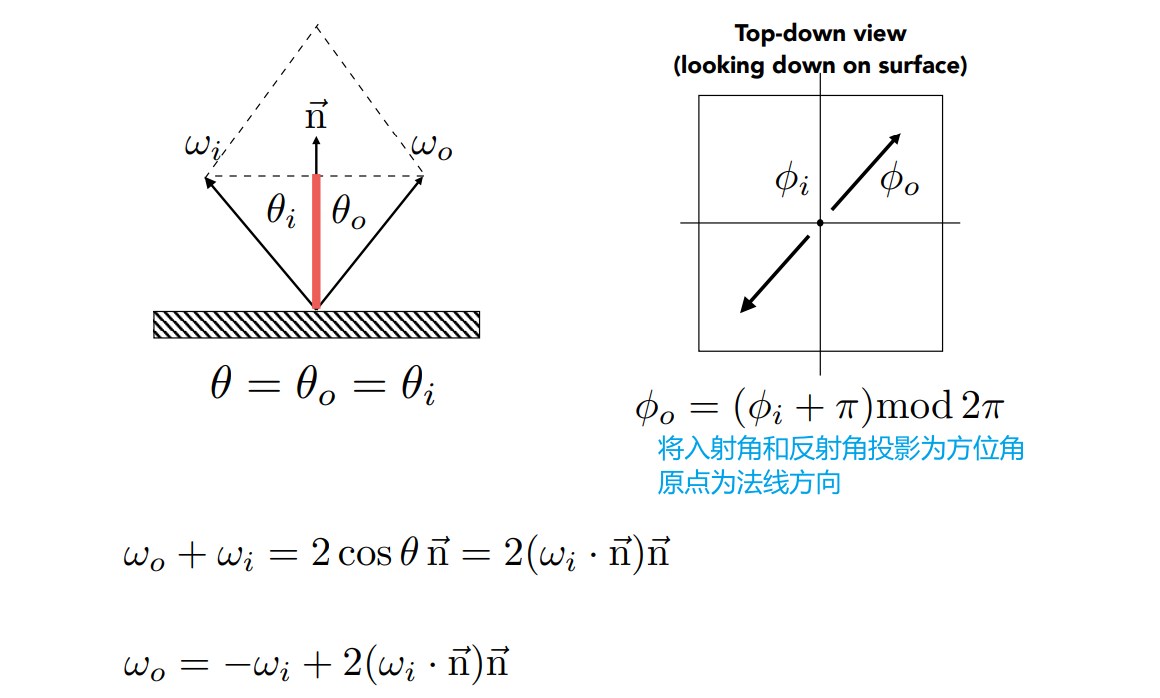 -
-
17.1.3 折射 BTDF
- 使用折射定律,算出反射角对应的\(\theta\)
- 然后通过方位角,求解对应向量
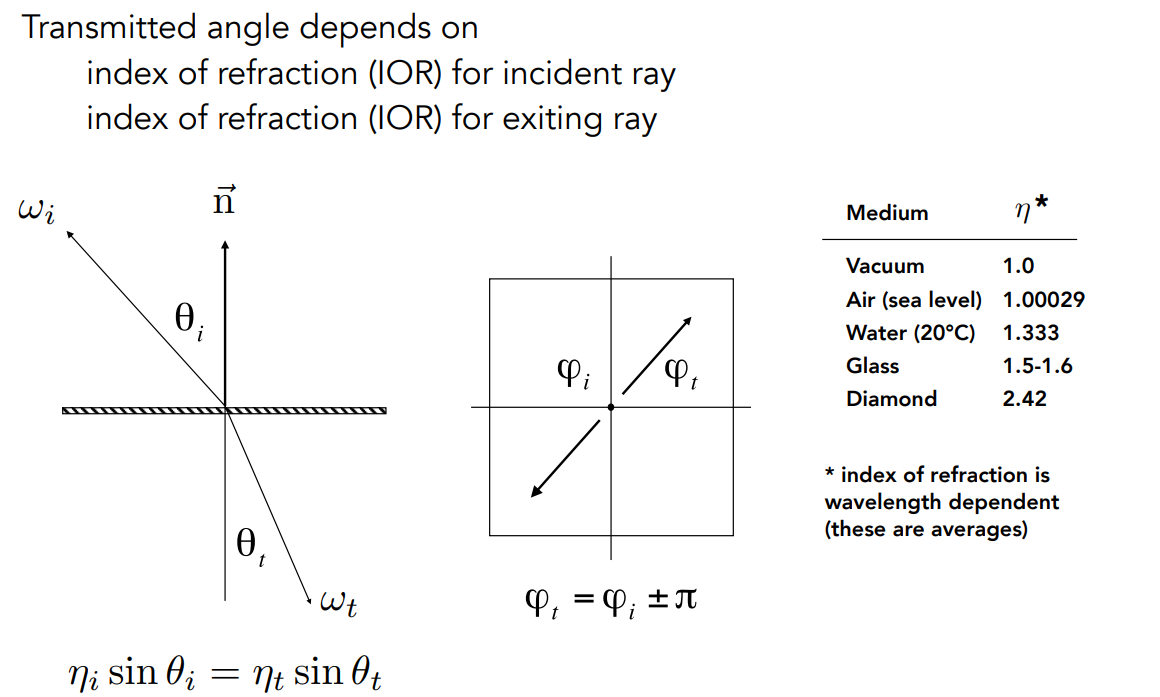
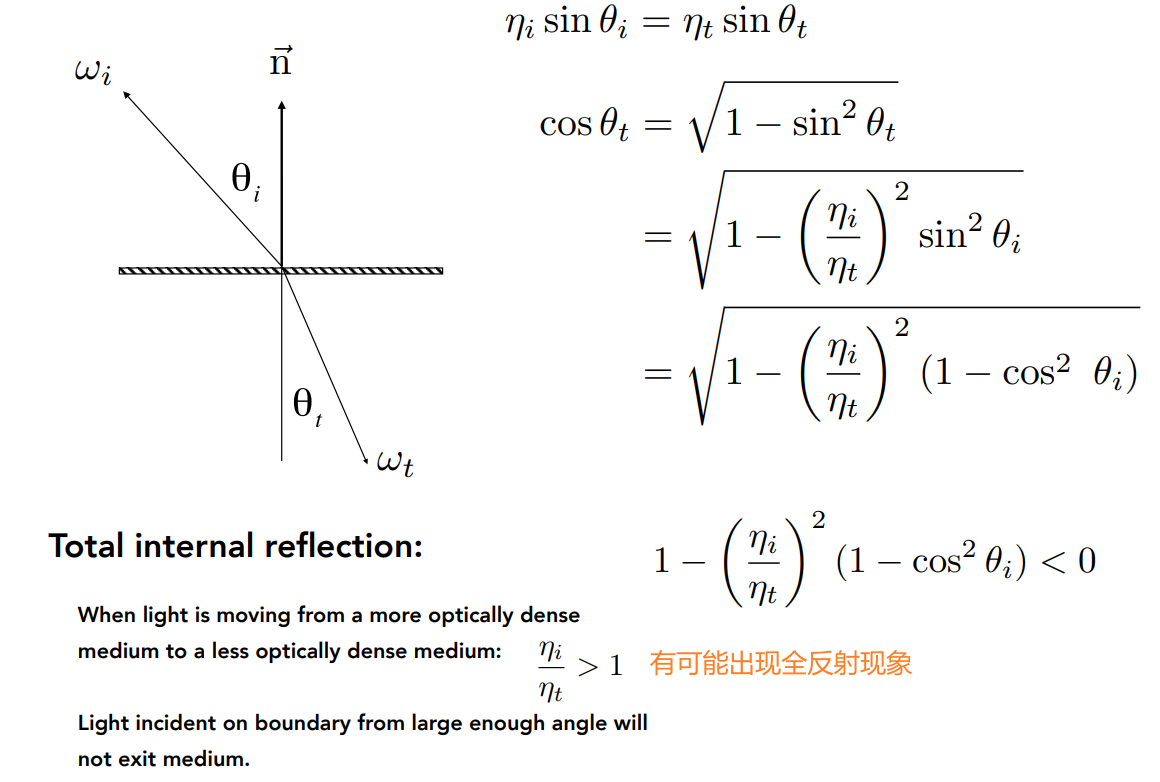
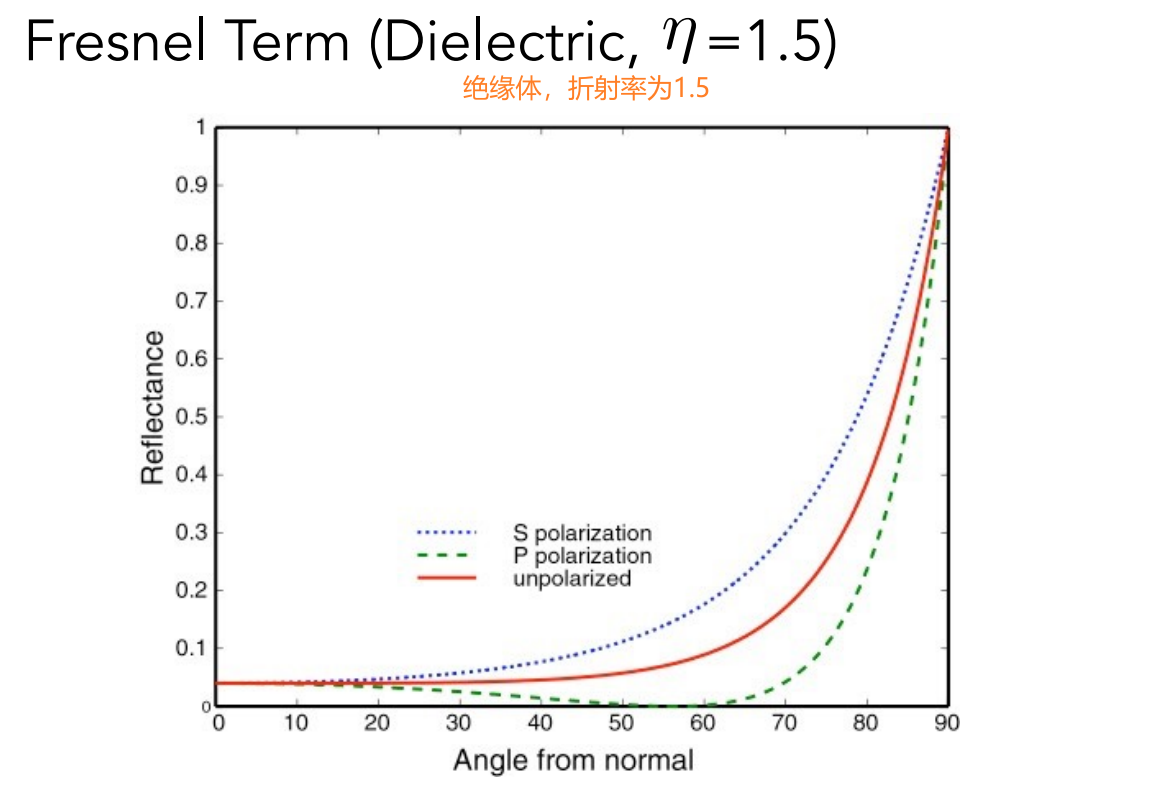
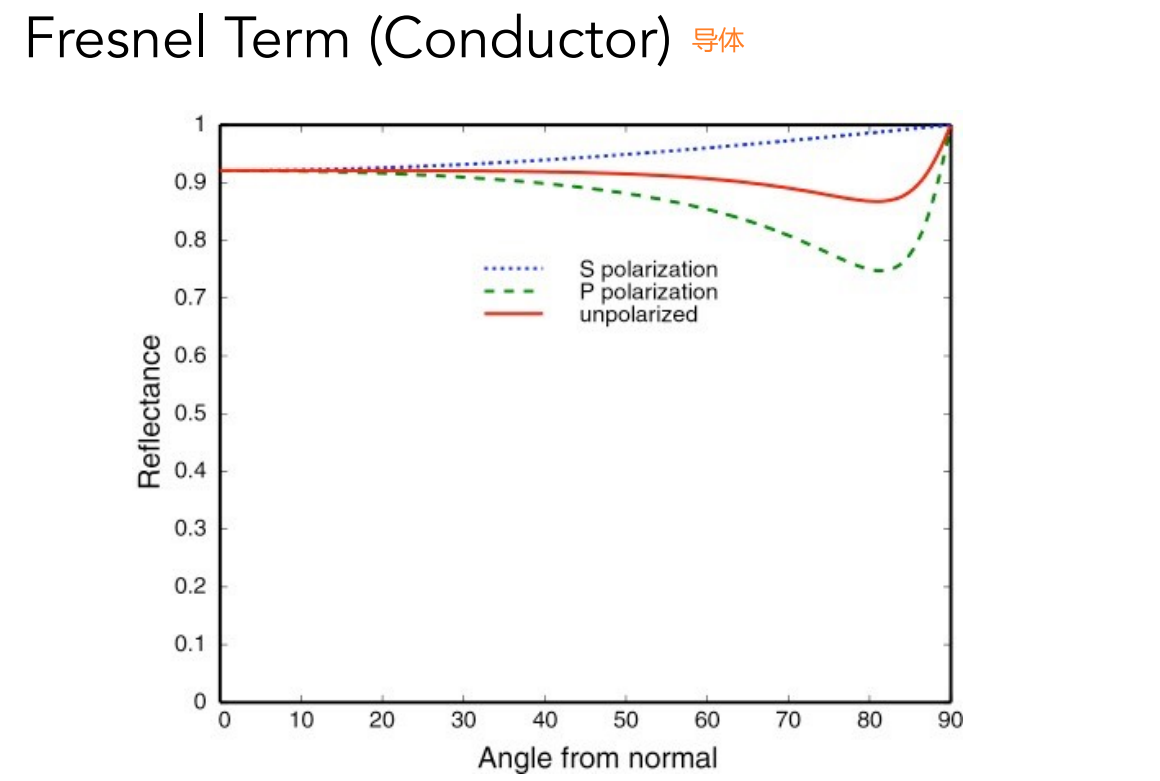
17.1.4 菲涅尔项:多少光反射,多少光折射
- 反射率取决于入射角度

17.2 微表面模型 Microfacet Material
- 从近处看:看到几何
- 从远处看:看到材质、外观

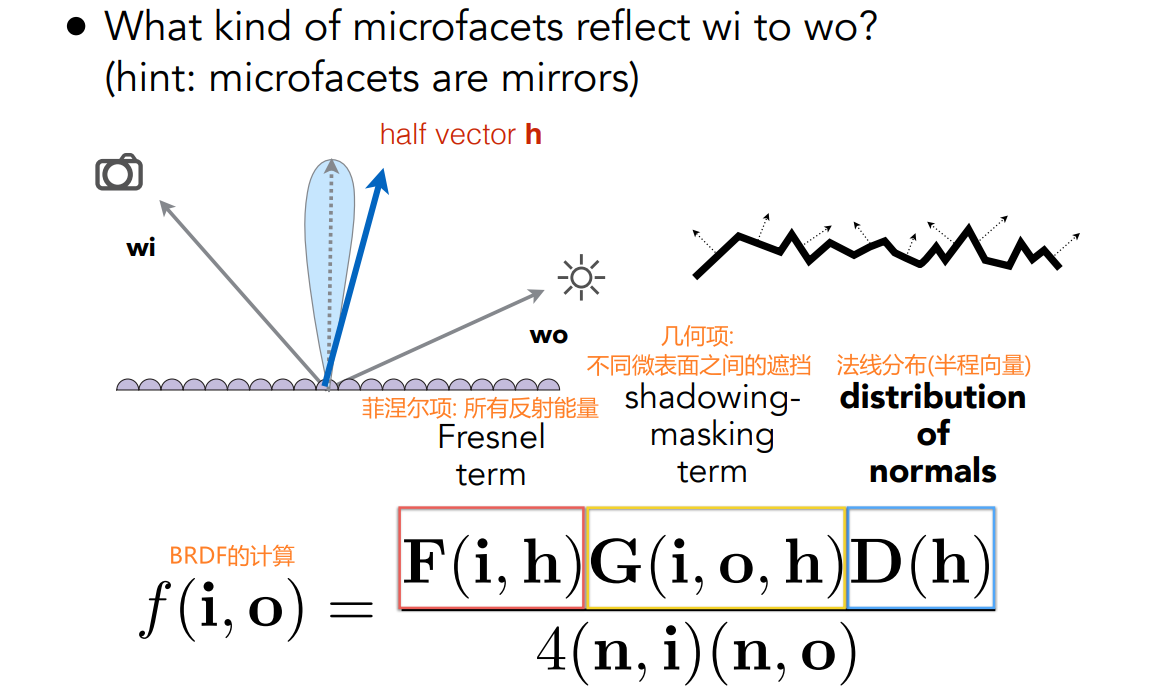
17.2.1 微表面BRDF
- 微表面都是完全的镜子,只有在镜面反射方向,才能看到反射光线
- 微表面的法线分布,可以表示表面的粗糙程度
- 法线分布集中 <=> glossy
- 法线分布发散 <=> diffuse
- 当光线接近平行射入表面时,微表面之间的相互遮挡较大
- 称为grazing angle

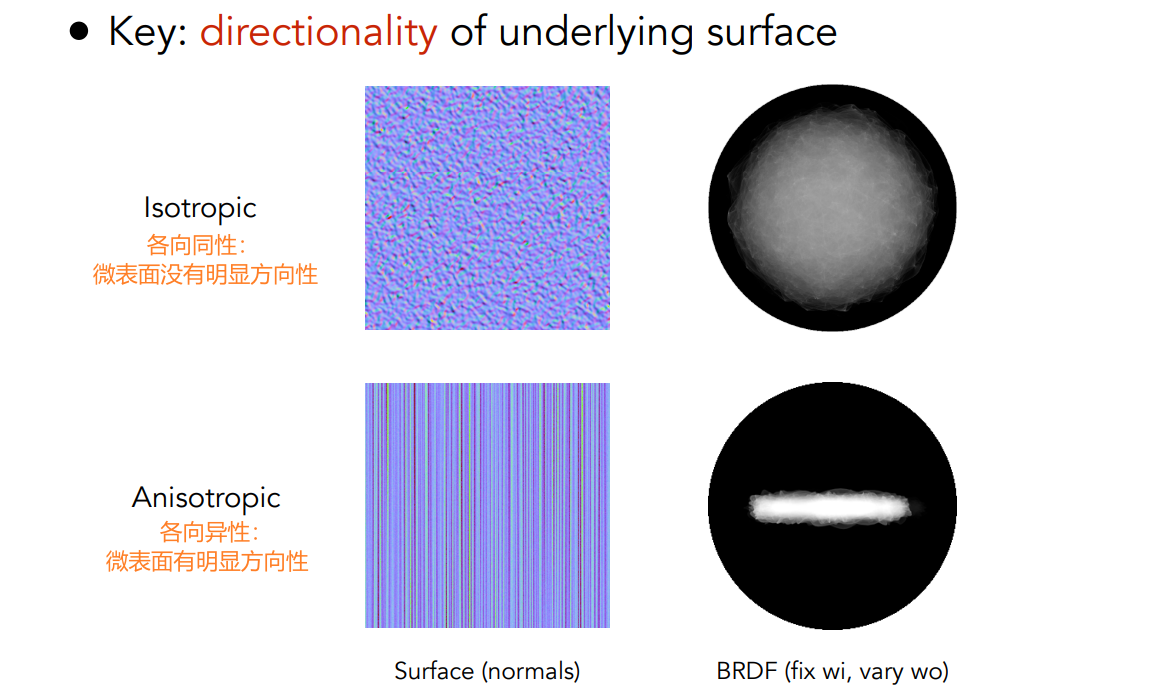
17.2.2 各向同性/各向异性材质 Isotropic/Anisotropic Materials

17.3 BRDF的性质
值非负:\(f_r(\omega_i \rightarrow \omega_r) \ge 0\)
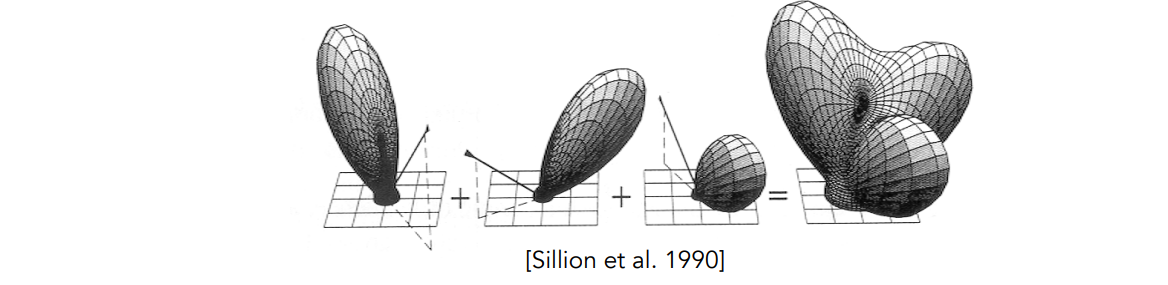
线性性质:\(L_r(p,\omega_r)=\int_{H^2}f_r(p,\omega_i \rightarrow \omega_r)L_i(p, \omega_i)cos \theta_i\ d\omega_i\)
- 可以分成很多块,然后相加
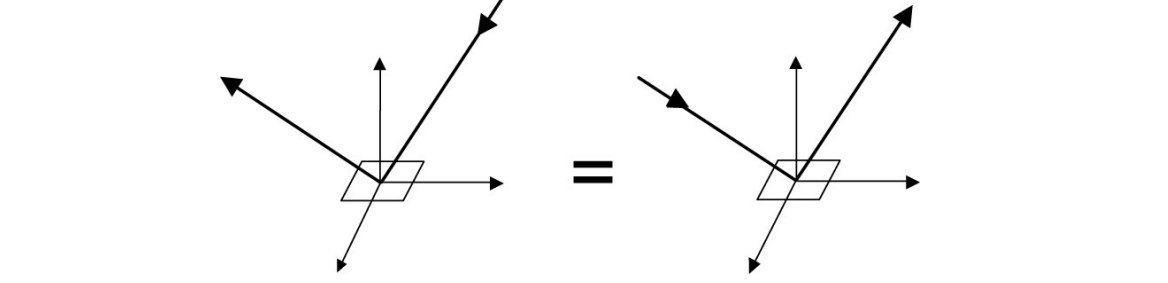
可逆性:\(f_r(\omega_i \rightarrow \omega_r) = f_r(\omega_r \rightarrow \omega_i)\)
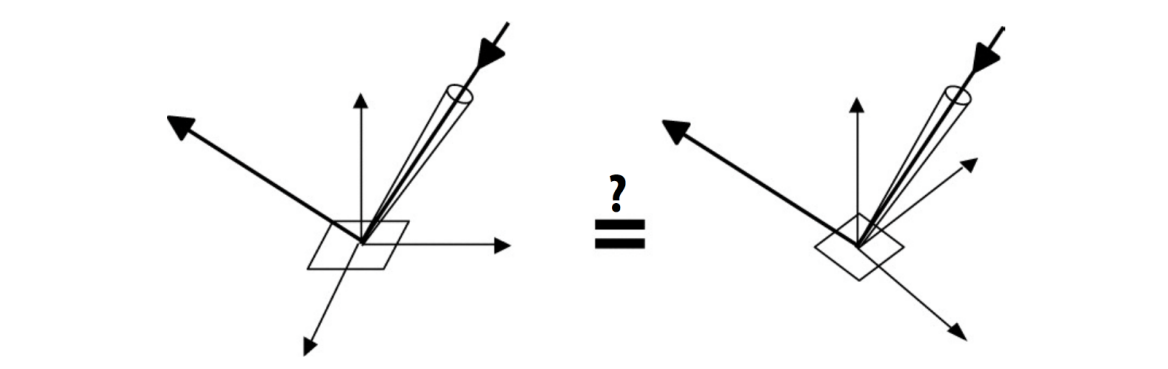
能量守恒:\(\forall \omega_r, \int_{H^2}f_r(\omega_i \rightarrow \omega_r)cos \theta_i\ d\omega_i \le 1\)
- BRDF不可能让能量变多
- 因此,光线追踪经过很多次反射后,能量会收敛
各向同性 & 各向异性
- 各向同性:\(f_r(\theta_i,\phi_i;\theta_r,\phi_r)=f_r(\theta_i,\theta_r,\phi_r-\phi_i)\)
- 降低了一个维度的自由度
- 考虑对称性,对于所有的BRDF:\(f_r(\theta_i,\theta_r,\phi_r-\phi_i)=f_r(\theta_r,\theta_i,\phi_i-\phi_r)=f_r(\theta_i,\theta_r,|\phi_r-\phi_i|)\)
- 各向同性:\(f_r(\theta_i,\phi_i;\theta_r,\phi_r)=f_r(\theta_i,\theta_r,\phi_r-\phi_i)\)
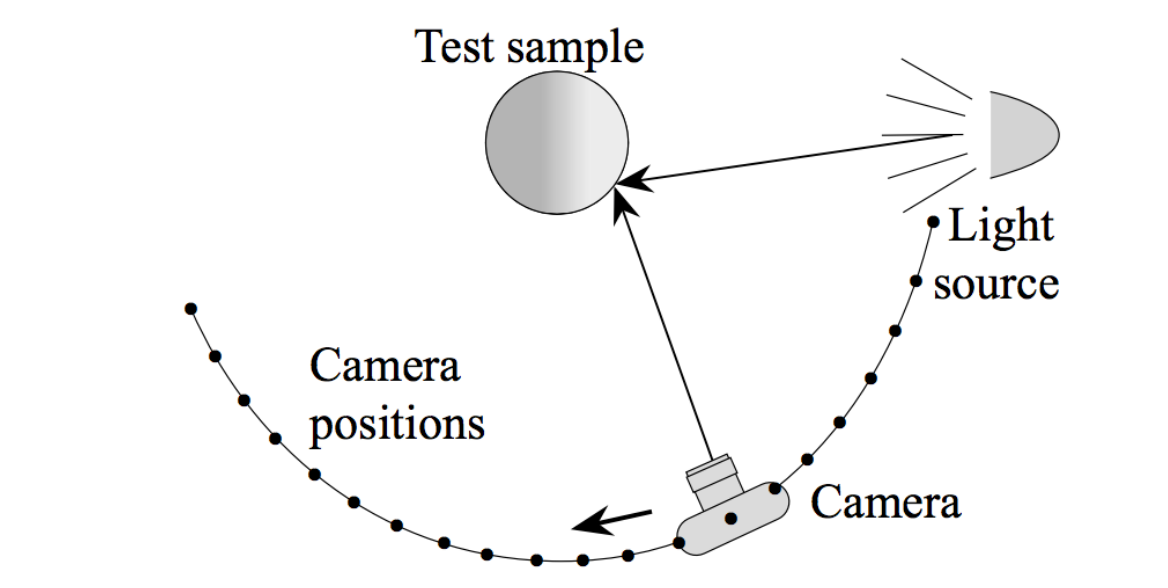
17.4 测量BRDF
- 给定一个光源(入射方向)、一个摄像机(出射方向)
- 更改这光源和摄像机的位置,测量对应的BRDF
- 优化:
- 对于各向同性的物体,可以通过方位角,将4D转化为3D
- 可逆性:降低了一半的测量次数
17.5 保存BRDF
MERL BRDF Database:
- 测量了很多不同的材质
- 保存为三维数组

本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 华风夏韵!
评论