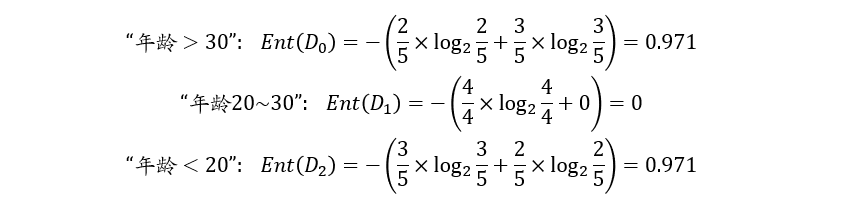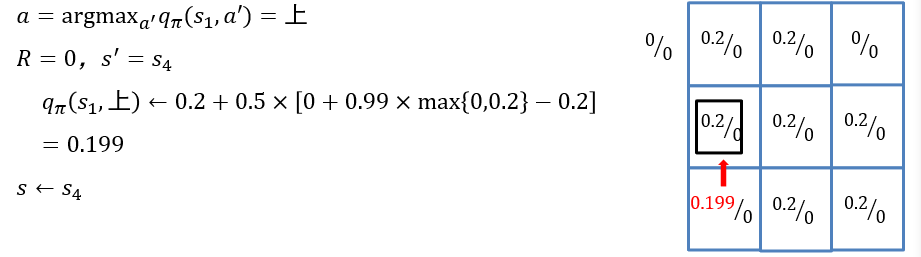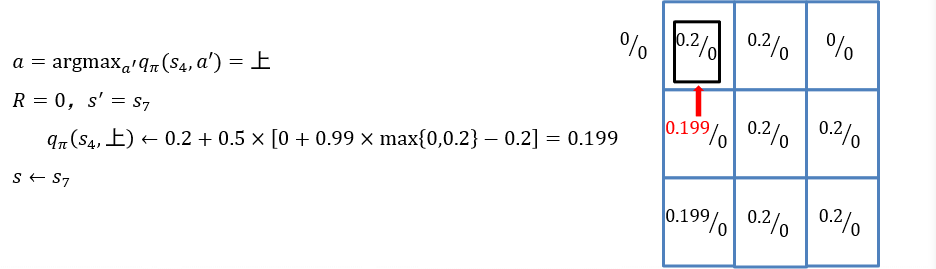人工智能
一、逻辑与推理
- 符号主义人工智能中,所有概念均可通过人类可理解的“符号”及符号之间的关系来表示
- 符号主义人工智能方法基于如下假设:
- 可通过逻辑方法来对符号及其关系进行计算,实现逻辑推理,辨析符号所描述内容是否正确
1.1 命题逻辑 proposition logic
1.1.1 定义
命题逻辑:是应用一套形式化规则对以符号表示的描述性陈述进行推理的系统
原子命题:一个或真或假的描述性陈述被称为原子命题
- 对原子命题的内部结构不做任何解析
复合命题(compound proposition):若干原子命题可通过逻辑运算符来构成复合命题
命题联结词(connectives):通过命题联结词对已有命题进行组合,得到新命题
- 通过命题联结词得到的命题被称为复合命题
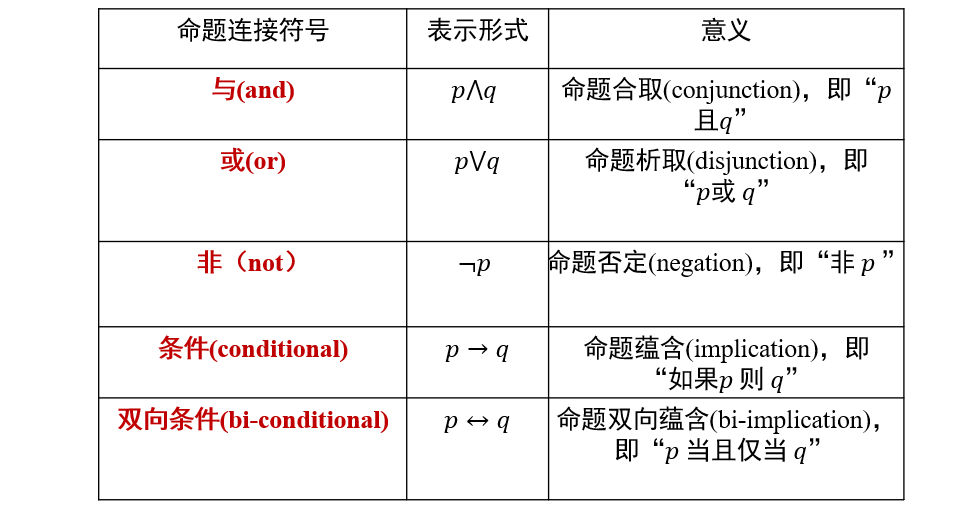
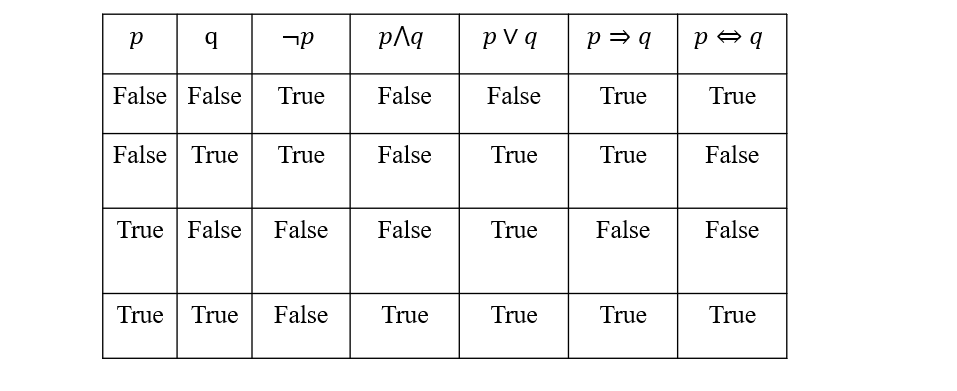
通过真值表来计算复合命题的真假
- p=>q是一个蕴含关系,表示p∈q
- 如果p=False,则p=>q恒为True
1.1.2 逻辑等价
- 逻辑等价:给定命题p和命题q,如果p和q在所有情况下都具有同样真假结果,那么p和q在逻辑上等价,即p≡q

1.1.3 推理规则
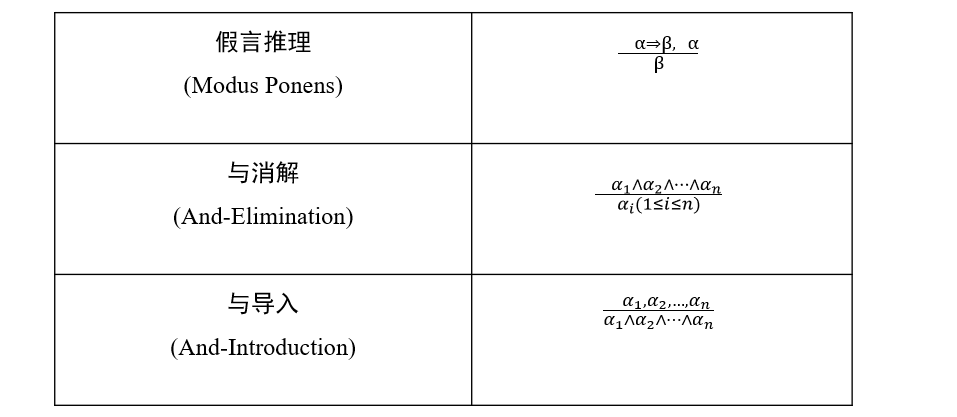

示例:
1.1.4 命题范式
范式(normal form):把命题公式化归为一种标准的形式
范式最大的作用是可以进行两个命题的等价判定
析取范式:有限个简单合取式构成的析取式
合取范式:有限个简单析取式构成的合取式

一个析取范式是不成立的,当且仅当:它的每个简单合取式都不成立
一个合取范式是成立的,当且仅当:它的每个简单析取式都是成立的
任一命题公式都存在着与之等值的析取范式与合取范式
- 注意:命题公式的析取范式与合取范式都不是唯一的

1.2 谓词逻辑
1.2.1 个体与谓词
个体:个体是指所研究领域中可以独立存在的具体或抽象的概念
谓词:谓词是用来刻画个体属性或者描述个体之间关系存在性的元素,其值为真或为假
- 包含一个参数的谓词称为一元谓词,表示一元关系
- 包含多个参数的谓词称为多元谓词,表示个体之间的多元关系

函数与谓词的区别:

1.2.2 量词
- 全称量词(universal quantifier, ∀):∀xP(x)表示定义域中的所有个体具有性质P
- 存在量词(existential quantifier, ∃):∃xP(x)表示定义域中存在一个个体或若干个体具有性质P

1.2.3 变元
约束变元:在全称量词或存在量词的约束条件下的变量符号称为约束变元
自由变元:不受全称量词或存在量词约束的变量符号称为自由变元

在约束变元相同的情况下,量词的运算满足分配律

当公式中存在多个量词时,若多个量词都是全称量词或者都是存在量词,则量词的位置可以互换;若多个量词中既有全称量词又有存在量词,则量词的位置不可以随意互换

1.2.4 项与原子谓词公式
- 项:项是描述对象的逻辑表达式,被递归地定义为:
- 常量符号和变量符号是项;
- 若\(f(x_1,x_2,⋯,x_n)\)是\(n\)元函数符号,\(t_1,t_2,⋯,t_n\)是项,则\(f(t_1,t_2,⋯,t_n)\)是项;
- 有限次数地使用上述规则产生的符号串是项。
- 原子谓词公式:
- 若\(P(x_1,x_2,⋯,x_n)\)是\(n\)元谓词,\(t_1,t_2,⋯,t_n\)是项,则称\(P(t_1,t_2,⋯,t_n)\)是原子谓词公式,简称原子公式
1.2.5 合式公式
合式公式是由逻辑联结词和原子公式构成的用于陈述事实的复杂语句,又称谓词公式,由以下规则定义:
- 命题常项、命题变项、原子谓词公式是合式公式
- 如果A是合式公式,则¬A也是合式公式
- 如果A和B是合式公式,则A∧B、A∨B、A→B 、B→A、A⟷B 都是合式公式
- 如果A是合式公式,x是个体变项,则(∃x)A(x) 和(∀x)A(x)也是合式公式
- 有限次数地使用上述规则构成的表达式是合式公式
1.2.6 推理规则

1.2.7 专家系统的构成
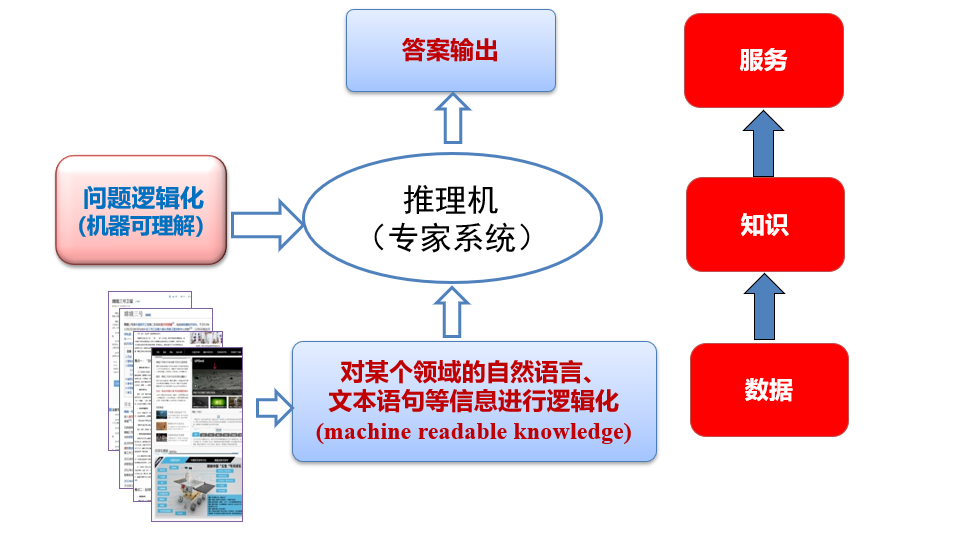
1.3 知识图谱
1.3.1 基本概念
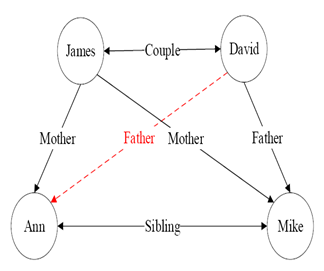
- 知识图谱可视为包含多种关系的图
- 在图中,每个节点是一个实体(如人名、地名、事件和活动等)
- 任意两个节点之间的边表示这两个节点之间存在的关系
- 一般而言,可将知识图谱中任意两个相连节点及其连接边表示成一个三元组(triplet), 即 (left_node, relation, right_node)
- 知识图谱中存在连线的两个实体可表达为形如<left_node,
relation, right_node >的三元组形式
- 这种三元组也可以表示为一阶逻辑(first order logic, FOL)的形式,从而为基于知识图谱的推理创造了条件
- 例如从<奥巴马,出生地,夏威夷>和<夏威夷,属于,美国>两个三元组,可推理得到<奥巴马,国籍,美国>
1.3.2 知识图谱推理
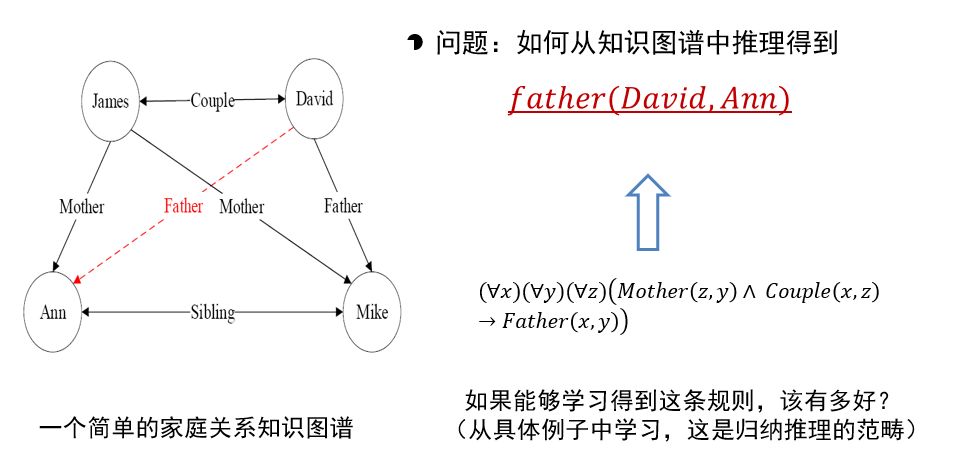
- 可利用一阶谓词来表达刻画知识图谱中节点之间存在的关系
- 如图中形如<James,Couple,David>的关系可用一阶逻辑的形式来描述,即Couple(James, David)
- Couple(x, y)是一阶谓词,Couple是图中实体之间具有的关系,x和y是谓词变量
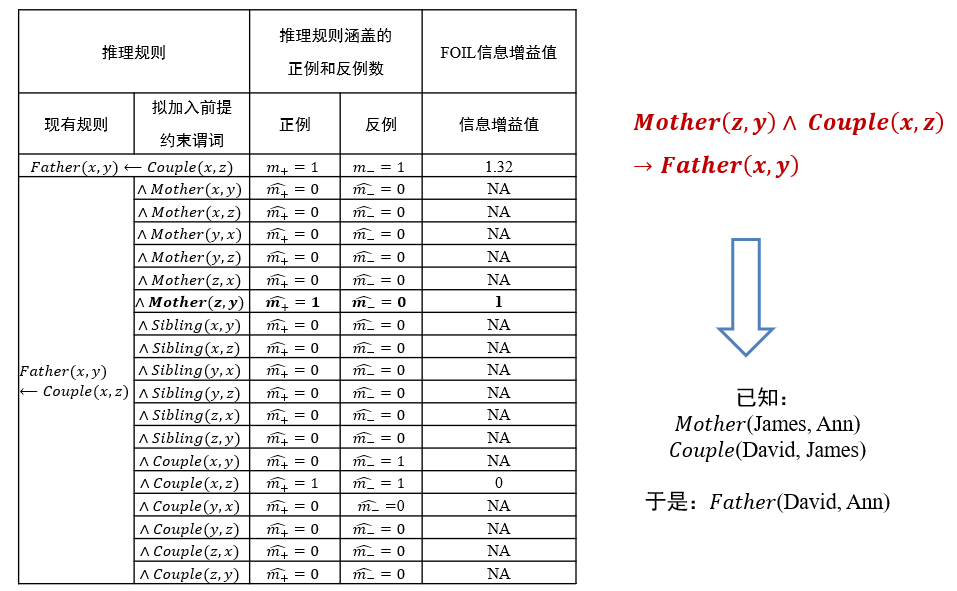
- 从图中已有关系可推知David和Ann具有父女关系,但这一关系在图中初始图(无红线)中并不存在,是需要推理的目标
1.3.3 归纳学习
- 归纳逻辑程序设计ILP(Inductive Logic Programming):是机器学习和逻辑程序设计交叉领域的研究内容
- ILP使用一阶谓词逻辑进行知识表示,通过修改和扩充逻辑表达式对现有知识归纳,完成推理任务
- 作为ILP的代表性方法,FOIL(First Order Inductive Learner)通过序贯覆盖实现规则推理
1.3.4 一阶推导学习 FOIL
FOIL:First Order Inductive Learner

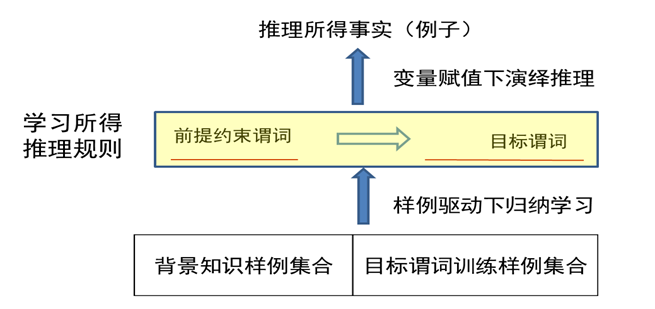
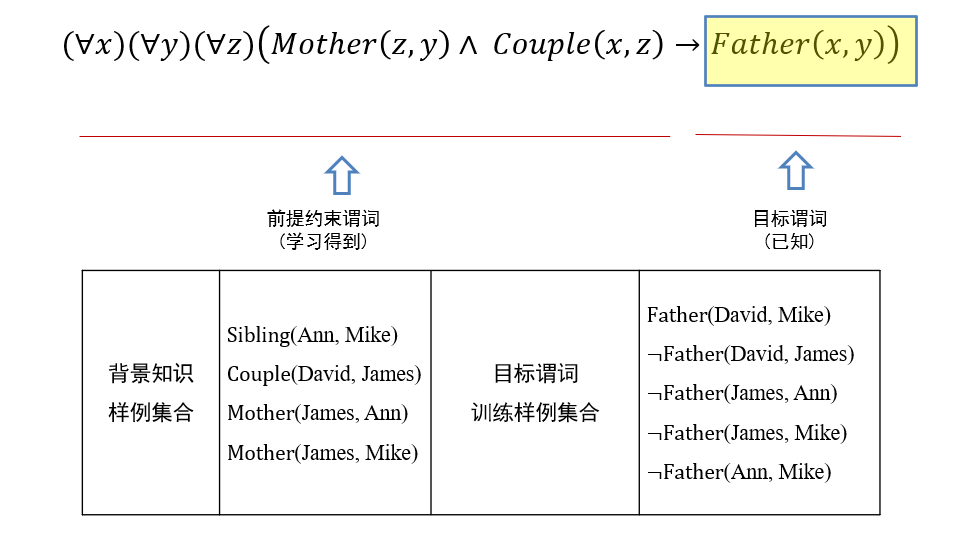
目标谓词:
Father(x, y)正例:目标谓词只有一个正例
Father(David, Mike)。反例:在知识图谱中一般不会显式给出,但可从知识图谱中构造出来
- 如从知识图谱中已经知道
Couple(David, James)成立,则Father(David, James)可作为目标谓词P的一个反例,记为¬Father (David, James)。 - 只能在已知两个实体的关系且确定其关系与目标谓词相悖时,才能将这两个实体用于构建目标谓词的反例
- 而不能在不知两个实体是否满足目标谓词前提下将它们来构造目标谓词的反例
- 如从知识图谱中已经知道
背景知识:知识图谱中目标谓词以外的其他谓词实例化结果,如
Sibling(Ann, Mike)推理思路:从一般到特殊,逐步给目标谓词添加前提约束谓词,直到所构成的推理规则不覆盖任何反例
- 从一般到特殊:对目标谓词或前提约束谓词中的变量赋予具体值
- 如将
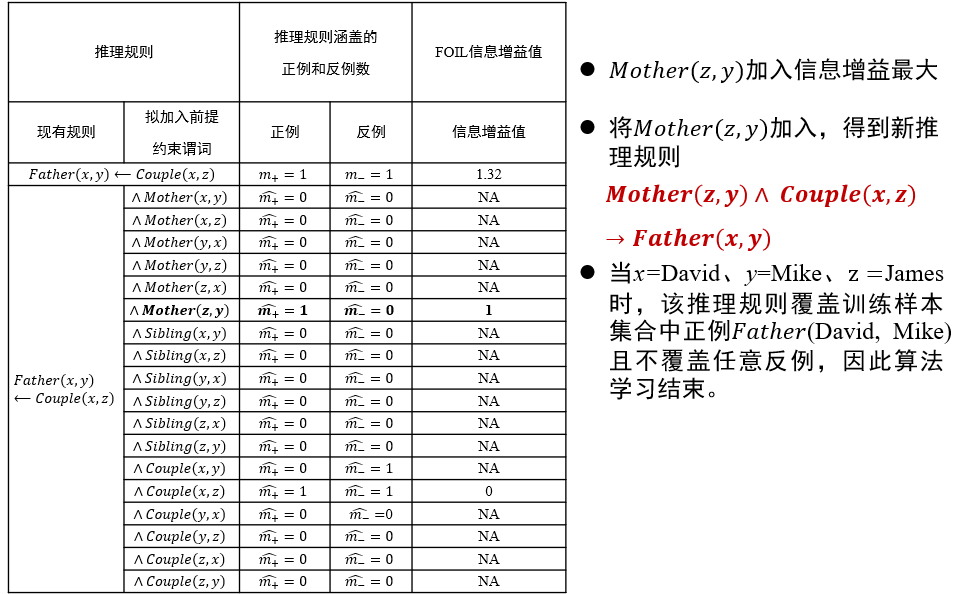
(∀x)(∀y)(∀z)(Mother(z, y)∧Couple(x,z) → Father(x, y))这一推理规则所包含的目标谓词Father(x, y)中x和y分别赋值为David和Ann,进而进行推理
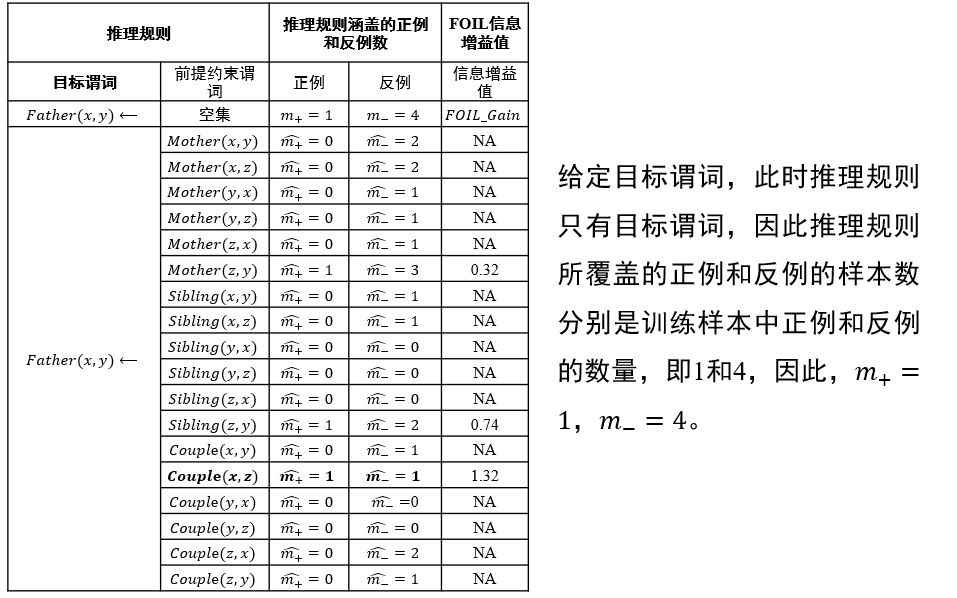
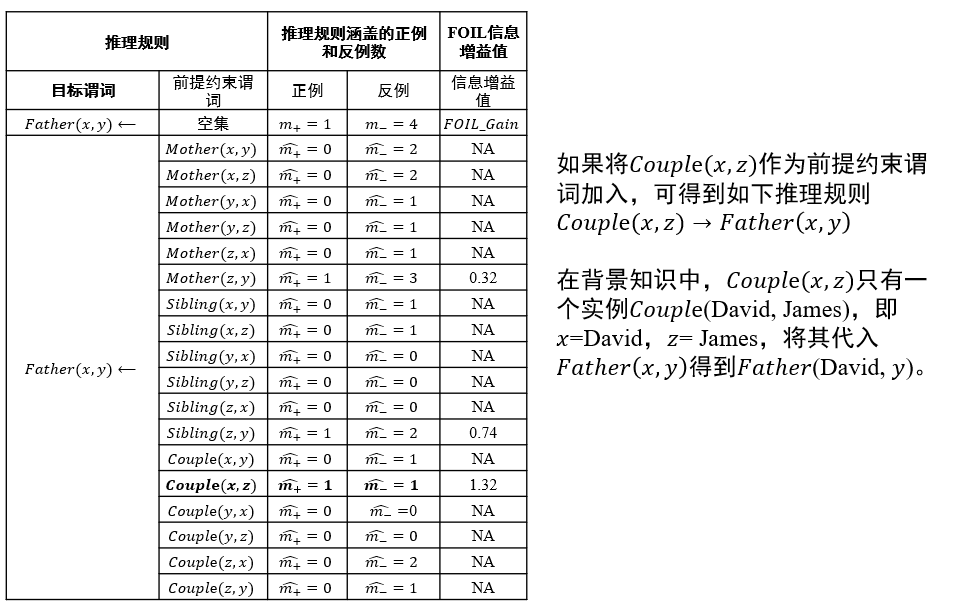
如何选择约束谓词:信息增益值最大
- 要求添加该谓词后,可以覆盖的正例更多,负例更少
- 直到只覆盖正例,不覆盖负例
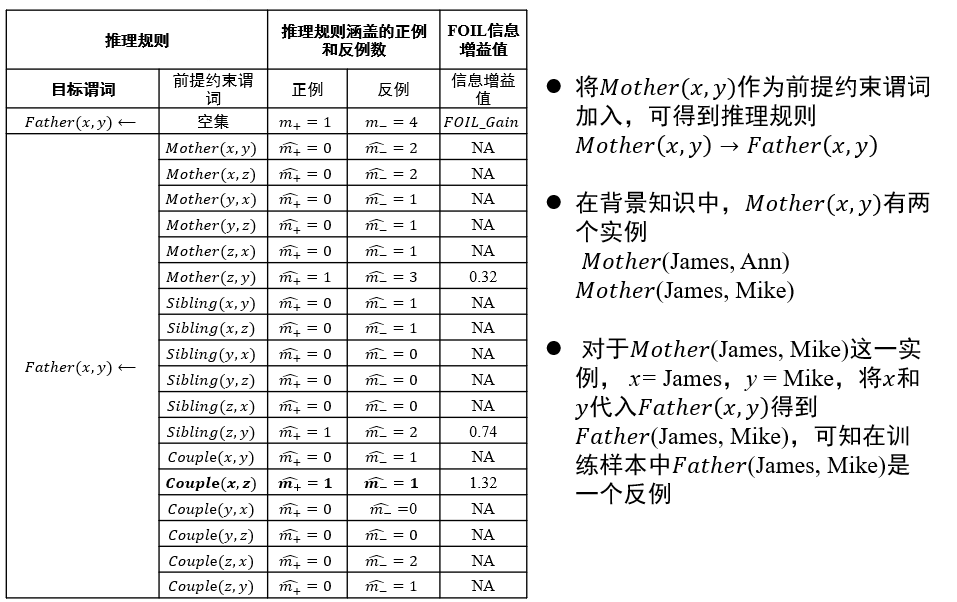
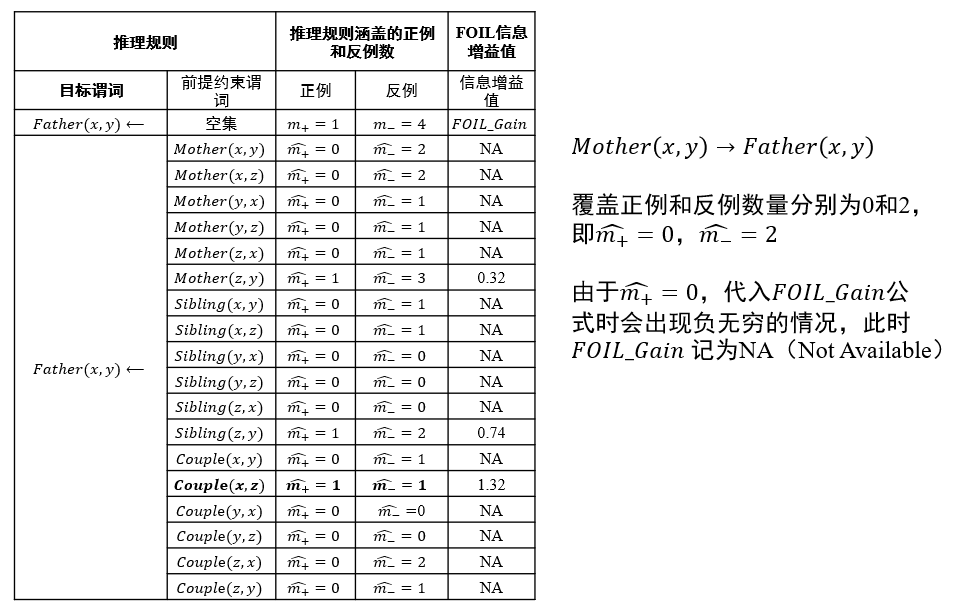
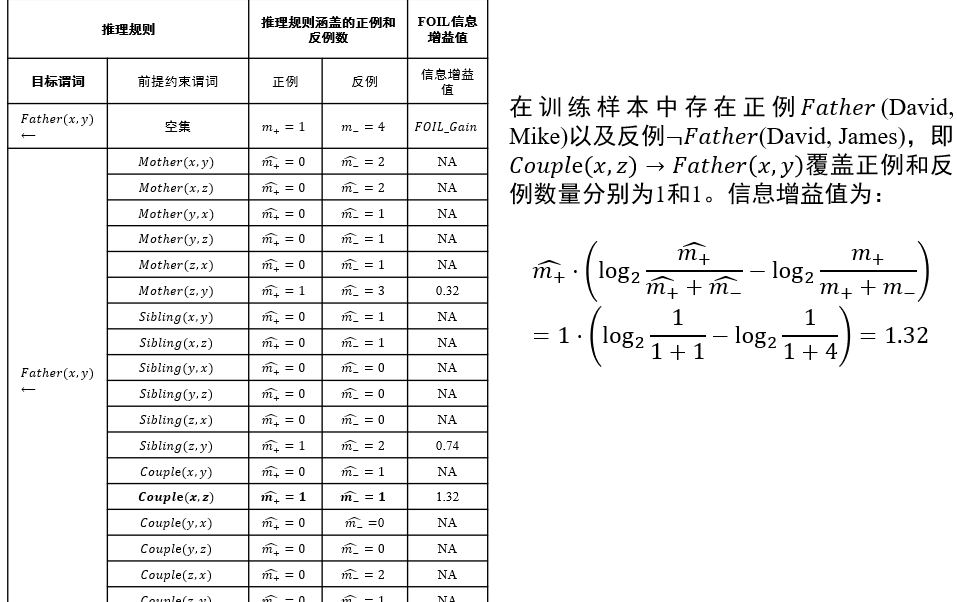
信息增益值:描述了添加某个谓词后,\(\frac{正例}{正例+反例}\)的比例变化 \[ FOIL\_Gain=\hat{m_+}(\log_2\frac{\hat{m_+}}{\hat{m_+}+\hat{m_-}}-\log_2\frac{m_+}{m_++m_-}) \]

示例:
1.3.5 路径排序推理 PRA
Path Ranking Algorithm
- 基本思想:将实体之间的关联路径作为特征,来学习目标关系的分类器
- 工作流程主要分为三步:
- 特征抽取:生成并选择路径特征集合
- 生成路径的方式有:随机游走、广度优先搜索、深度优先搜索等
- 特征计算:计算每个训练样例的特征值\(𝑃(𝑠→𝑡;𝜋_𝑗)\)
- 该特征值可以是:从实体节点\(𝑠\)出发,通过关系路径\(𝜋_𝑗\)到达实体节点\(𝑡\)的概率;
- 也可以是:布尔值,表示实体\(𝑠\)到实体\(𝑡\)之间是否存在路径\(𝜋_𝑗\);
- 还可以是:实体\(𝑠\)和实体\(𝑡\)之间路径出现频次、频率等
- 分类器训练:根据训练样例的特征值,为目标关系训练分类器
- 当训练好分类器后,即可将该分类器用于推理两个实体之间是否存在目标关系
- 特征抽取:生成并选择路径特征集合
特征向量的含义:布尔值,表示实体\(𝑠\)到实体\(𝑡\)之间是否存在路径\(𝜋_𝑗\);
- [Couple→Mother,Father→Mother-1,Mother→Sibling,Couple→Father]
如(David, Ann):只可以通过Couple→Mother这条路径链接,因此特征向量是[1, 0, 0, 0]

1.3.6 基于分布式的知识推理

1.3.7 马尔可夫逻辑网络

(不考)1.4 因果推理
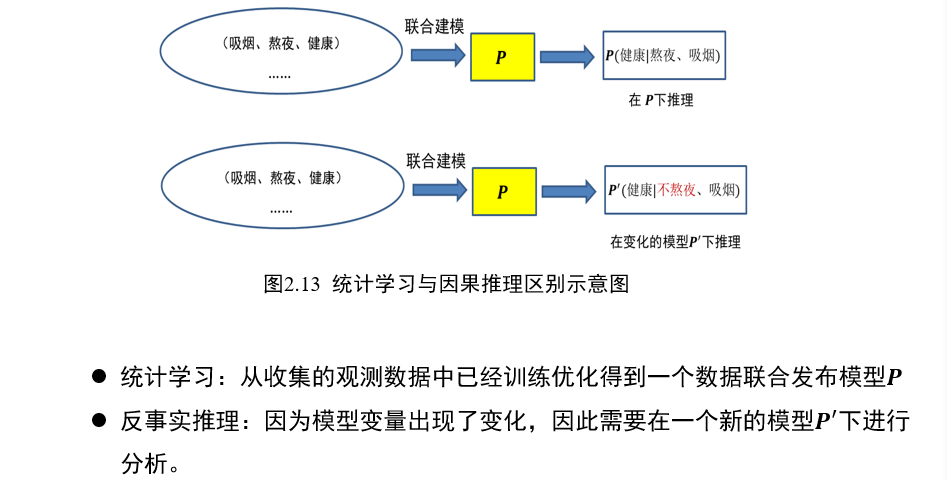
传统以统计建模为核心的推理手段:AI学习联合分布的概率
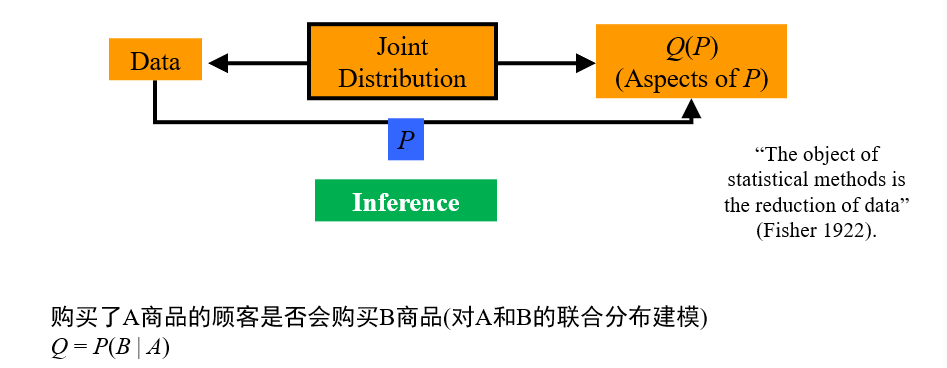
因果推理:改变控制变量的取值后,会导致结果如何变化
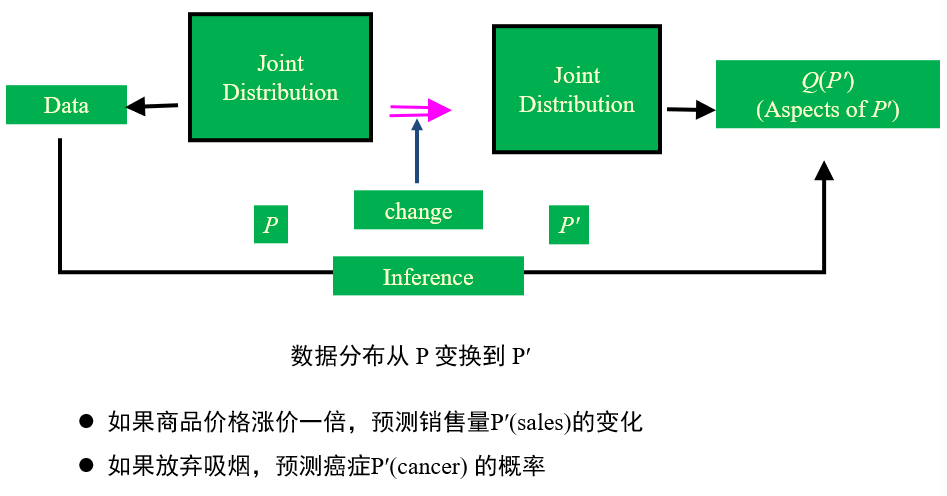
(不考)1.4.1 三种因果推理

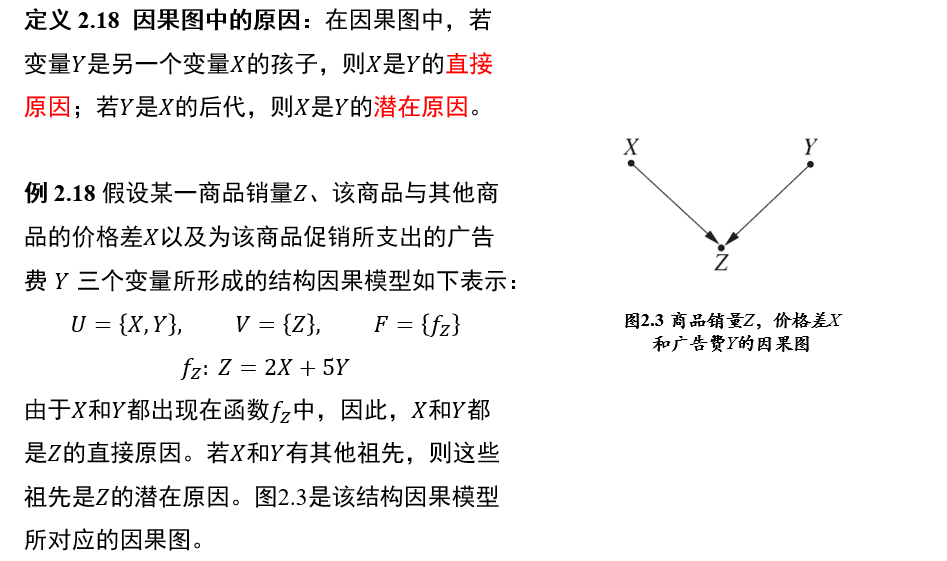
(不考)1.4.2 因果推理的主要模型

(不考)1.4.3 结构因果模型


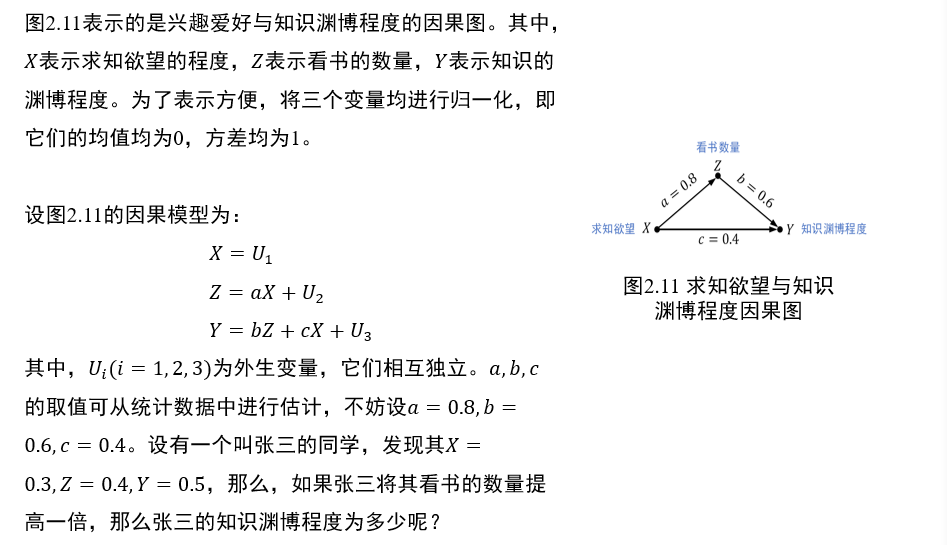
(不考)1.5 因果图模型
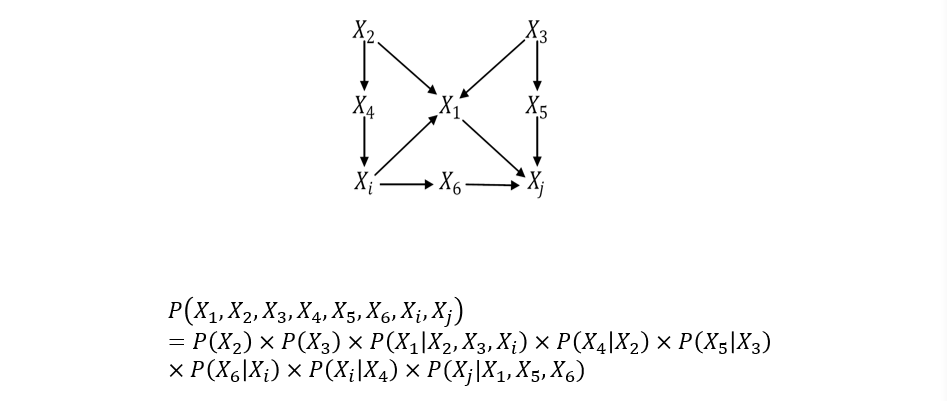
(不考)1.5.1 联合概率分布

(不考)1.5.2 链
中间节点\(Z\)一旦给定,两端的节点\(X,Y\)条件独立

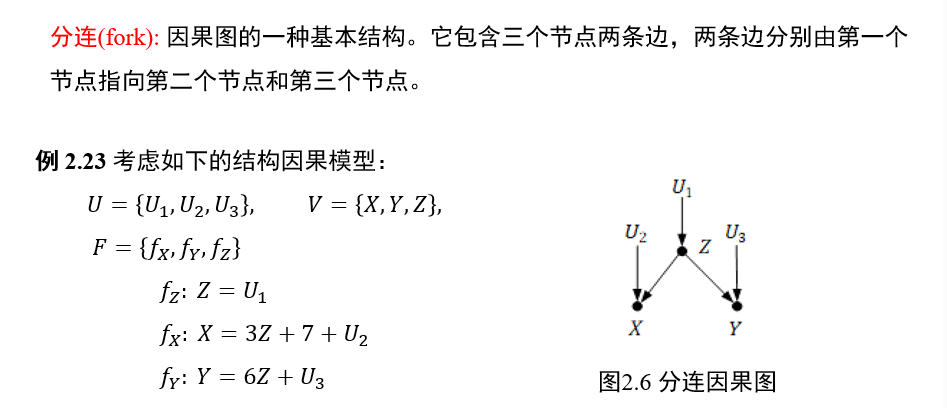
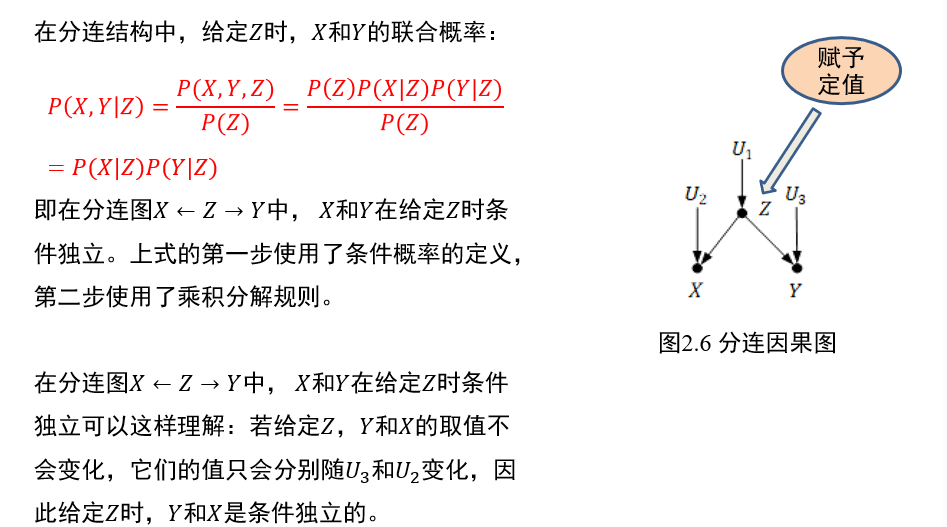
(不考)1.5.3 分连
中间节点\(Z\)一旦给定,两端的节点\(X,Y\)条件独立
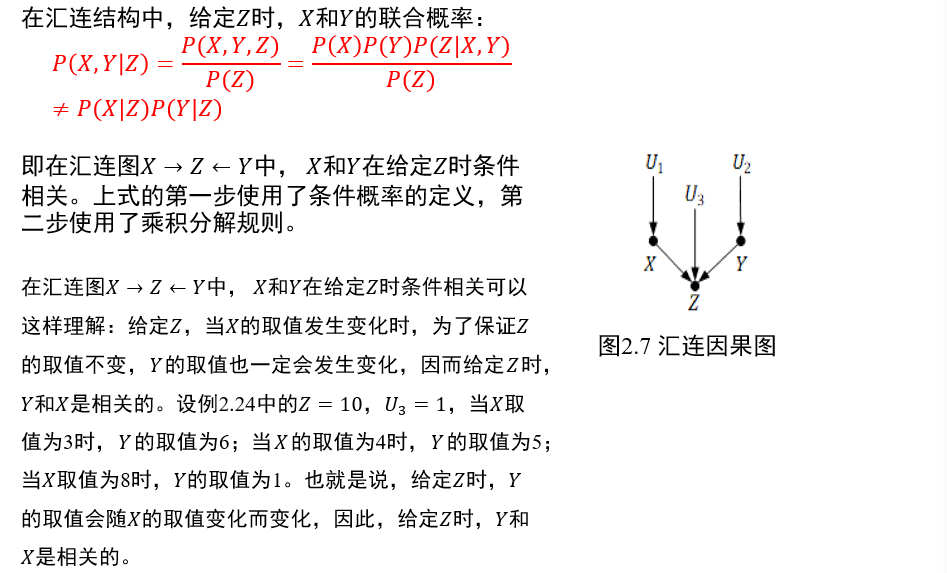
(不考)1.5.4 汇连
中间节点\(Z\)给定时,两端的节点\(X,Y\)条件相关

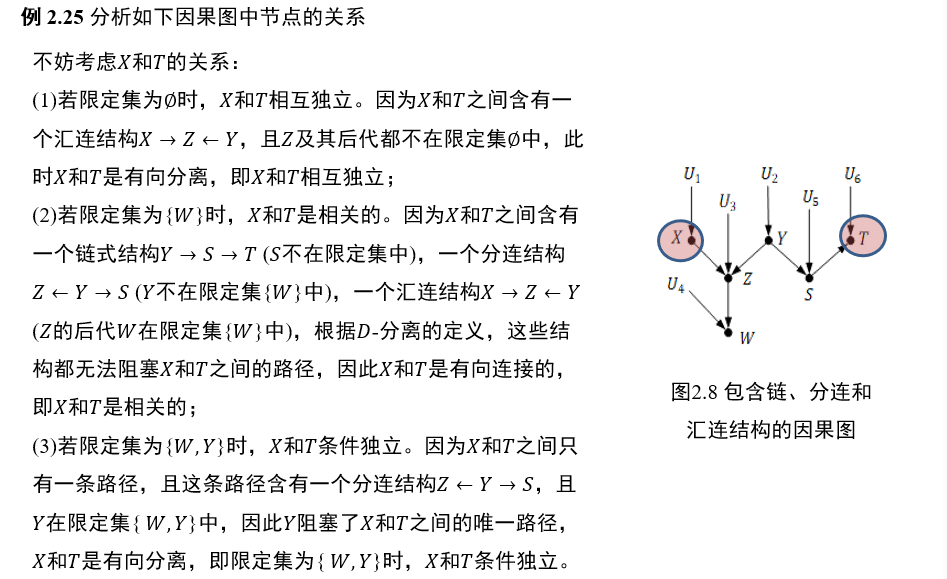
(不考)1.5.5 D-分离

(不考)1.5.6 干预的因果效应

(不考)1.5.7 因果效应差
因果效应差越大,表示该变量对结果的因果效应越大


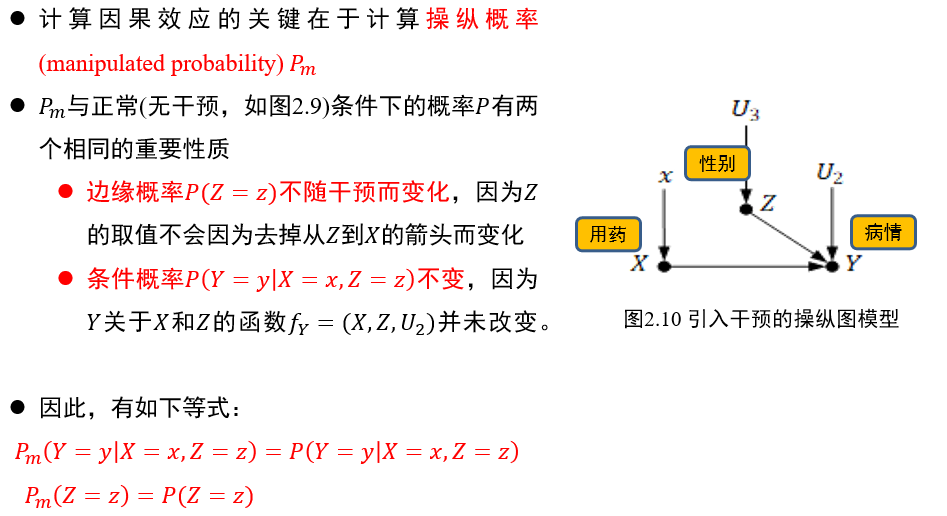



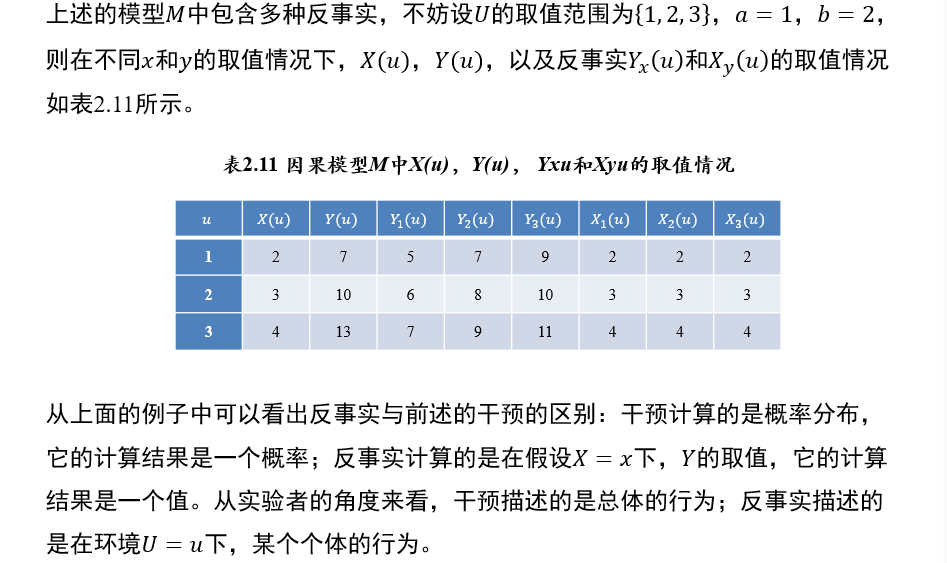
(不考)1.5.8 反事实模型



二、搜索与求解
2.1 搜索算法基础
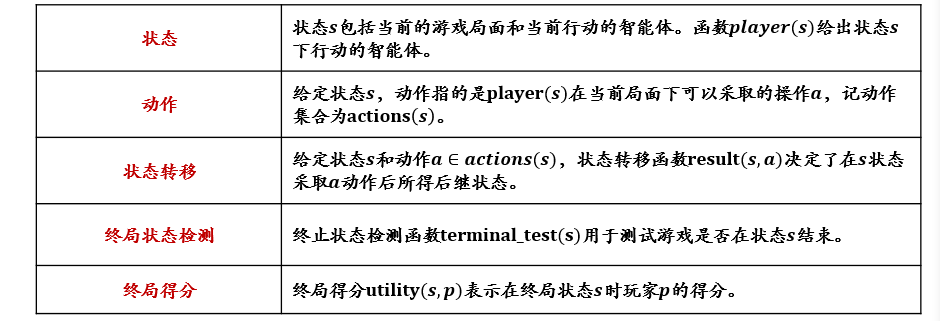
2.1.1 搜索算法的形式化描述
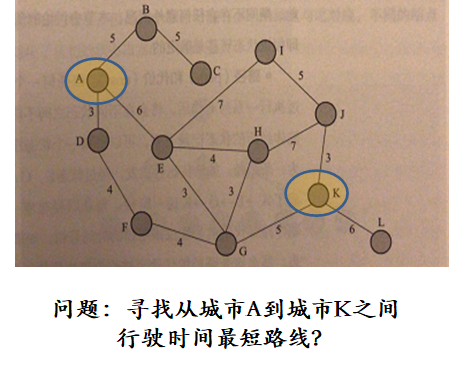
- 状态:对智能体和环境当前情形的描述
- 例如,在最短路径问题中,城市可作为状态
- 将原问题城市对应的状态称为初始状态
- 动作:从当前时刻所处状态转移到下一时刻所处状态所进行操作
- 一般而言这些操作都是离散的
- 状态转移:智能体选择了一个动作之后,其所处状态的相应变化
- 路径/代价:一个状态序列。该状态序列被一系列操作所连接
- 如从A到K所形成的路径。
- 目标测试:评估当前状态是否为所求解的目标状态
2.1.2 评价指标
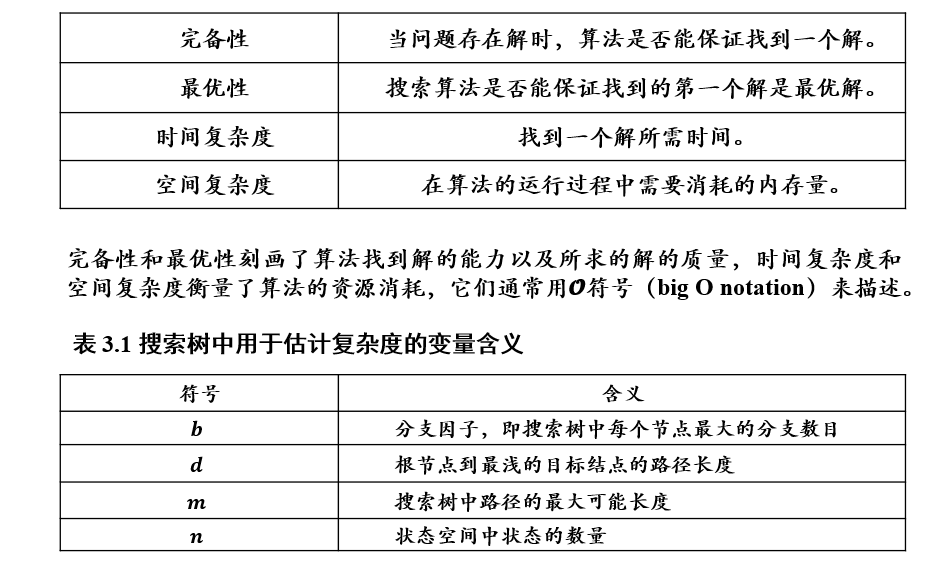
2.1.3 树搜索

2.1.4 剪枝搜索
主动放弃一些后继节点,可以提高搜索效率,而不会影响最终的搜索效果
- 如删除已访问节点

2.2 启发式搜索
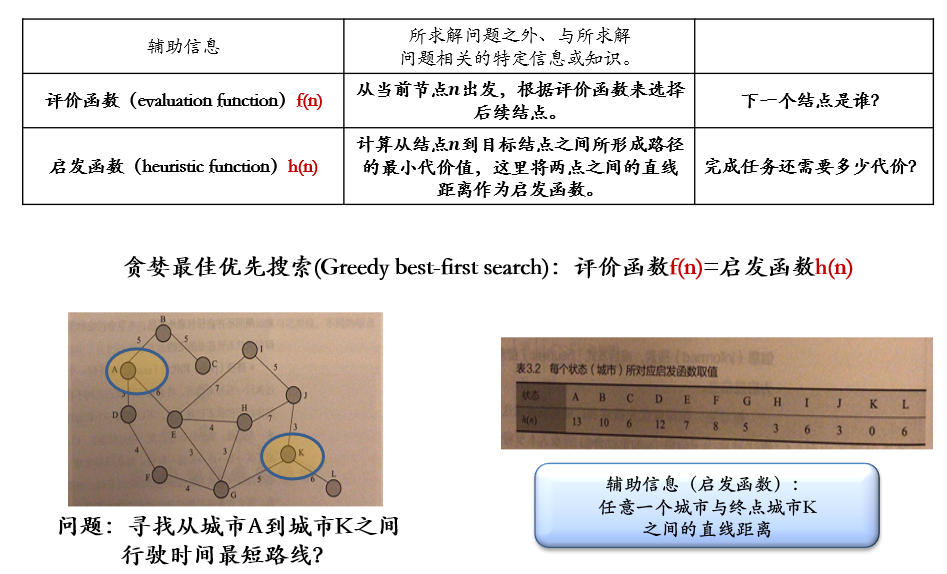
2.2.1 贪婪最佳优先搜索 Greedy best-first search
评价函数f(n) =
启发函数h(n)
f(n):评价函数,判定下一个节点是谁h(n):启发函数,预估完成任务的最小代价
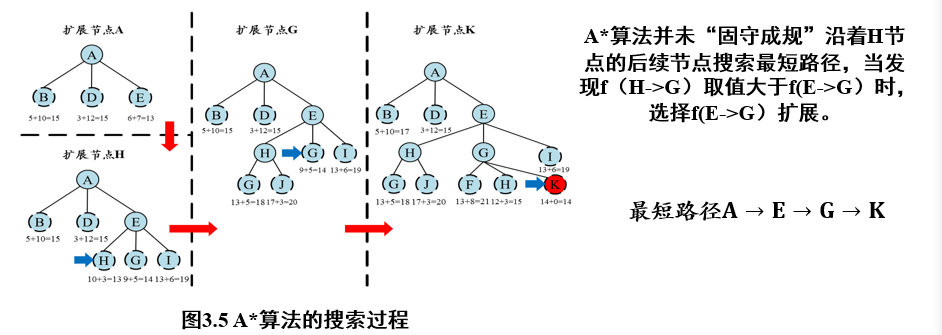
2.2.2 A*算法
2.2.2.1 A*算法的定义
评价函数f(n) = g(n) + h(n)
f(n):评价函数,判定下一个节点是谁h(n):启发函数,预估完成任务的最小代价g(n):从起始节点到当前节点的代价

(不考)2.2.2.2 A*算法的性能分析
A*算法的完备性、最优性,取决于搜索问题和启发函数的性质
- 完备性:一定能找到解
- 最优性:解最优
相关定义
f(n):评价函数,判定下一个节点是谁h(n):启发函数,预估完成任务的最小代价g(n):从起始节点到当前节点的代价c(n,a,n'):从节点n,执行动作a,到达节点n'的单步代价h*(n):从节点n到终点的实际最小代价
启发函数
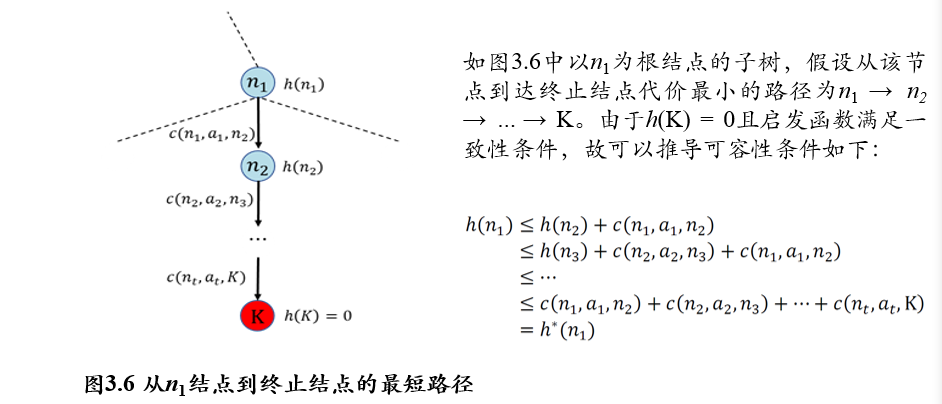
h(n)需要满足的性质:可容性admissible:
h(n) ≤ h*(n),预估代价不超过实际代价一致性consistency:
h(n) ≤ c(n,a,n') + h(n'),从当前节点直接到达终点的代价,不超过到达下一节点,然后再到达终点的代价满足一致性,一定满足可容性:
(不考)2.2.2.3 A*算法的完备性
- 完备性:如果在起始节点和终止节点之间有路径存在,那么一定可以得到解。得不到解一定说明没有解存在

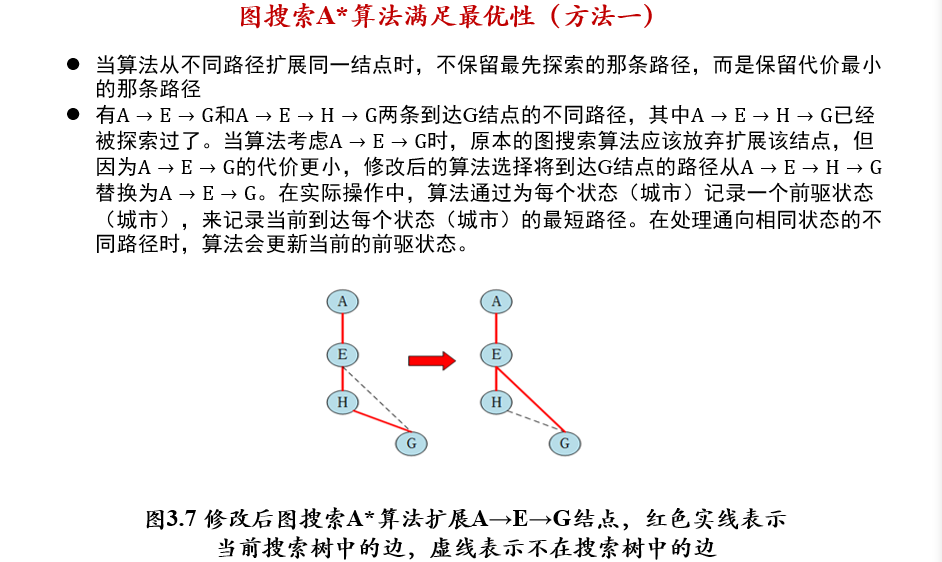
(不考)2.2.2.4 A*算法的最优性
- 树搜索算法:如果启发函数满足可容性,则A*算法满足最优性
- 图搜索算法:如果启发函数满足一致性,则A*算法满足最优性
- 对于任意一个状态t,它第一次被加入搜索树时的路径必然是最短路径


2.3 对抗搜索/博弈搜索
Adversarial / Game Search
在一个竞争的环境中,智能体(agents)之间通过竞争实现相反的利益,一方最大化这个利益,另外一方最小化这个利益
分为三种搜索策略
- 最小最大搜索(Minimax Search):最小最大搜索是在对抗搜索中最为基本的一种让玩家来计算最优策略的方法
- Alpha-Beta剪枝搜索(Pruning Search):一种对最小最大搜索进行改进的算法,即在搜索过程中可剪除无需搜索的分支节点,且不影响搜索结果。
- 蒙特卡洛树搜索(Monte-Carlo Tree Search):通过采样而非穷举方法来实现搜索
本书的讨论范围:
- 确定的、全局可观察的、竞争对手轮流行动、零和游戏
形式化描述:
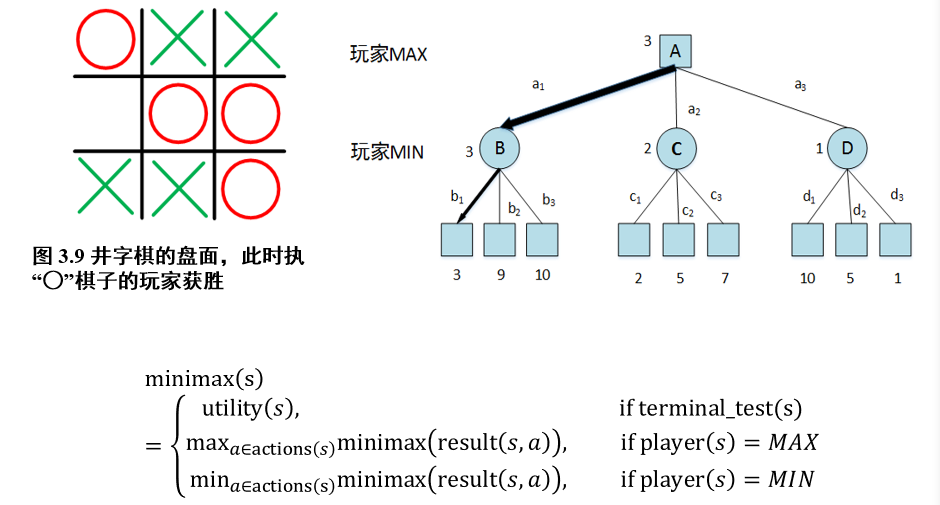
2.3.1 最小最大搜索 Minimax
- 当前收益:
minimax(s)- 选择动作
a后的可能收益:minimax(result(s,a))
- 如果为终止状态:返回当前状态的得分
utility(s) - 如果当前玩家为MAX:选择可能收益最大的动作,返回执行该动作后的可能收益
- 如果当前玩家为MIN:选择可能收益最小的动作,返回执行该动作后的可能收益

// 玩家MAX行动下, 当前的最优动作ans |
2.3.2 Alpha-Beta剪枝搜索
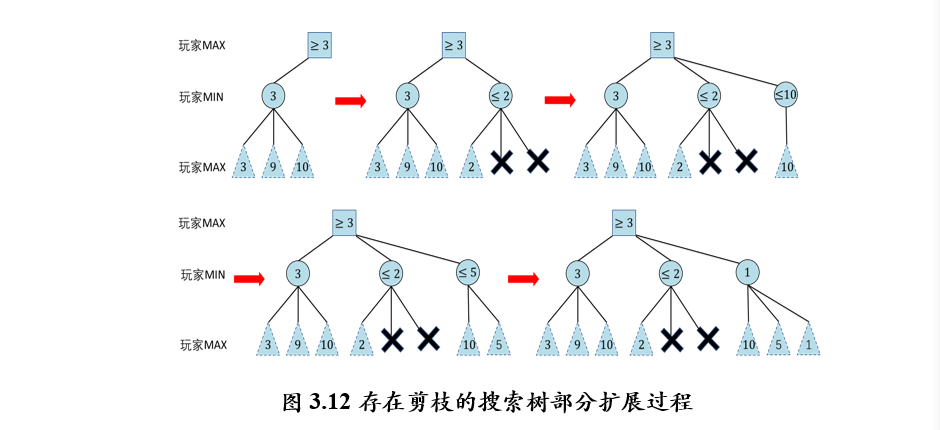
MIN节点\(m\):alpha剪枝
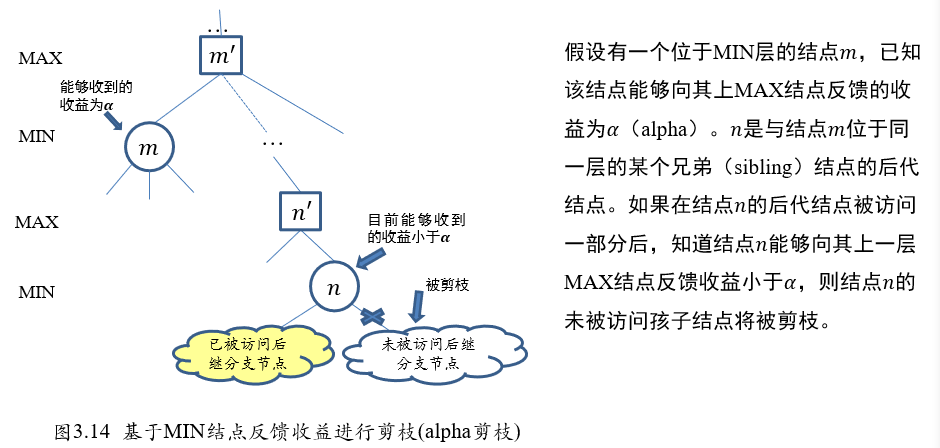
MAX节点\(m\):beta剪枝
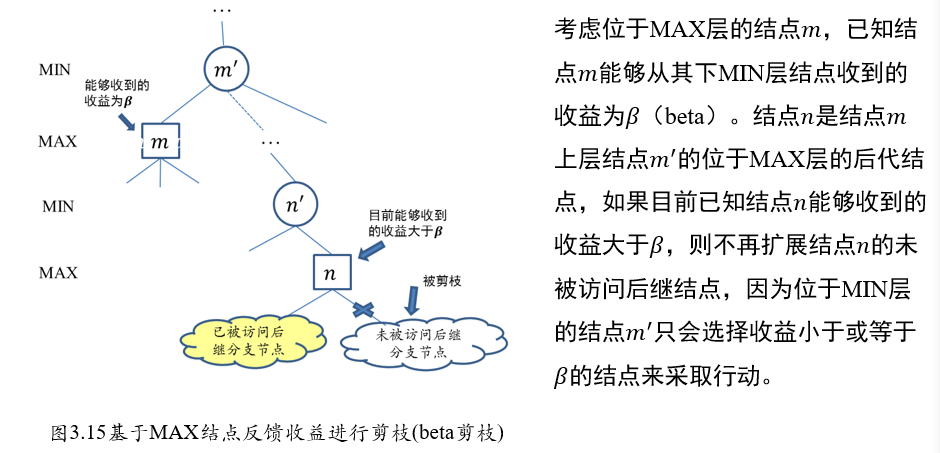



// 玩家MAX行动下, 当前的最优动作ans |
算法性能:

2.4 蒙特卡洛树搜索
2.4.1 问题定义

2.4.2 相关概念
核心:降低悔值函数的取值
悔值函数:期望T次操作的得分 - 实际T次操作的得分


2.4.3 贪心算法策略
在第t步,选择过去t-1步,平均的得分最高的赌博机
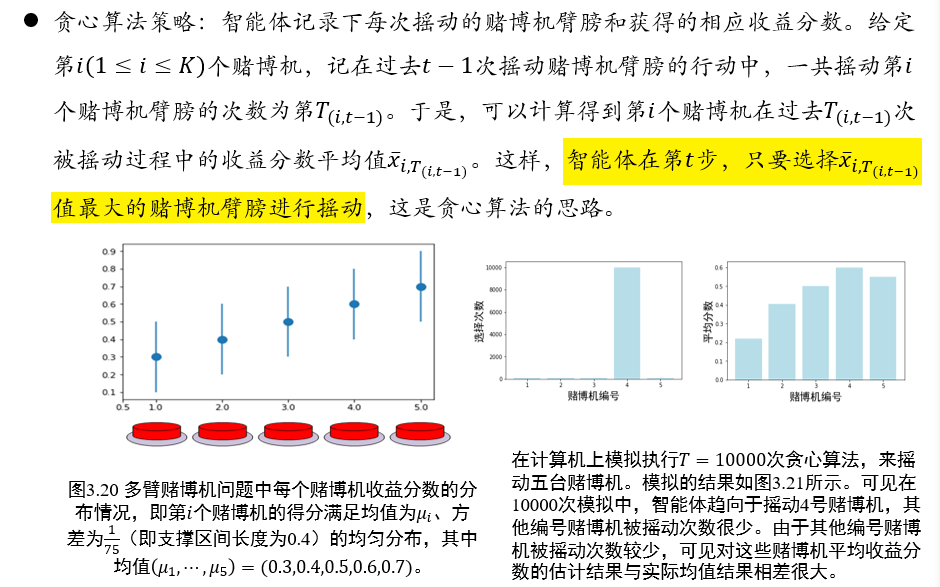

2.4.4 ε-贪心算法
在第t步,1-ε的概率取平均分最高,ε的概率取一个随机的赌博机

2.4.5 上限置信区间算法UCD1:Upper Confidence Bounds
估计每一个动作的奖励区间,优先选取上限高的动作
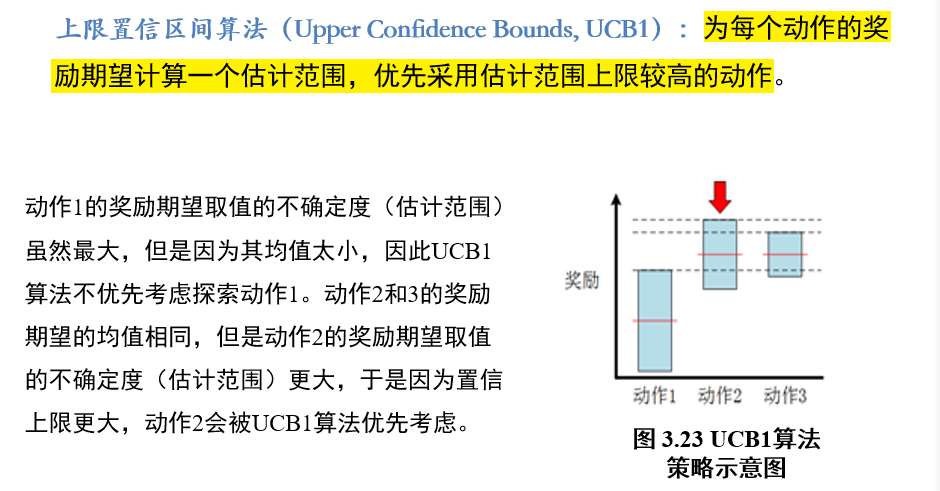


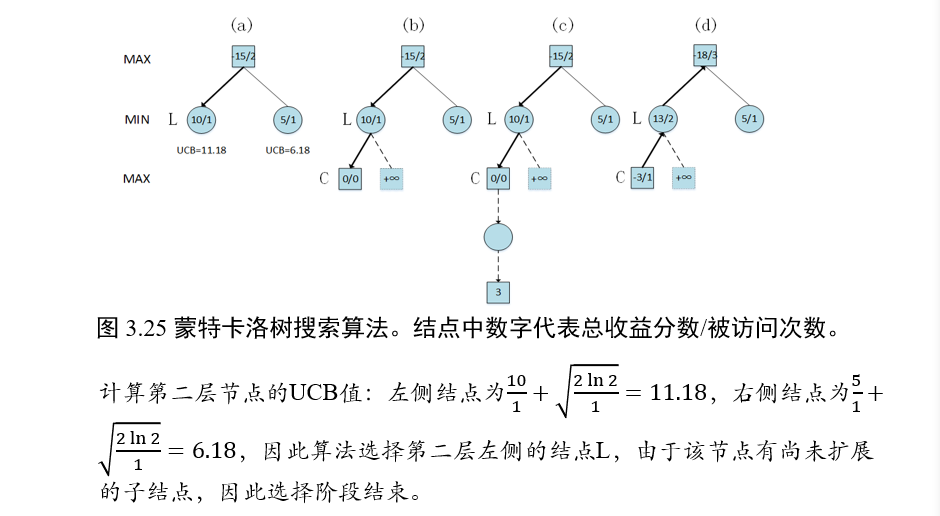
2.4.6 对抗搜索:蒙特卡洛树搜索
使用UCB1算法,预估下一步操作的收益


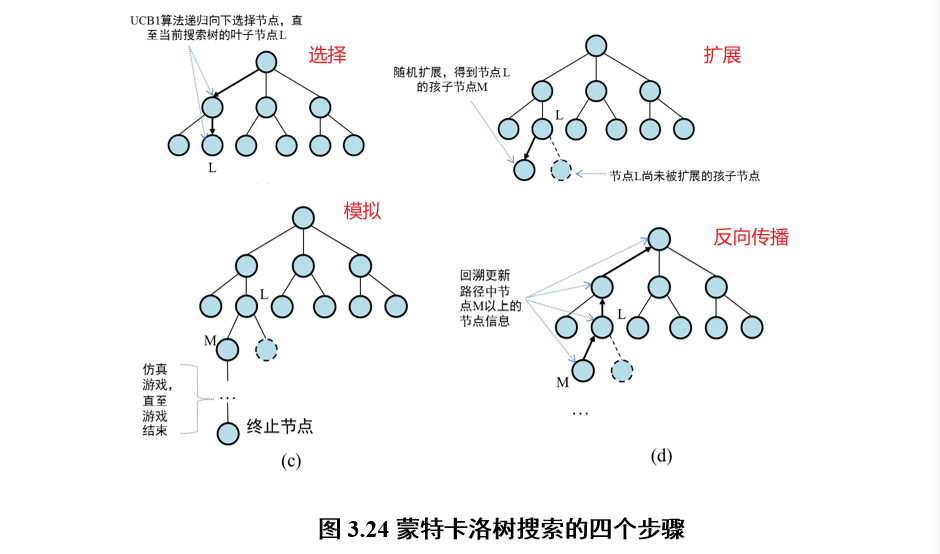
示例

三、监督学习
3.1 机器学习的基本概念
- 从原始数据中提取特征
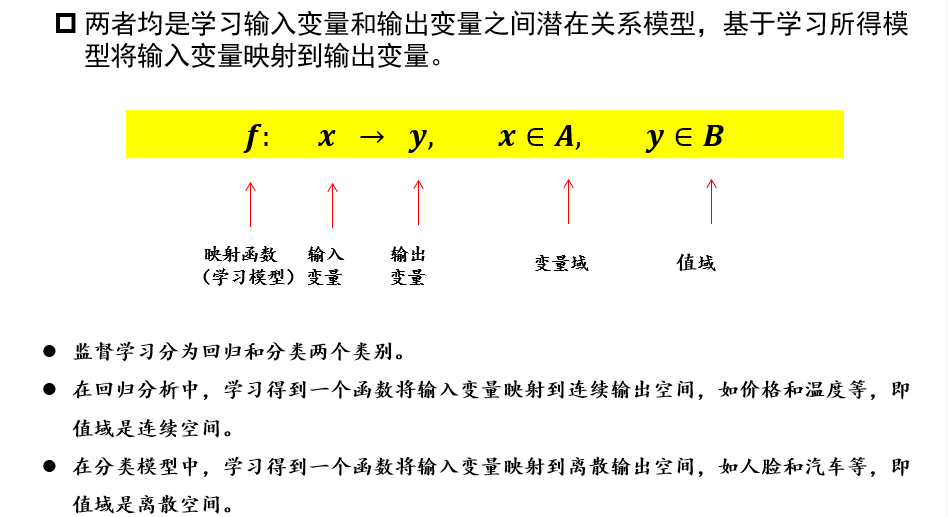
- 学习映射函数𝑓
- 通过映射函数𝑓将原始数据映射到语义任务空间,即寻找数据和任务目标之间的关系
3.1.1 机器学习的分类
- 监督学习:数据有标签,一般为回归/分类等任务
- 无监督学习:数据无标签,一般为聚类/若干降维任务
- 同一类物体之间总有一定的相似性
- 半监督学习:有的数据有标签,有的数据无标签
- 强化学习:序列数据决策学习,一般为从环境交互中学习
3.1.2 监督学习的重要元素
- 标注数据:标识了类别信息的数据,学什么
- 学习模型:如何学习到映射模型,如何学
- 损失函数:如何对学习结果进行度量,是否学到
没有免费午餐定理NFL:任何机器学习模型在所有问题上的性能都是相同的,其总误差和模型本身是没有关系的。一种算法(算法A)在特定数据集上的表现优于另一种算法(算法B)的同时,一定伴随着算法A在另外某一个特定的数据集上有着不如算法B的表现
3.1.3 监督学习
3.1.3.1 损失函数
- 设共有n个标注数据,第i个标记数据为\((x_i,y_i)\),其中\(x_i\)为样本数据,\(y_i\)是标注信息
- 设学习到的映射函数为\(f\),对\(x_i\)的预测结果为\(f(x_i)\)
- 损失函数即为计算\(y_i\)和\(f(x_i)\)之间的差值的函数
- 训练的目标是:在训练数据集上得到的损失之和最小,即\(min\sum_{i=1}^nLoss(f(x_i),y_i)\)
- 典型损失函数:
- 0-1损失函数:\(Loss(y_i,f(x_i))=\{1, f(x_i)\ne y_i;\ \ 0,f(x_i)=y_i\}\)
- 平方损失函数:\(Loss(y_i,f(x_i))=(y_i-f(x_i))^2\)
- 绝对损失函数:\(Loss(y_i,f(x_i))=|y_i-f(x_i)|\)
- 对数损失函数/对数似然损失函数:\(Loss(y_i,P(y_i|x_i))=-\log P(y_i|x_i)\)
3.1.3.2 训练数据与测试数据
- 训练精度:在测试数据集上的精度,因为在训练集上一定是100%通过的
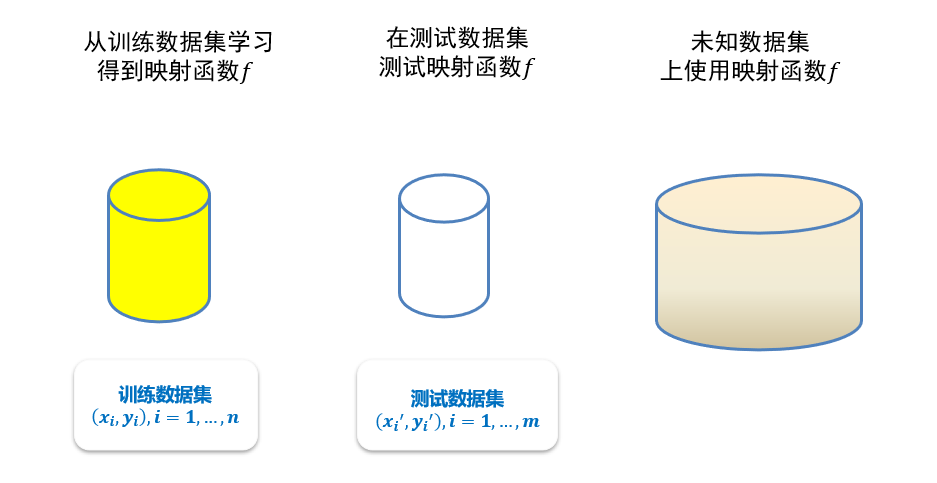
3.1.3.3 经验风险、期望风险
经验风险 empirical risk:训练集中数据产生的损失
经验风险越小说明学习模型对训练数据拟合程度越好
经验风险最小化ERM
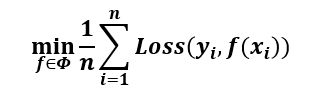
期望风险 expected risk:当测试集中存在无穷多数据时产生的损失
期望风险越小,学习所得模型越好
期望风险最小化ERM
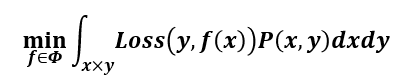
3.1.3.4 过学习 & 欠学习
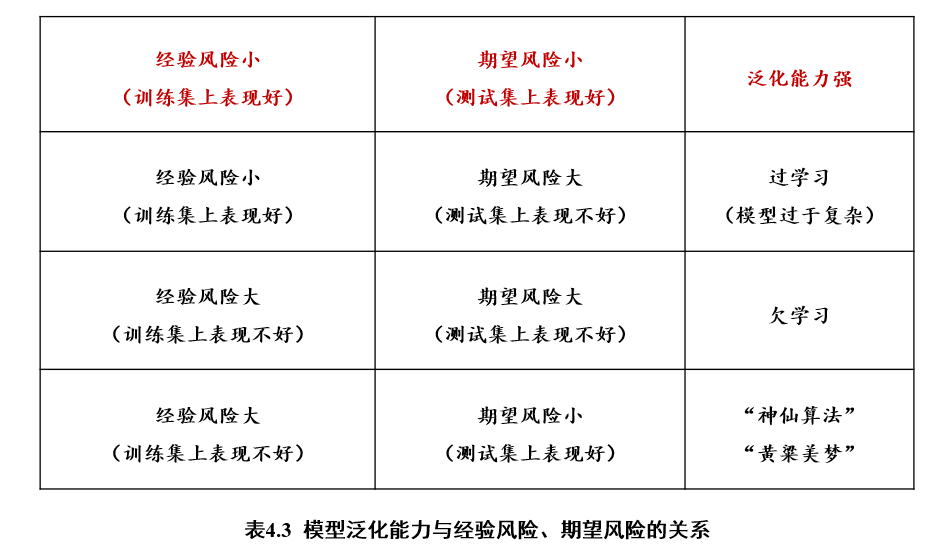
3.1.3.5 结构风险最小

3.1.3.6 判别模型 & 生成模型
判别模型:
- 建立输入到输出的映射函数:\(f(输入)=人脸\)
- 判断输入属于输出空间的概率有多大:\(P(人脸|输入)=0.99\)
生成模型:
学习联合概率分布\(P(X,Y)\)(通过似然概率\(P(X|Y)\)和类概率\(P(Y)\)的乘积来求取)
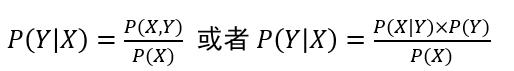
典型方法:贝叶斯方法、隐马尔科夫链
似然概率:计算导致样本\(X\)出现的模型参数值
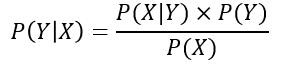
联合概率分布\(P(X,Y)\)、似然概率\(P(X|Y)\)求取很困难
3.2 回归分析
3.2.1 线性回归
- 回归分析:分析不同变量之间存在的关系
- 回归模型:刻画不同变量之间关系的模型
- 线性回归模型:回归模型是线性的
3.2.1.1 一元线性回归
一个变量,对另一个变量的影响
回归模型:\(f(x_i)=ax_i+b\)
要求:\(\frac{1}{N}\sum(y-\hat y)^2\)最小
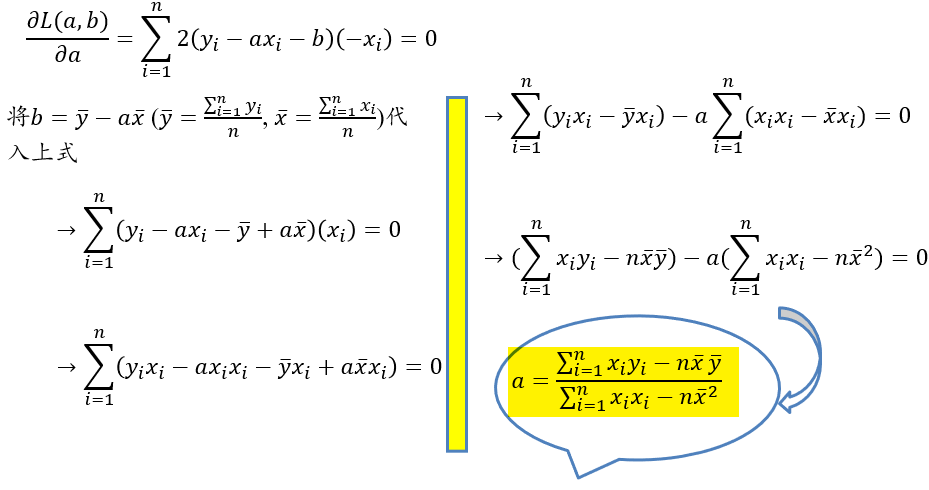
计算结果: \[ b=\overline{y}-a\overline{x}\\ a=\frac{\sum_{i=1}^{n}x_iy_i-n\overline{x}·\overline{y}}{\sum_{i=1}^{n}x_i^2-n\overline{x}^2} \]
计算过程:
3.2.1.2 多元线性回归
- 多个变量,对一个变量产生影响


3.2.1.3 logistics 回归/对数几率回归
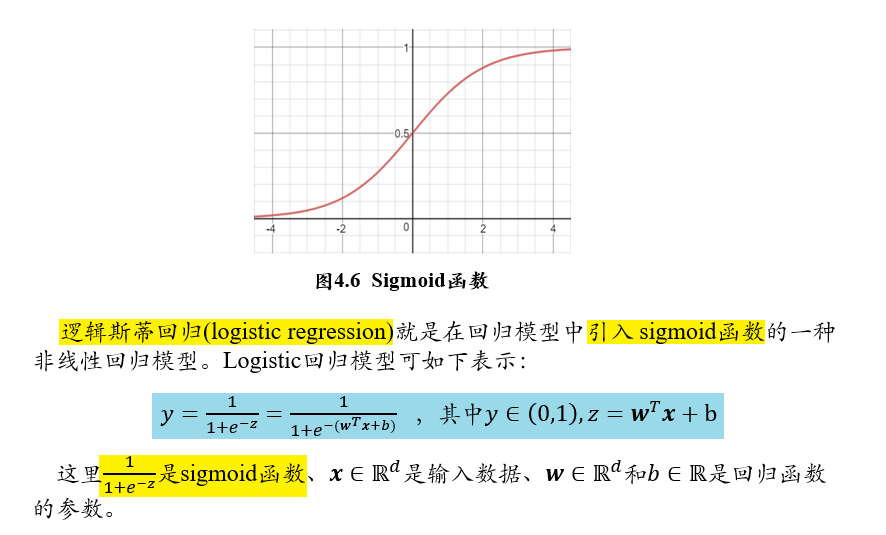

3.2.1.4 二分类问题


3.2.1.5 基于似然函数的参数优化

使用梯度下降公式,快速到达导数接近0的位置,出口为:
- 迭代次数到达预定次数
- 相邻两次差值小于某个值

3.2.1.6 MLE最大似然估计 & MAP最大后验概率估计

3.3 决策树
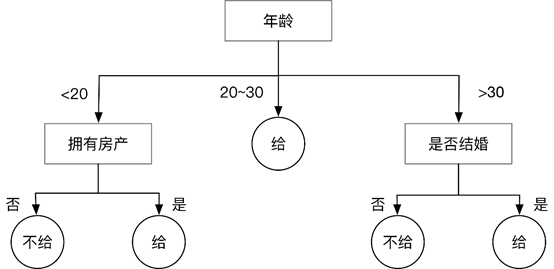
决策树是一种通过树形结构来进行分类的方法。
- 在决策树中,树形结构中每个非叶子节点表示对分类目标在某个属性上的一个判断,每个分支代表基于该属性做出的一个判断,最后树形结构中每个叶子节点代表一种分类结果
- 所以决策树可以看作是一系列以叶子节点为输出的决策规则
3.3.1 信息熵 E(D)
构建决策树时划分属性的顺序选择是重要的。
性能好的决策树随着划分不断进行,决策树分支结点样本集的“纯度”会越来越高,即其所包含样本尽可能属于相同类别,即E(D)尽可能小
假设有\(K\)个信息,组成了集合样本\(D\),第\(k\)个信息发生的概览为\(p_k(1\le k\le K)\),则这\(K\)个信息的信息熵为: \[ E(D)=-\sum_{k=1}^Kp_k\log_2\ p_k \]
- 其中,\(\sum_{k=1}^{K}p_k=1\)
\(E(D)\)值越小,表示\(D\)包含的信息越确定,即\(D\)的纯度越高
- 当\(p_k=1\)时,\(E(D)=0\),信息熵为0,即包含的信息量很小
年龄属性取值 ai “>30” “20~30” “<20” 对应样本数 |Di| 5 4 5 正负样本数量 (2+, 3-) (4+,0-) (3+,2-) 计算E(D):
3.3.2 信息增益 Gain(D,A)
得到信息熵后,可进一步计算使用某个特定属性A对原样本集D进行划分后的信息增益,计算公式为: \[ Gain(D,A)=E(D)-\sum_{i=1}^{n}\frac{|D_i|}{|D|}E(D_i) \]
- 其中,属性\(A\)将\(D\)划分为了\(n\)类,分别为\(D_1,...D_n\)
取信息增益最大的属性,作为决策树中靠近根节点的属性
3.3.3 信息熵和物理熵的区别
- 信息熵:描述信息的价值,某个信息发生概率越小,带来的信息量越大,信息熵就越大
- 香农用信息熵的概念来描述信源的不确定度
- 物理熵:表示分子状态混乱程度的物理量
- 熵越大,越失去次序,不确定性越大
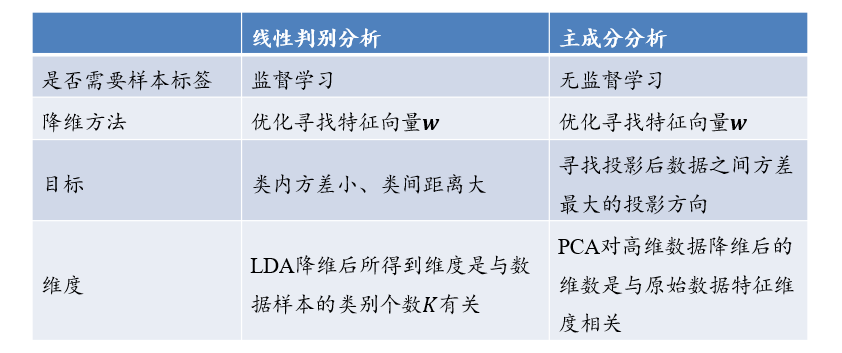
3.4 线性区别分析 LDA
Linear discriminant analysis
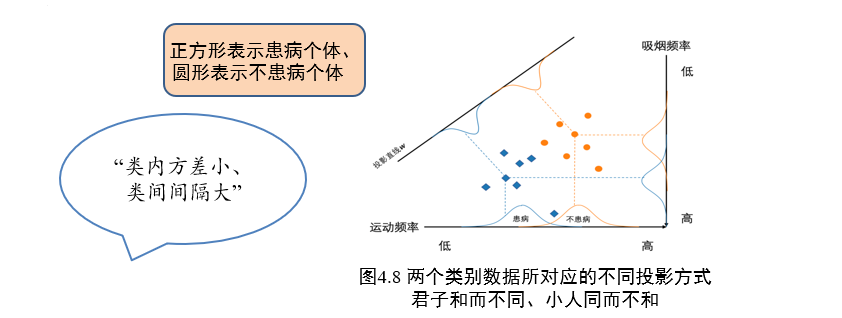
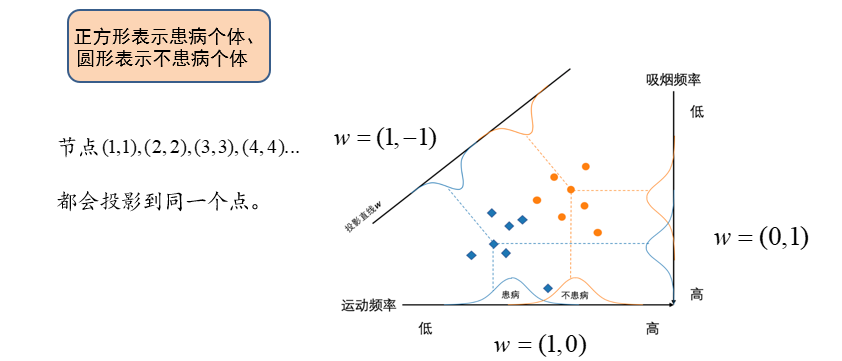
线性判别分析是一种基于监督学习的降维方法,也称为Fisher线性判别分析
- 对于一组具有标签信息的高维数据样本,LDA利用其类别信息,将其线性投影到一个低维空间
- 在低维空间中同一类别样本尽可能靠近,不同类别样本尽可能彼此远离,不要有交叉的部分
3.4.1 符号定义
- 设样本集为:\(D=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}\)
- \(x_i\in R^d\)表示样本,对应的标签为\(y_i\)
- \(y_i \in \{C_1,C_2,...,C_k\}\),表示一共有\(K\)类样本
- \(X\):所有样本构成的集合
- \(N_i\):第\(i\)个类别包含的样本个数
- \(X_i\):第\(i\)类样本的集合
- \(m\):所有样本的均值向量
- \(m_i\):第\(i\)类样本的均值向量
- \(\Sigma_i\):第\(i\)类样本的协方差矩阵,\(\Sigma_i=\sum_{x\in X_i}(x-m_i)(x-m_i)^T\)
3.4.2 二分类问题
\(K=2\)时,表示二分类问题,其样本的标签为\(\{C_1,C_2\}\),并通过线性函数\(y(x)=w^Tx\ \ \ (w\in R^n)\)投影到一维空间
- \(w\):系数矩阵,需要通过数据学习
计算系数矩阵\(w\)的方法: \[
w=S_w^{-1}(m_2-m_1)=(\Sigma_1+\Sigma_2)^{-1}(m_2-m_1)
\]




投影过程中,保持方差结构不变:即原来两类包含的是某些样本,投影完之后依旧分别包含这些样本
3.4.3 多分类问题


3.4.4 线性判别分析的降维步骤
- 计算数据样本集中,每个类别样本的均值\(m_i\)
- 计算类内散度矩阵\(S_w\)、类间散度矩阵\(S_b\)
- 根据\(S_w^{-1}S_bW=\lambda W\),求解\(S_w^{-1}S_b\)对应的前\(r\)个最大特征根对应的特征向量\((w_1,w_2,...,w_r)\),构成投影矩阵\(W\)
- 通过矩阵\(W\)将每个样本映射到低维空间,实现特征降维
3.5 Ada Boosting
adaptive boosting,自适应提升
- 对于一个复杂的分类任务,可以将其分解为若干子任务,然后将若干子任务完成方法综合,最终完成该复杂任务
- 将若干个弱分类器(weak classifiers)组合起来,形成一个强分类器(strong classifier)
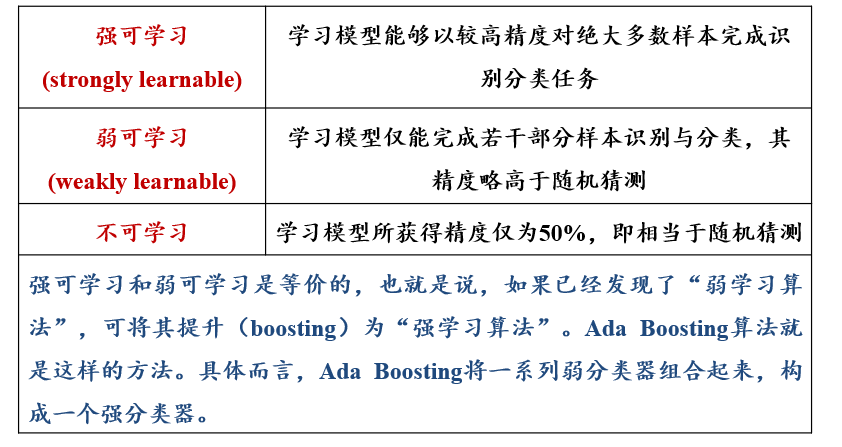
3.5.1 计算学习理论:霍夫丁不等式
- 学习任务:统计某个电视节目在全国的收视率
- 方法:不可能去统计整个国家中每个人是否观看电视节目、进而算出收视率。只能抽样一部分人口,然后将抽样人口中观看该电视节目的比例作为该电视节目的全国收视率
- 霍夫丁不等式:全国人口中看该电视节目的人口比例\(x\)与抽样人口中观看该电视节目的人口比例\(y\)满足关系:\(P(|x-y|\ge \epsilon) \le
2e^{-2N\epsilon^2}\)
- \(N\):采样人口总数
- \(\epsilon \in(0,1)\):设定的可容忍误差范围
- 当\(N\)足够大时,“全国人口中电视节目收视率”与“样本人口中电视节目收视率”差值超过误差范围\(\epsilon\)的概率非常小
3.5.2 计算学习理论:概率近似正确 PAC
probably approximately correct
- 对于统计电视节目收视率这样的任务,可以通过不同的采样方法(即不同模型)来计算收视率。每个模型会产生不同的误差
- 任务:得到完成该任务的若干“弱模型”,将这些弱模型组合起来形成一个“强模型”
3.5.3 Ada Boosting:思路描述
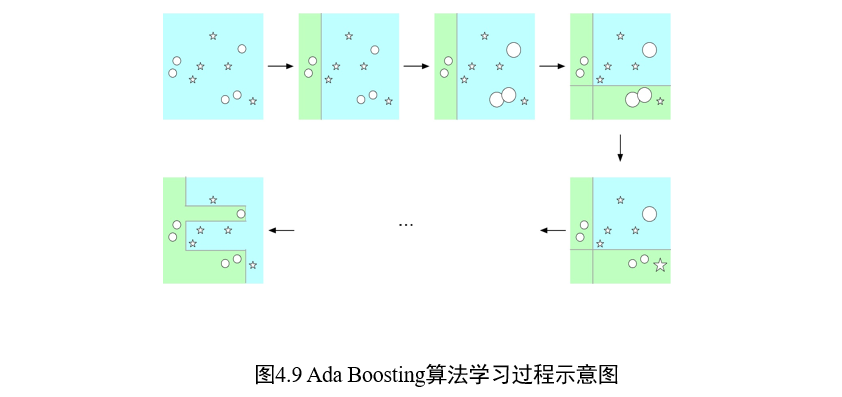
两个核心问题:
- 在每个弱分类器学习过程中:改变训练数据的权重
- 提高在上一轮中分类错误样本的权重
- 即关注上一个弱分类器无法解决的结果,进行优化
- 如何将一系列弱分类器组合成强分类器:加权多数表决方法
- 提高分类误差小的弱分类器的权重,让其在最终分类中起到更大作用
- 减少分类误差大的弱分类器的权重,让其在最终分类中仅起到较小作用
3.5.4 Ada Boosting:算法描述
3.5.4.1 数据样本权重初始化
- 给定包含\(N\)个标注数据的训练集合\(\Gamma\)
- \(\Gamma=\{(x_1,y_1),...,(x_N,y_N)\}\),其中\(x_i\in X\sub R^n, y_i\in Y=\{-1,1\}\)
- 初始化每个训练样本的权重:
- \(D_1=(w_{11},...,w_{1N}),\ w_{1i}=\frac{1}{N}\)
3.5.4.2 第m个弱分类器的训练
对于\(m=1,2,...M\)
- 使用具有分布权重\(D_m\)的训练数据,学习得到第m个弱分类器\(G_m\)
- \(G_m(x): X \rightarrow \{-1,1\}\)
- 计算\(G_m(x)\)在训练数据集上的分类误差:
- \(err_m=\sum_{i=1}^Nw_{mi}\ I(G_m(x_i)\neq y_i)\)
- 其中,\(I(G_m(x_i)\neq y_i)\)表示:当\(G_m(x_i)\neq y_i\)时为1,否则为0
- 计算\(G_m(x)\)的权重:弱分类器的权重和不为1
- \(\alpha_m=\frac{1}{2}\ln \frac{1-err_m}{err_m}\)
- 更新训练样本数据的分布权重:每一轮样本的权重和为1
- \(D_{m+1}=w_{m+1,i}=\frac{w_{m,i}}{Z_m}e^{-\alpha_my_iG_m(x_i)}\)
- 其中,\(Z_m\)是归一化因子,使得\(D_{m+1}\)为概率分布
- \(Z_m=\sum_{i=1}^Nw_{m,i}e^{-\alpha_my_iG_m(x_i)}\)
3.5.4.3 弱分类器组合成强分类器
- 以线性加权形式来组合弱分类器\(f(x)\):\(f(x)=\sum_{i=1}^M\alpha_mG_m(x)\)
- 得到强分类器\(G(x)\):\(G(x)=sign(f(x))=sign(\sum_{i=1}^M\alpha_mG_m(x))\)
3.5.5 Ada Boosting:算法解释




3.5.6 Ada Boosting:回看霍夫丁不等式

3.5.7 Ada Boosting:优化目标

3.5.8 回归和分类的区别
(不考)3.6 支持向量机
(不考)3.6.1 VC维与结构风险最小化
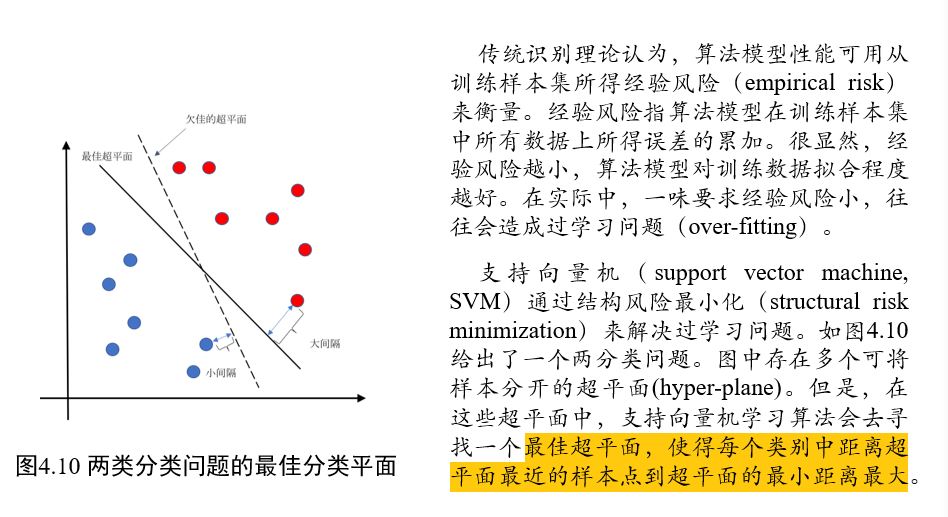
h:反应机器复杂程度的VC维,要求机器本身不要太复杂

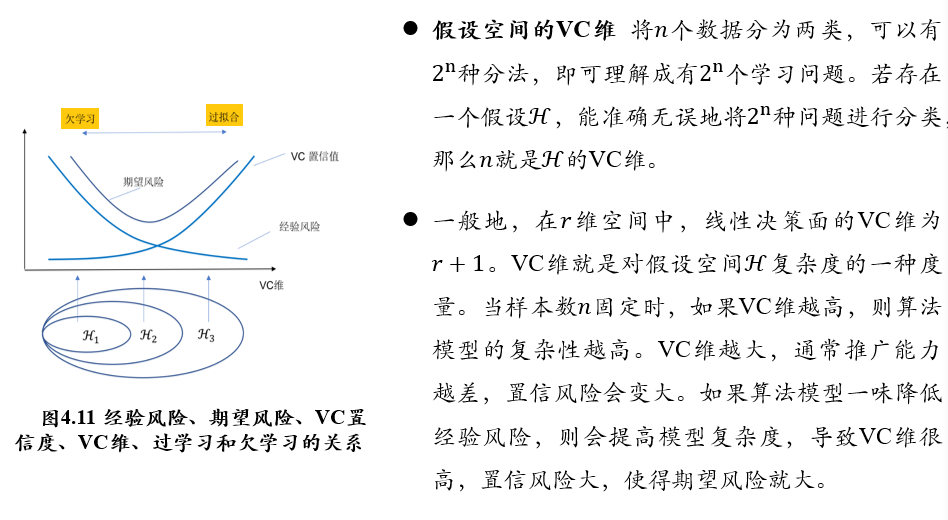

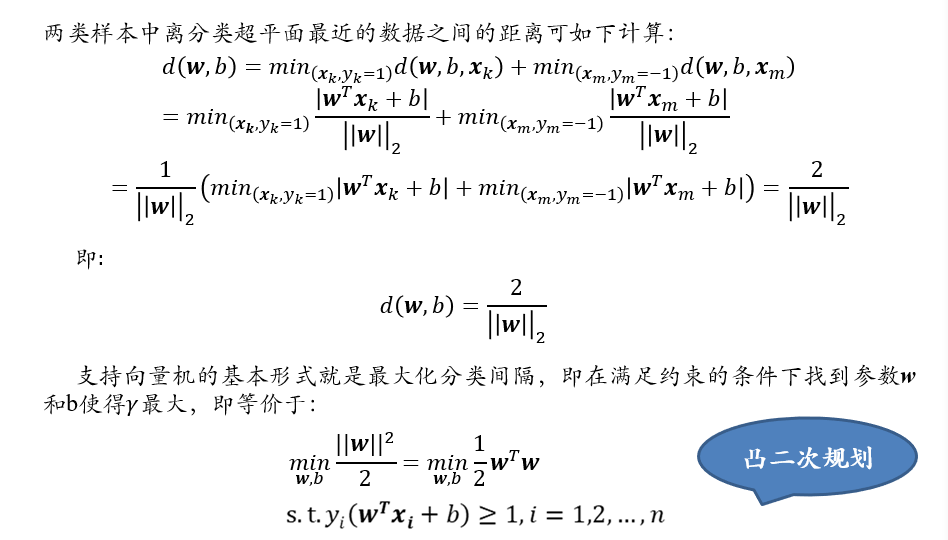
(不考)3.6.2 线性可分支持向量机
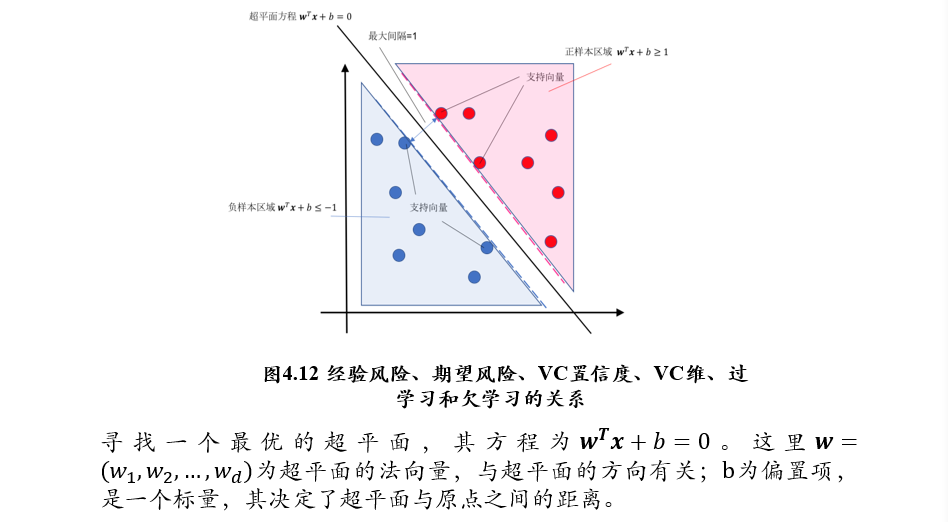
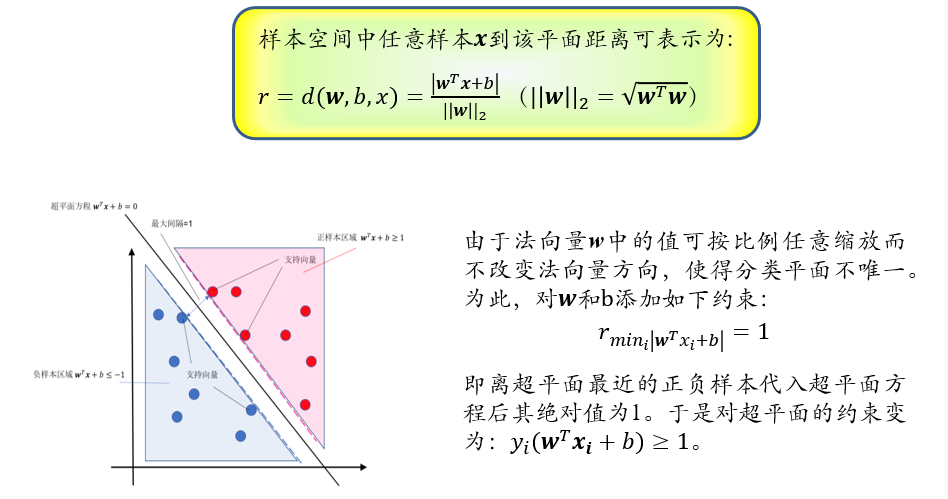
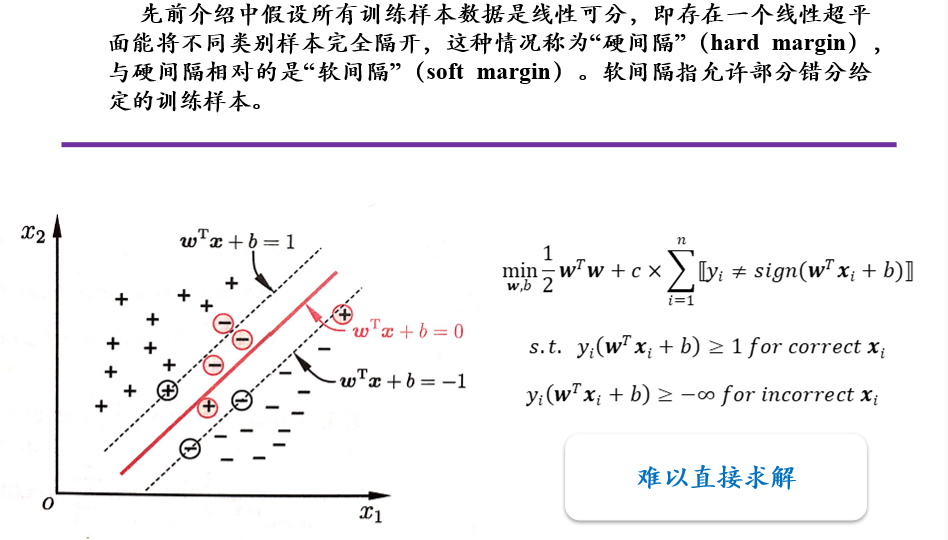
(不考)3.6.3 松弛变量,软间隔与hinge损失函数

(不考)3.7 生成学习模型
生成学习方法从数据中学习联合概率分布\(P(X,C)\),然后求出条件概率分布\(P(C|X)\)作为预测模型,即\(P(c_i|x)=\frac{P(x,c_i)}{P(x)}\)
- \(P(x,c_i)=P(x|c_i)×P(c_i)\)
- \(P(x|c_i)\):似然概率
- \(P(c_i)\):先验概率
- \(P(c_i|x)=\frac{P(x,c_i)}{P(x)}=\frac{P(x|c_i)×P(c_i)}{P(x)}\)
- \(P(c_i|x)\):后验概率,表示样本\(x\)属于类别\(c_i\)的概率
- \(P(x,c_i)\):联合概率

生成式学习:
- 学习某个输入与某个类别同时出现的概率,根据某个输入出现的概率,计算某个输入对应某个类别的概率
- 模拟了数据生成的方法
- 但是联合概率难以学习,因为训练数据中输入与类别没有同时出现,不代表以后永远不会同时出现
- 以购买商品为例:
- 联合概率\(P(x,c_i)\):某个人购买了某个商品的概率
- 似然概率\(P(x|c_i)\):某个商品让某个人购买的概率,某个人没有买,但是与之类似的人买过,此时可以转换为某个商品让某个人购买的概率有多大
- 先验概率\(P(c_i)\):某个商品出现的概率,即在所有卖出的商品中,该商品出现的概率
判别式学习:直接学习某个输入对应某个类别的概率
四、无监督学习
无监督学习从非标注样本出发来学习数据的分布,这是一个异常困难的工作。由于无法利用标注信息,因此在无监督学习只能利用假设数据具有某些结构来进行学习。正如拉普拉斯所言“概率论只不过是把常识用数学公式表达了出来”,无监督学习就是把预设数据具有某种结构作为一种“知识”来指导模型的学习。
4.1 K均值聚类
输入:n个数据,无标注信息
输出:k个聚类结果
目的:将n个数据聚类到k个集合(类簇)
4.1.1 算法描述
定义:
- n个m维数据\(\{x_1,x_2,...x_n\}, x_i\in R^m\)
- 两个m维数据之间的欧氏距离为:\(d(x_i,x_j)=\sqrt{(x_{i1}-x_{j1})^2+(x_{i2}-x_{j2})^2+...+(x_{im}-x_{jm})^2}\)
- 欧氏距离并不一定能够刻画语义上的相似性
- 但是总要找一个函数表示数据之间的相似性,这里就以欧氏距离为例
- 聚类集合数目:\(k\)
4.1.1.1 初始化聚类质心
- 初始化\(k\)个聚类质心\(c=\{c_1, c_2,...,c_k\}\),\(c_j\in R^m,1\le j \le k\)
- 每个聚类质心\(c_j\)所在的集合记为\(G_j\)
4.1.1.2 将每个待聚类数据放入唯一一个聚类集合中
- 计算待聚类数据\(x_i\)和质心\(c_j\)之间的欧氏距离\(d(x_i,c_j)\),\(1\le i\le n, 1\le j \le k\)
- 将每个\(x_i\)放入与之距离最近的聚类质心所在聚类集合中,即
\[ argmin_{c_{j\in C}}d(x_i,c_j) \]
4.1.1.3 根据聚类结果,更新聚类质心
- 聚类\(G_j\)的新的聚类质心\(c_j\)为:
\[ c_j=\frac{1}{|G_j|}\sum_{x_i\in G_j}x_i \]
4.1.1.4 算法循环迭代,直到满足条件
- 在新的聚类质心基础上,根据欧氏距离的大小,将每个待聚类数据放入唯一一个聚类集合中
- 根据聚类结果,更新聚类质心
- 重复上述两个步骤,直到满足一下任意一个条件:
- 前后两次迭代中,聚类质心基本保持不变
- 此时算法收敛,结果相对来说比较好
- 迭代次数达到上限
- 此时算法不收敛,可能是由于欧氏距离并不能很好的刻画数据的相似度
- 前后两次迭代中,聚类质心基本保持不变
4.1.2 另一个视角:最小化每个类簇的方差
方差:计算变量(观察值)与样本平均值之间的差异 \[ argmin_{G}\sum_{i=1}^k\sum_{x \in G_i}|x-G_i|^2=argmin_{G}\sum_{i=1}^k|G_i|Var\ G_i \] 第\(i\)个类簇的方差: \[ var(G_i)=\frac{1}{|G_i|}\sum_{x \in G_i}|x-G_i|^2 \]
- 欧氏距离与方差量纲相同
- 最小化每个类簇方差将使得最终聚类结果中每个聚类集合中所包含数据呈现出来差异性最小
4.1.3 K均值聚类算法的不足
- 需要事先确定聚类数目,很多时候我们并不知道数据应被聚类的数目
- 需要初始化聚类质心,初始化聚类中心对聚类结果有较大的影响
- 算法是迭代执行,时间开销非常大
- 欧氏距离假设数据每个维度之间的重要性是一样的
4.2 主成分分析 PCA
Principle Component Analysis
主成分分析是一种特征降维方法(与线性区别分析的目的是一样的)
- 要尽可能将投影后的数据打散,即方差最大
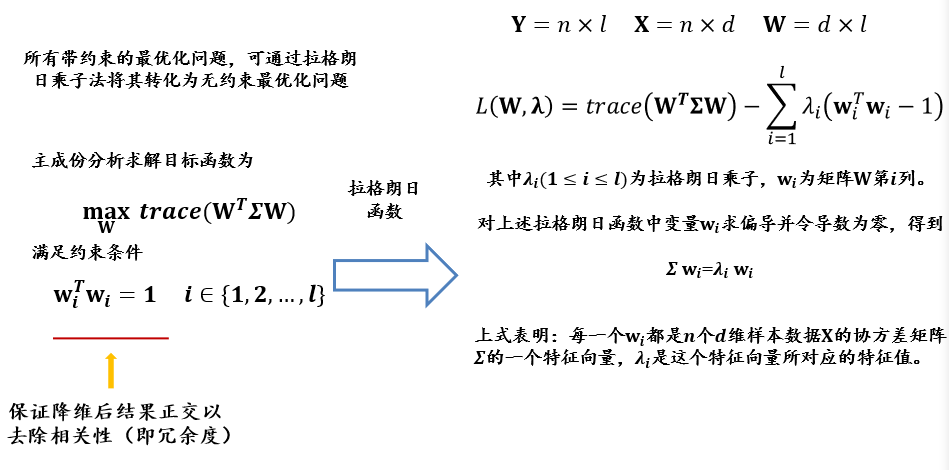
- 设原数据为\(X_{n×d}\),投影后的数据为\(Y_{n×l}\),投影矩阵为\(W_{d×l}\),则有\(Y=XW\)
- 投影矩阵\(W_{d×l}\)为:协方差矩阵\(\Sigma\)前\(l\)个最大的特征根对应的特征向量\(_{d×1}\)组成的矩阵\(_{d×l}\)
4.2.1 相关概念
假设有n个数据,记为\(X=\{x_i\}, i=1,...n\)
- 方差:描述样本数据的波动程度 \[ Var(X)=\frac{1}{n}\sum_{i=1}^n(x_i-u)^2\\ u=\frac{1}{n}\sum_{i=1}^n x_i \]
假设有n个二维变量数据,记为\((X,Y)=\{(x_i,y_i)\}, i=1,...n\)
协方差:衡量两个维度之间的相关度
- 协方差\(cov(X,Y)>0\)时:正相关
- 协方差\(cov(X,Y)<0\)时:负相关
- 协方差\(cov(X,Y)=0\)时:线性意义下不相关
\[ cov(X,Y)=\frac{1}{n}\sum_{i=1}^n(x_i-E(X))(y_i-E(Y))\\ E(X)=\frac{1}{n}\sum_{i=1}^nx_i,\ \ E(Y)=\frac{1}{n}\sum_{i=1}^ny_i \]
皮尔逊相关系数:将协方差归一化
- \(|corr(X,Y)|\le1\)
- \(|corr(X,Y)=1|\) <=> 存在常数\(a,b\),使得\(Y=aX+b\)
- \(corr(X,Y)=corr(Y,X)\)
\[ corr(X,Y)=\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}=\frac{Cov(X,Y)}{\sigma_x\sigma_y} \]
相关性与独立性:
- 如果\(X\)与\(Y\)线性不相关,则\(|corr(X,Y)|=0\)
- 如果\(X\)与\(Y\)独立,则\(|corr(X,Y)|=0\),且\(X\)与\(Y\)不存在任何线性、非线性关系
- 独立一定不相关,但不相关不一定独立
4.2.2 算法动机
- 在数理统计中,方差被经常用来度量数据和其数学期望(即均值)之间偏离程度,这个偏离程度反映了数据分布结构
- 在许多实际问题中,研究数据和其均值之间的偏离程度有着很重要的意义
- 在降维之中,需要尽可能将数据向方差最大方向进行投影,使得数据所蕴含信息没有丢失,彰显个性。如左下图所示,向𝒚方向投影(使得二维数据映射为一维)就比向𝒙方向投影结果在降维这个意义上而言要好;右下图则是向黑斜线方向投影要好。
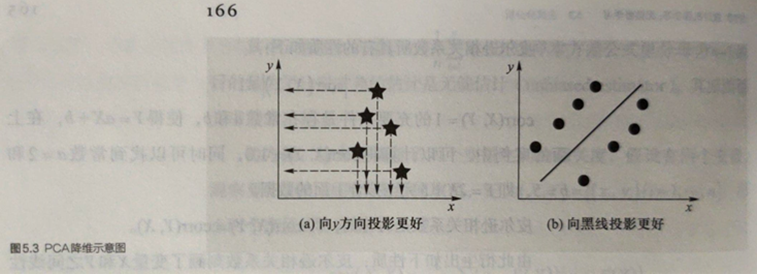
- 主成分分析思想是将𝒏维特征数据映射到𝒍维空间(𝒏 ≫ 𝒍),去除原始数据之间的冗余性(通过去除相关性手段达到这一目的)。
- 将原始数据向这些数据方差最大的方向进行投影。一旦发现了方差最大的投影方向,则继续寻找保持方差第二的方向且进行投影。
- 将每个数据从𝒏维高维空间映射到𝒍维低维空间,每个数据所得到最好的𝒌维特征就是使得每一维上样本方差都尽可能大。
4.2.3 算法描述
- 假设有\(𝑛\)个\(𝑑\)维样本数据所构成的集合\(𝐷=\{x_1,x_2,…,x_n\}\),其中\(x_i(1≤i≤n)∈R^d\)
- 集合\(𝐷\)可以表示成矩阵\(X_{𝑛×𝑑}\)
- 假定每一维度的特征均值均为零(已经标准化)
- 主成分分析的目的是求映射矩阵\(W_{𝑑×𝑙}\)
- 给定一个样本\(x_𝑖\),可将$x_𝑖 \(从\)𝑑\(维空间如下映射到\)𝑙$维空间: \((x_i)_{1×d}(W)_{d×l}\)
- 将所有降维后数据用\(Y\)表示,有\(Y=XW\)
- \(Y\):降维结果,\(n×l\)
- \(X\):原始数据,\(n×d\)
- \(W\):映射矩阵,\(d×l\)
投影矩阵\(W_{d×l}\)为:协方差矩阵\(\Sigma\)前\(l\)个最大的特征根对应的特征向量\(_{d×1}\)组成的矩阵\(_{d×l}\)
最优方差为:协方差矩阵\(\Sigma\)前\(l\)个最大的特征根之和
4.2.4 其他常用降维方法
- 非负矩阵分解 NMF:non-negative matrix factorization
- 多为尺度法MDS:Metric multidimensional
- 局部先行嵌入LLE:Locally Linear Embedding
4.3 特征人脸方法
4.3.1 动机
- 特征人脸方法是一种应用主成份分析来实现人脸图像降维的方法
- 其本质是用一种称为“特征人脸(eigenface)”的特征向量按照线性组合形式来表达每一张原始人脸图像,进而实现人脸识别
- 由此可见,这一方法的关键之处在于如何得到特征人脸
- 用特征人脸表示人脸,而非用像素点表示人脸
4.3.2 算法描述
将每幅人脸图像转化为列向量
- 例如:将一幅32×32的人脸图像转化为1024×1的列向量

执行PCA特征降维

每个人脸特征向量\(w_i\)与原始人脸数据\(x_i\)的维数是一样的,均为\(1024\)
可将每个特征向量还原为𝟑𝟐×𝟑𝟐的人脸图像,称之为特征人脸,因此可得到\(l\)个特征人脸

将每幅人脸分别与特征人脸做矩阵乘法,得到一个相关系数
每幅人脸得到\(l\)个相关系数 => 每幅人脸从1024维约简到\(l\)维
由于每幅人脸是所有特征人脸的线性组合,因此就实现人脸从“像素点表达”到“特征人脸表达”的转变。每幅人脸从1024维约减到\(l\)维
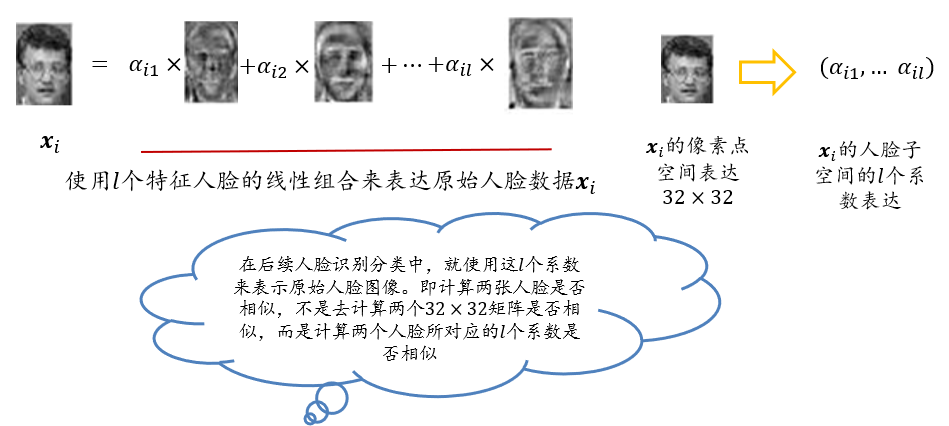
4.3.3 其他人脸表达的方法:聚类、PCA、非负矩阵分解

4.4 潜在语义分析
latent semantic analysis、latent semantic indexing
潜在语义分析(LSA或LSI):又叫隐形语义分析
- 是一种从海量文本数据中学习单词-单词、单词-文档以及文档-文档之间隐性关系,进而得到文档和单词表达特征的方法
- 基本思想:综合考虑某些单词在哪些文档中同时出现,以此来决定该词语的含义与其他的词语的相似度
4.4.1 潜在语义分析思想
- 先构建一个单词-文档(term-document)矩阵A
- 进而寻找该矩阵的低秩逼近(low rank approximation),来挖掘单词-单词、单词-文档以及文档-文档之间的关联关系
4.4.2 分析过程
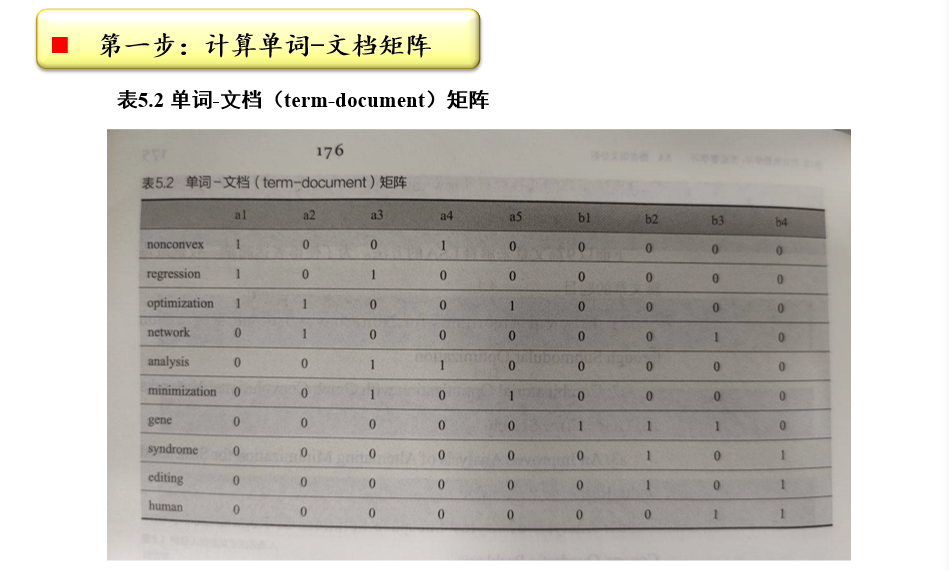
计算单词-文档矩阵:\(A_{m×n}\)
- 某个term在某个document中出现了几次,对应的值即为几
- 也可以统计:TF×iDF,TF在某个文章中出现的频率,DF在所有文章中出现的频率
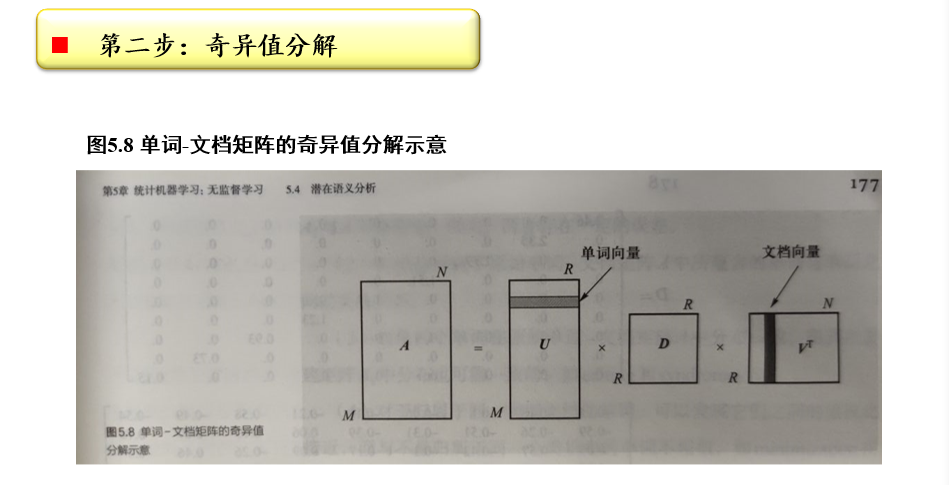
奇异值分解:\(A_{m×n}=U_{m×r}D_{r×r}V^T_{r×n}\)
- SVD分解:将矩阵\(A_{m×n}\)分解为三个矩阵的的乘积\(U_{m×r}D_{r×r}V^T_{r×n}\)
- \(D_{r×r}=diag(\sigma_1,\sigma_2,...,\sigma_r)\),是\(A_{m×n}\)的所有奇异值,也是\(AA^T\)特征值的非负平方根,满足\(\sigma_1\ge\sigma_2\ge,...,\ge\sigma_r>0\)

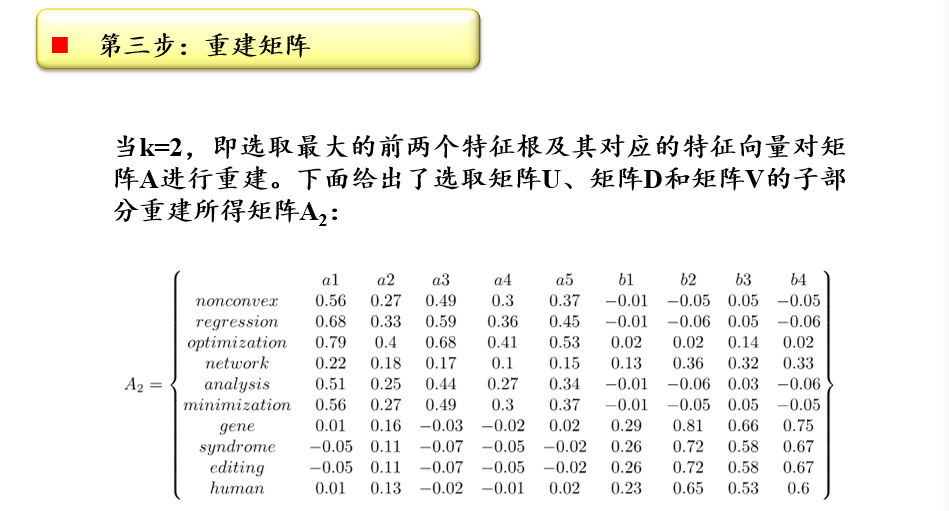
重建矩阵:\(A_{k}=U_{m×k}D_{k×k}V^T_{k×n}\)
- 选取前k个特征根及其对应的特征向量,对矩阵A进行重建
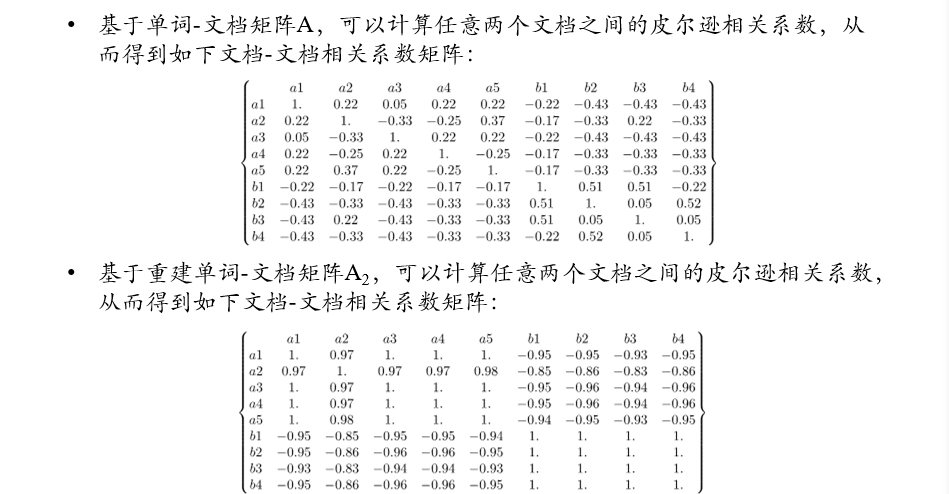
挖掘语义关系
- 根据由主题重建出来的矩阵\(A_k\),计算皮尔逊相关系数
- 通过分解和重建,可以将主题相关的两个文档之间的相关系数变得更大

4.5 期望最大化算法 EM
expectation maximization
4.5.1 模型参数估计
最大似然估计:

最大后验估计:

无论是最大似然估计算法或者是最大后验估计算法,都是充分利用已有数据,在参数模型确定(只是参数值未知)情况下,对所优化目标中的参数求导,令导数为0,求取模型的参数值
在解决一些具体问题时,难以事先就将模型确定下来,然后利用数据来求取模型中的参数值。在这样情况下,无法直接利用最大似然估计算法或者最大后验估计算法来求取模型参数
4.5.2 期望最大化算法
Expectation Maximization
- EM算法是一种重要的用于解决含有隐变量(latent variable)问题的参数估计方法
- EM算法分为求取期望(E步骤,expectation)和期望最大化(M步骤,maximization)两个步骤
- 在EM算法的E步骤时,先假设模型参数的初始值,估计隐变量取值
- 在EM算法的M步骤时,基于观测数据、模型参数和隐变量取值一起来最大化“拟合”数据,更新模型参数
- 基于所更新的模型参数,得到新的隐变量取值(EM算法的 E 步),然后继续极大化“拟合”数据,更新模型参数(EM算法的M步)
- 以此类推迭代,直到算法收敛,得到合适的模型参数
4.5.3 EM示例:二硬币投掷例子
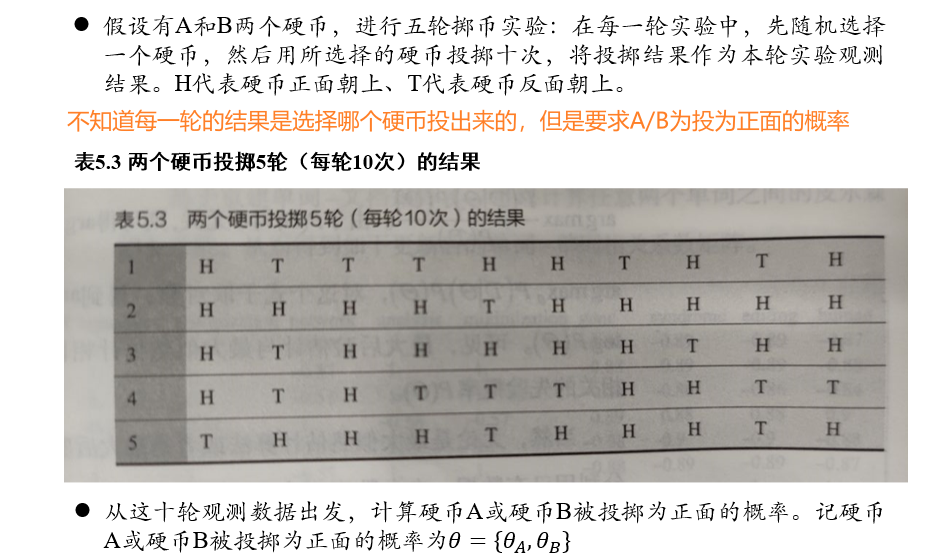
目标/模型参数:求A/B为正面的概率\(\{\theta_A,\theta_B\}\)
隐变量:某一轮是A投出的,还是B投出的
初始化模型参数\(\{\theta_A,\theta_B\}\),即可得到得出某一轮结果是由A/B投出的概率

然后即可得某一轮结果中,A/B投为正/反面的期望次数
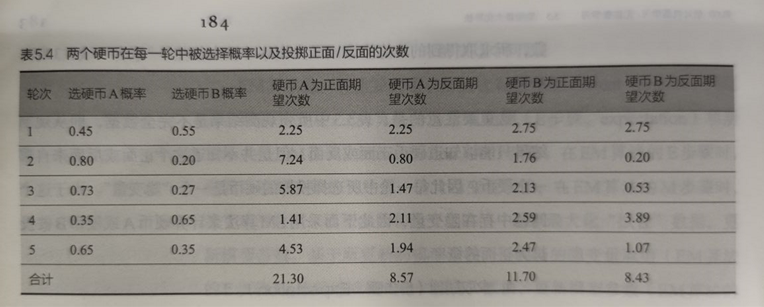

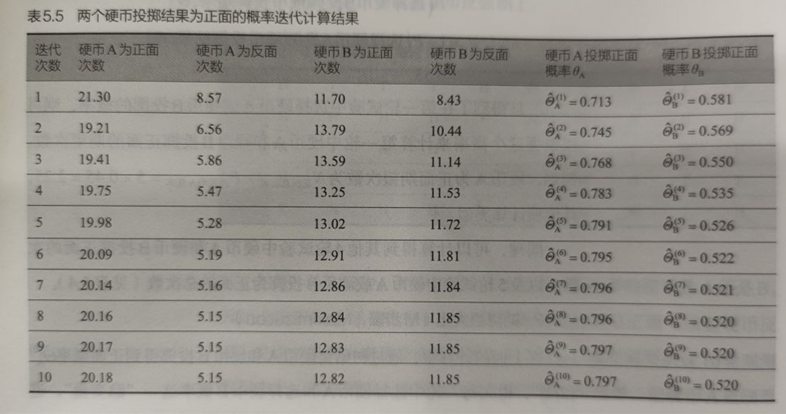
根据之前的计算结果,得出A/B投为正/反面的期望次数,从而更新A/B分别投正面的概率

不断迭代上述过程,直到算法收敛,就可以得到A/B投为正面的概率
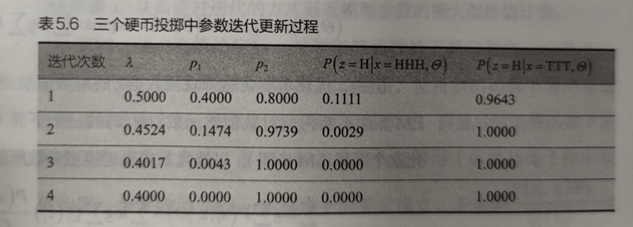
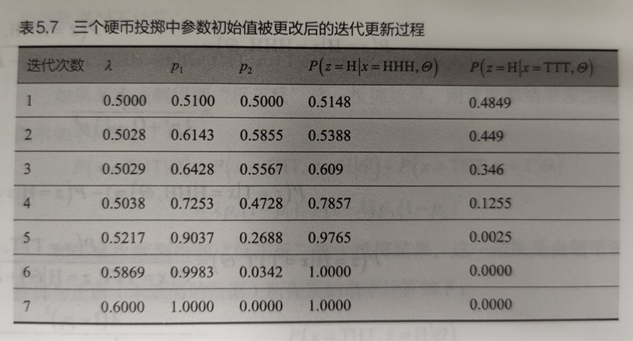
4.5.4 EM示例:三硬币投掷例子

目标/模型参数:求0/1/2为正面的概率\(\{\lambda,p_1,p_2\}\)
隐变量:硬币0的投掷结果
初始化模型参数\(\{\lambda,p_1,p_2\}\):通过假设每一次0号硬币的结果得出


迭代更新模型参数值,直到收敛
4.5.5 EM算法的一般形式
对n个相互独立的样本\(X=\{x_1,x_2,...,x_n\}\)及其对应的隐变量\(Z=\{z_1,z_2,...,z_n\}\),在假设样本的模型参数为\(\Theta\)前提下,观测数据\(x_i\)的概率为\(P(x_i|\Theta)\),完全数据\((x_i,z_i)\)的似然函数为\(P(x_i,z_i|\Theta)\)
在这种表示基础上,优化目标为:求解合适的\(\Theta\)和\(Z\),使得对数似然函数最大: \[ (\Theta,Z)=argmax_{\Theta,Z}L(\Theta,Z)=argmax_{\Theta,Z}\sum_{i=1}^nlog\sum_{z_i}P(x_i,z_i|\Theta) \] 但是,优化求解含有未观测数据Z的对数似然函数\(L(\Theta,Z)\)十分困难,EM算法不断构造对数似然函数\(L(\Theta,Z)\)的一个下界(E步骤),然后最大化这个下界(M步骤),以迭代方式逼近模型参数所能取得极大似然值
五、深度学习
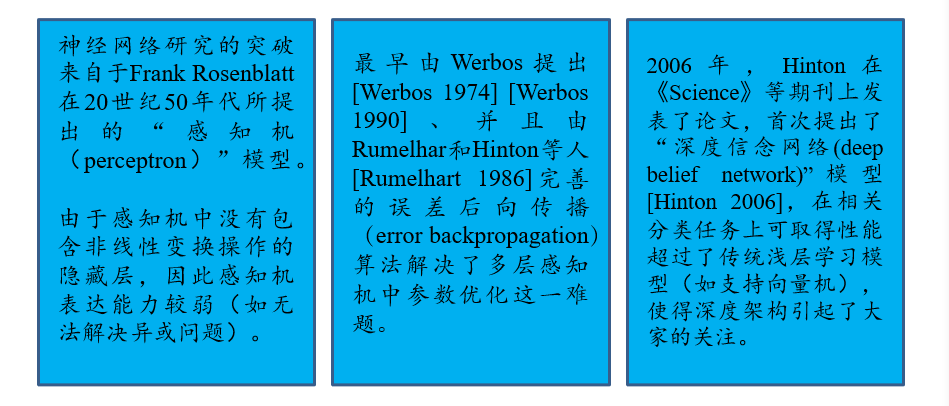
5.1 深度学习的历史发展


5.2 前馈神经网络 FNN
5.2.1 浅层学习 vs 深层学习:分段学习=>逐层端到端学习
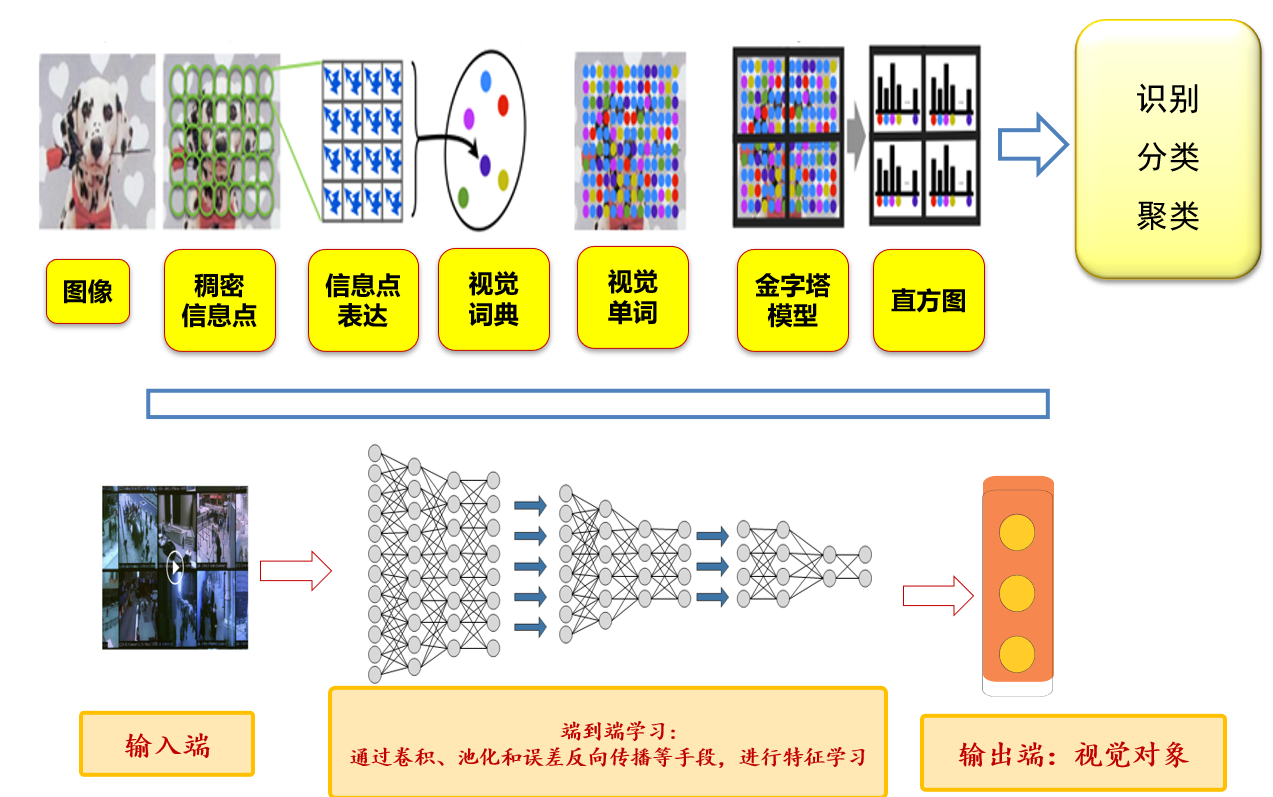
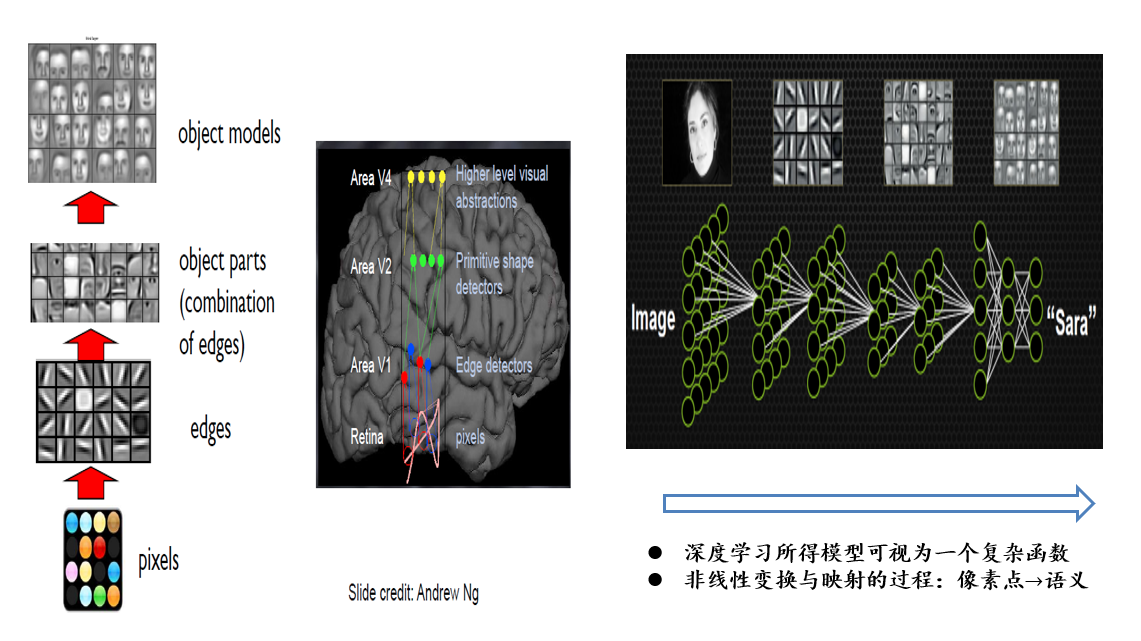
5.2.2 深度学习:以端到端的方式逐层抽象、逐层学习
- 深度学习所得的模型可以视为一个复杂函数
- 非线性变换与映射的过程:像素点→语义
5.2.3 MCP神经元
- 对n个输入数据\(x_i\)进行线性加权求和,然后利用函数\(\Phi(·)\)将结果映射为0/1
- 特点:
- 可计算、清晰描述
- 既包含了物理反应(线性加权求和),也包含了化学反应(阈值函数)
- 缺点:
- 权重\(w_i\)是人工定制的,没有通过数据驱动,没有学习的过程
- 阈值函数的阈值也是人工定制的

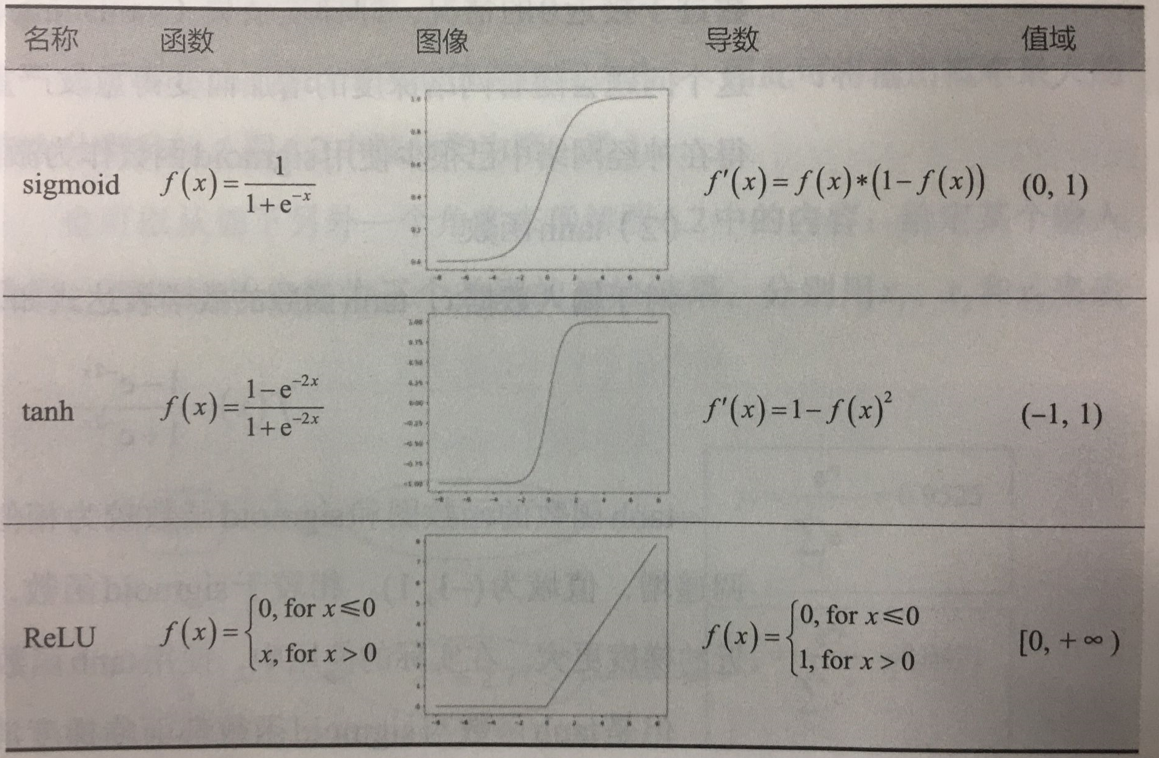
5.2.3 激活函数:对输入信息进行非线性变换
5.2.3.1 常用激活函数:sigmoid、tanh、ReLU
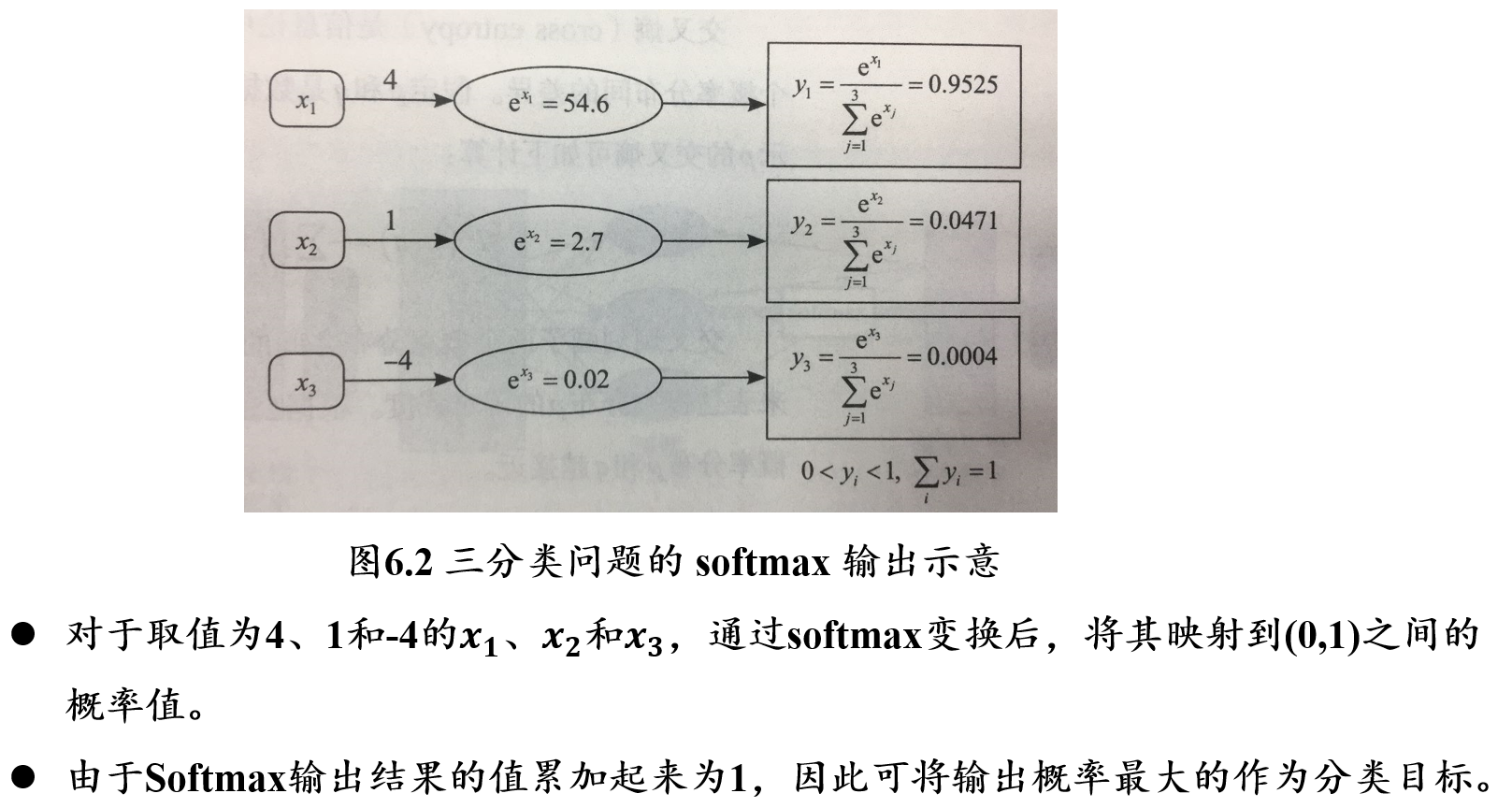
5.2.3.2 softmax函数:将输出映射到[0,1]概率空间
\[ y_i=softmax(x_i)=\frac{e^{x_i}}{\sum_{j=1}^k e^{x_j}} \]
- 将输入数据\(x_i\)映射到[0, 1]的概率空间,用于刻画每个输入的相对重要程度
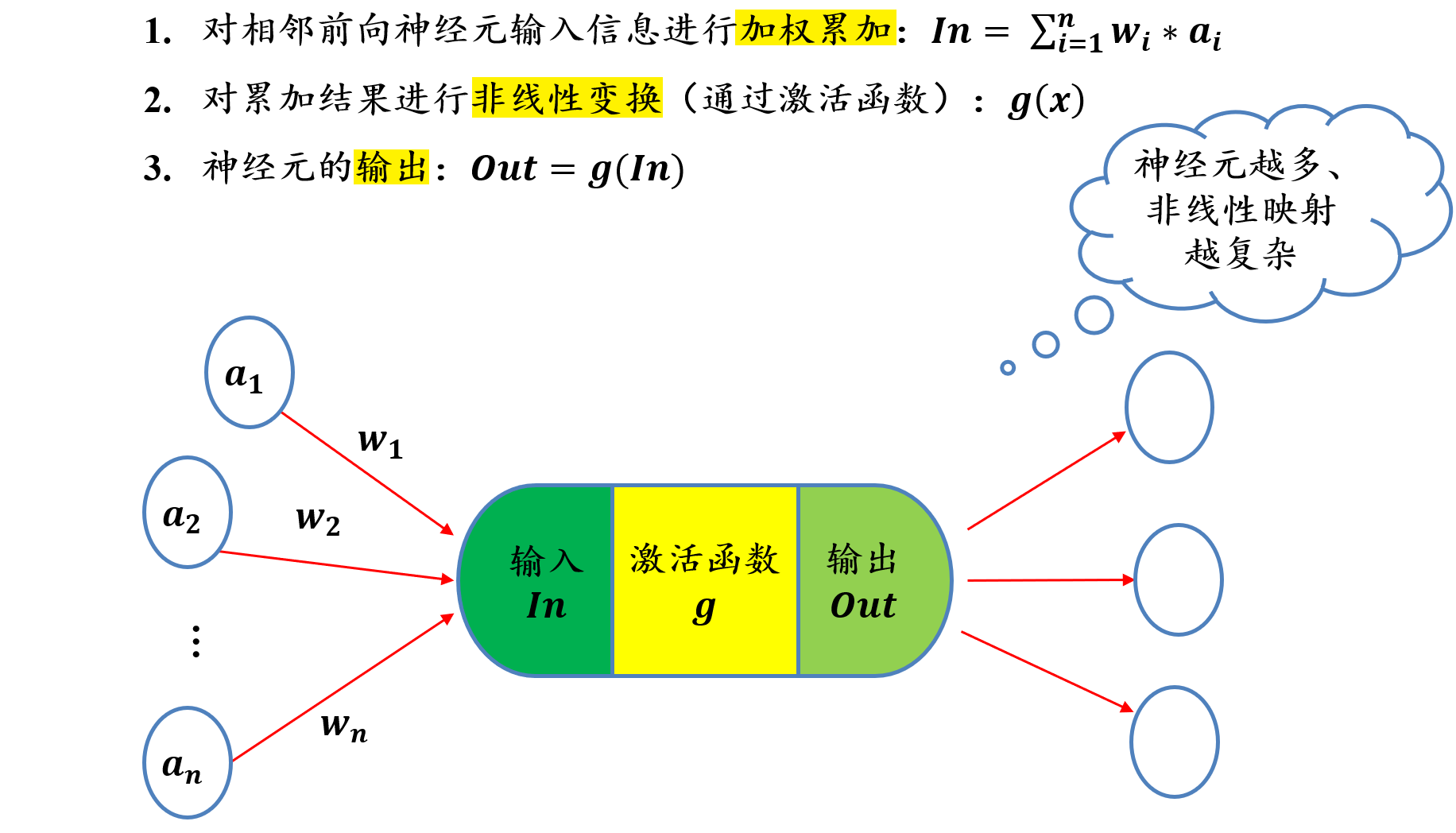
5.2.4 单个神经元的功能:加权累加 + 非线性变换
参数是学习出来的
5.2.5 损失函数 Loss Function
损失函数:又称为代价函数(Cost Function)
- 用来计算模型预测值与真实值之间的误差
- 损失函数是神经网络设计中的一个重要组成部分,通过定义与任务相关的良好损失函数,在训练过程中可根据损失函数来计算神经网络的误差大小,进而优化神经网络参数
两种最常用损失函数:
- 均方误差损失函数
- 交叉熵损失函数
5.2.5.1 均方误差损失 MSE:预测值和实际值之间的差
均方误差损失函数:
- 计算预测值和实际值之间的距离(即误差)的平方,衡量模型的优劣
- 设有n个训练数据\(x_i\),每个训练数据的真实输出为\(y_i\),模型对\(x_i\)的预测为\(\hat{y_i}\),则该模型在n个训练数据下产生的均方误差损失为:
\[ MSE=\frac{1}{n}\sum_{i=1}^n(y_i-\hat{y_i})^2 \]
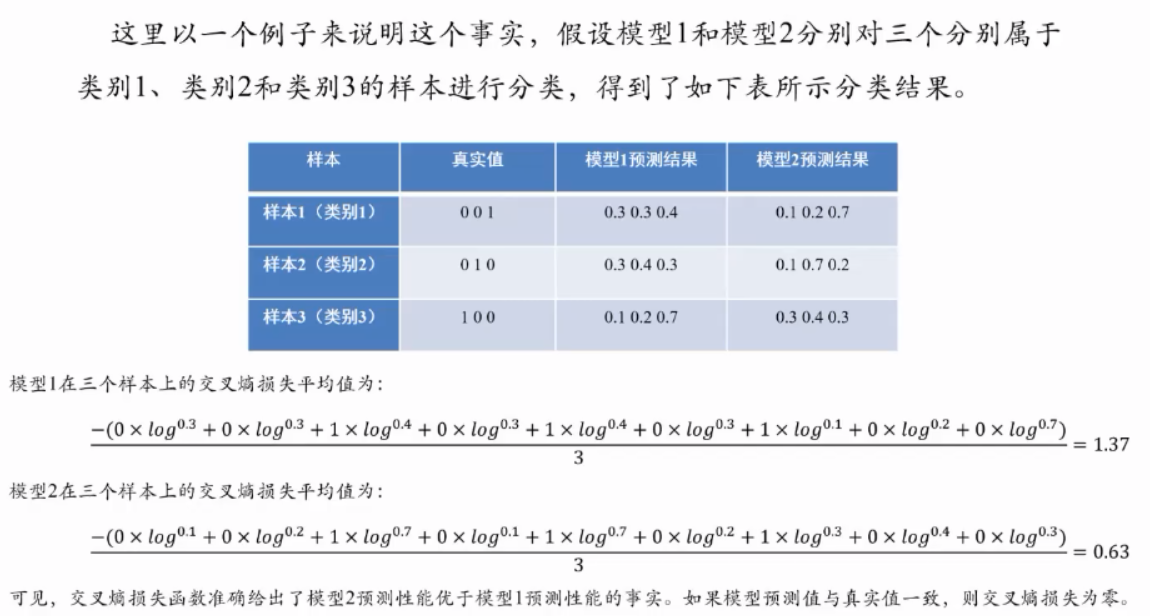
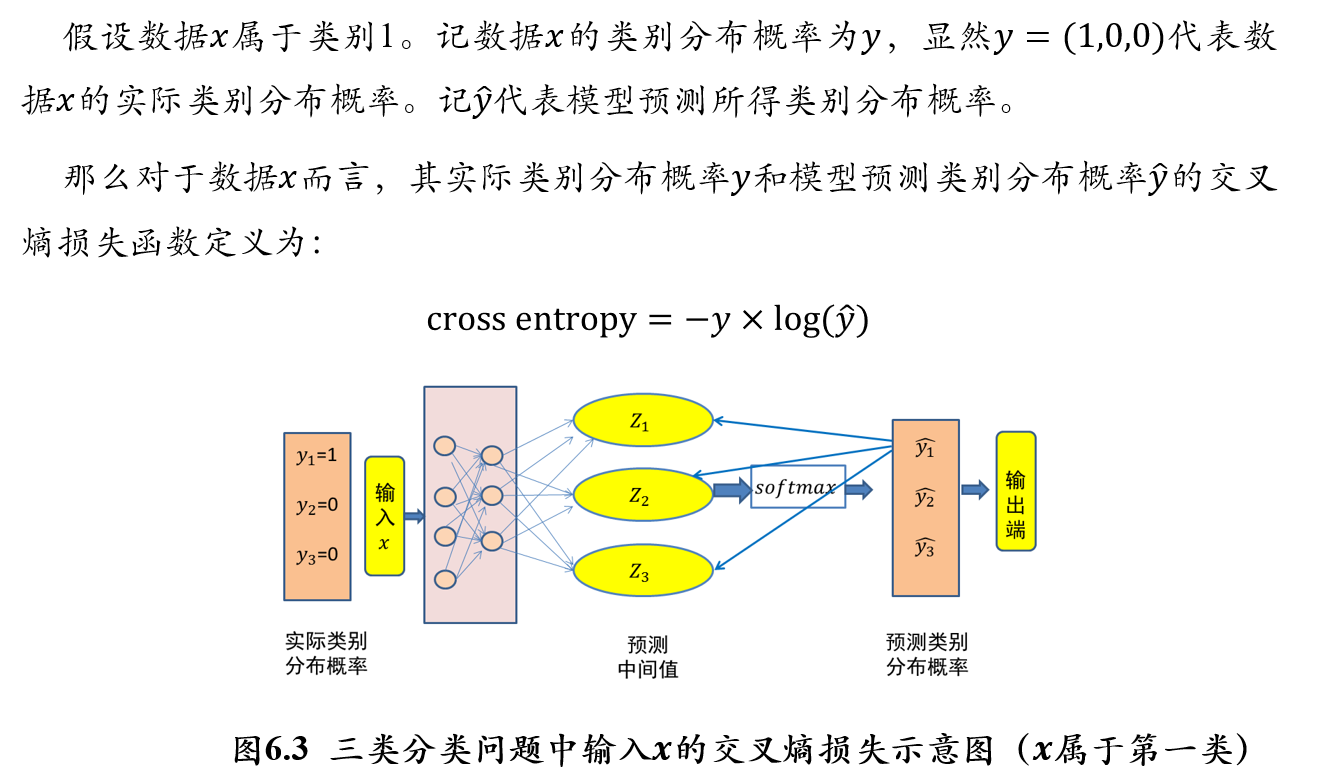
5.2.5.2 交叉熵损失函数:两个概率分布之间的距离
交叉熵(cross entropy):
- 交叉熵刻画了两个概率分布之间的距离,旨在描绘通过概率分布q来表达概率分布p的困难程度
- 交叉熵越小,两个概率分布p和q越接近
- 设p和q是数据x的两个概率分布,则通过q来表示p的交叉熵为:
\[ H(p,q)=-\sum_x p(x)*\log q(x) \]


5.2.6 感知机模型
5.2.6.1 单层感知机
- 早期的感知机结构和MCP模型相似,由一个输入层和一个输出层构成,因此也被称为“单层感知机”
- 感知机的输入层负责接收实数值的输入向量,输出层则能输出1或-1两个值
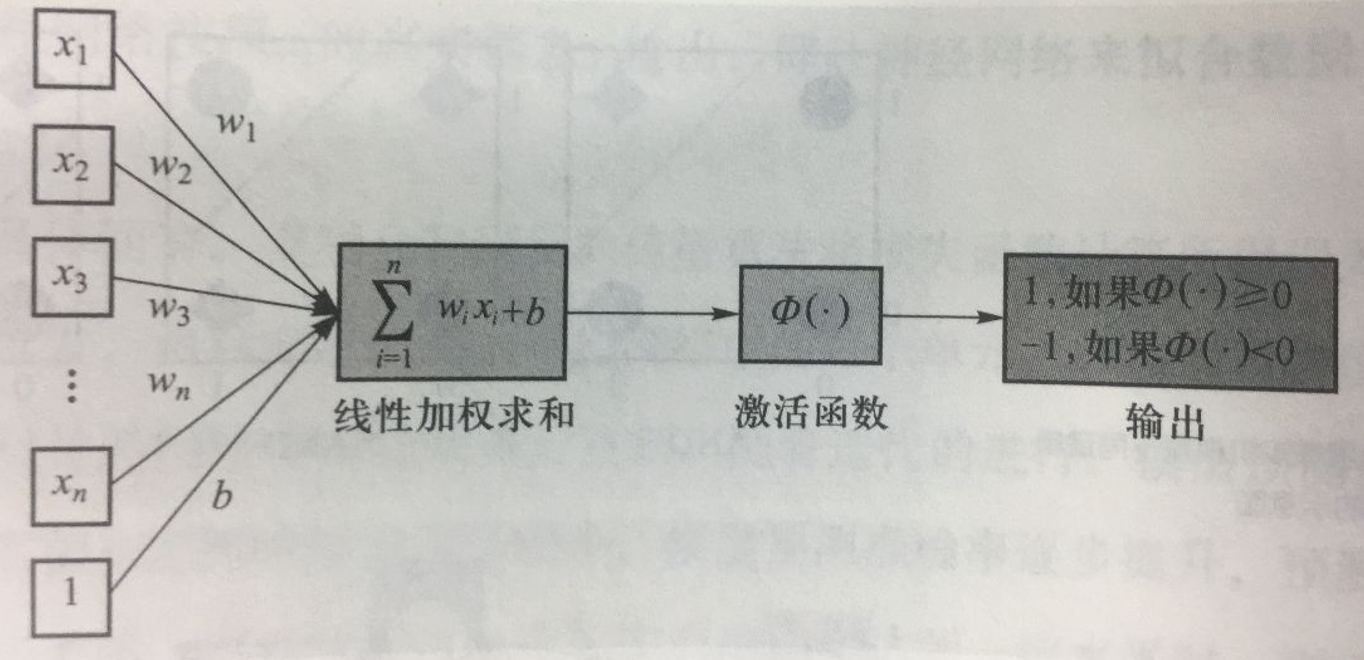
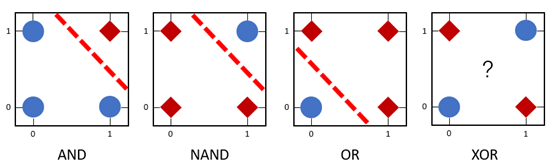
- 单层感知机可被用来区分线性可分数据
- 在下图中,AND、NAND和OR为线性可分函数,所以可利用单层感知机来模拟这些逻辑函数
- 但是,由于XOR是非线性可分的逻辑函数,因此单层感知机无法模拟逻辑异或函数的功能
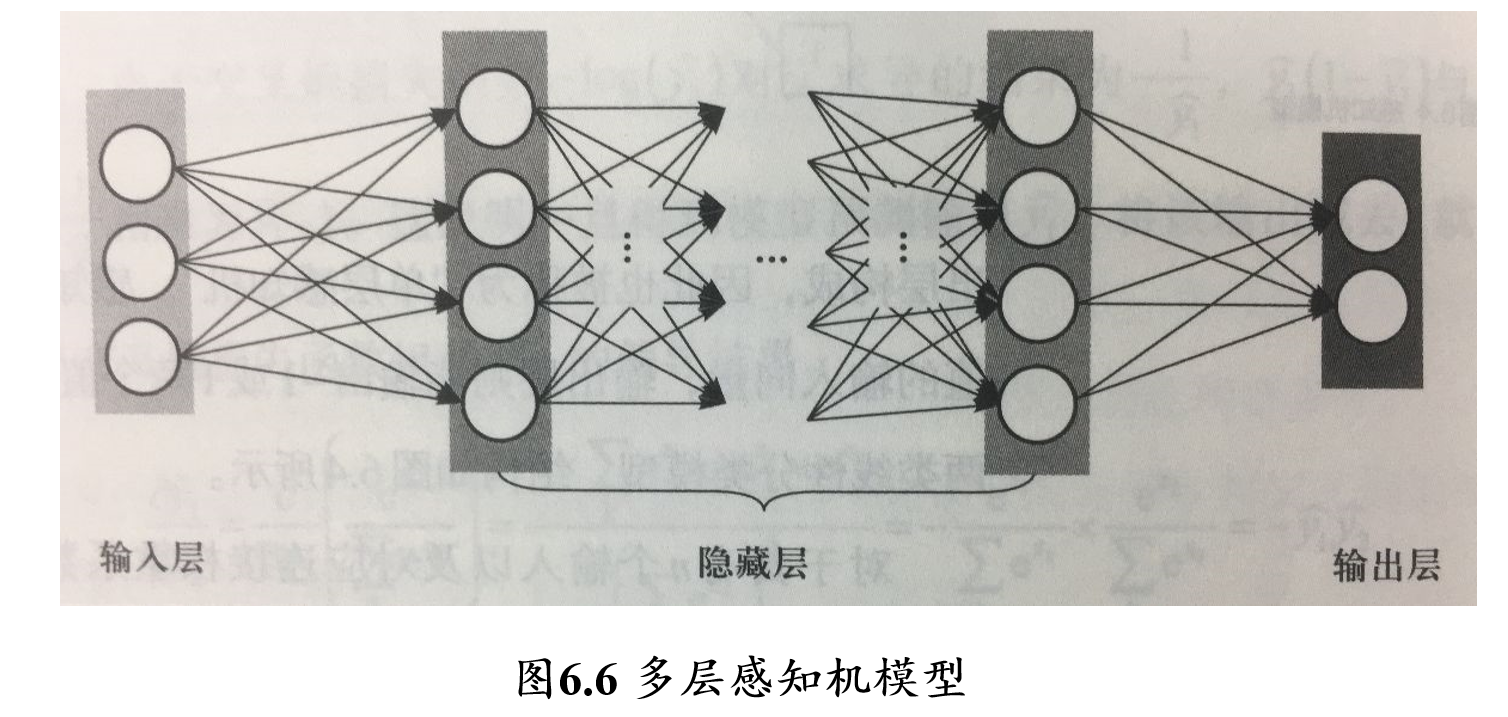
5.2.6.2 多层感知机/前馈神经网络(FNN)
多层感知机:由输入层、输出层和至少一层的隐藏层构成
- 网络中各个隐藏层中神经元可接收相邻前序隐藏层中所有神经元传递而来的信息,经过加工处理后将信息输出给相邻后续隐藏层中所有神经元
- 各个神经元接受前一级的输入,并输出到下一级,模型中没有反馈
- 层与层之间通过“全连接”进行链接,即两个相邻层之间的神经元完全成对连接,但层内的神经元不相互连接
- 前馈神经网络 feedforward neural network
5.2.7 参数优化
目标:最小化损失函数
5.2.7.1 梯度下降 Gradient Descent
梯度:
一元变量所构成的函数\(f\)在\(x\)处的梯度为: \[ \frac{df(x)}{dx}=\lim_{h→0} \frac{f(x+h)-f(x)}{h} \]
在多元函数中,梯度是对每一变量所求导数组成的向量
梯度的反方向是函数值下降最快的方向,因此是损失函数求解的方向
在实际中,引入步长η(为定值),用\(x-η𝜵f(x)\)来更新\(x\)

证明过程:
设损失函数\(f(x)\)是连续可微的多元变量函数,其泰勒展开为: \[ f(x+Δx) = f(x) + f'(x)Δx + \frac{1}{2}f''(x)(Δx)^2+...+\frac{1}{n!}f^{(n)}(Δx)^n\\ f(x+Δx) - f(x) ≈ (𝜵f(x))^TΔx \]
因为我们的目的是最小化损失函数\(f(x)\),则\(f(x+Δx) < f(x)\),即\((𝜵f(x))^TΔx<0\)
在\((𝜵f(x))^TΔx = |𝜵f(x)||Δx|cosθ\)中,\(|𝜵f(x)|\)为损失函数梯度的模,\(|Δx|\)为下一轮迭代中x取值增量的模,两者均为正数。为了保证损失误差减少,只要保证\(cos θ<0\)
当\(θ = 180°\)时,\(cos θ=-1\),此时损失函数减少的幅度值\((𝜵f(x))^TΔx\)取到最小值
因此\(Δx\)的选取应该为\(𝜵f(x)\)的反方向
5.2.7.2 误差反向传播 BP
Error Back Propagation
- BP算法是一种将输出层误差反向传播给隐藏层进行参数更新的方法
- 将误差从后向前传递,将误差分摊给各层所有单元,从而获得各层单元所产生的误差,进而依据这个误差来让各层单元负起各自责任、修正各单元参数
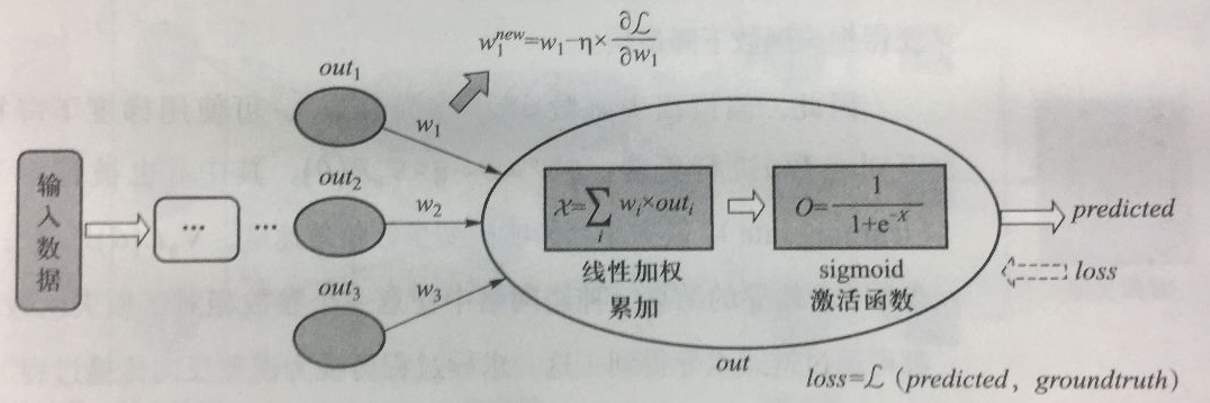
- 每个参数经过误差反向传播后,新的参数值为:
\[ \begin{aligned} w^{new} &= w_1-η×\frac{\partial{\mathcal{L}}}{\partial{w_1}}\\ &= w_1-η×\frac{d\mathcal{L}}{d\mathcal{O}}×\frac{d\mathcal{O}}{d\mathcal{X}}×\frac{d\mathcal{X}}{d\mathcal{w_1}}\\ &= w_1-η×\frac{d\mathcal{L}}{d\mathcal{O}}×\frac{1}{1+e^{-x}}×(1-\frac{1}{1+e^{-x}})×out_1 \end{aligned} \]
5.2.7.3 链式求导法则
- 由于\(w_1\)与加权累加函数\(\mathcal{X}\)和sigmoid函数均有关,因此\(\frac{d\mathcal{L}}{dw_1}=\frac{d\mathcal{L}}{d\mathcal{O}}·\frac{d\mathcal{O}}{d\mathcal{X}}·\frac{d\mathcal{X}}{d\mathcal{w_1}}\)
- 在这个链式求导中:
- \(\frac{d\mathcal{L}}{d\mathcal{O}}\):与损失函数的定义有关
- \(\frac{d\mathcal{O}}{d\mathcal{X}}\):是对sigmoid函数求导,结果为\(\frac{1}{1+e^{-x}}·(1-\frac{1}{1+e^{-x}})\)
- \(\frac{d\mathcal{X}}{dw_1}\):是加权累加函数\(\sum_{i=1}^n w_i·out_i\),结果为\(out_i\)
- 链式求导实现了损失函数对某个自变量求偏导,好比将损失误差从输出端向输入端逐层传播,通过这个传播过程来更新该自变量取值。梯度下降法告诉我们,只要沿着损失函数梯度的反方向来更新参数,就可使得损失函数下降最快
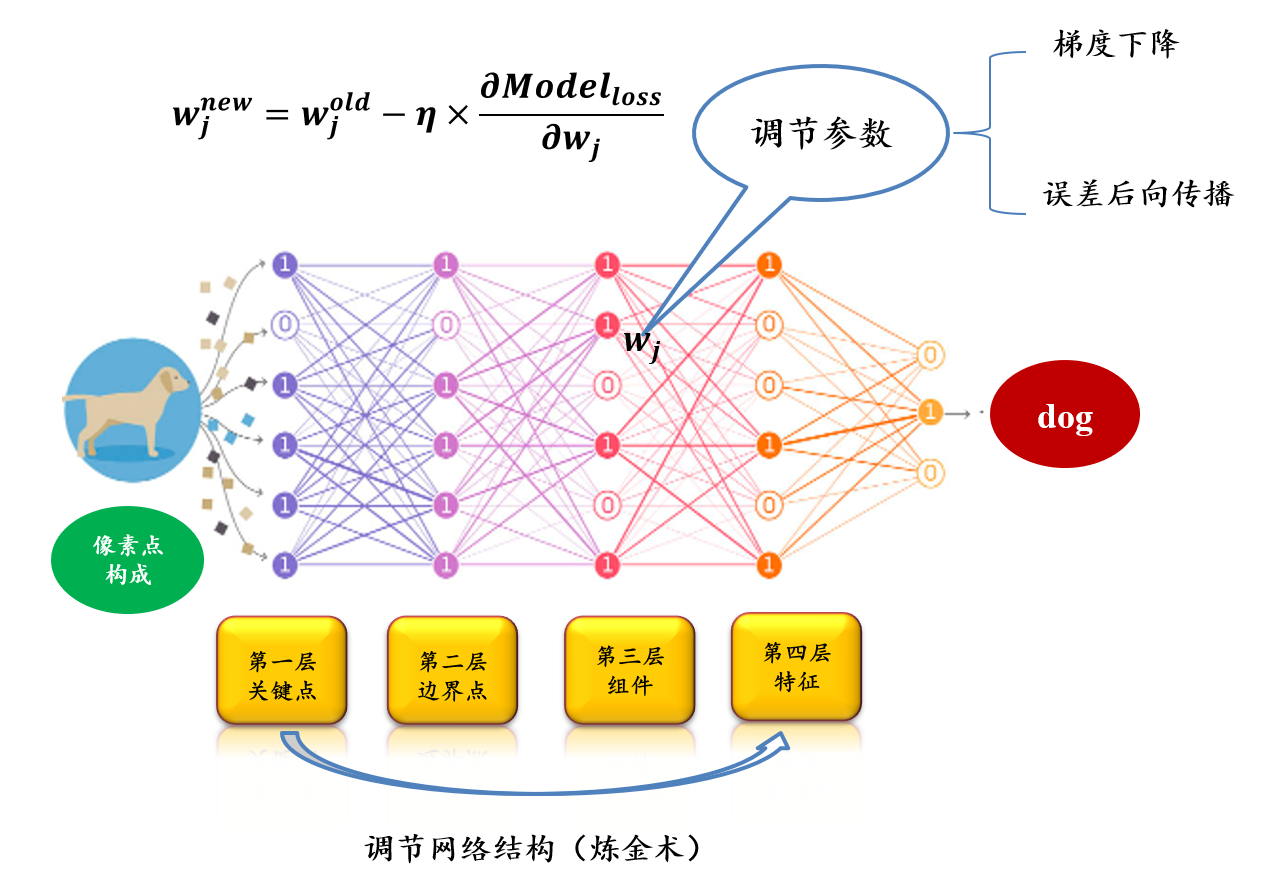
5.2.8 机器学习的能力在于拟合和优化
5.3 卷积神经网络 CNN
convolution neural network
CNN引入了一个卷积层,将原始图像先经过一次卷积(即下采样),然后再送入FNN进行学习
- CNN = 卷积层 + 池化层 + 全连接层 + Softmax激活函数
5.3.1 卷积操作:线性操作
5.3.1.1 卷积核的权重是通过学习得出的
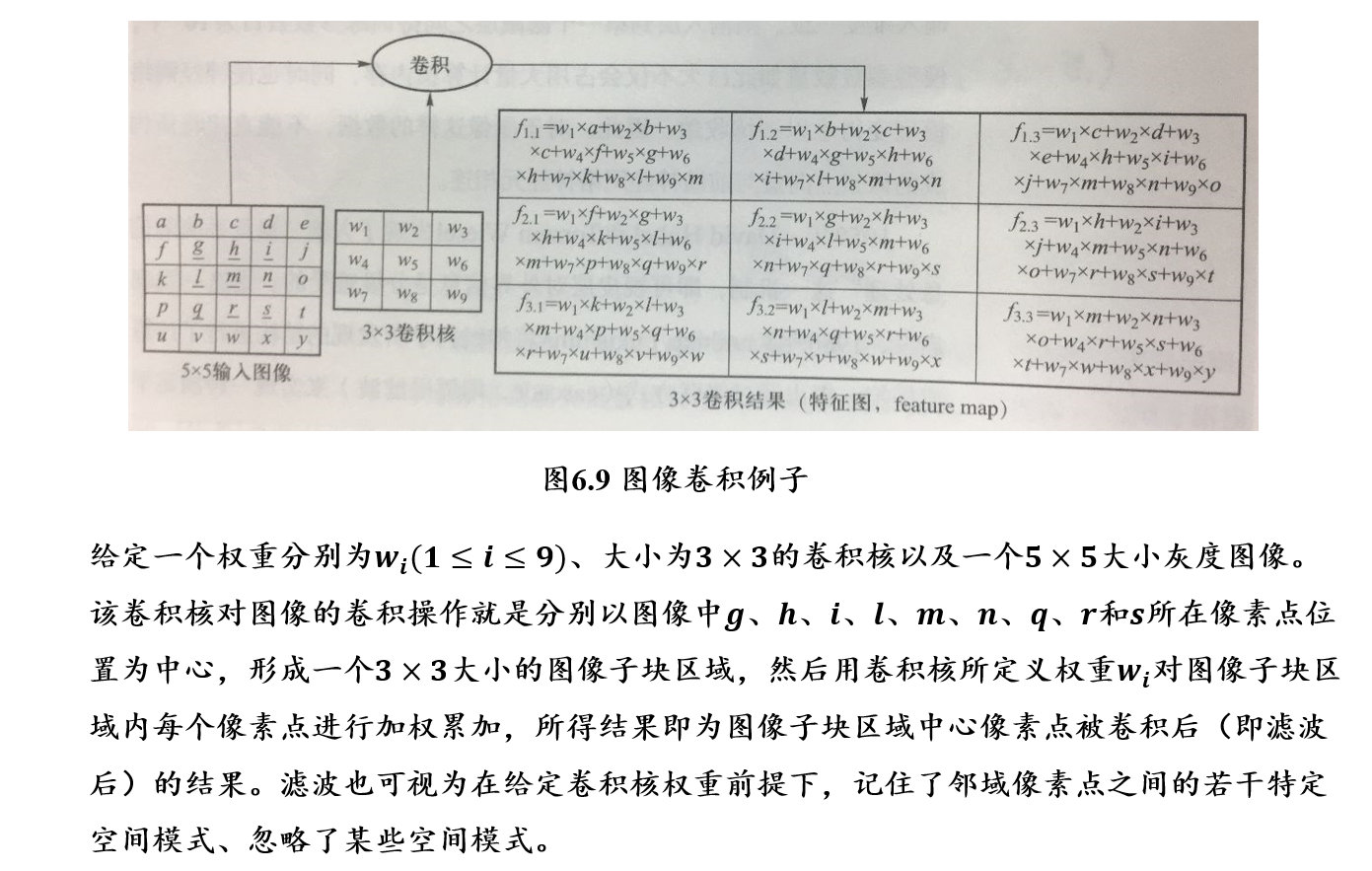
- 图像中像素点具有很强的空间依赖性,卷积就是针对像素点的空间依赖性来对图像进行处理的一种技术
- 在图像卷积计算中,需要定义一个卷积核(kernel)
- 卷积核是一个二维矩阵
- 矩阵中数值为对图像中与卷积核同样大小的子块像素点进行卷积计算时所采用的权重
- 卷积核中的权重系数wi是通过数据驱动机制学习得到,其用来捕获图像中某像素点及其邻域像素点所构成的特有空间模式
- 一旦从数据中学习得到权重系数,这些权重系数就刻画了图像中像素点构成的空间分布不同模式
5.3.1.2 对图像进行卷积操作
- 如果卷积核中心位置的权重系数越小且与其它卷积权重系数差别越小,则卷积所得到图像滤波结果越模糊,这被称为图像平滑操作
- 7×7大小的图像,通过3×3大小卷积核以1的步长进行卷积操作,可得到5×5大小的卷积结果
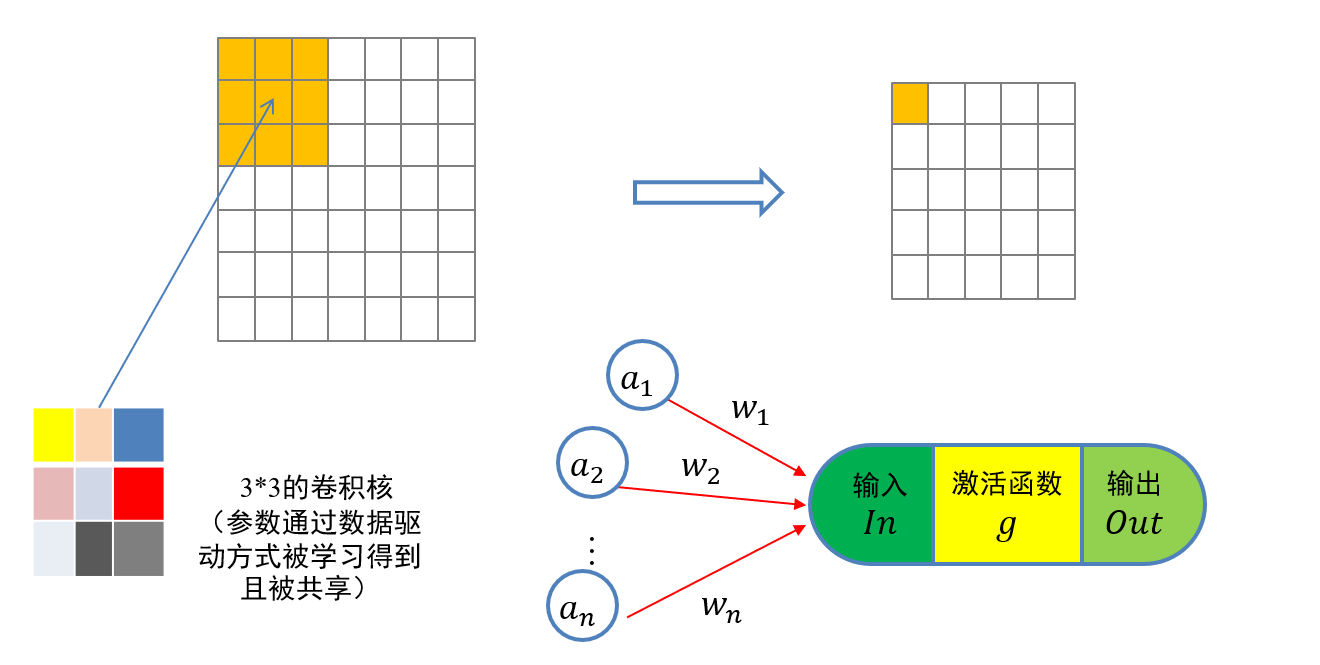
5.3.1.3 卷积核、特征图、感受野

5.3.2 池化操作:非线性操作
- 进一步进行下采样操作
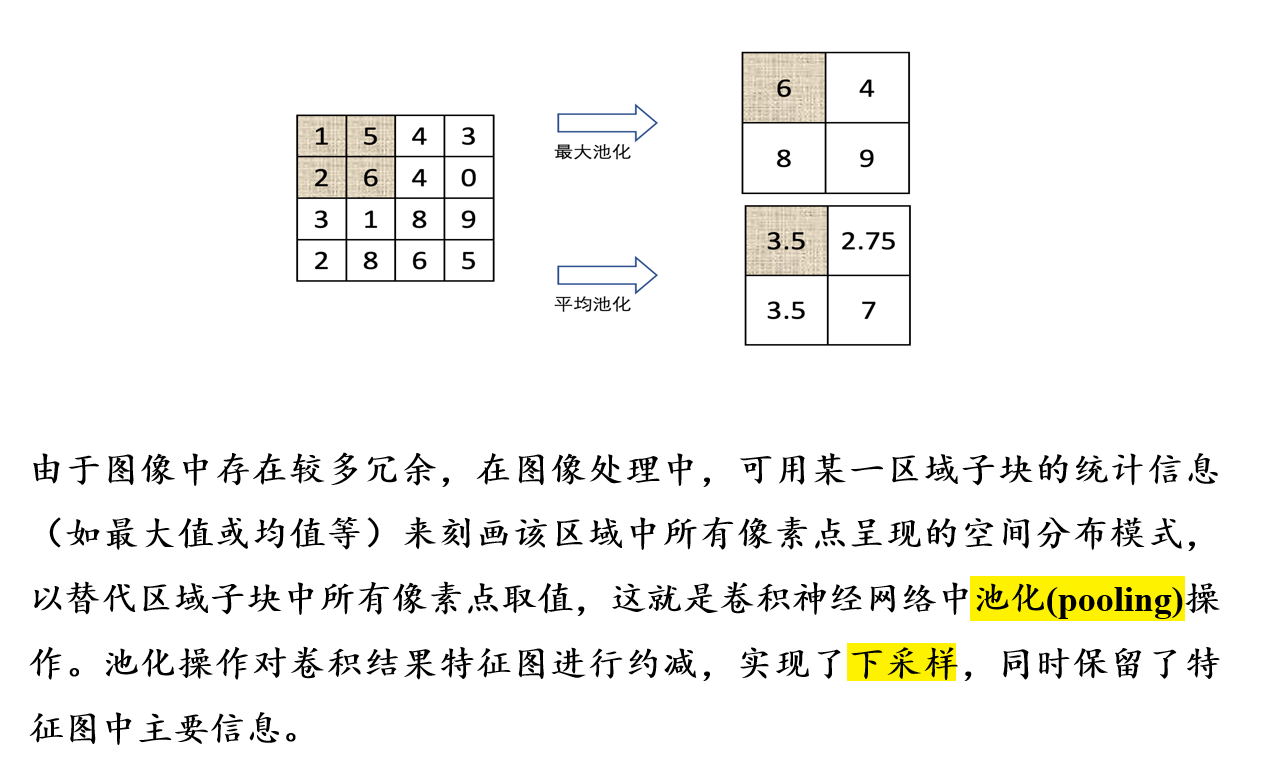
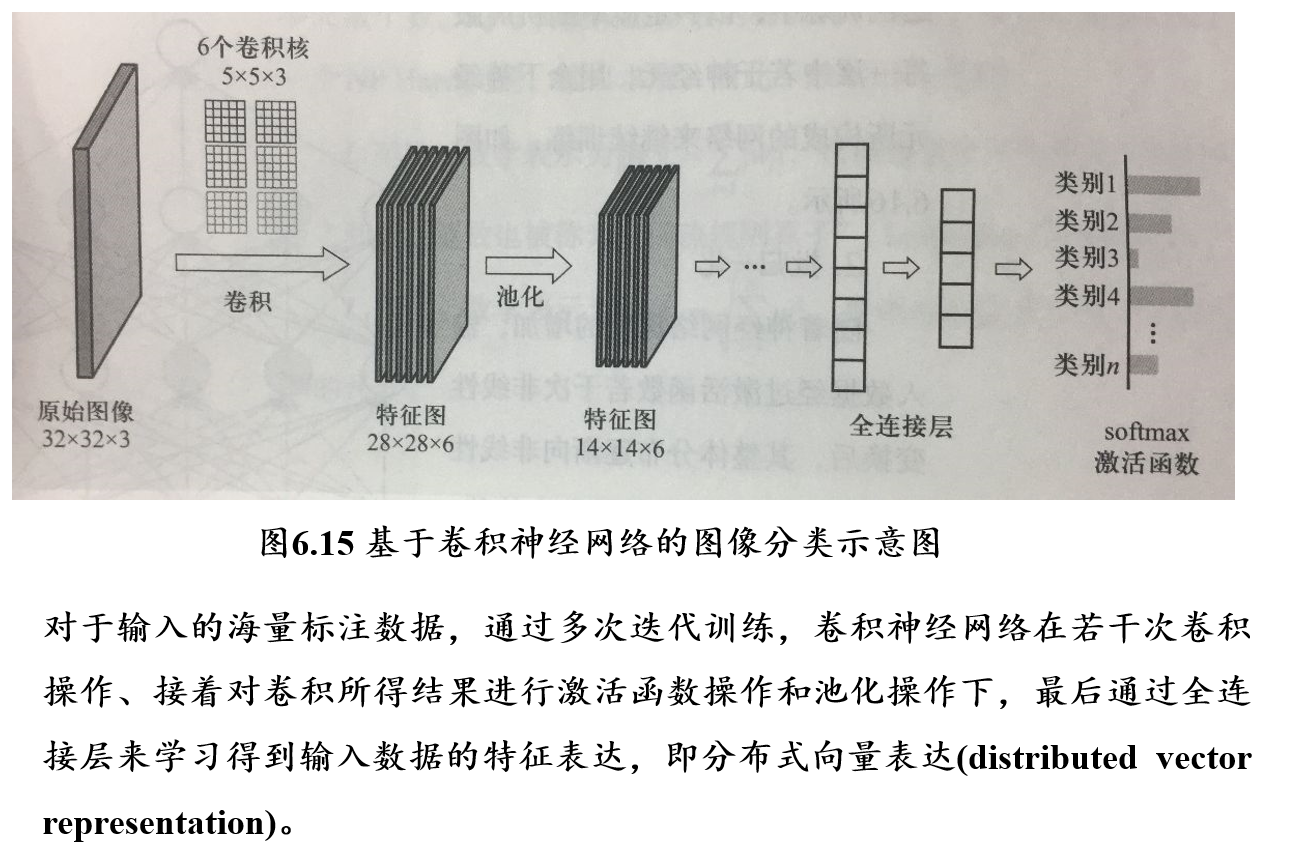
5.3.3 神经网络正则化:解决过拟合问题
为了缓解神经网络在训练过程中出现的过拟合问题,需要采取一些正则化技术来提升神经网络的泛化能力(generalization)
Dropout:随机删除一定比例的连接
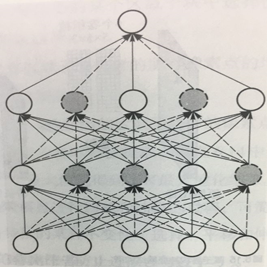
Batch-Normalization:一次送入一批图像,而不是一张图像,一批图像之间有一定的关联度
L1-Norm & L2-Norm:

5.4 循环神经网络 RNN
循环神经网络:处理序列数据时所采用的网络结构
- 先前所介绍的前馈神经网络或卷积神经网络所需要处理的输入数据一次性给定,难以处理存在前后依赖关系的数据
- 循环神经网络的本质是希望模拟人所具有的记忆能力,在学习过程中记住部分已经出现的信息,并利用所记住的信息影响后续结点输出
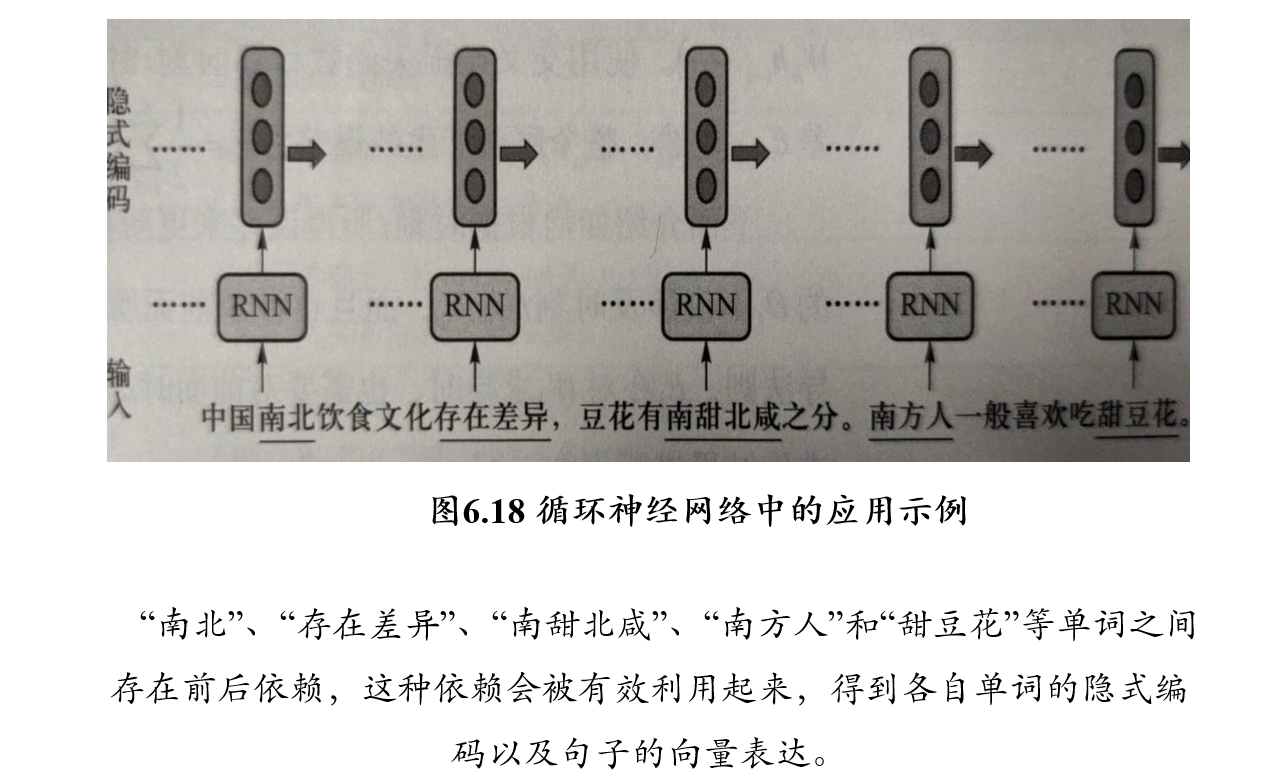
- 循环神经网络在自然语言处理,例如语音识别、情感分析、机器翻译等领域有重要应用
5.4.1 RNN的结构
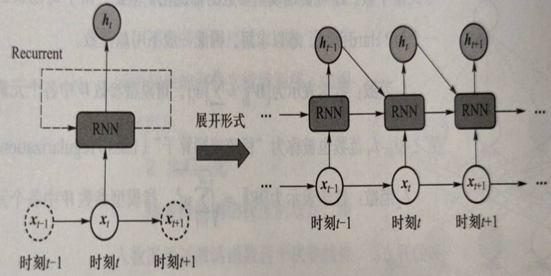
循环神经网络在处理数据过程中构成了一个循环体
- 对于一个序列数据,在每一时刻\(t\),循环神经网络单元会读取当前输入数据\(x_t\)和前一时刻输入数据\(x_{t−1}\)所对应的隐式编码结果\(h_{t−1}\),一同生成\(t\)时刻的隐式编码结果\(h_t\)
- 接着将\(h_t\)后传,去参与生成\(t+1\)时刻输入数据\(x_{t+1}\)的隐式编码\(h_{t+1}\)
时刻\(t\)所得到的隐式编码\(h_t\)是由上一时刻隐式编码\(h_{t-1}\)和当前输入\(x_t\)共同参与生成的
- 这可认为隐式编码\(h_{t-1}\)已经“记忆”了\(t\)时刻之前的时序信息,或者说前序时刻信息影响了后续时刻信息的处理
- 与前馈神经网络和卷积神经网络在处理时需要将所有数据一次性输入不同,这体现了循环神经网络可刻画序列数据存在时序依赖这一重要特点
在时刻\(t\),一旦得到当前输入数据\(x_t\),RNN会结合前一时刻的隐式编码\(h_{t-1}\),生成当前时刻的隐式编码\(h_t\): \[ \begin{aligned} h_t &= \Phi(U×x_t+W×h_{t-1}) \\ &= \Phi(U×x_t+W×\Phi(U×x_{t-1}+W×h_{t-2})) \\ &= \Phi(U×x_t+W×\Phi(U×x_{t-1}+W×\Phi(U×x_{t-2}+...)))) \end{aligned} \]
- \(\Phi(·)\):激活函数,一般为Sigmoid或Tanh,使模型能够忘掉一些信息,同时更新记忆内容
- \(U、W\):模型参数,对于每一时刻都是共用的
5.4.2 沿时间反向传播算法 BPTT
Back Propagation Through Time
5.4.2.1 思想
- 按照时间将RNN展开后,可以得到一个和FNN相似的网络结构
- 这个网络结构可以利用BP和Gradient Descent算法来训练模型参数,这种训练方法被称为BPTT
- 由于RNN每一时刻都有一个输出,因此在计算RNN的损失时,需要将所有时刻上的损失进行累加
5.4.2.2 算法
设时刻\(t\)隐式编码如下得到: \[ h_t=tanh(W_xt_x+W_hh_{t-1}+b) \]
使用交叉熵损失函数计算时刻\(t\)预测输出与实际输出的误差为\(E_t\),则整个序列产生的误差为: \[ E=\frac{1}{2}\sum_{t=1}^T E_t \]
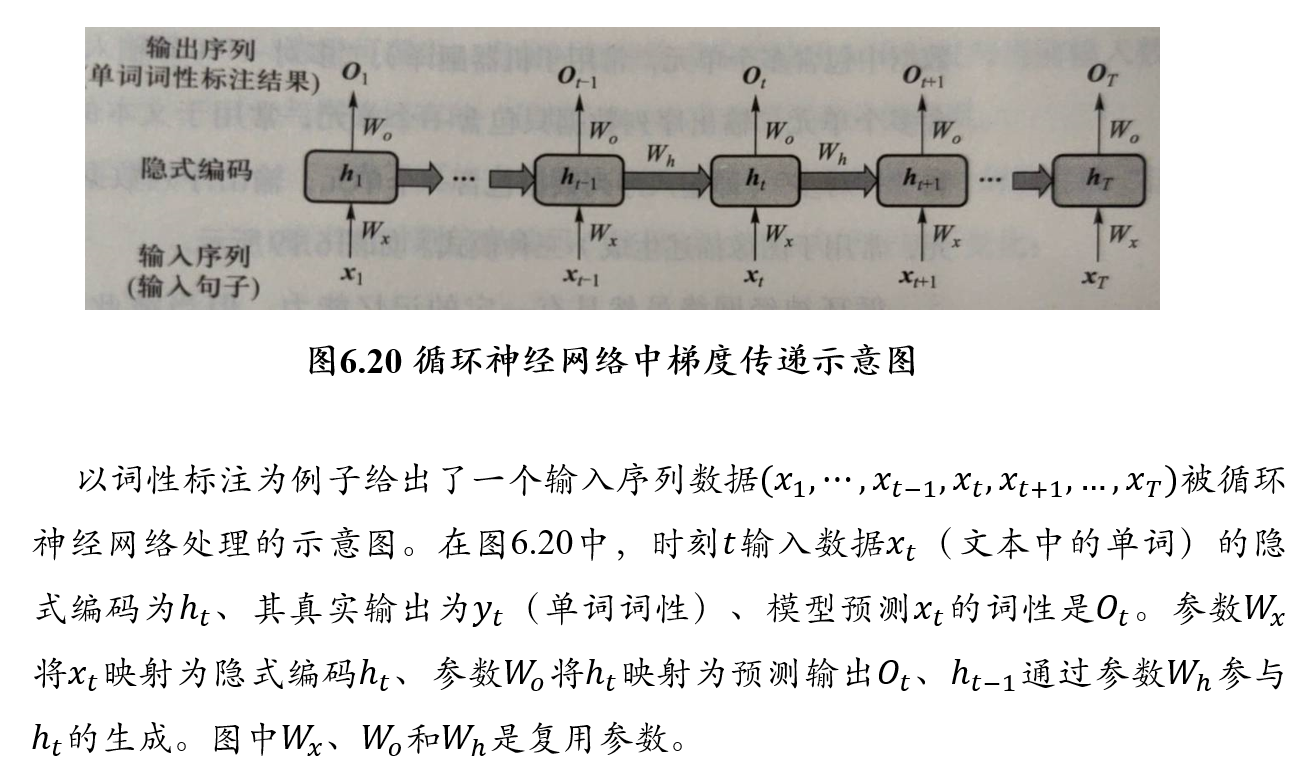
根据时刻\(t\)所得到的误差来更新参数\(W_x\)的方法为:
- 在时刻\(t\)计算所得的\(O_t\)不仅涉及到了\(t\)时刻的\(W_x\),而且也涉及了前面所有时刻的\(W_x\)
- 按照链式求导法则,\(E_t\)对\(W_x\)求导时,也需要对前面时刻的\(W_x\)依次求导,然后再将求导结构进行累加,即:
\[ \frac{\partial E_t}{\partial W_x}=\sum_{i=1}^y \frac{dE_t}{dO_t}·\frac{dO_t}{dh_t}·(\prod_{j=i+1}^t \frac{dh_j}{dh_{j-1}})·\frac{dh_i}{dW_x}\\ 其中, \prod_{j=i+1}^t \frac{dh_j}{dh_{j-1}}=\prod_{j=i+1}^t tanh'×W_h \]
令\(t=3\),则有: \[ \begin{aligned} \frac{\partial E_3}{\partial W_x}&=\frac{dE_3}{dO_3}·\frac{dO_3}{dh_3}·\frac{dh_3}{dW_x}\\ &+\frac{dE_3}{dO_3}·\frac{dO_3}{dh_3}·\frac{dh_3}{dh_2}·\frac{dh_2}{dW_x}\\ &+\frac{dE_3}{dO_3}·\frac{dO_3}{dh_3}·\frac{dh_3}{dh_2}·\frac{dh_2}{dh_1}·\frac{dh_1}{dW_x} \end{aligned} \]
由于tanh函数的导数取值位于[0,1]区间,对于长序列而言,若干个[0,1]区间的小数相乘,会使得参数求导结果很小,引发梯度消失问题。\(E_t\)对\(W_h\)的求导类似。
为了解决梯度消失问题,提出了长短时记忆模型(LSTM)
5.4.2.3 应用
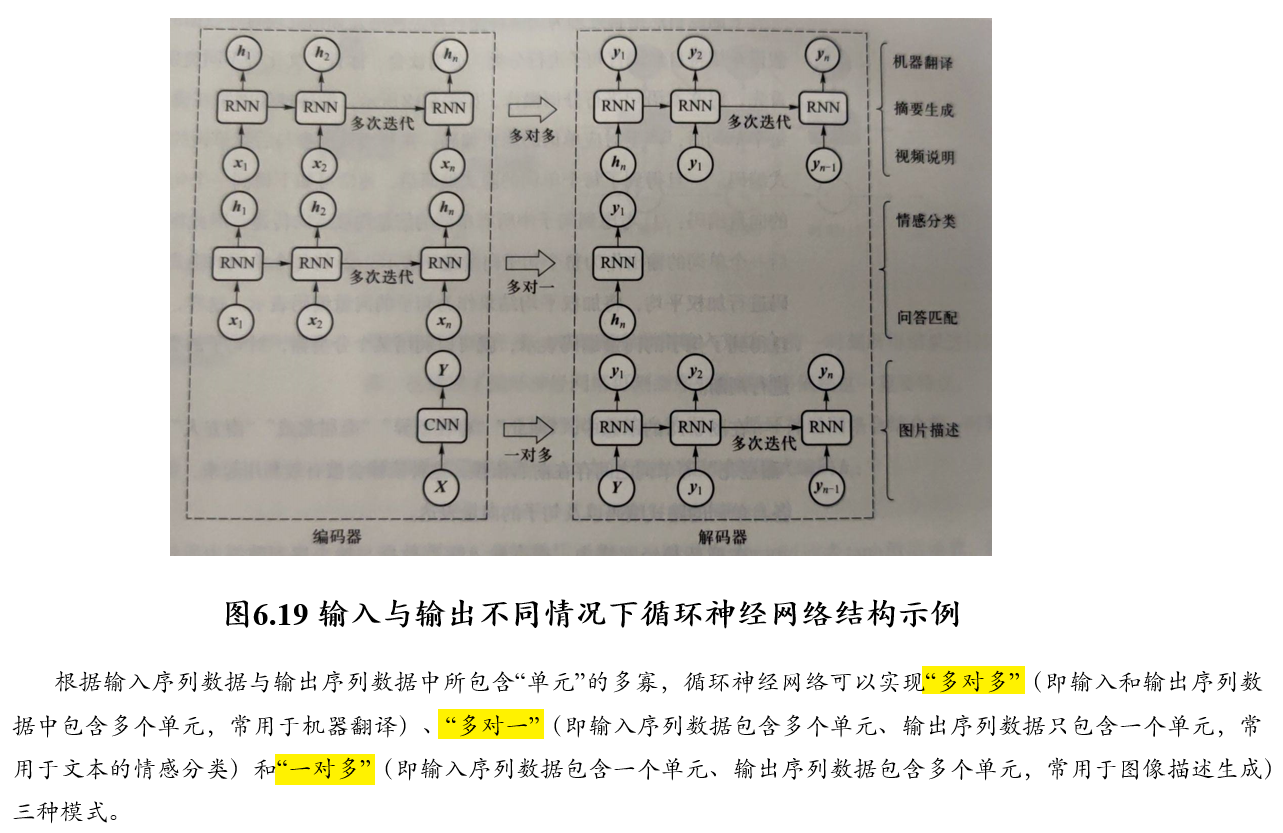
5.4.3 长短时记忆模型 LSTM:解决RNN梯度消失的问题
Long-Short-Term-Memory
5.4.3.1 思想
LSTM网络中引入了内部记忆单元(internal memory cell)和门(gates)两种结构来对当前时刻输入信息以及前序时刻所生成信息进行整合和传递
- 在这里,内部记忆单元中信息可视为对“历史信息”的累积
- 常见的LSTM模型中有输入门(input gate)、遗忘门(forget gate)和输出门(output gate)三种门结构
- 对于给定的当前时刻输入数据\(x_t\)和前一时刻隐式编码\(h_{t-1}\),输入门、遗忘门和输出门通过各自参数对其编码,分别得到三种门结构的输出\(i_t, f_t, o_t\)
- 在此基础上,再进一步结合前一时刻内部记忆单元信息\(c_{t-1}\)来更新当前时刻内部记忆单元信息\(c_t\),最终得到当前时刻的隐式编码\(h_t\)
- \(h_t\)对应短期记忆,\(c_t\)对应长期记忆
- RNN直接传递短期记忆,因此容易遗忘
- 而LSTM通过门的作用,将短期记忆转化为长期记忆,因此记忆能力更强
5.4.3.2 符号定义
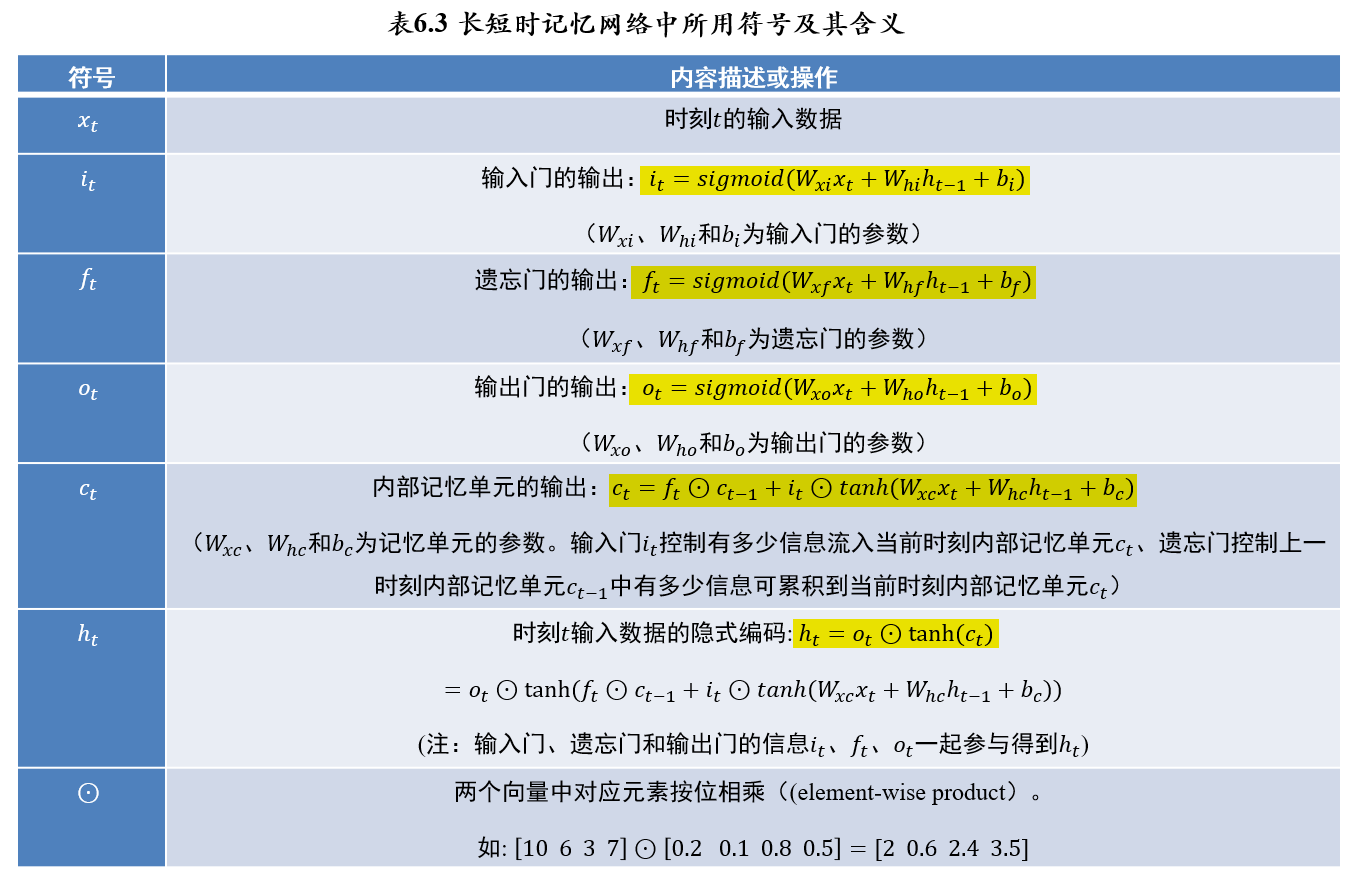
- 输入门、遗忘门和输出门通过各自参数对当前时刻输入数据\(x_𝑡\)和前一时刻隐式编码\(h_{t-1}\)处理后,利用\(𝑠𝑖𝑔𝑚𝑜𝑖𝑑\)对处理结果进行非线性映射,因此三种门结构的输出\(i_t,f_t,o_t \in(0,1)\)
- 正是由于三个门结构的输出值为位于0到1之间的向量,因此其在信息处理中起到了“调控开关”的“门”作用
- 三个门结构所输出向量的维数、内部记忆单元的维数和隐式编码的维数均相等
5.4.3.3 LSTM结构
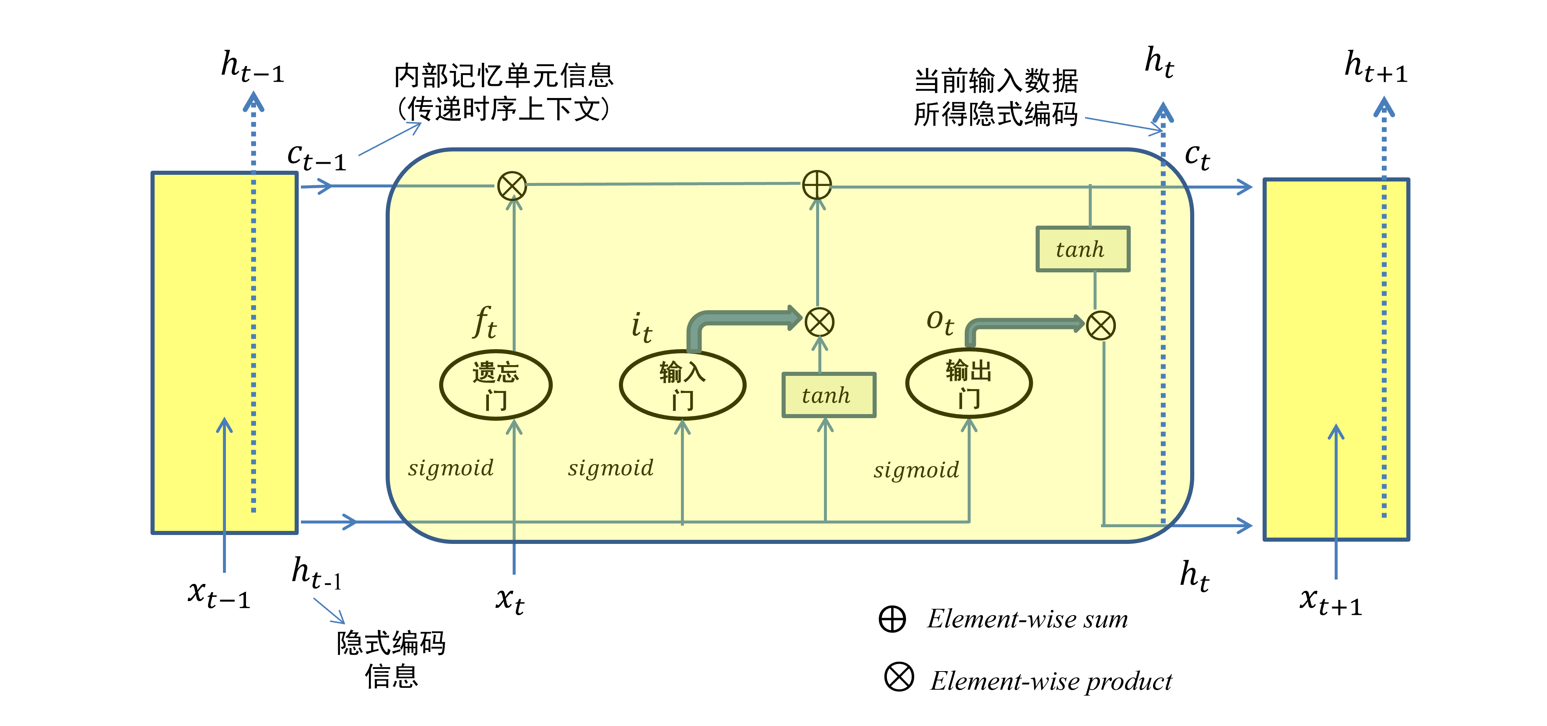
- 在每个时刻\(t\)
- 包含序列信息的变量为:\(c_t,h_t\)
- 输出为\(t\)时刻的隐式编码:\(h_t=o_t⊙tanh(c_t)\)
- LSTM中的参数有:
- 输入门\(i_t\)的参数: \(W_{xi},W_{hi},b_i → i_t=sigmoid(W_{xi}x_t+W_{hi}h_{t-1}+b_i)\)
- 遗忘门\(f_t\)的参数: \(W_{xf},W_{hf},b_f→ f_t=sigmoid(W_{xf}x_t+W_{hf}h_{t-1}+b_f)\)
- 输出门\(o_t\)的参数: \(W_{xo},W_{ho},b_o→ o_t=sigmoid(W_{xo}x_t+W_{ho}h_{t-1}+b_o)\)
- 内部记忆单元\(c_t\)的参数:\(W_{xc},W_{hc},b_c\)
- 从\(c_t=f_t⊙c_{t-1}+i_t⊙tanh(W_{xc}x_t+W_{hc}h_{t-1}+b_c)\)可以得出,对于当前时刻\(t\)所对应内部记忆单元种信息的调整,涉及到:
- 遗忘门信息\(f_t\)
- \(t-1\)时刻所对应内部记忆单元中的信息\(c_{t-1}\)
- 输入门信息\(i_t\)
- \(t-1\)时刻的隐式编码\(h_{t-1}\)
- \(sigmoid(x)\in(0,1)\):因此输入门、输出门、遗忘门三种门结构起到了信息控制门的作用
- \(tanh(x)\in(-1,1)\):因此内部记忆单元\(c_t\)、隐式编码\(h_t\)在进行信息整合时,可以起到信息增(为正)或信息减(为负)的效果
5.4.3.4 LSTM如何克服梯度消失

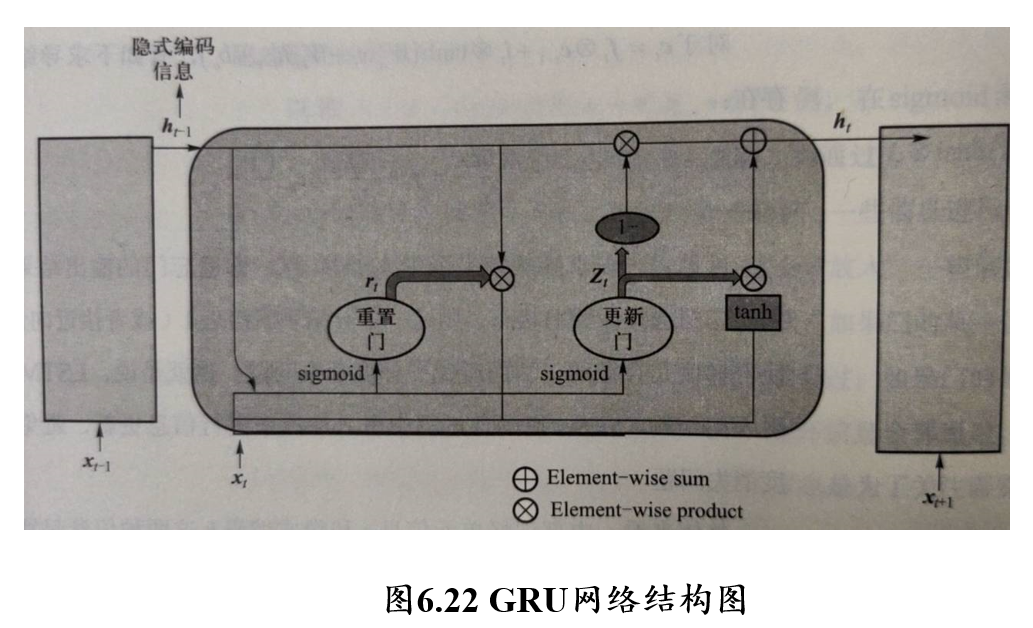
5.4.4 GRU门控循环单元神经网络
与LSTM类似,引入门结构解决梯度消失问题
(不考)5.5 深度生成学习
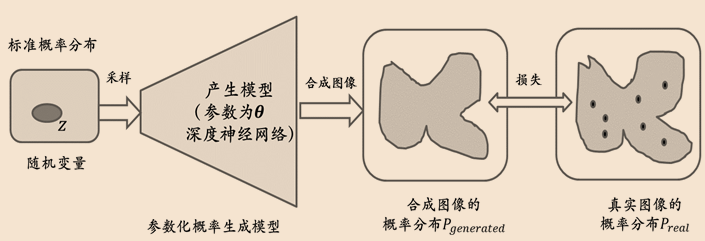
- 在本章之前的介绍中,神经网络模型从数据中提取出高层语义在数据中所蕴含的“模式”,并利用这些模式实现对数据的分类和检测等,这种模型通常称为判别模型:判别模型不关心数据如何生成,它只关心数据蕴含哪些模式以及如何将数据进行分类
- 与之相对的模型类型被称为生成模型(generative model):生成模型需要学习目标数据的分布规律,以合成属于目标数据空间的新数据
- 生成模型代表:
- 变分自编码器(variational auto-encoder, VAE)
- 自回归模型(Autoregressive models)
- 生成对抗网络(generative adversarial network,GAN)
5.6 深度学习应用
5.6.1 自然语言中词向量生成


5.6.2 Word2Vec模型
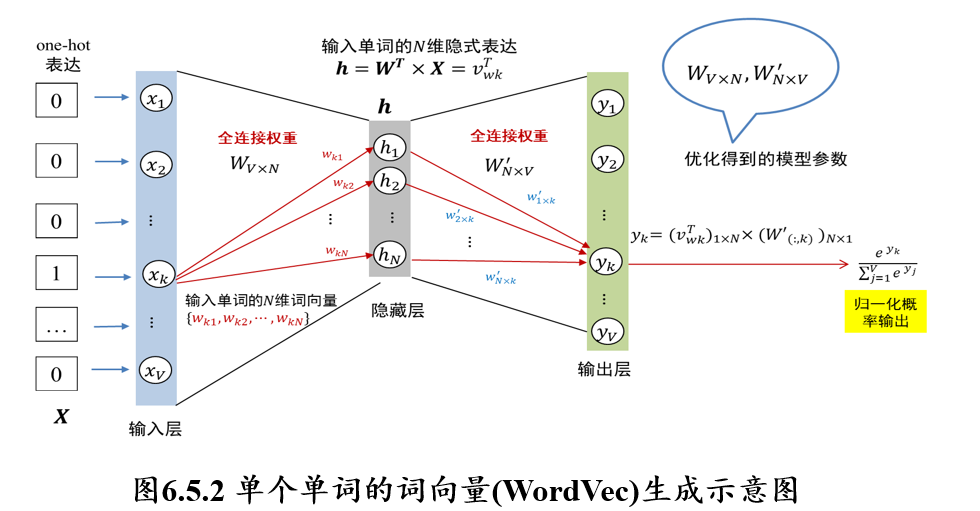
假设词典中有\(V\)个不同的单词,现在考虑如何生成第\(k\)个单词的\(N\)维词向量
- 首先,将该单词表示成\(V\)维one-hot向量\(X\),向量\(X\)中第\(k\)个位置取值为1、其余位置取值均为0,one-hot向量\(X\)表示词典中的一个单词
- 隐藏层神经元大小为\(N\),每个神经元记为\(h_i (1≤i≤N)\)
- 向量\(X\)中每个\(x_i (1≤i≤V)\)与隐藏层神经元是全连接,连接权重矩阵为\(W_{V×N}\)
- 输出层是\(V\)维归一化的概率值,其中\(y_k\)对应第\(k\)个单词归一化的概率值,显然其取值应该远大于其它输出所对应的归一化概率值
因此,某个输入单词对应的\(N\)维词向量为:\([w_{k1},w_{k2},...,w_{kN}]\)

训练词向量模型的目标为:

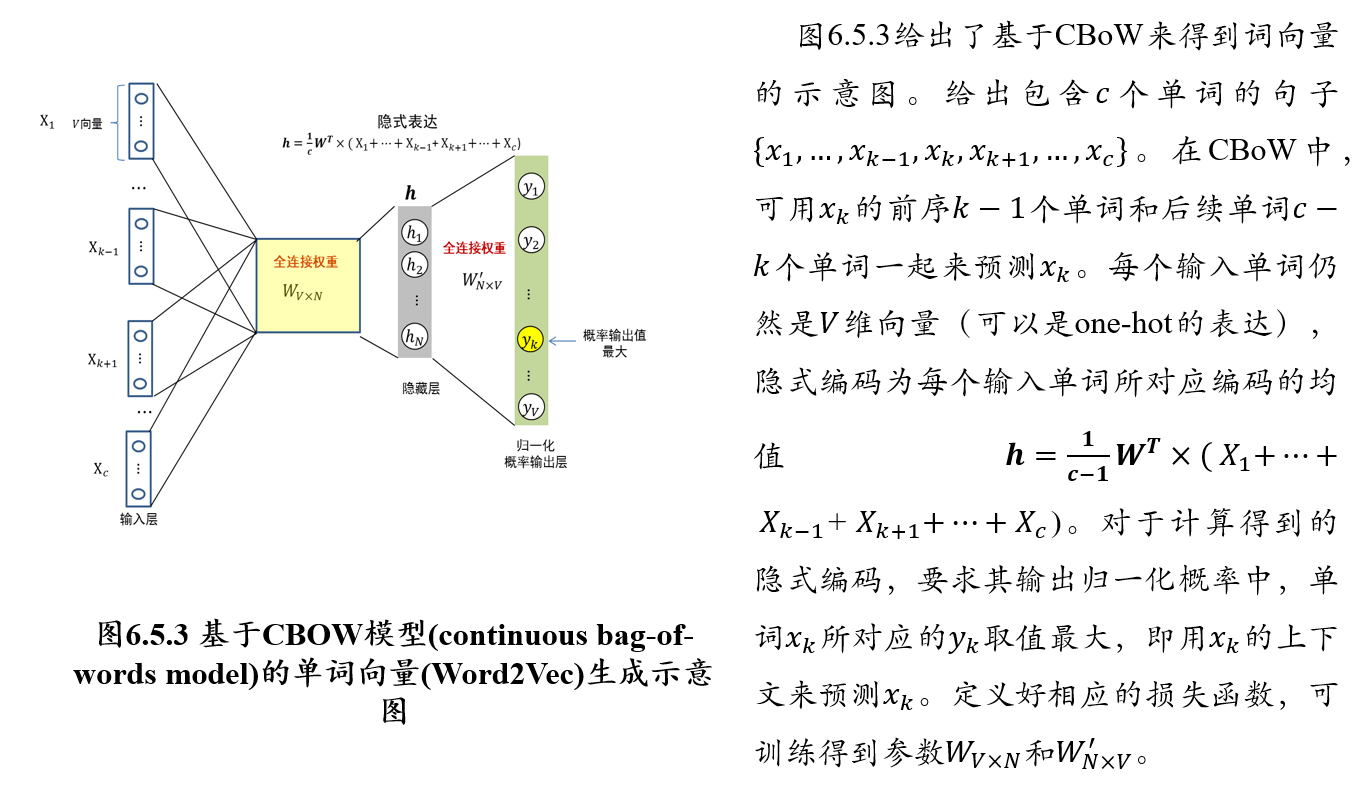
5.6.3 CBOW模型:通过上下文预测单词

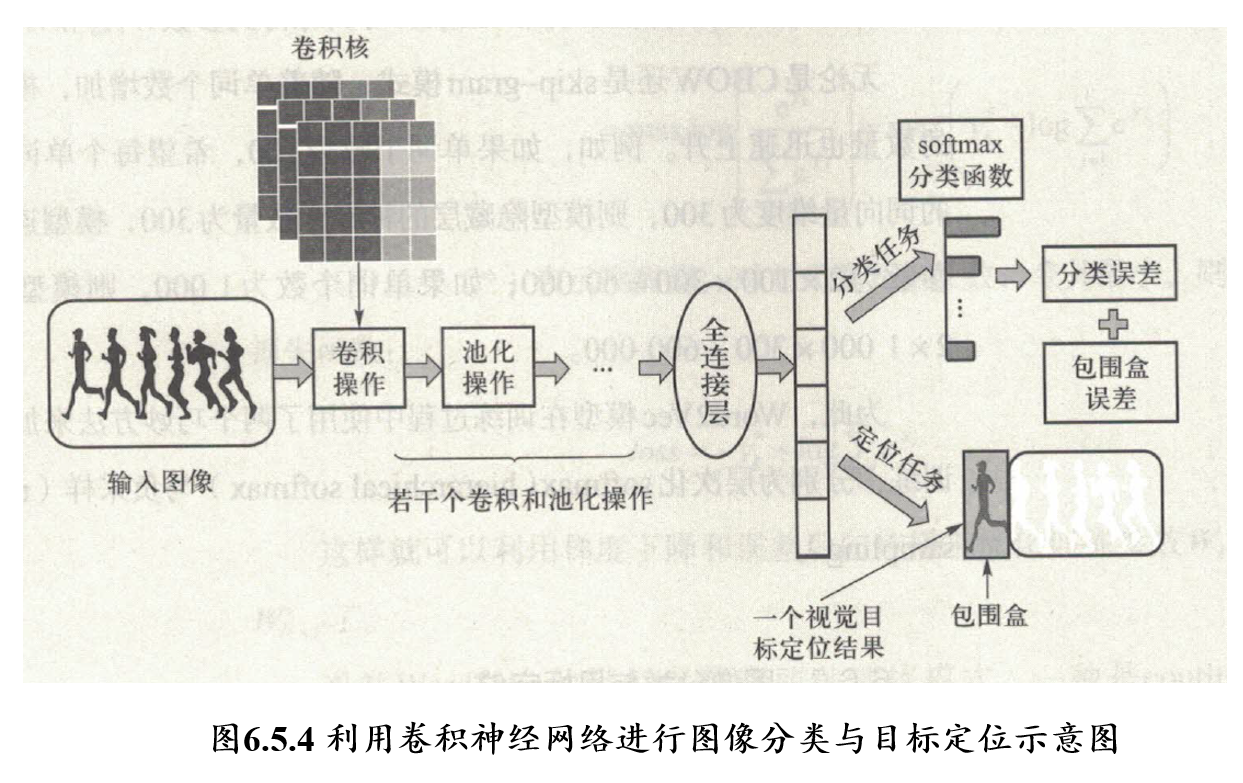
5.6.4 图像分类和目标定位
六、强化学习
6.1 强化学习问题定义
6.1.1 强化学习中的概念
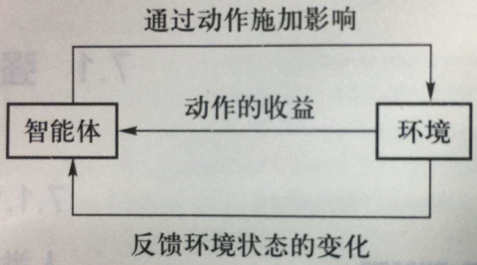
- 智能体(agent):智能体是强化学习算法的主体,它能够根据经验做出主观判断并执行动作,是整个智能系统的核心
- 环境(environment):智能体以外的一切统称为环境,环境在与智能体的交互中,能被智能体所采取的动作影响,同时环境也能向智能体反馈状态和奖励
- 状态(state):状态可以理解为智能体对环境的一种理解和编码,通常包含了对智能体所采取决策产生影响的信息
- 动作(action):动作是智能体对环境产生影响的方式
- 策略(policy):策略是智能体在所处状态下去执行某个动作的依据,即给定一个状态,智能体可根据一个策略来选择应该采取的动作
- 奖励(reward):奖励是智能体序贯式采取一系列动作后从环境获得的收益
6.1.2 强化学习的特点
- 基于评估:强化学习利用环境评估当前策略,以此为依据进行优化
- 交互性:强化学习的数据在与环境的交互中产生
- 序列决策过程:智能主体在与环境的交互中需要作出一系列的决策,这些决策往往是前后关联的
- 注:现实中强化学习问题往往还具有奖励滞后,基于采样的评估等特点
6.1.3 马尔可夫决策过程
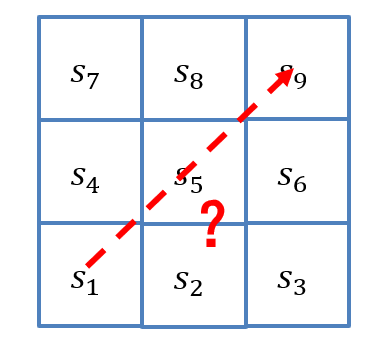
序列优化问题描述:
- 在下图网格中,假设有一个机器人位于\(s_1\),其每一步只能向上或向右移动一格,跃出方格会被惩罚(且游戏停止)
- 如何使用强化学习找到一种策略,使机器人从\(s_1\)到达\(s_9\)?
| 智能主体 Agent | 迷宫机器人 |
|---|---|
| 环境 | 3×3方格 |
| 状态 | 机器人当前时刻所处方格 |
| 动作 | 每次移动一个方格 |
| 奖励 | 到达\(s_9\)时给予奖励,越界时给予惩罚 |
6.1.3.1 离散马尔可夫过程 Discrete Markov Process
离散随机过程:一个随机过程实际上是一系列随时间变化的随机变量,其中当时间是离散量时,一个随机过程可以表示为\(\{X_t\}_{t=0,1,2...}\),其中每个\(X_t\)都是一个随机变量,这被称为离散随机过程
马尔科夫链:满足马尔可夫性质的离散随机过程。也被称为离散马尔可夫过程
- 马尔可夫性质:t+1时刻状态仅与t时刻状态相关
\[ P(X_{t+1}=x_{t+1}|X_0=x_0,X_1=x_1,...,X_t=x_t)=P(X_{t+1}=x_{t+1}|X_t=x_t) \]
6.1.3.2 马尔可夫奖励过程 Markov Reward Process:引入奖励
6.1.3.2.1 奖励机制
为了在序列决策中对目标进行优化,在马尔可夫随机过程框架中加入了奖励机制:
- 奖励函数\(𝑹:𝑺×𝑺↦ℝ\),其中\(𝑹(𝑺_𝒕,𝑺_{𝒕+𝟏})\)描述了从第\(𝒕\)步状态转移到第\(𝒕+𝟏\)步状态所获得奖励
- 在一个序列决策过程中,不同状态之间的转移产生了一系列的奖励\((𝑹_𝟏,𝑹_𝟐,⋯)\),其中\(𝑹_{𝒕+𝟏}\)为\(𝑹(𝑺_𝒕,𝑺_{𝒕+𝟏})\)的简便记法。
- 引入奖励机制,这样可以衡量任意序列的优劣,即对序列决策进行评价。
6.1.3.2.2 反馈、折扣系数
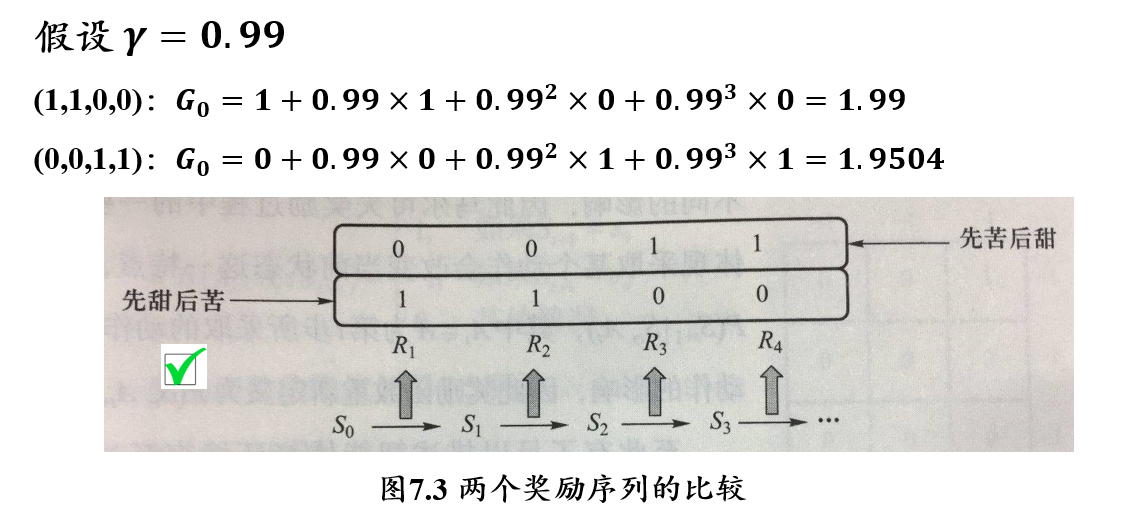
问题:给定两个因为状态转移而产生的奖励序列\((𝟏,𝟏,𝟎,𝟎)\)和\((𝟎,𝟎,𝟏,𝟏)\),哪个奖励序列更好?
- 反馈 Return:反应累加奖励,\(G_t=R_{t+1}+\gamma R_{t+w}+\gamma^2 R_{t+3}+...\)
- 折扣系数 discount factor:\(\gamma \in [0,1]\)
- 反馈值反映了某个时刻后所得到累加奖励,当衰退系数小于1时,越是遥远的未来对累加反馈的贡献越少
6.1.3.3 马尔可夫决策过程 Markov Decision Process:引入动作
在强化学习问题中,智能主体与环境交互过程中可自主决定所采取的动作,不同动作会对环境产生不同影响,为此:
- 定义智能主体能够采取的动作集合为\(𝑨\)
- 由于不同的动作对环境造成的影响不同,因此状态转移概率定义为\(𝑷(𝑺_{𝒕+𝟏}│𝑺_𝒕,𝒂_𝒕 )\),其中\(𝒂_𝒕∈𝑨\)为第\(𝒕\)步采取的动作
- 奖励可能受动作的影响,因此修改奖励函数为\(𝑹(𝑺_𝒕,𝒂_𝒕,𝑺_{𝒕+𝟏})\)
- 动作集合\(𝑨\)可以是有限的,也可以是无限的
- 状态转移可是确定(deterministic)的,也可以是随机概率性(stochastic)的。
- 确定状态转移相当于发生从\(𝑺_𝒕\)到\(𝑺_{𝒕+𝟏}\)的转移概率为1

6.1.3.4 使用离散马尔可夫过程描述机器人移动问题
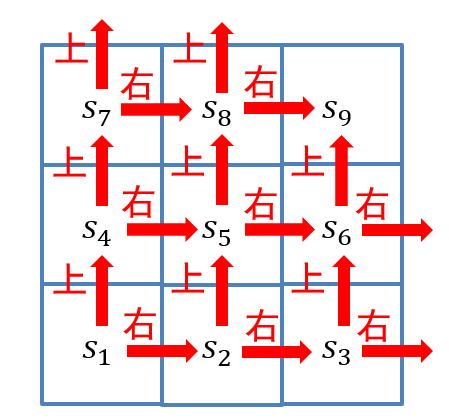
- 随机变量序列\(\{S_t\}_{t=0,1,2,...}\):\(S_t\)表示机器人第\(t\)步的位置(即状态),每个随机变量\(S_t\)的取值范围为\(S={s_1,s_2,⋯, s_9,s_d}\)
- 动作集合:\(A=\{上,右\}\)
- 状态转移概率\(P(S_{t+1} |S_t,a_t)\):满足马尔可夫性,其中\(a_t\in A\),状态转移如图所示
- 奖励函数:\(R(S_t,a_t,S_{t+𝟏} )\),从\(S_t\)采取行动\(a_t\)到\(S_{t+1}\)所获得奖励
- 衰退系数:\(\gamma∈[0, 1]\)
- 综上,可以使用\(MDP=\{S, A, P, R, \gamma\}\)来刻画马尔可夫决策过程

马尔可夫过程中产生的状态序列称为轨迹(trajectory),可以如下表示: \[ (S_0,a_0,R_1,S_1,a_1,R_2,...,S_T) \]
- 轨迹长度可以是无限的,也可以有终止状态\(S_T\)
- 有终止状态的问题叫做分段的(episodic, 即存在回合的),否则叫做持续的(continuing)
- 分段问题中,一个从初始状态到终止状态的完整轨迹称为一个片段或回合(episode)。如围棋对弈中一个胜败对局为一个回合
6.1.4 强化学习中的策略学习
策略函数:
- 策略函数\(𝜋:𝑆×𝐴↦[0, 1]\),其中\(𝜋(𝑠,𝑎)\)的值表示在状态\(s\)下采取动作\(a\)的概率。
- 策略函数的输出可以是确定的,即给定\(s\)情况下,只有一个动作\(a\)使得概率\(𝜋(𝑠,𝑎)\)取值为1
- 对于确定的策略,记为\(𝑎=𝜋(𝑠)\)
6.1.5 强化学习问题定义
- 给定一个马尔可夫决策过程\(MDP=(S,A,P,R,\gamma)\),学习一个最优策略\(\pi^*\),对于任意\(s\in S\),使得\(V_{\pi^*}(s)\)的值最大
- 策略函数:\(𝜋:𝑆×𝐴↦[0, 1]\),\(𝜋(𝑠,𝑎)\)表示智能体在状态\(𝑠\)下采取动作\(𝑎\)的概率
- 最大化每一时刻的回报值:\(G_t=R_{t+1}+\gamma R_{t+w}+\gamma^2 R_{t+3}+...\)
- 价值函数:\(𝑉:𝑆↦R\),其中\(𝑉_𝜋 (𝑠)=𝔼_𝜋 [𝐺_𝑡 |𝑆_𝑡=𝑠]\)
- 表示在第\(t\)步状态为\(s\)时,按照策略\(\pi\)行动后,在未来所获得反馈值的期望
- 动作-价值函数:\(𝑞:𝑆×𝐴↦R\),其中\(𝑞_𝜋 (𝑠,𝑎)= E_𝜋 [𝐺_𝑡 |𝑆_𝑡=𝑠,𝐴_𝑡=𝑎]\)
- 表示在第𝑡步状态为𝑠时,按照策略𝜋采取动作𝑎后,在未来所获得反馈值的期望
- 价值函数和动作-价值函数反映了智能体在某一策略下所对应状态序列获得回报的期望,它比回报本身更加准确地刻画了智能体的目标
- 价值函数和动作-价值函数的定义之所以能够成立,离不开决策过程所具有的马尔可夫性,即当位于当前状态\(s\)时,无论当前时刻\(t\)的取值是多少,一个策略回报值的期望是一定的。当前状态只与前一状态有关,与时间无关
6.1.6 贝尔曼方程 <=> 动态规划方程
Bellman Equation <=> Dynamic Programming Equation
价值函数:\(V_\pi(s)=E_\pi [R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+... |S_t=s]\)
动作-价值函数:\(q_\pi(s,a)=E_\pi [R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+... |S_t=s, A_t=a]\)

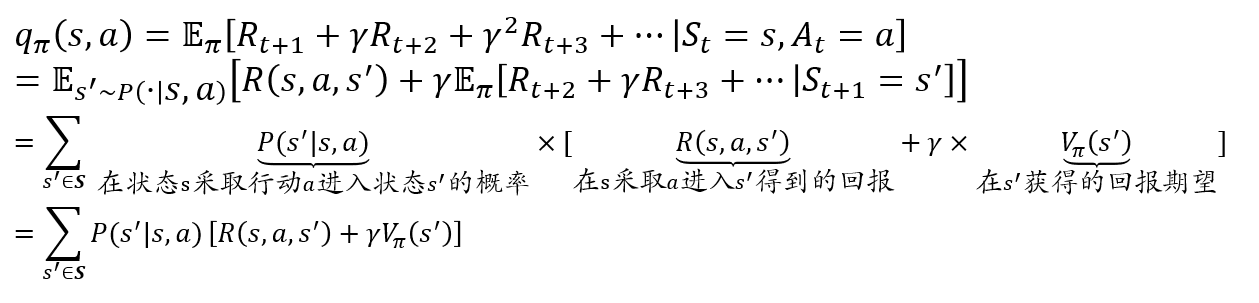
贝尔曼方程:
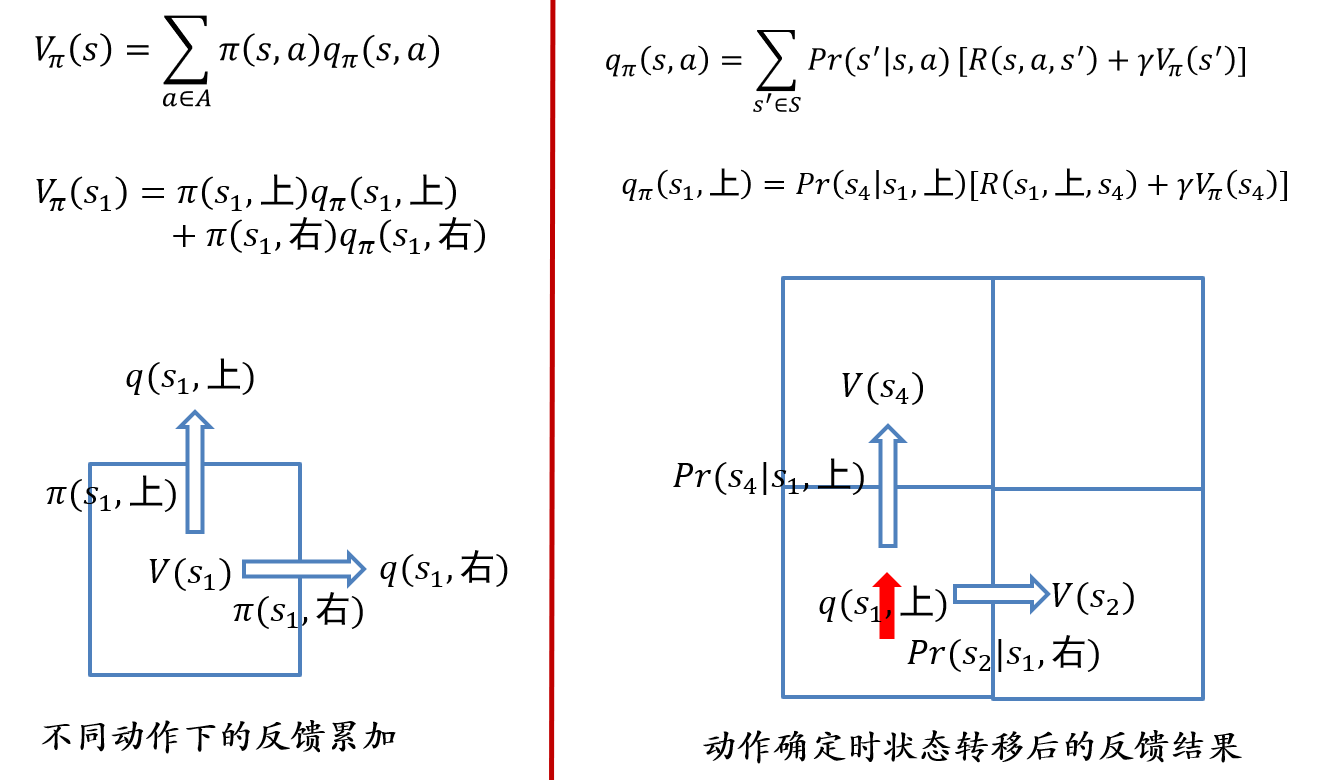
价值函数的贝尔曼方程: \[ V_\pi(s)=\sum_{a\in A}\pi(s,a)q_\pi(s,a) \]
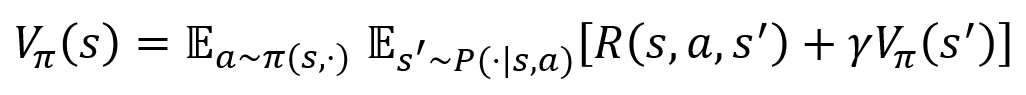
- 描述了当前状态价值函数和其后续状态价值函数之间的关系
- 即当前状态价值函数等于瞬时奖励的期望加上后续状态的(折扣)价值函数的期望
动作-价值函数的贝尔曼方程: \[ q_\pi(s,a)=\sum_{s'\in S}P(s'|s,a)[R(s,a,s')+\gamma V_\pi(s')] \]
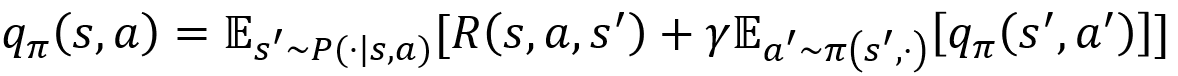
- 描述了当前动作-价值函数和其后续动作-价值函数之间的关系
- 即当前状态下的动作-价值函数等于瞬时奖励的期望加上后续状态的(折扣)动作-价值函数的期望
6.2 基于价值的强化学习
强化学习问题的定义:
- 给定一个马尔可夫决策过程\(MDP=(S,A,P,R,\gamma)\)
- 学习一个最优策略\(\pi^*\),对于任意\(s\in S\),使得\(V_{\pi^*}(s)\)的值最大
6.2.1 策略迭代
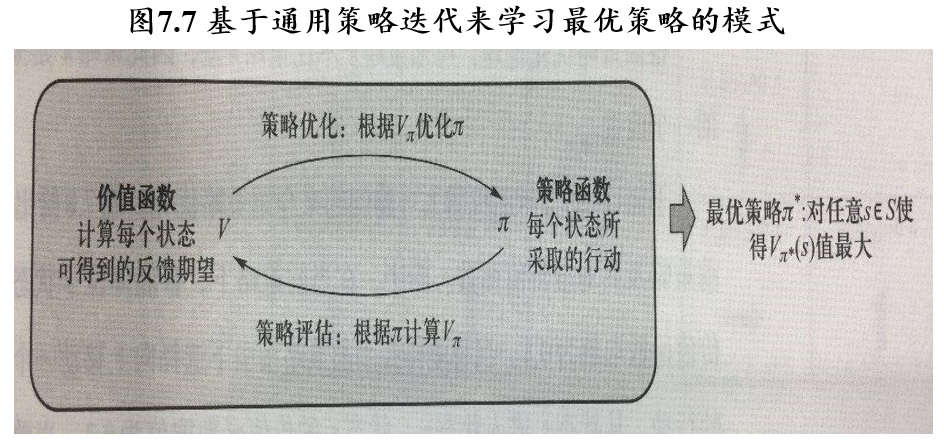
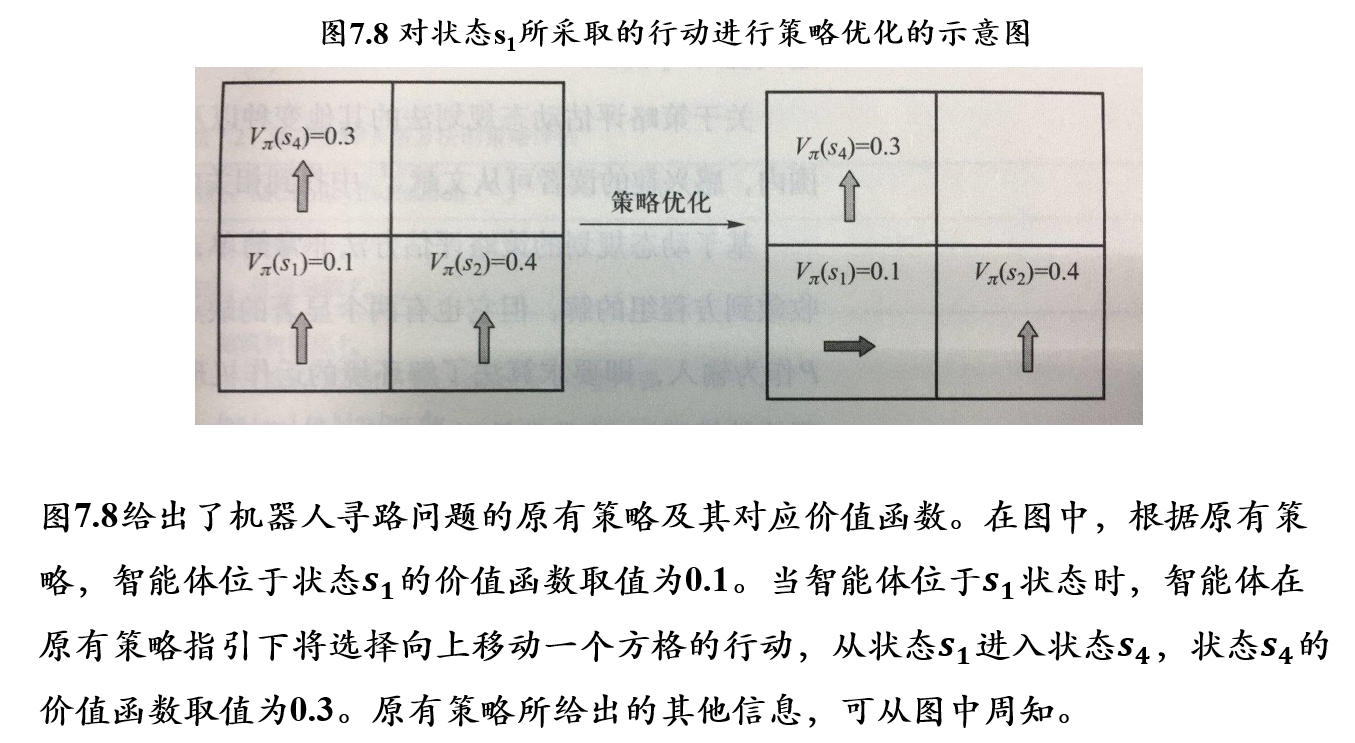
- 从一个任意的策略开始,首先计算该策略下价值函数(或动作-价值函数),然后根据价值函数调整改进策略使其更优,不断迭代这个过程直到策略收敛
- 通过策略计算价值函数的过程叫做策略评估(policy evaluation)
- 通过价值函数优化策略的过程叫做策略优化(policy improvement)
- 策略评估和策略优化交替进行的强化学习求解方法叫做通用策略迭代(Generalized Policy Iteration,GPI)
6.2.2 强化学习中的策略优化
策略优化定理:
- 对于确定的策略\(\pi\)和\(\pi'\),如果对于任意状态\(s\in S\),均有\(q_\pi(s,\pi'(s)) \ge q_\pi(s,\pi(s))\)
- 那么对于任意状态\(s\in S\),有\(V_{\pi'}(s) \ge V_{\pi}(s)\)
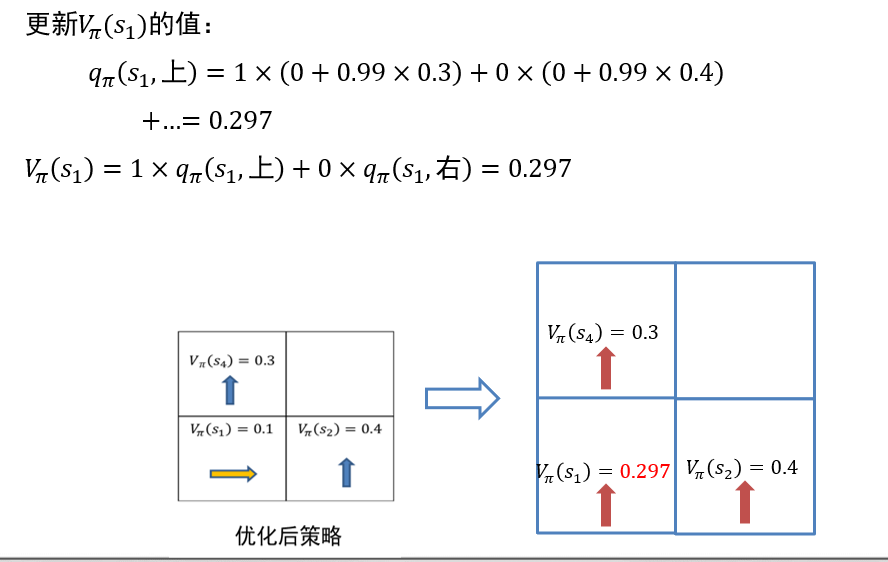
给定当前策略\(\pi\)、价值函数\(V_\pi\)、行动-价值函数\(q_\pi\),构造新策略\(\pi'\)满足如下条件: \[ \forall s \in S,\pi'(s)=argmax_a\ q_{\pi}(s,a) \]
- 则\(\pi'\)就是对\(\pi\)的一个改进
- 于是对于\(\forall s \in S\),有:
\[ q_\pi(s,\pi'(s))=q_\pi(s,argmax_a\ q_\pi(s,a))=max_{a}\ q_\pi(s,a) \ge q_\pi(s,\pi(s)) \]
6.2.3 强化学习中的策略评估方法
假定当前策略为\(𝜋\),策略评估指的是:根据策略\(𝜋\)来计算相应的价值函数\(𝑉_𝜋\)或动作-价值函数\(𝑞_𝜋\)。
这里将介绍在状态集合有限前提下三种常见的策略评估方法,它们分别是
- 动态规划
- 蒙特卡洛采样
- 时序差分(temporal difference)
6.2.3.1 动态规划
基于动态规划的价值函数更新:使用迭代的方法求解贝尔曼方程组

缺点:
- agent需要事先知道状态转移概率\(Pr(s'|s,a)\)
- 无法处理状态集合大小无限的情况
6.2.3.2 蒙特卡洛采样
基于蒙特卡洛采样的价值函数更新:
- 轨迹:从当前状态出发,不停采样,直到到达终止状态

优点:
- agent不必知道状态转移的概率
- 容易扩展到无限状态集合的问题中
缺点:
- 状态集合比较大时,一个状态在轨迹可能非常稀疏,不利于估计期望
- 在实际问题中,最终反馈需要在终止状态才能知晓,导致反馈周期较长
6.2.3.3 时序差分 Temporal Difference
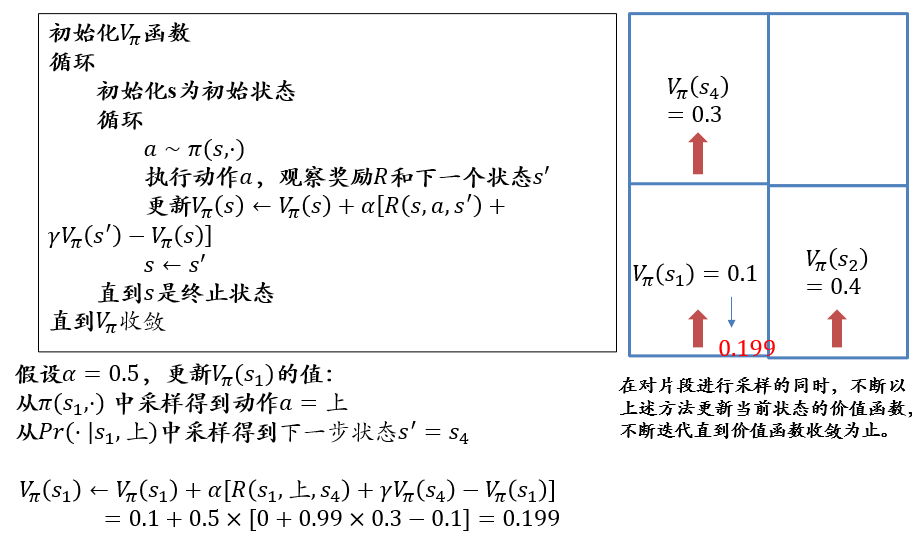
\[ \begin{aligned} V_\pi(s) &← (1-\alpha)V_\pi(s) + \alpha[R+\gamma V_\pi(s')]\\ &= V_\pi(s) + \alpha[R+\gamma V_\pi(s')-V_\pi(s)] \end{aligned} \]
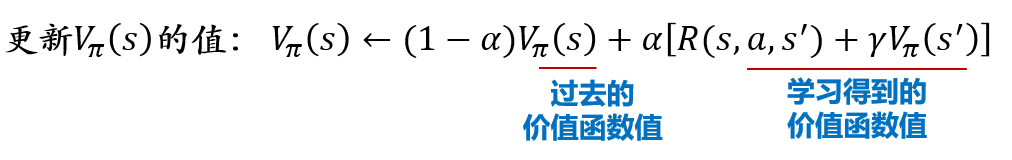

- 时序差分法可以看作蒙特卡罗方法和动态规划方法的有机结合
- 时序差分算法与蒙特卡洛方法相似之处在于:时序差分方法从实际经验中获取信息,无需提前获知环境模型的全部信息
- 时序差分算法与动态规划方法的相似之处在于:时序差分方法能够利用前序已知信息来进行在线实时学习,无需等到整个片段结束(终止状态抵达)再进行价值函数的更新
- 动态规划法根据贝尔曼方程迭代更新价值函数,要求算法事先知道状态之间的转移概率,这往往是不现实的。为了解决这个问题,时序差分法借鉴蒙特卡洛法思想,通过采样动作\(a\)和下一状态\(s'\)来估计计算\(V_\pi(s)\)
- 由于通过采样进行计算,所得结果可能不准确,因此时序差分法并没有将这个估计值照单全收,而是以\(\alpha\)作为权重来接受新的估计值,即把价值函数更新为\((1−𝛼)𝑉_𝜋(𝑠)+𝛼[𝑅+𝛾𝑉_𝜋 (s')]\)
- 对这个式子稍加整理就能得到算法中的形式:\(𝑉_𝜋(𝑠)←𝑉_𝜋(𝑠)+𝛼[𝑅+𝛾𝑉_𝜋(s')−𝑉_𝜋(𝑠)]\)
- 时序差分目标:\(𝑅+𝛾𝑉_𝜋(𝑠')\)
- 时序差分偏差:\(𝑅+𝛾𝑉_𝜋(𝑠')−𝑉_𝜋(𝑠)\)
- 时序差分法和蒙特卡洛法都是通过采样若干个片段来进行价值函数更新的,但是时序差分法并非使用一个片段中的终止状态所提供的实际回报值来估计价值函数,而是根据下一个状态的价值函数来估计价值函数,这样就克服了采样轨迹的稀疏性可能带来样本方差较大的不足问题,同时也缩短了反馈周期
6.2.3.4 Q-learning:直接计算\(q_\pi\)
\[ \begin{aligned} q_\pi(s,a) &← (1-\alpha)q_\pi(s,a) + \alpha[R+\gamma \max_{a'} q_\pi(s',a')]\\ &= q_\pi(s,a) + \alpha[R+\gamma \max_{a'} q_\pi(s',a')-q_\pi(s,a)] \end{aligned} \]

- Q-learning中直接记录和更新动作-价值函数\(q_\pi\)
- 这是因为策略优化要求已知动作-价值函数\(q_\pi\),如果算法仍然记录值函数\(V_\pi\),在不知道状态转移概率的情况下将无法求出\(q_\pi\)
- 于是,Q-learning中,只有动作-价值函数(即q函数)参与计算
6.2.3.5 ε-greedy策略:策略学习中探索与利用的平衡


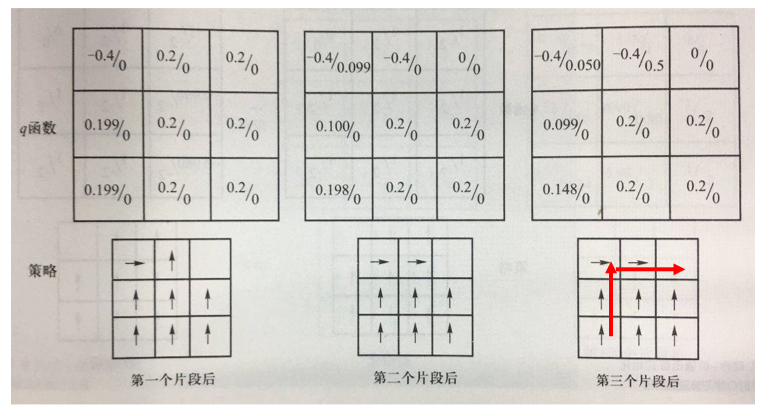
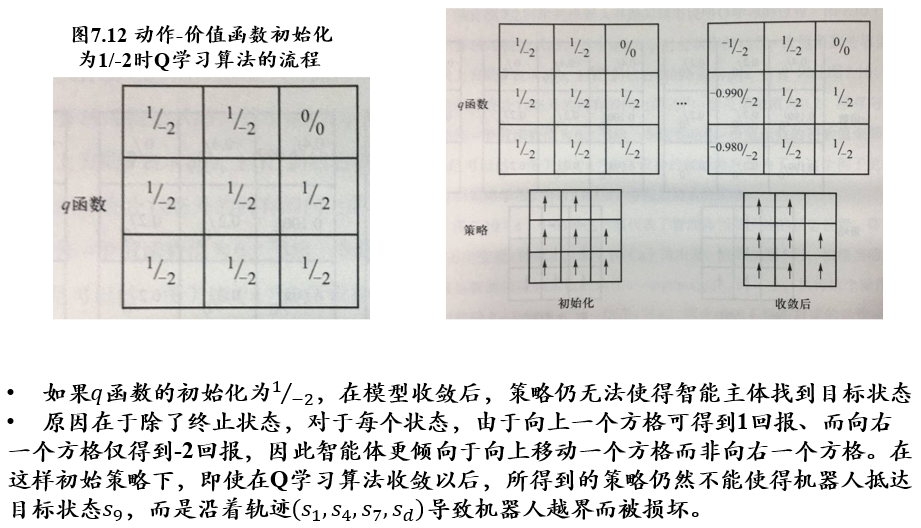
- ε-greedy策略:大体上遵循最优策略的决定,偶尔(以ε的概率)进行探索
- 如上一个例子中,如果偶尔在某些状态随机选择"向右移动一个方格"的动作,则可克服机器人无法走到终点\(s_9\)这一不足
- 将动作采样从"确定地选取最优动作" 改为 ”按照ε-greedy策略选取动作“
- 更新时仍保持用max操作选取最佳策略
- 像这样,更新时的目标策略与采样策略不同的方法,称为离策略 off-policy方法
6.2.3.6 Deep Q-learning:用神经网络拟合\(q_\pi\)
思路:将q函数参数化,用一个非线性回归模型来拟合q函数
- 能够用有限的参数刻画无限的状态
- 由于回归函数的连续性,没有探索过的状态也可以通过周围状态来估计

- 损失函数刻画了q的估计值\(R+\gamma\ max_{a'}q_\pi(s',a';\theta)\)与当前值的平方误差
- 利用梯度下降算法优化参数\(\theta\)
- 如果使用深度神经网络来拟合q函数,则该算法称为Deep Q-learning/深度强化学习
(不考)6.3 基于策略的强化学习
基于价值的强化学习:
- 以对价值函数/动作-价值函数的建模为核心
基于策略的强化学习:
- 直接参数化策略函数,求解参数化的策略函数的梯度
- 策略函数的参数化可以表示为\(𝝅_𝜽 (𝒔,𝒂)\),其中\(𝜽\)为一组参数,函数取值表示在状态\(𝒔\)下选择动作\(𝒂\)的概率
- 和Q学习的\(𝝐\)贪心策略相比,这种参数化的一个显著好处是:选择一个动作的概率是随着参数的改变而光滑变化的,实际上这种光滑性对算法收敛有更好的保证。
(不考)6.3.1 策略梯度定理
最大化目标: \[
MAX\ J(\theta)=V_{\pi_\theta}(s_0), 从初始状态出发的价值函数
\] 策略梯度定理: \[
∇_\theta J(\theta) \propto \sum_s\mu_{\pi_\theta}(s)\sum_a
q_{\pi_\theta}(s,a)∇_\theta\pi_\theta(s,a)
\]

(不考)6.3.2 基于蒙特卡洛采样的策略梯度法




(不考)6.3.3 基于时序差分的策略梯度法:Actor-Critic


(不考)6.4 深度强化学习的应用
(不考)6.4.1 Deep Q-Learning:围棋博弈
围棋游戏的一个片段的轨迹
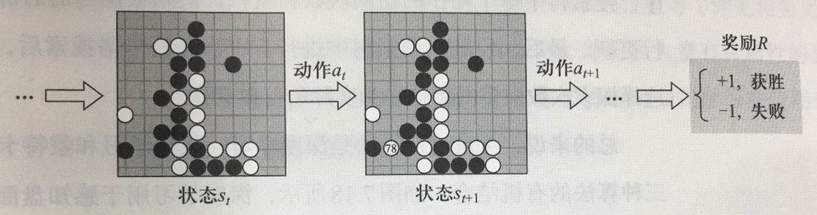
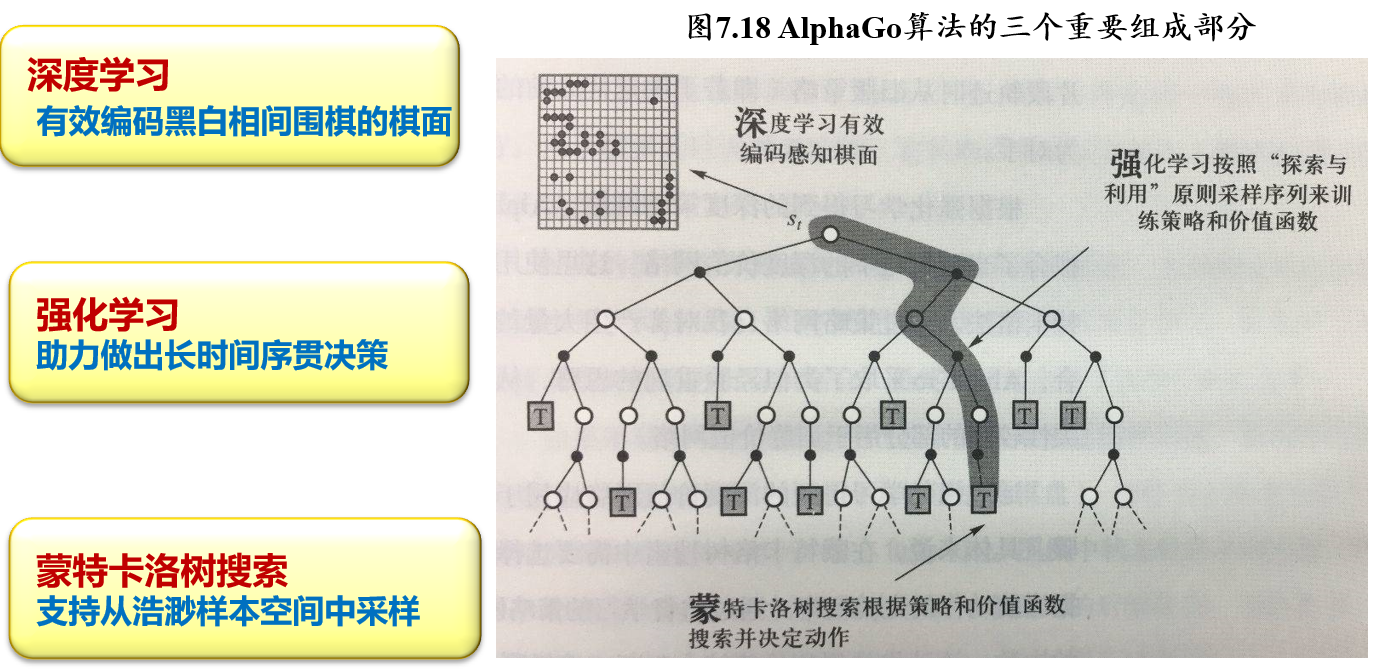
(不考)6.4.2 Deep Q-Learning:雅达利游戏
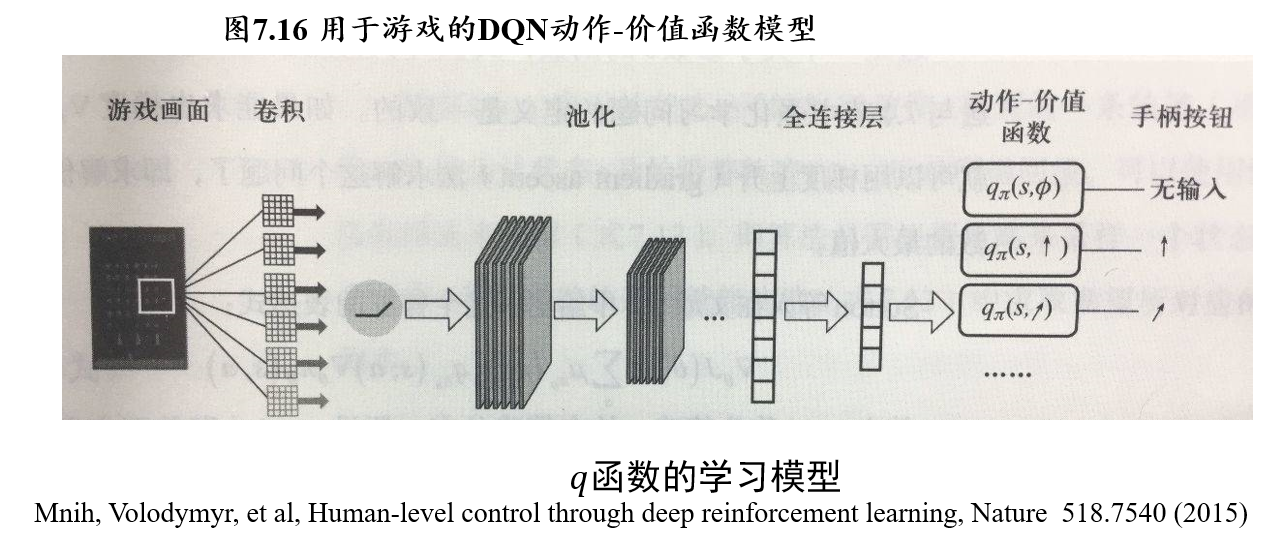
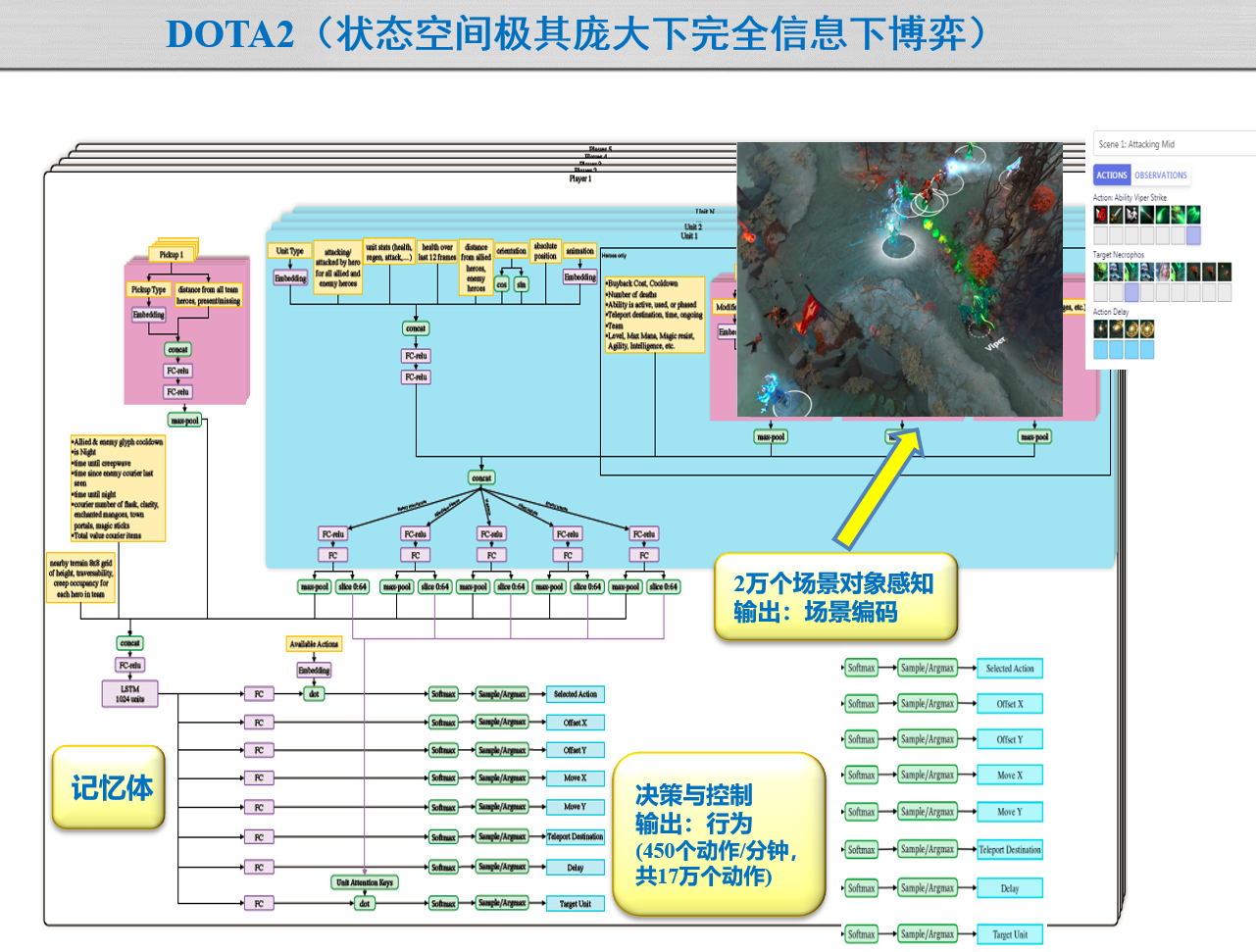
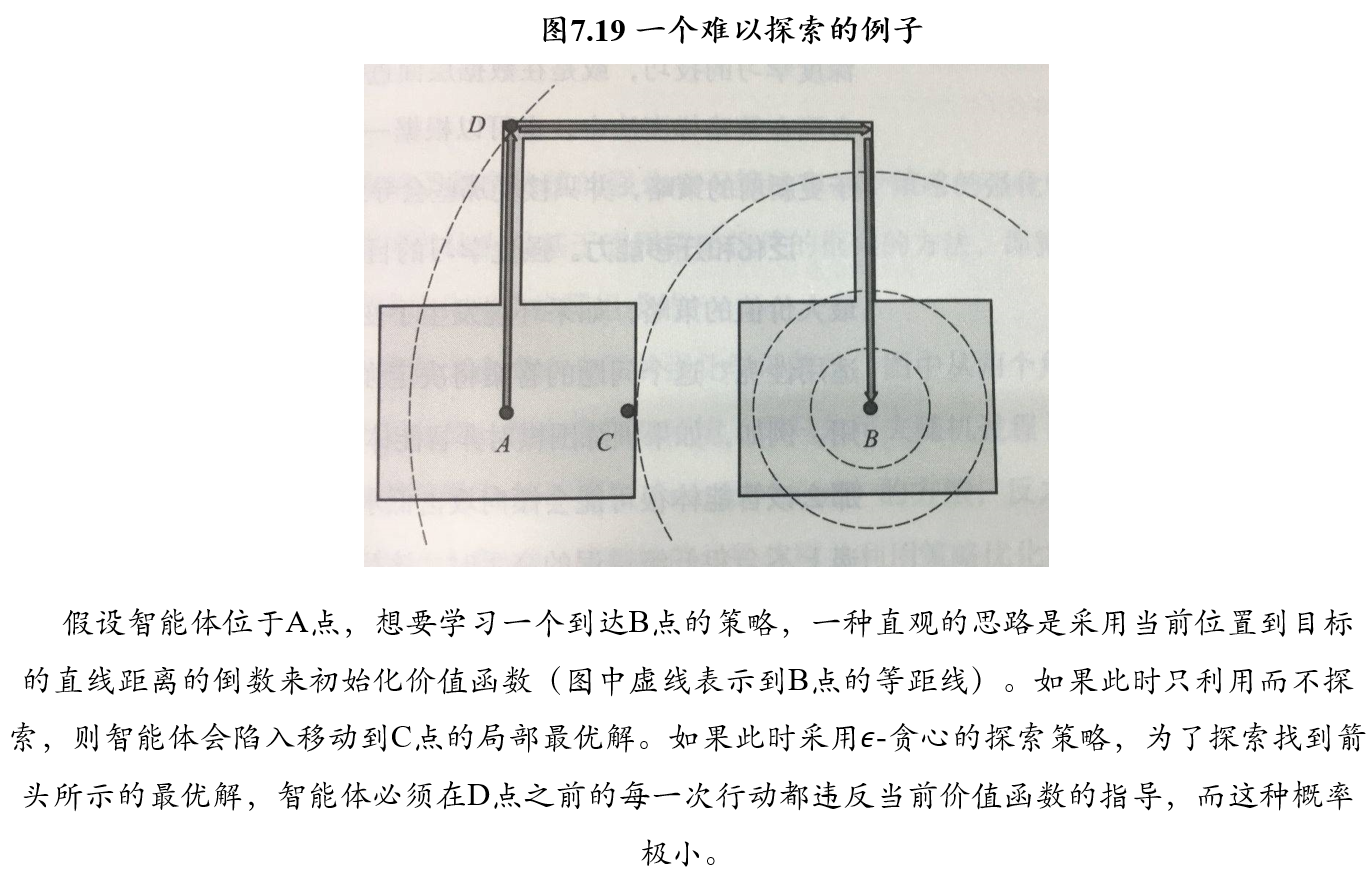
(不考)6.4.3 难以探索的例子
6.5 强化学习的分类
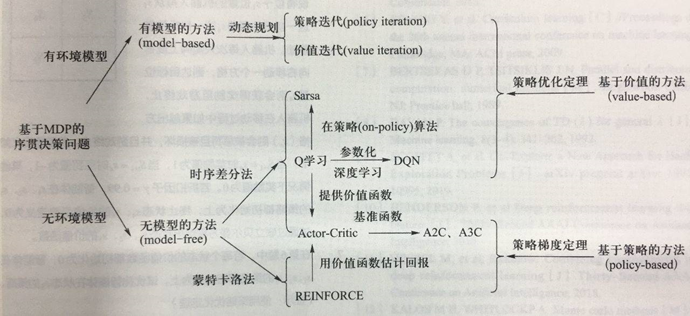
图中从两个角度对强化学习算法做了分类 1. 其中依靠对环境(即马尔可夫随机过程)的先验知识或建模的算法称为基于模型(Model-based)的方法,反之称为无模型的方法(Model-free) 2. 只对价值函数建模并利用策略优化定理求解的方法称为基于价值(Value-based)的方法,对策略函数建模并利用策略梯度定理求解的方法称为基于策略(Policy-based)的方法
七、人工智能博弈
7.1 博弈论的相关概念
7.1.1 博弈的要素
- 参与者/玩家 player:参与博弈的决策主体
- 策略
strategy:参与者可以采取的行动方案,是在采取行动之前就已经准备好的完整方案
- 每个参与者可采纳策略的全体组合形成了策略集 strategy set
- 所有参与者各自采取行动后形成的状态被称为局势 outcome
- 如果参与者可以通过一定概率分布来选择若干个不同的策略,这样的策略称为混合策略 mixed strategy。
- 若参与者每次行动都选择某个确定的策略,这样的策略称为纯策略 pure strategy
- 收益 payoff:各个参与者在不同局势下得到的利益
- 混合策略意义下的收益应为期望收益 expected payoff
- 规则 rule:对参与者行动的先后顺序、参与者获得信息多少等内容的规定
7.1.2 研究范式
研究范式:建模者对参与者规定可采取的策略集和取得的收益,观察当参与者选择若干策略以最大化其收益时会产生什么结果
7.1.3 囚徒困境 Prisoner's Dilemma

- 均衡解:在当前情况下,任意一个人改变策略,而其他人保持不变,改变策略的人得到的收益一定变低
7.1.4 博弈的分类
合作博弈与非合作博弈
- 合作博弈 cooperative game:部分参与者可以组成联盟以获得更大的收益
- 非合作博弈 non-cooperative game:参与者在决策中都彼此独立,不事先达成合作意向
静态博弈与动态博弈
- 静态博弈 static game:所有参与者同时决策,或参与者互相不知道对方的决策
- 动态博弈 dynamic game:参与者所采取行为的先后顺序由规则决定,且后行动者知道先行动者所采取的行为
完全信息博弈与不完全信息博弈
- 完全信息 complete information:所有参与者均了解其他参与者的策略集、收益等信息
- 不完全信息 incomplete information:并非所有参与者均掌握了所有信息
囚徒困境是一种非合作、不完全信息的静态博弈
7.1.5 纳什均衡
博弈的稳定局势即为纳什均衡 Nash equilibrium:
- 指的是参与者所作出的这样一种策略组合,在该策略组合上,任何参与者单独改变策略都不会得到好处
- 换句话说,如果在一个策略组合上,当所有其他人都不改变策略时,没有人会改变自己的策略,则该策略组合就是一个纳什均衡
- 纳什均衡的本质:不后悔
Nash定理:
- 若参与者有限,每位参与者的策略集有限,收益函数为实值函数,则博弈必存在混合策略意义下的纳什均衡
囚徒困境中两人同时认罪就是这一问题的纳什均衡
混合策略纳什均衡:
- 博弈过程中,博弈方通过概率形式随机从可选策略中选择一个策略而达到的纳什均衡
设雇主检查的概率为\(\alpha\),雇员偷懒的概率为\(\beta\),则雇主-雇员之间博弈的期望收益为:
纳什均衡:其他参与者策略不变的情况下,某个参与者单独采取其他策略都不会使得收益增加⇔无论雇主是否检查,雇主的收益都一样;无论雇员是否偷懒,雇员的收益都一样
- 于是有\(𝑻_𝟏=𝑻_𝟐\) 以及\(𝑻_𝟑=𝑻_𝟒\)
- 在纳什均衡下,由于\(𝑻_𝟑=𝑻_𝟒\),可知雇主采取检查策略的概率(雇主趋向于用这个概率去检查):\(𝜶=\frac{𝑯}{𝑾+𝑭}\)
- 在纳什均衡下,由于\(𝑻_𝟏=𝑻_𝟐\),可知雇员采取偷懒策略的概率(雇员趋向于用这个概率去偷懒):\(𝜷=\frac{𝑪}{𝑾+𝑭}\)
- 在检查概率为𝜶之下,雇主的收益:\(𝑻_𝟏=𝑻_𝟐=𝑽−𝑾−\frac{𝑪𝑽}{𝑾+𝑭}\)
- 对上式中\(𝑾\)求导,则当\(𝑾=\sqrt{𝑪𝑽}−𝑭\)时,雇主的收益最大,其值为\(𝑻_{𝒎𝒂𝒙}=𝑽−𝟐\sqrt{𝑪𝑽}+𝑭\)
7.1.6 策梅洛定理
策梅洛定理 Zermelo's theorem:
- 对于任意一个有限步的双人完全信息零和动态博弈,一定存在先手必胜策略或后手必胜策略或双方保平策略
- 策梅洛定理仅对两人博弈有效,如果博弈竞技者超过了2人,如对于三人博弈,策梅洛定理无法保证三方中一定有一方获胜、其他两方必败或者三方和局的策略
(不考)7.2 博弈策略求解
动机
- 博弈论提供了许多问题的数学模型
- 纳什定理确定了博弈过程问题存在解
- 人工智能的方法可用来求解均衡局面或者最优策略
主要问题
- 如何高效求解博弈参与者的策略以及博弈的均衡局势?
应用领域
- 大规模搜索空间的问题求解:围棋
- 非完全信息博弈问题求解:德州扑克
- 网络对战游戏智能:Dota、星球大战
- 动态博弈的均衡解:厂家竞争、信息安全
(不考)7.2.1 虚拟遗憾最小化算法 Regret Minimization
对于一个有\(N\)个玩家参加的博弈,玩家\(i\)在博弈中采取的策略为\(\sigma_i\)
对于所有玩家来说,他们的所有策略构成了一个策略组合,记为\(\sigma=\{\sigma_1,\sigma_2,...,\sigma_N\}\)
策略组中,除玩家\(i\)外,其它玩家的策略组合记为\(\sigma_{-i}=\{\sigma_1,\sigma_2,...,\sigma_{i-1},\sigma_{i+1},...,\sigma_N\}\)
给定策略组合\(\sigma\),玩家\(i\)在终结局势下的收益记为\(u_i(\sigma)\)
在给定其它玩家的策略组合\(\sigma_{-i}\)的情况下,对玩家\(i\)而言的最优反应策略\(\sigma_i^*\)满足如下条件: \[ u_i(\sigma_i^*,\sigma_{-i}) \ge \max_{\sigma_i'\in \sum_i}u_i(\sigma_i',\sigma_{-i}) \]
- \(\sum_i\)是玩家\(i\)可以选择的所有策略
- 如上条件表示当玩家\(i\)采用最优反应策略时,玩家\(i\)能够获得最大收益
(不考)7.2.1.1 纳什均衡策略的定义
在策略组合\(𝜎^∗\)中,如果每个玩家的策略相对于其他玩家的策略而言都是最佳反应策略,那么策略组合\(𝜎^∗\)就是一个纳什均衡策略
- 在有限对手、有限策略情况下,纳什均衡一定存在
- 策略组\(𝜎^∗=\{𝜎_1^∗,𝜎_2^∗,…,𝜎_𝑁^∗\}\)对任意玩家\(𝑖=1,..,𝑁\),满足如下条件:
\[ 𝑢_𝑖(𝜎^∗) ≥ \max_{𝜎_𝑖^′∈Σ_𝑖} 𝜇_𝑖 (𝜎_1^∗,𝜎_2^∗,…,𝜎_𝑖^′,…,𝜎_𝑁^∗) \]
在博弈策略求解的过程中,希望求解得到每个玩家最优反应策略,若所有玩家都是理性的,则算法求解最优反应策略就是一个纳什均衡
考虑到计算资源有限这一前提,难以通过遍历博弈中所有策略组合来找到一个最优反应策略,因此需要找到一种能快速发现近似纳什均衡的方法
(不考)7.2.1.2 遗憾最小化算法
遗憾最小化算法是一种根据以往博弈过程中所得遗憾程度来选择未来行为的方法
在过去\(𝑇\)轮中,玩家\(𝑖\)采取策略\(𝜎_𝑖\)的累加遗憾值定义如下: \[ Regret_i^T (𝜎_i)=\sum_{𝑡=1}^𝑇 (u_i(𝜎_i,𝜎_{−i}^t) − u_i(𝜎^t)) \]
- \(𝜎^𝑡\)表示:第\(𝑡\)轮中所有玩家的策略组合
- \(𝜎_{−𝑖}^𝑡\)表示:第\(𝑡\)轮中除了玩家\(𝑖\)以外的策略组合
简单地说,累加遗憾值代表:
- 在过去\(𝑇\)轮中,玩家\(𝑖\)在每一轮中选择策略\(𝜎_𝑖\)所得收益与采取其他策略所得收益之差的累加
(不考)7.2.1.3 有效遗憾值
在得到玩家\(i\)的所有可选策略的遗憾值后,可以根据遗憾值的大小来选择后续第\(𝑇+1\)轮博弈的策略,这种选择方式被称为遗憾匹配
当然,通常遗憾值为负数的策略被认为不能提升下一时刻收益,所以如下定义有效遗憾值: \[ 𝑅𝑒𝑔𝑟𝑒𝑡_𝑖^{𝑇,+} 𝜎_𝑖=\max (𝑅𝑒𝑔𝑟𝑒𝑡_𝑖^𝑇(𝜎_𝑖),0) \]
利用有效遗憾值的遗憾匹配,可得到玩家\(𝑖\)在第\(T+1\)轮选择策略\(𝜎_𝑖\)的概率\(𝑃(𝜎_𝑖^{T+1})\)为:
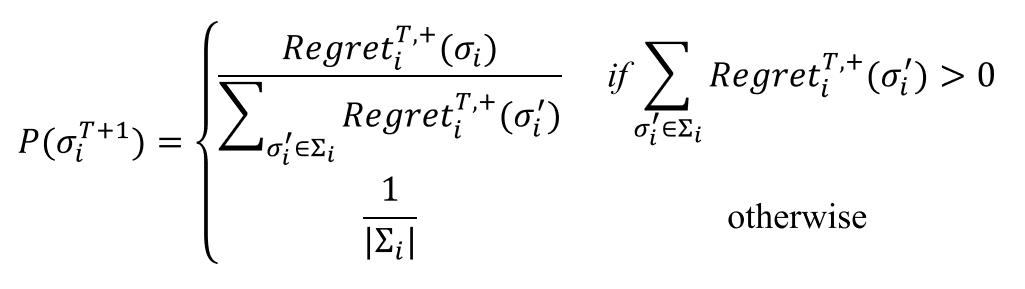
- \(|Σ_i|\)表示玩家\(𝑖\)所有策略的总数
- 显然,如果在过往\(𝑇\)轮中策略\(𝜎_𝑖\)所带来的遗憾值大、其他策略\(𝜎_𝑖^′\)所带来的遗憾值小,则在第\(𝑇+1\)轮选择策略\(𝜎_𝑖\)的概率值\(𝑃(𝜎_𝑖^{𝑇+1})\)就大
- 即:带来越大遗憾值的策略具有更高的价值,因此其在后续被选择的概率就应该越大
- 如果没有一个能够提升前\(T\)轮收益的策略,则在后续轮次中随机选择一种策略
可以依照一定的概率选择行动
- 为了防止对手发现自己所采取的策略,如采取遗憾值最大的策略
(不考)7.2.1.4 计算理论
对于任何序贯决策的博弈对抗,可将博弈过程表示成一棵博弈树,博弈树中的每一个中间节点都是一个信息集\(I\),信息集中包含了博弈中当前的状态
- 给定博弈树的每一个节点,玩家都可以从一系列的动作中选择一个,然后状态发生转换,如此周而复始,直到终局(博弈树的叶子节点)
- 玩家在当前状态下可采取的策略就是当前状态下所有可能动作的一个概率分布
具体而言,在信息集\(𝐼\)下,玩家可以采取的行动集合记作\(𝐴(𝐼)\)
- 玩家\(𝑖\)所采取的行动\(𝑎_𝑖∈𝐴(𝐼)\)可认为是其采取的策略\(𝜎_𝑖\)的一部分
- 在信息集\(𝐼\)下采取行动\(𝑎\)所代表的策略记为\(𝜎_{𝐼→𝑎}\)
- 这样,要计算虚拟遗憾值的对象,就是博弈树中每个中间节点在信息集下所采取的行动,并根据遗憾值匹配得到该节点在信息集下应该采取的策略\(𝜎_{𝐼→𝑎}\)
在一次博弈中,所有玩家交替采取的行动序列记为\(ℎ\)(从根节点到当前节点的路径)
- 对于所有玩家的策略组合\(𝜎\),行动序列ℎ出现的概率记为\(𝜋^𝜎 (ℎ)\),不同的行动序列可以从根节点到达当前节点的信息集\(𝐼\)(即不同决策路径可到达博弈树中同一个中间节点)
- 在策略组合\(𝜎\)下,所有能够到达该信息集的行动序列的概率累加就是该信息集的出现概率,即\(𝜋^𝜎(𝐼)=∑_{ℎ∈𝐼}𝜋^𝜎 (ℎ)\)
博弈的终结局势集合也就是博弈树中叶子节点的集合,记为\(𝑍\)
- 对于任意一个终结局势\(𝑧∈𝑍\),玩家\(𝑖\)在此终点局势下的收益记作\(𝑢_𝑖 (𝑧)\)
- 给定行动序列\(ℎ\),依照策略组合\(𝜎\)最终到达终结局势\(𝑧\)的概率记作\(𝜋^𝜎 (ℎ,𝑧)\)
在策略组合\(𝜎\)下,对玩家\(𝑖\)而言,如下计算从根节点到当前节点的行动序列路径\(ℎ\)的虚拟价值\(v_i(σ,h)\):
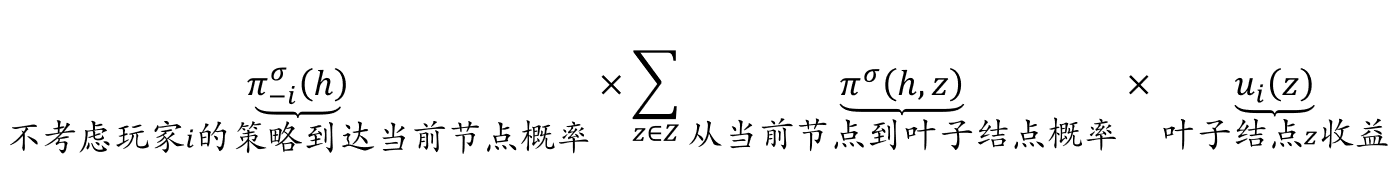
- 在上式中,\(𝜋_{−𝑖}^𝜎(ℎ)\)表示从根节点出发,不考虑玩家\(𝑖\)的策略,仅考虑其他玩家策略而经过路径\(ℎ\)到达当前节点的概率
- 也就是说,即使玩家𝑖有其他策略,总是要求玩家\(𝑖\)在每次选择时都选择路径ℎ中对应的动作,以保证从根节点出发能够到达当前节点
- 可见,行动序列路径ℎ的虚拟价值等于如下三项结果的乘积:不考虑玩家𝑖的策略(仅考虑其他玩家策略)经过路径ℎ到达当前节点的概率、从当前节点走到叶子结点(博弈结束)的概率、所到达叶子节点的收益。
在定义了行动序列路径ℎ的虚拟价值之后,就可如下计算玩家\(𝑖\)在基于路径\(ℎ\)到达当前节点采取行动\(𝑎\)的遗憾值: \[ 𝑟_𝑖 (ℎ,𝑎)=𝑣_𝑖(𝜎_{𝐼→𝑎},ℎ)−𝑣_𝑖 (𝜎,ℎ) \]
- 该遗憾值是玩家\(𝑖\)通过行动序列\(ℎ\)到达当前节点采取行动\(𝑎\)所得虚拟价值减去采用策略\(𝜎\)所得路径\(ℎ\)的虚拟价值
对能够到达同一个信息集\(𝐼\)(即博弈树中同一个中间节点)的所有行动序列的遗憾值进行累加,即可得到信息集\(𝐼\)的遗憾值: \[ 𝑟_𝑖(𝐼,𝑎)=\sum_{ℎ∈𝐼}𝑟_𝑖(ℎ,𝑎) \]
类似于遗憾最小化算法,虚拟遗憾最小化的遗憾值是𝑇轮重复博弈后的累加值: \[ 𝑅𝑒𝑔𝑟𝑒𝑡_𝑖^𝑇 (𝐼,𝑎)=∑_{𝑡=1}^𝑇 𝑟_𝑖^𝑡 (𝐼,𝑎) \]
- \(𝑟_𝑖^𝑡 (𝐼,𝑎)\)表示玩家\(𝑖\)在第\(𝑡\)轮中于当前节点选择行动\(𝑎\)的遗憾值
进一步可以定义有效虚拟遗憾值: \[ 𝑅𝑒𝑔𝑟𝑒𝑡_𝑖^{𝑇,+}(𝐼,𝑎)=\max(𝑅_𝑖^𝑇 (𝐼,𝑎),0) \]
根据有效虚拟遗憾值进行遗憾匹配以计算经过\(𝑇\)轮博弈后,玩家\(𝑖\)在信息集\(𝐼\)情况下于后续\(𝑇+1\)轮选择行动\(𝑎\)的概率:
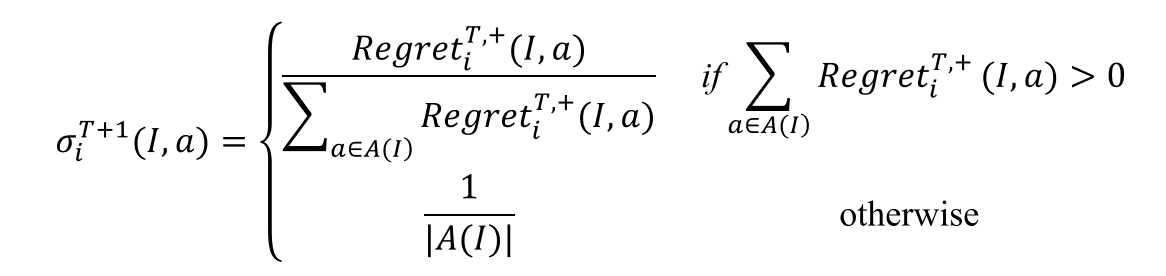
(不考)7.2.1.5 虚拟最小化算法步骤
在虚拟最小化算法的求解过程中,同样需要反复模拟多轮博弈来拟合最佳反应策略,算法步骤如下
- 初始化遗憾值和累加策略表为0
- 采用随机选择的方法来决定策略
- 利用当前策略与对手进行博弈
- 计算每个玩家采取每次行为后的遗憾值
- 根据博弈结果计算每个行动的累加遗憾值大小来更新策略
- 重复3)到5)步若干次,不断的优化策略
- 根据重复博弈最终的策略,完成最终的动作选择
(不考)7.2.1.6 示例
双人库恩扑克游戏
规则:

先手玩家A对应的博弈树
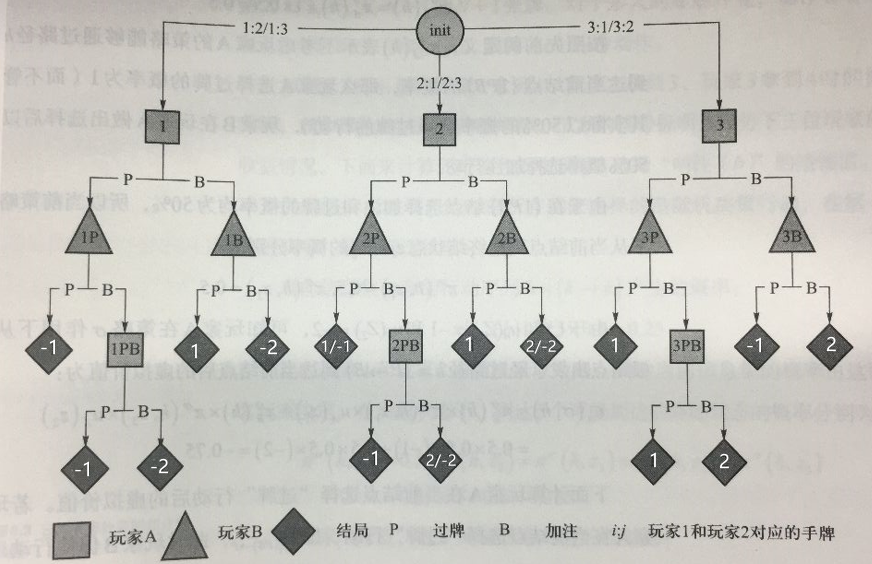


计算节点\(\{1PB\}\)的虚拟价值:

计算玩家A在节点\(\{1PB\}\)选择过牌行动后的虚拟价值:

计算玩家A在节点\(\{1PB\}\)选择过牌行动后的虚拟遗憾值:

7.3 博弈规则设计
7.3.1 研究的问题
- 在现实生活中,如果所有博弈者都追求自己利益最大化,很可能会导致两败俱伤的下场
- 那么应该如何设计博弈的规则使得博弈的最终局势能尽可能达到整体利益的最大化呢?
7.3.2 双边匹配算法
- 在生活中,人们常常会碰到与资源匹配相关的决策问题(如求职就业、报考录取等),这些需要双向选择的情况被称为是双边匹配问题
- 在双边匹配问题中,需要双方互相满足对方的需求才会达成匹配
7.3.2.1 稳定婚姻问题 Stable Marriage Problem

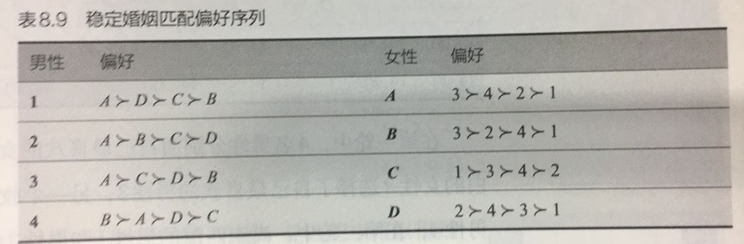
假设有4名单身男性{𝟏,𝟐,𝟑,𝟒}和4名单身女性{𝑨,𝑩,𝑪,𝑫},他(她)们的、爱慕序列如表8.9所示
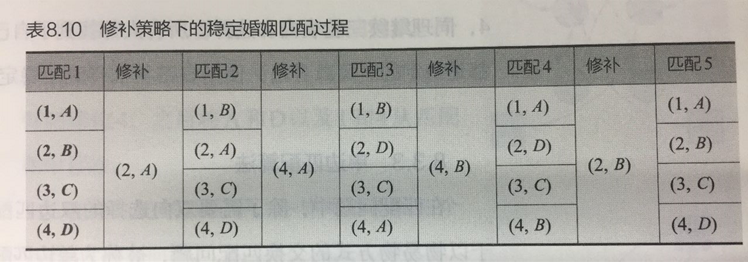
按照“修补”策略,匹配和修补过程如下
7.3.2.2 双边匹配问题:G-S算法
算法过程:
- 单身男性向最喜欢的女性表白
- 所有收到表白的女性从向其表白男性中选择最喜欢的男性,暂时匹配
- 未匹配的男性继续向没有拒绝过他的女性表白
- 收到表白的女性如果没有完成匹配,则从这一批表白者中选择最喜欢男性。即使收到表白的女性已经完成匹配,但是如果她认为有她更喜欢的男性,则可以拒绝之前的匹配者,重新匹配
- 如此循环迭代,直到所有人都成功匹配为止
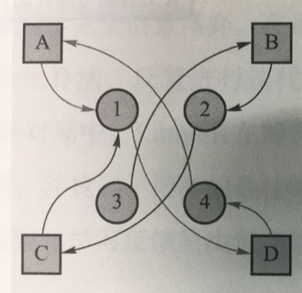
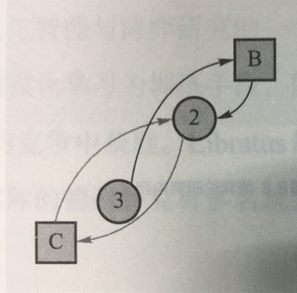
- 在第一轮中,4名男性分别向自己最喜欢的女性告白,而收到3人告白的女性𝐴选择了自己最喜欢的男性3,另一个收到告白的女性𝐵选择了男性4
- 在第二轮中,尚未匹配的男性1和男性2继续向自己第二喜欢的对象告白,收到告白的女性𝐵选择了自己更喜欢的男性2而放弃了男性4
- 同理继续三轮告白和选择,所有人都找到了自己的伴侣,且所有匹配都是稳定的
- 可以看出,使用G-S算法得到了稳定匹配的结果。
7.3.3 单边匹配问题:最大交易圈算法 Top-trading cycle TTC
算法流程:
- 首先记录每个物品的初始占有者,或者对物品进行随机分配
- 每个交易者连接一条指向他最喜欢的物品的边,并从每一个物品连接到其占有者或是具有高优先权的交易者
- 此时形成一张有向图,且必存在环,这种环被称为“交易圈”,对于交易圈中的交易者,将每人指向节点所代表的物品赋予交易者,同时交易者放弃原先占有的物品,占有者和匹配成功的物品离开匹配市场
- 接着从剩余的交易者和物品之间重复进行交易圈匹配,直到无法形成交易圈,算法停止
稳定室友匹配问题就是一个典型的单边匹配问题
假设某寝室有A、B、C、D四位同学和1、2、3、4四个床位,当前给A、B、C、D四位同学随机分配4、3、2、1四个床位
第一轮单边匹配:A和D之间构成一个交易圈,可达成交易,所以A得到床位1,D得到床位4,之后将 A和D以及1和4从匹配图中移除
第二轮单边匹配:B和C都希望得到床位2,无法再构成交易圈,但是由于C是床位的本身拥有者,所以C仍然得到床位2,B只能选择床位3
最后交易结果A→1,B →3,C →2,D →4
7.4 非完全信息博弈的实际应用
7.4.1 博弈论研究内容
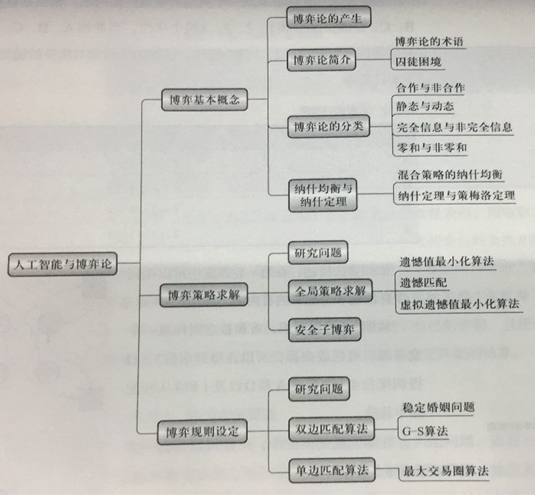
7.4.2 求解非完全信息博弈纳什均衡的一般方法
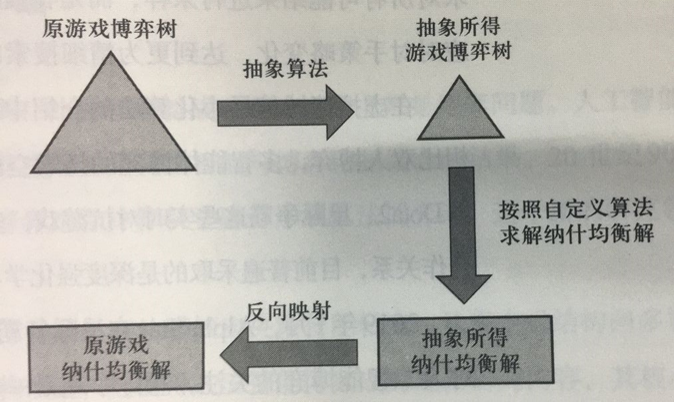
7.4.3 与深度强化学习相结合