八、动画：动画技术基础

8.1 2D游戏动画技术

8.1.1 Sprite Animation

记录每一帧的动作，循环播放

image-20230725172639259

在不同视角采样一系列的动作，根据当前视角播放不同动画

image-20230725173034724

现代游戏引擎中，粒子效果就是Sprite Animation

image-20230725173149954

8.1.2 Live2D

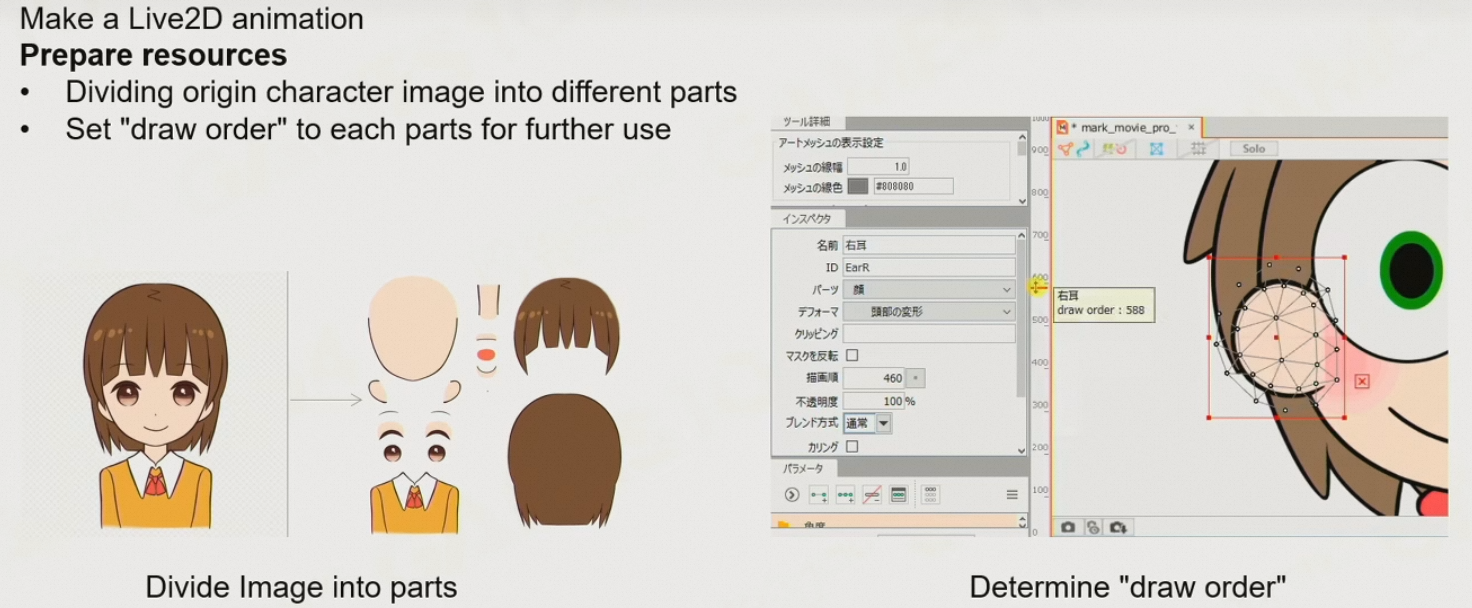
将一个角色的所有元素，变成一个个小图元，通过变换图元，组成人物的不同姿态

image-20230725173218195

image-20230725173430996

  1. 首先，定义不同图元的深度，以控制图元是否出现，不同图元之间的层次关系

    image-20230725173813825

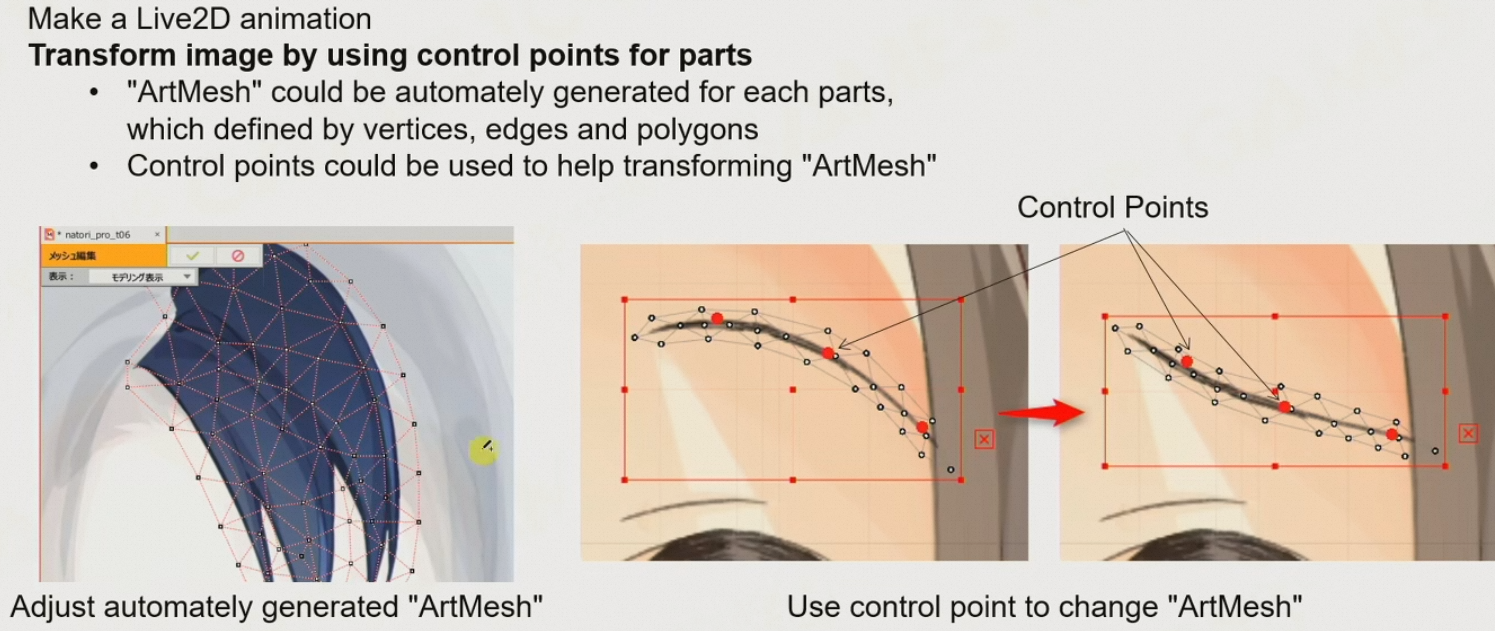
  2. 然后，生成ArtMesh，通过拖动ArtMesh上的控制点，控制图元的变化

    image-20230725173852827

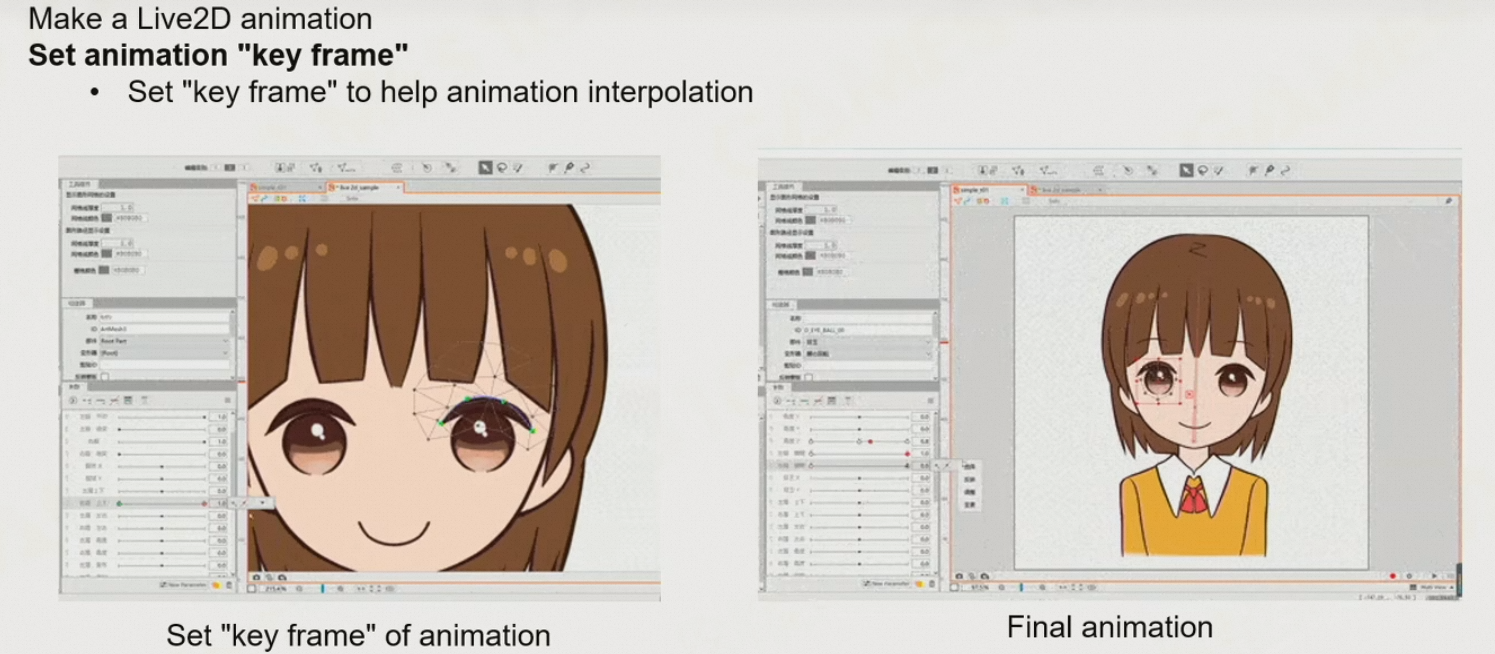
  3. 设置动画关键帧，从而进行动画插值

    image-20230725173944369

8.2 3D游戏动画技术

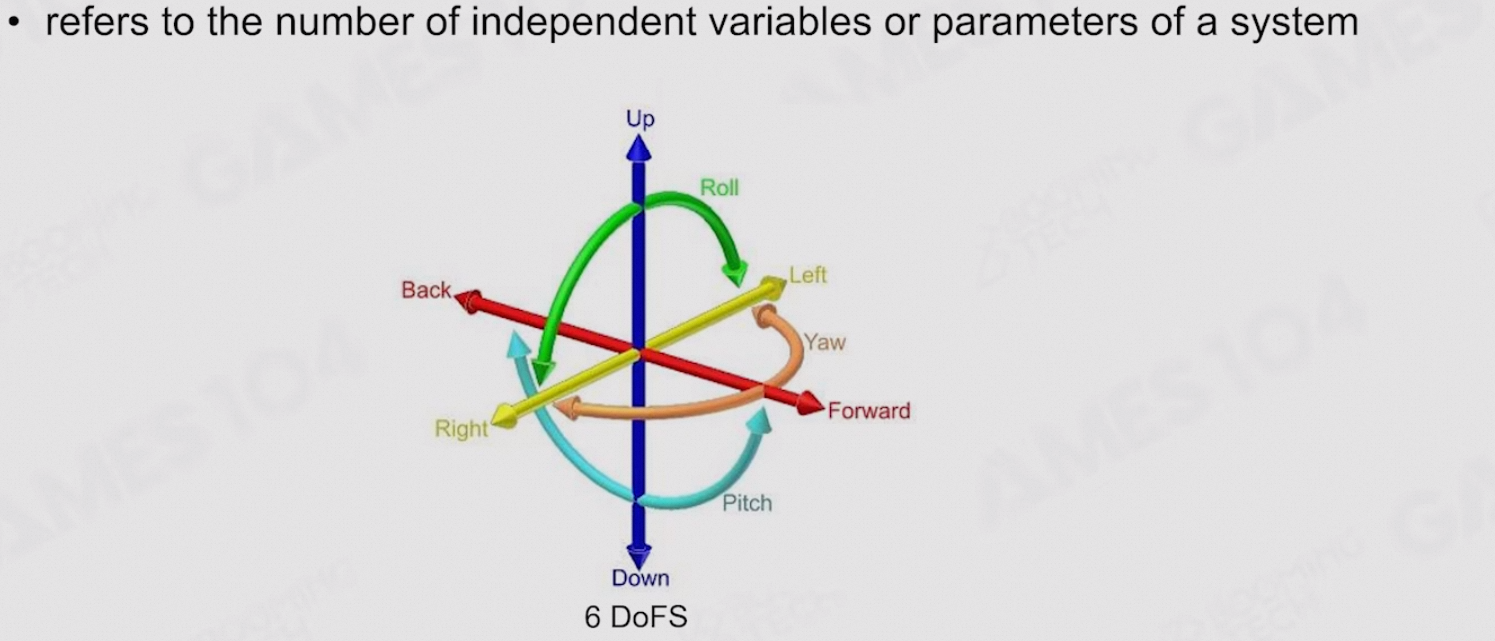
8.2.1 DoF：Degress of Freedom 自由度

一个物体可以在多少个维度进行变化

  1. 刚体：6个自由度，平移3个，旋转3个

image-20230725174149918

8.2.2 Rigid Hierarchical Animation

  1. 将mesh分为层次化的多个可以变化的刚体，动画即是改变这些刚体的平移/旋转
  2. 缺点：不同关节之间可能会穿插

image-20230725174416495

8.2.3 Per-vertex Animation 顶点动画

顶点动画：

  1. 记录每个顶点的位置随时间的变化
  2. 一般存两个texture，一个texture记录顶点的位置，另一个记录顶点的法向
  3. 通常是用物理引擎离线计算好，然后存到texture中

image-20230725174558034

8.2.4 Morph Target Animation

  1. 也是一种顶点动画，但是记录的是顶点影响权重
  2. 存储多个Key Poses，然后在Key Poses之间进行插值
  3. 在捏脸系统中更好用

image-20230725174900318

8.2.5 Skinned Animation 蒙皮动画

刚体骨骼驱动外表的蒙皮进行动画，每个顶点由多个骨骼同时影响

image-20230725175213453

image-20230725175347643

8.2.6 Physics-based Animation

  1. 布娃娃系统
  2. 衣料、流体模拟
  3. IK反向动力学

image-20230725175428162

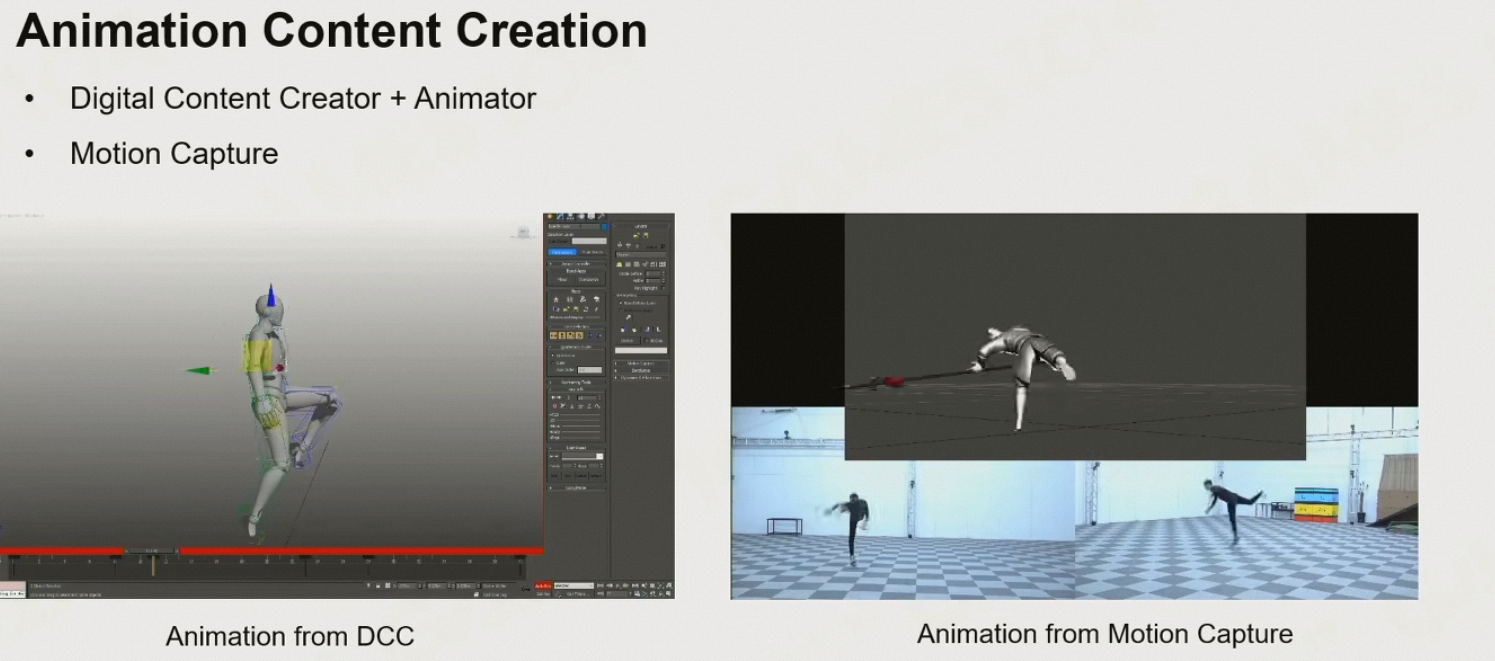
8.2.7 Animation Content Creation

  1. 动画师设置关键帧
  2. 动捕

image-20230725175649795

8.3 蒙皮动画的实现

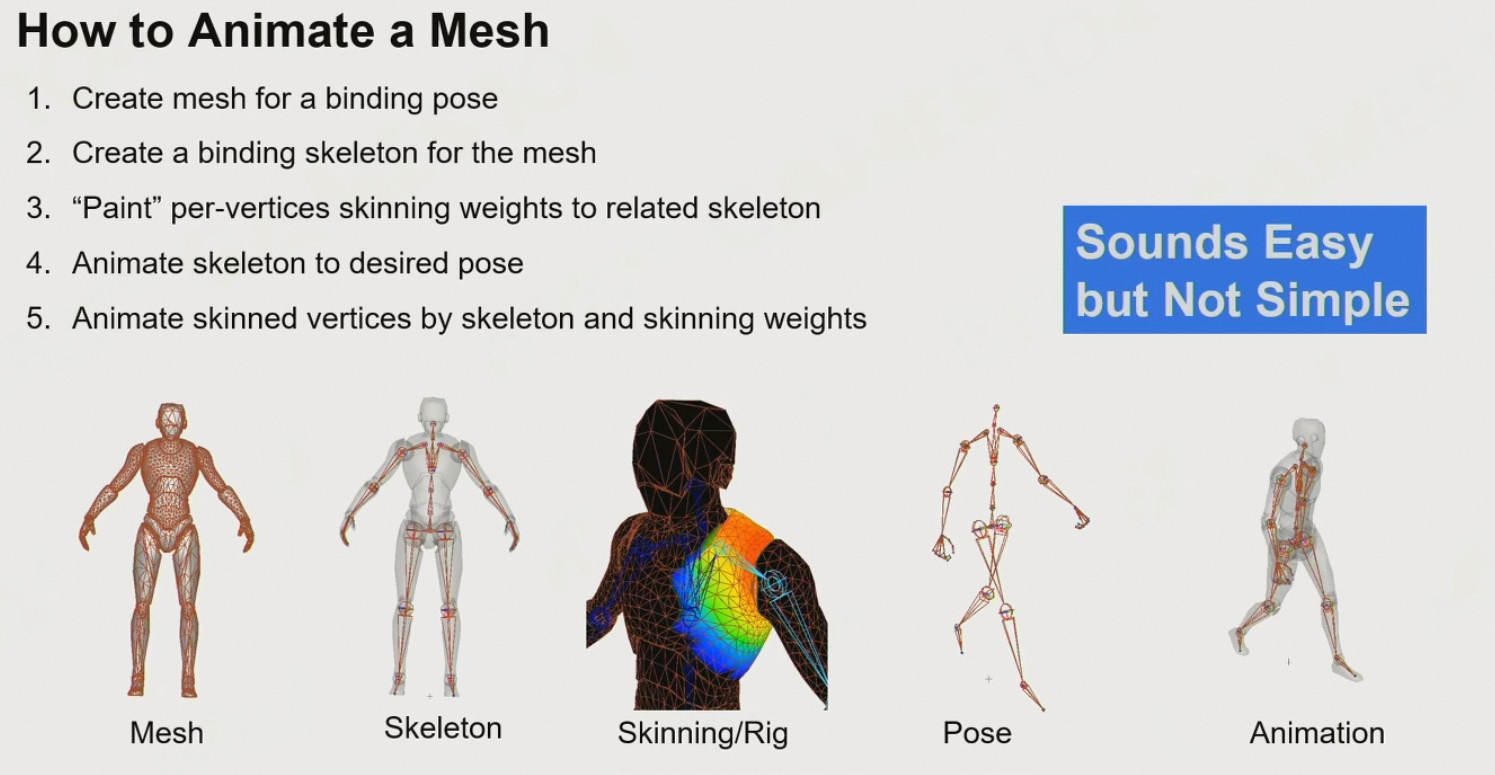
8.3.1 如何让Mesh播放动画

  1. 创建mesh的binding pose
  2. 创建binding skeleton
  3. 刷上蒙皮，告诉每个顶点应该受到哪些骨骼的影响
  4. 移动skeleton
  5. 蒙皮上的顶点会跟着运动

image-20230726102514399

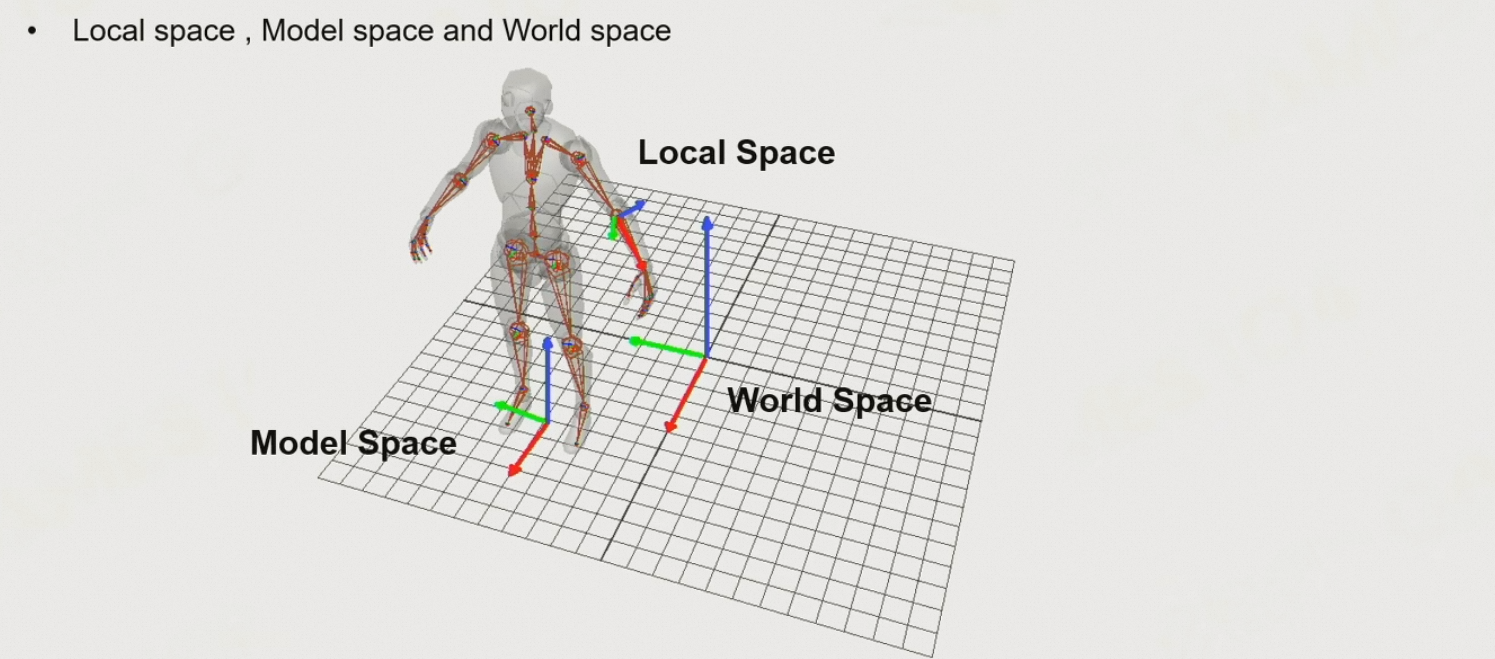
8.3.2 不同的空间

  1. 世界空间：全局坐标系
  2. 模型空间：以角色为中心，相对世界空间有平移&旋转
  3. 局部空间：每根骨骼的坐标系，每根骨骼都不相同，需要逐步累加进来

image-20230726102748726

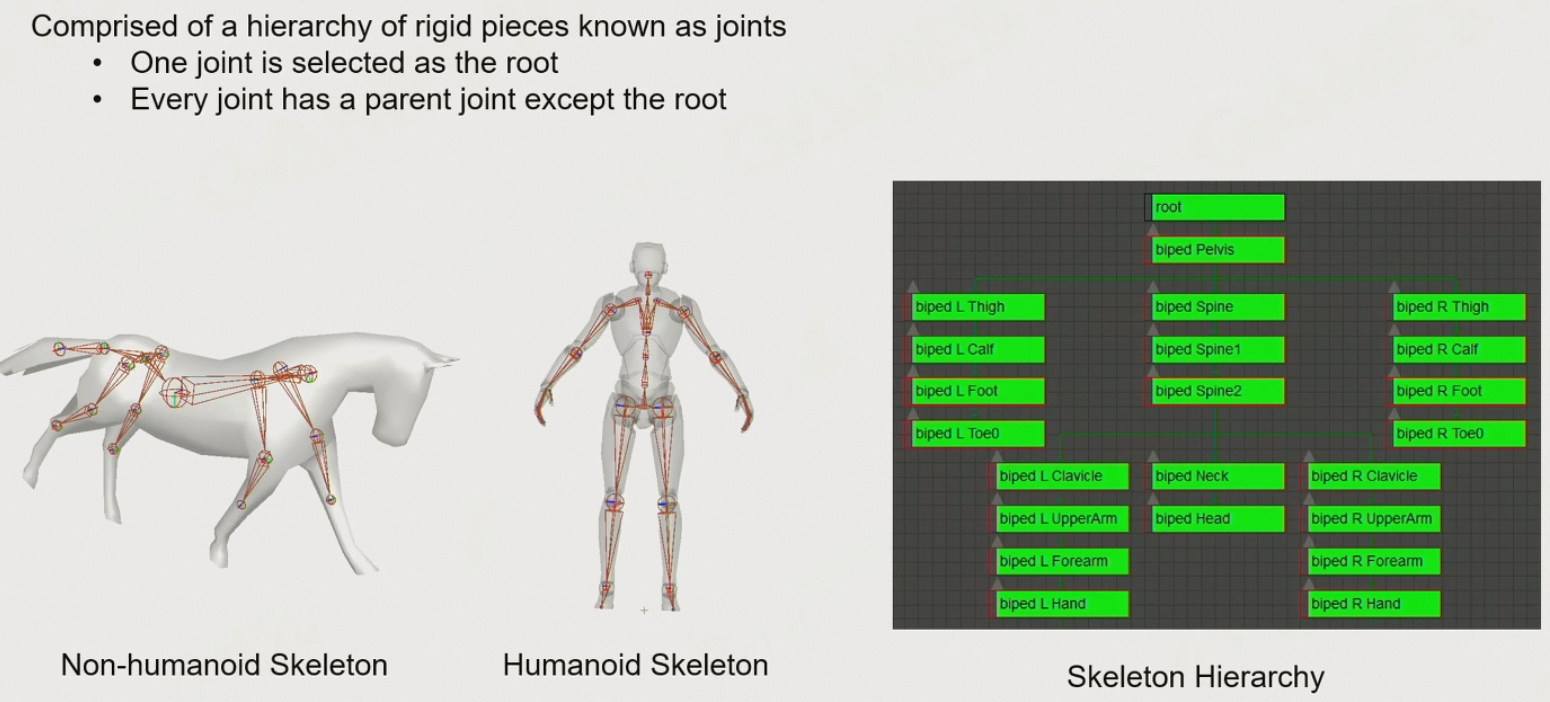
8.3.3 两种骨骼

Humanoid Skeleton：两足动物的骨骼

  1. 起点在人的胯部：Pelvis
  2. 有时会在Pelvis之上添加一个root

Non-humanoid Skeleton：四足动物的骨骼

image-20230726103147477

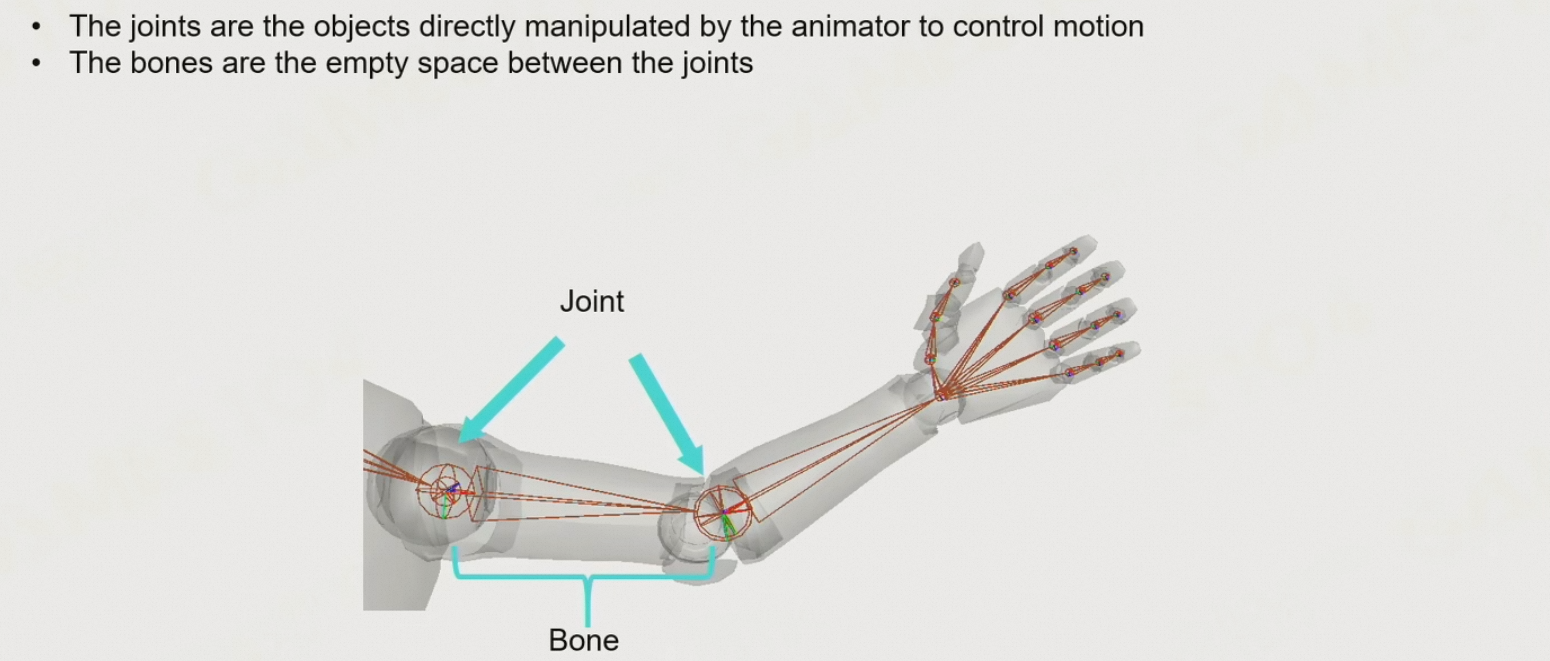
8.3.4 骨骼 Bone & 关节 Joint

  1. 在引擎中，存储的是关节的信息
  2. 相邻两个关节定义一个骨骼
  3. joint是严格的刚体，无法被扭曲；而bone是可以扭曲的

image-20230726103450456

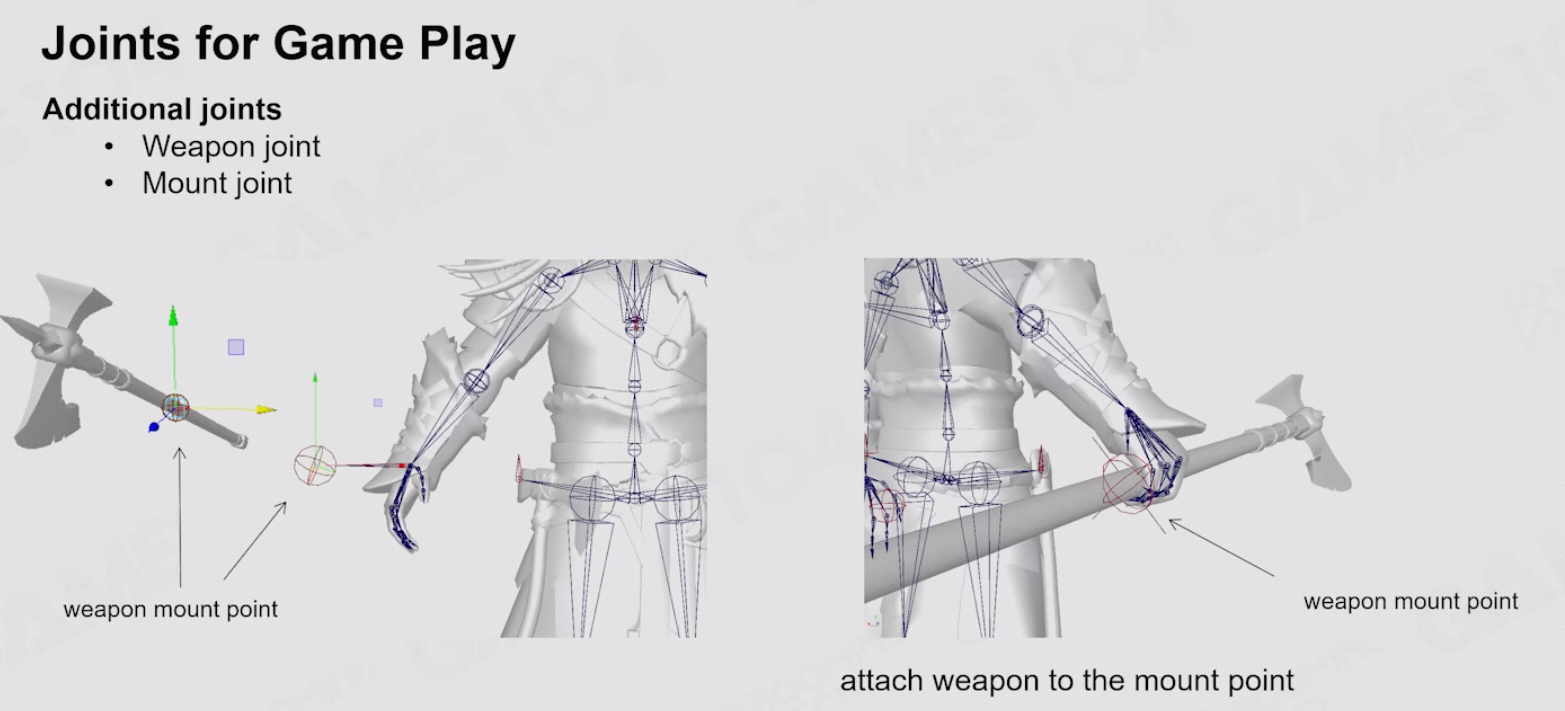
8.3.5 游戏中的关节

  1. 通常会添加一些额外的骨骼，用于控制角色的面部表情、衣物等附加物
  2. 武器、骑乘等都会有对应的关节，用于绑定外部物品

image-20230726103902491

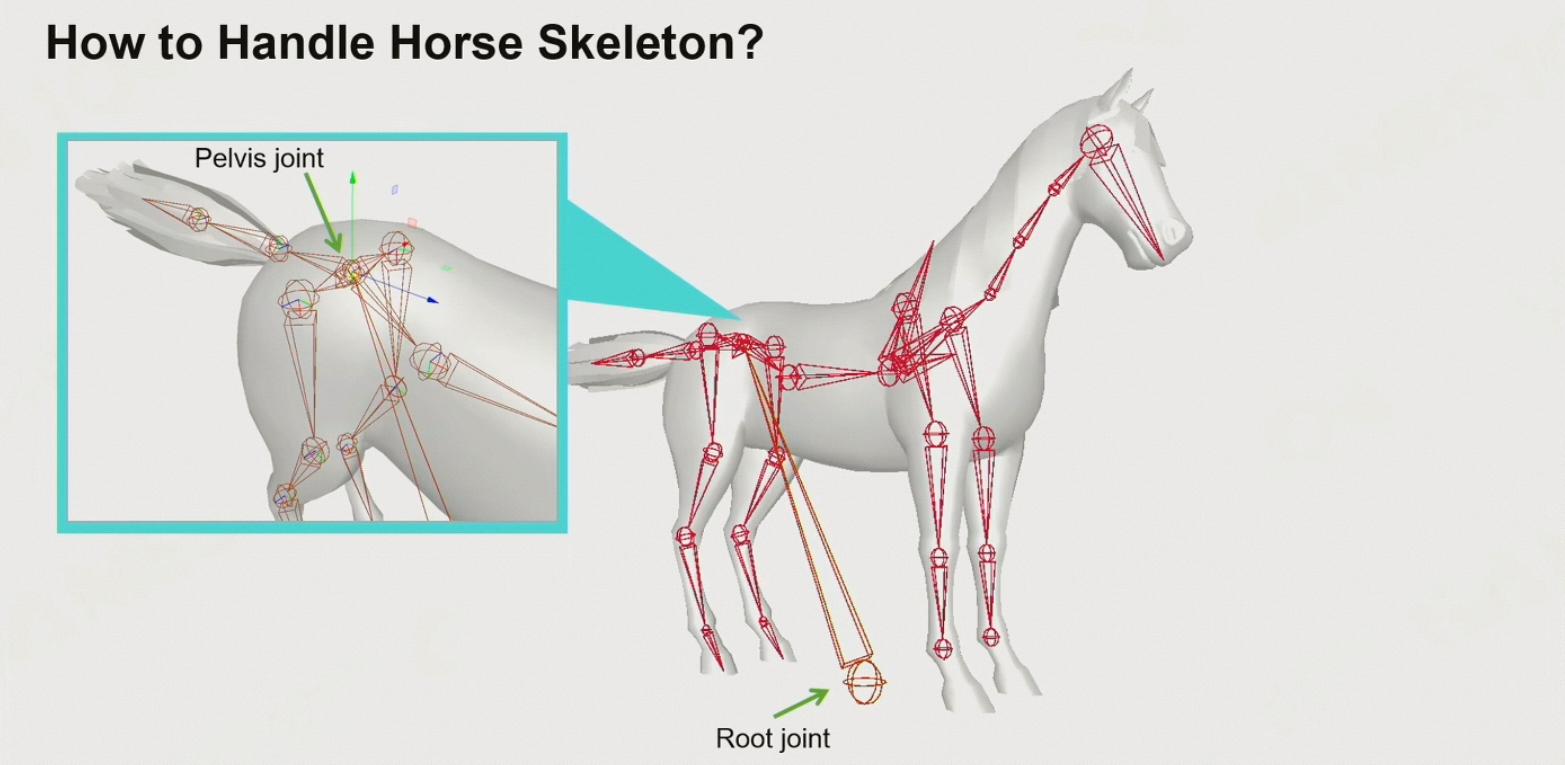
8.3.6 根骨骼

  1. 通常会放置于两脚之间，便于表示离地高度、移速等属性

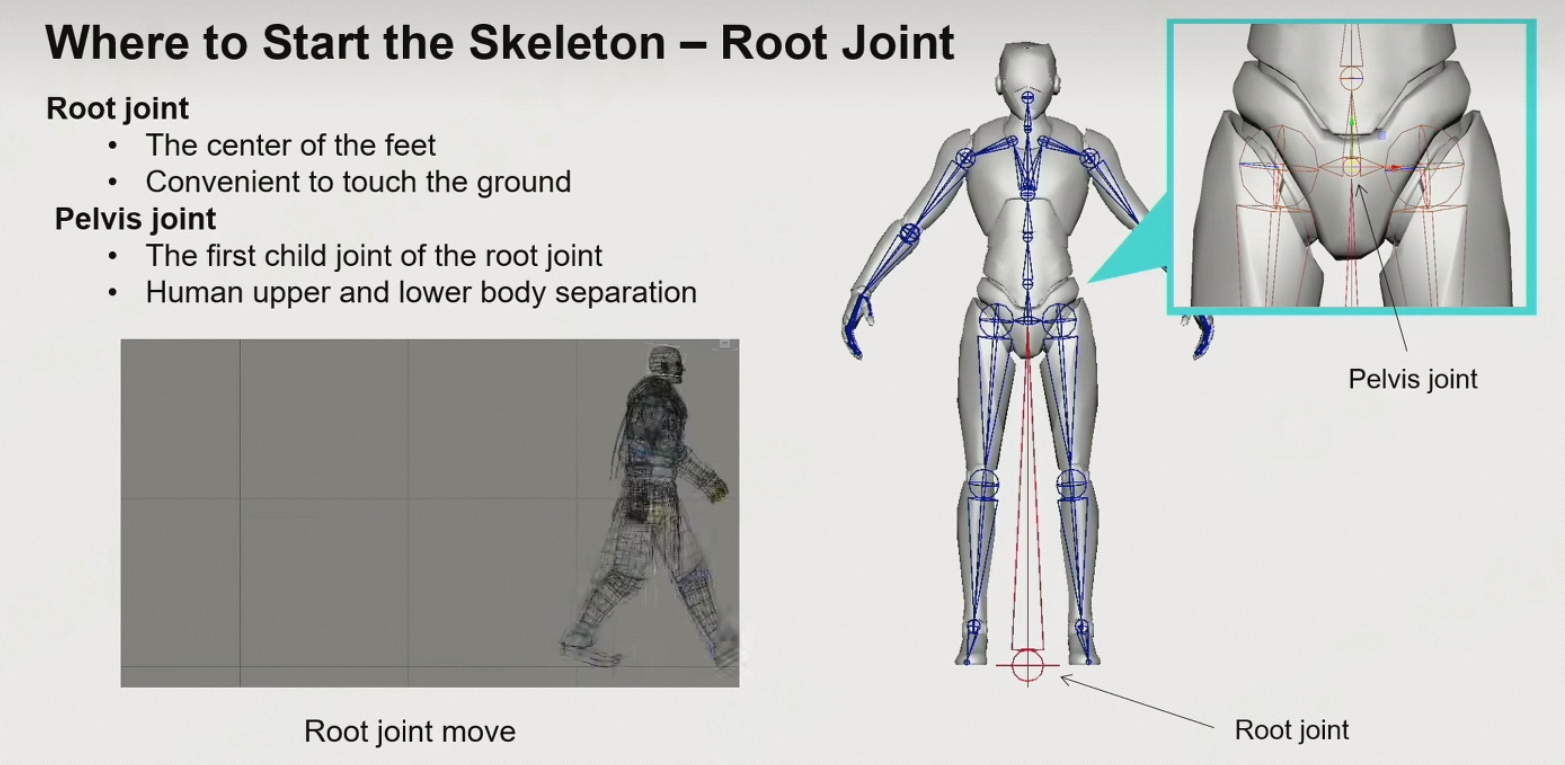
image-20230726104007356

  1. 四足动物的Pelvis在尾椎处，而root在肚子下四足中心

image-20230726104125333

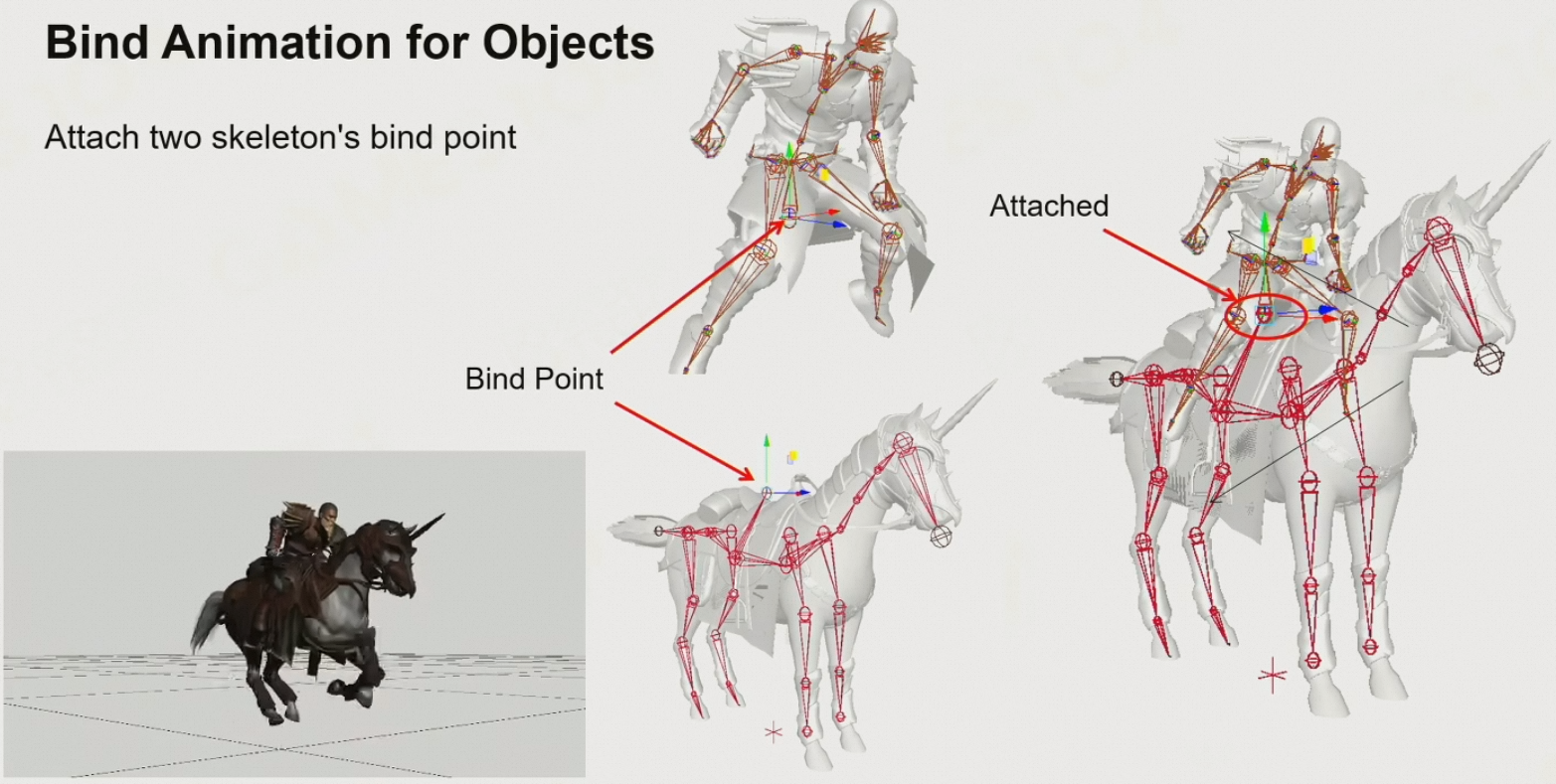
8.3.7 绑定动画

  1. 当人物骑乘在马身上时，两者的bind point就会绑定到一起
    1. 不仅仅是位置的绑定，还有旋转的绑定
  2. 两者分别播放自己的动画

image-20230726104219332

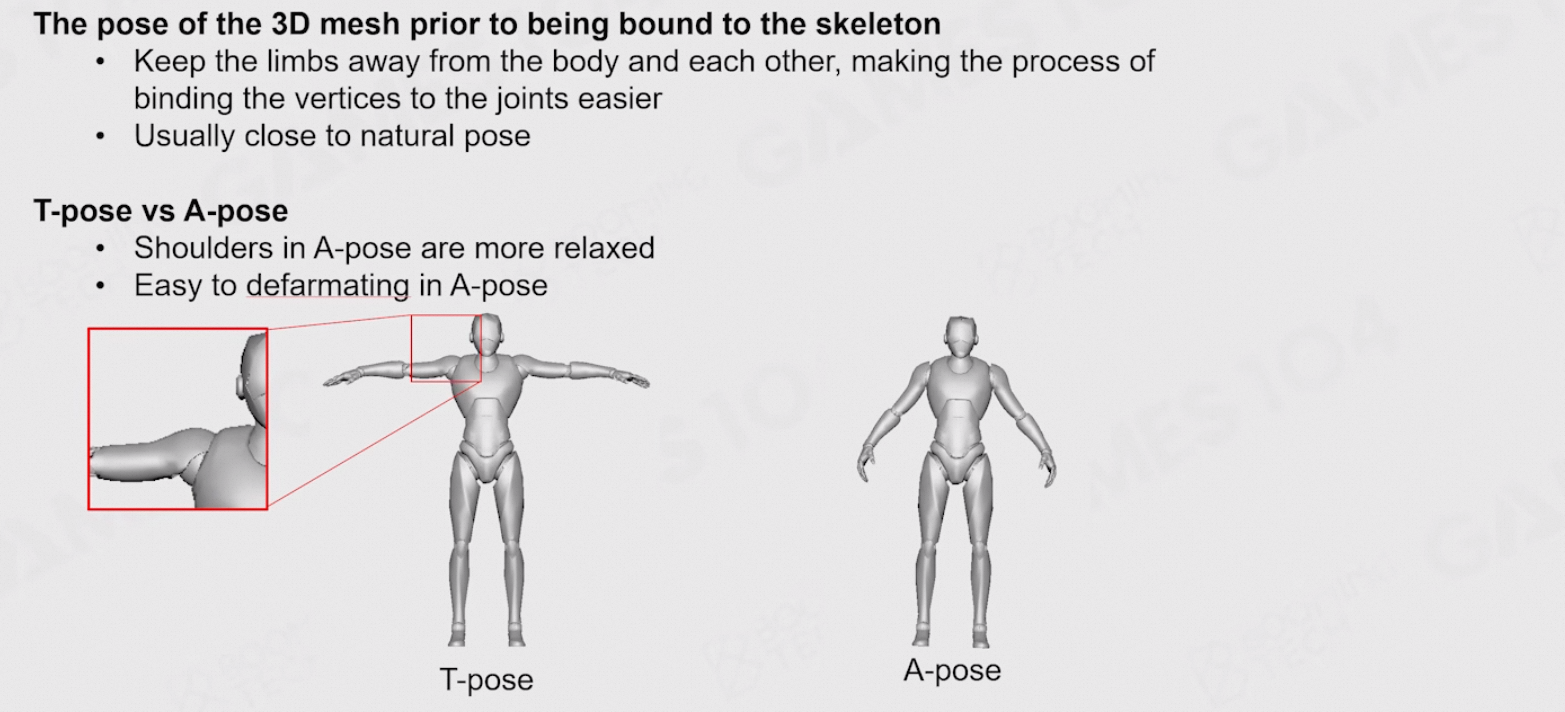
8.3.8 绑定姿势：T-pose vs A-pose

T-pose：肩胛处的骨骼是压缩的，精度不够

A-pose：人相对自然的站在那里，肩胛处的精度会更高

image-20230726104519860

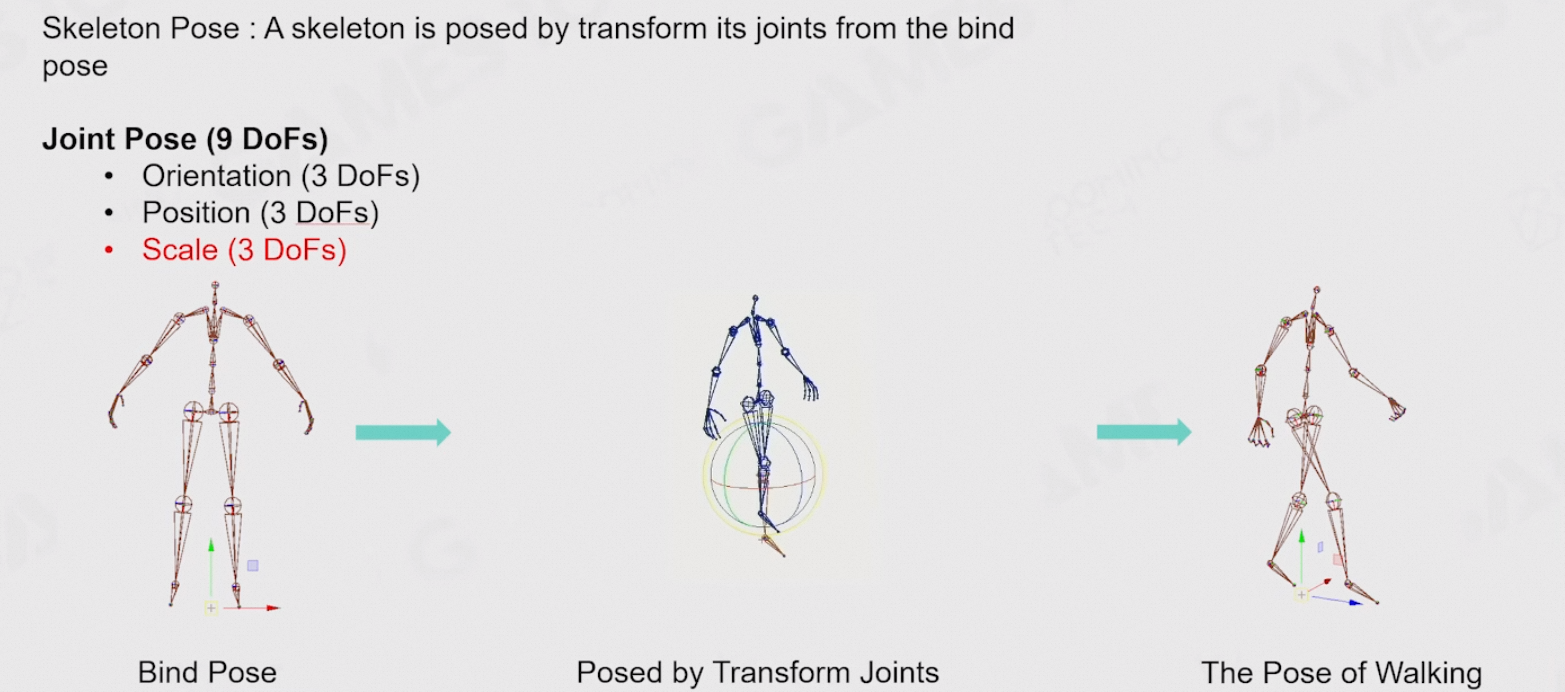
8.3.9 骨骼姿势

关节姿势有9个自由度：平移、旋转、缩放

image-20230726104647937

8.4 3D旋转的数学原理

8.4.1 2D空间的旋转

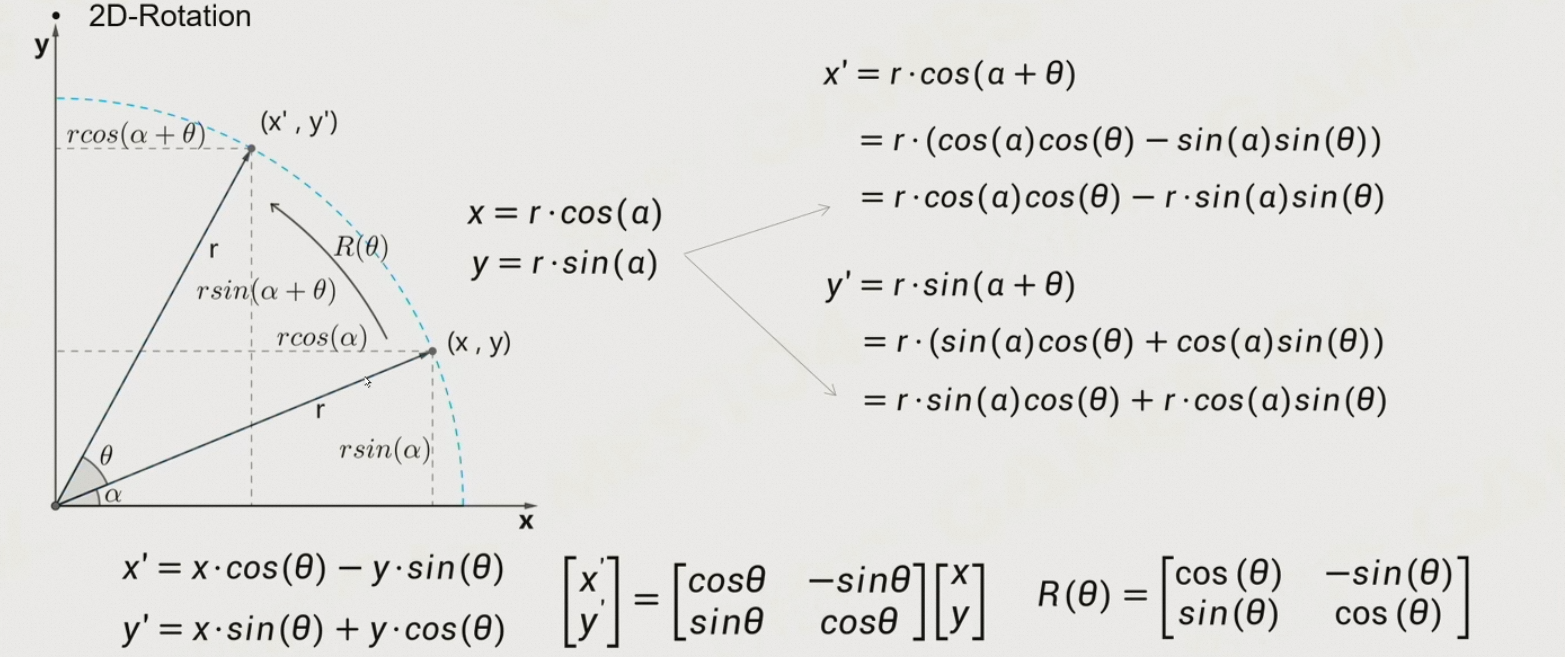
image-20230726104902602

8.4.2 3D空间的旋转：欧拉角

8.4.2.1 旋转矩阵

image-20230726105052981

8.4.2.2 Yaw & Pitch & Roll

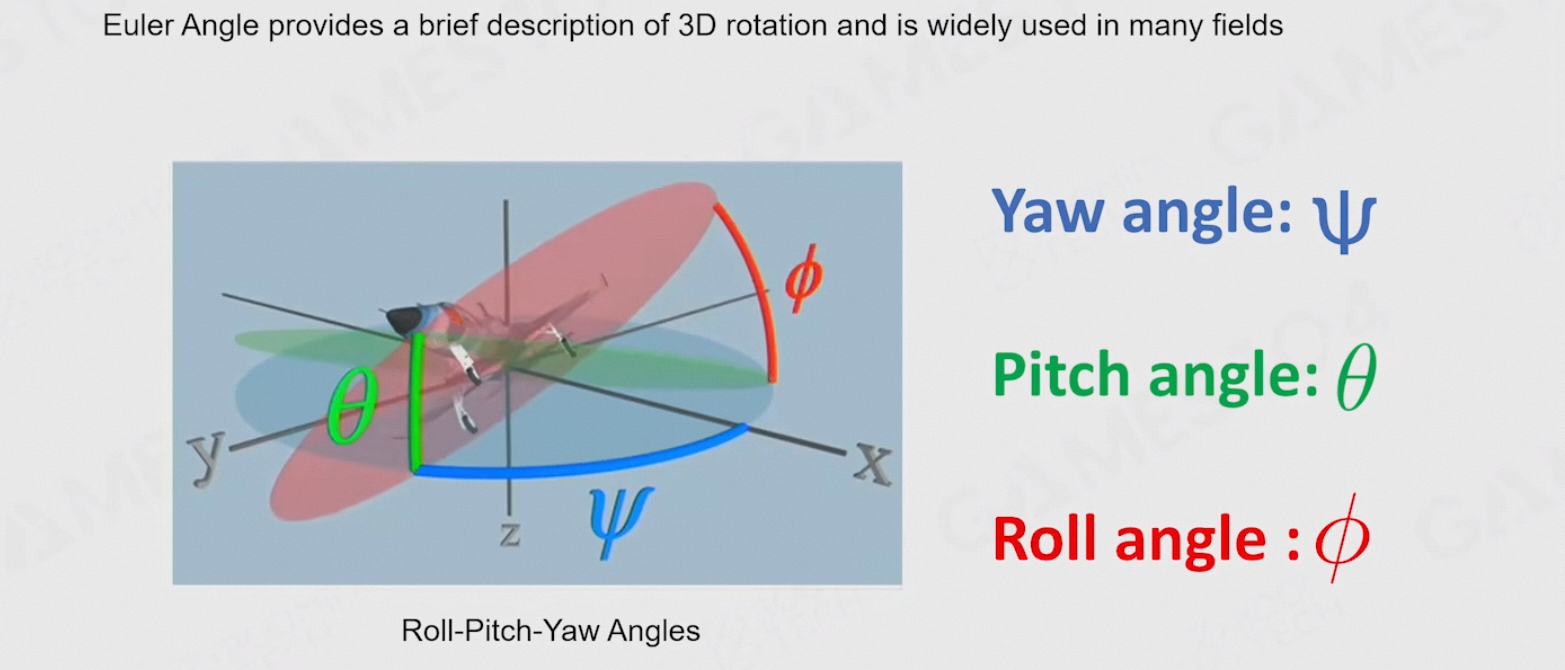
image-20230726105207538

8.4.2.3 问题：欧拉角的运算是严格依赖顺序的

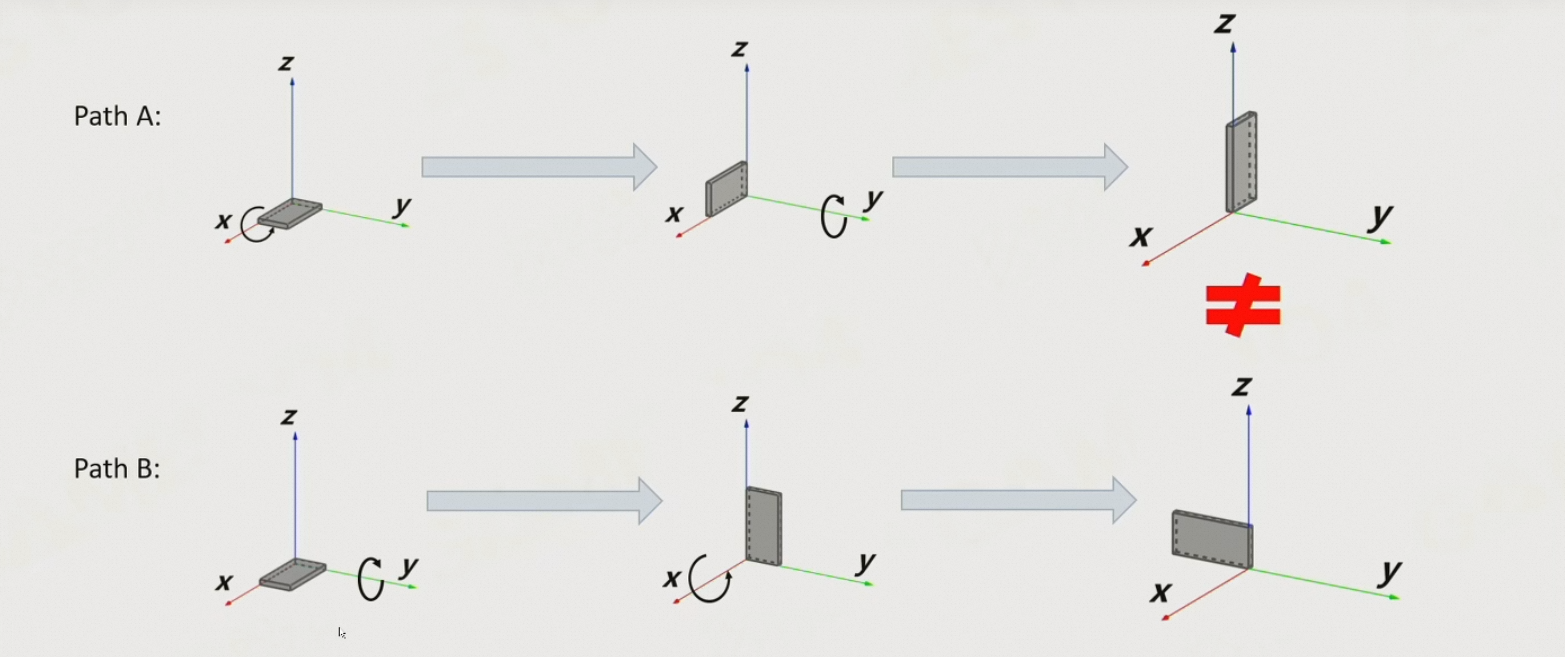
image-20230726105341930

8.4.2.4 万向锁：Gimbal lock

image-20230726105432867

8.4.2.5 欧拉角的退化现象：β=90°

当β=90°时，α和γ各自都没有意义，只有α-γ有意义，此时最终的DoF变为了1

image-20230726105811316

8.4.2.6 欧拉角的问题

  1. 万向锁
  2. 难以插值
  3. 难以进行旋转的叠加，必须通过旋转矩阵相乘
  4. 难以进行任意轴旋转，必须将其分解为XYZ轴的旋转

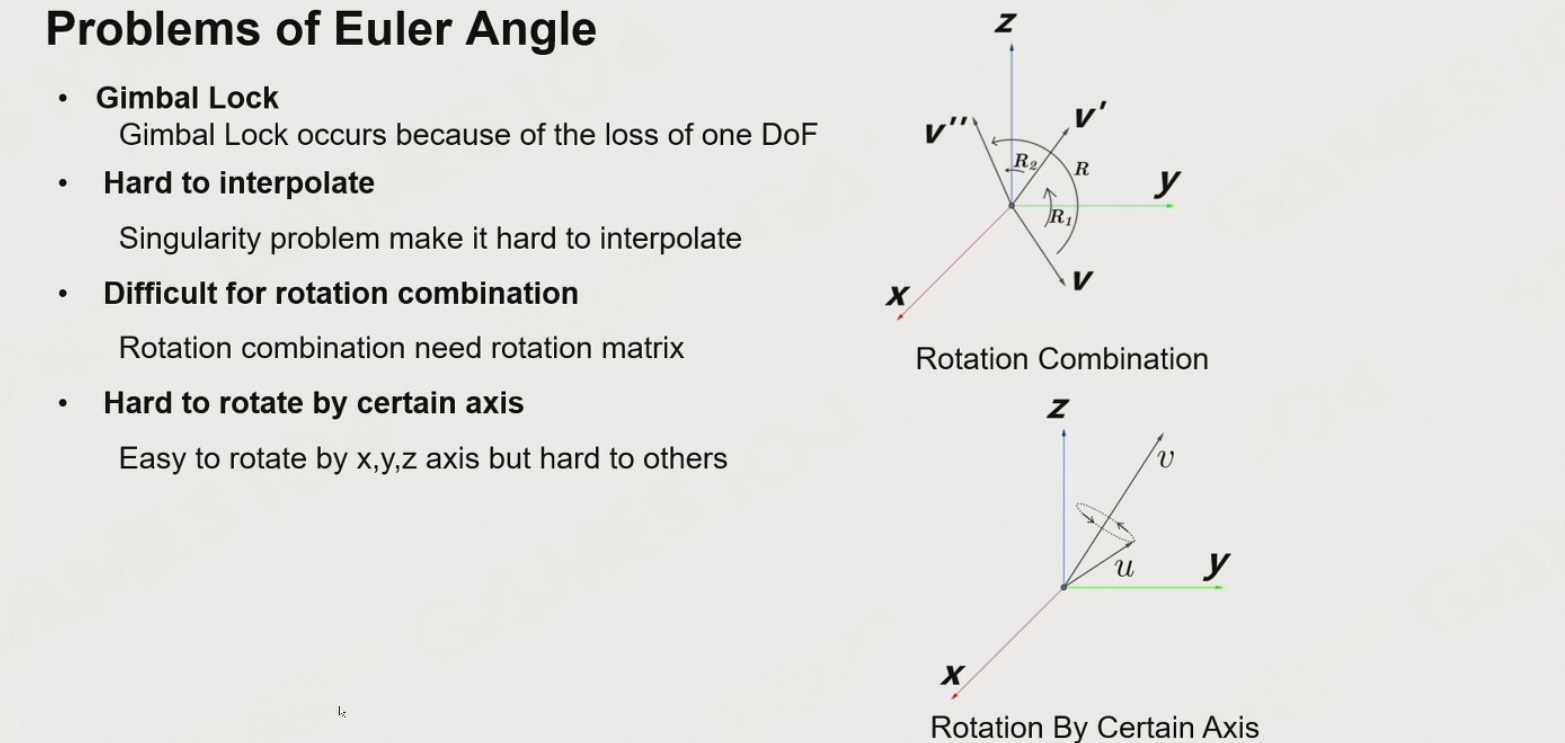
image-20230726105951500

8.4.3 四元数 Quaternion

8.4.3.1 用复数表示2D旋转

image-20230726110321992

8.4.3.2 四元数的定义

定义：\(q=a+bi+cj+dk \ (a,b,c,d\in R)\)，其中 \(i^2=j^2=k^2=ijk=-1\)

性质：单位四元数的共轭，就是它的逆

image-20230726115007887

8.4.3.3 欧拉角 => 四元数

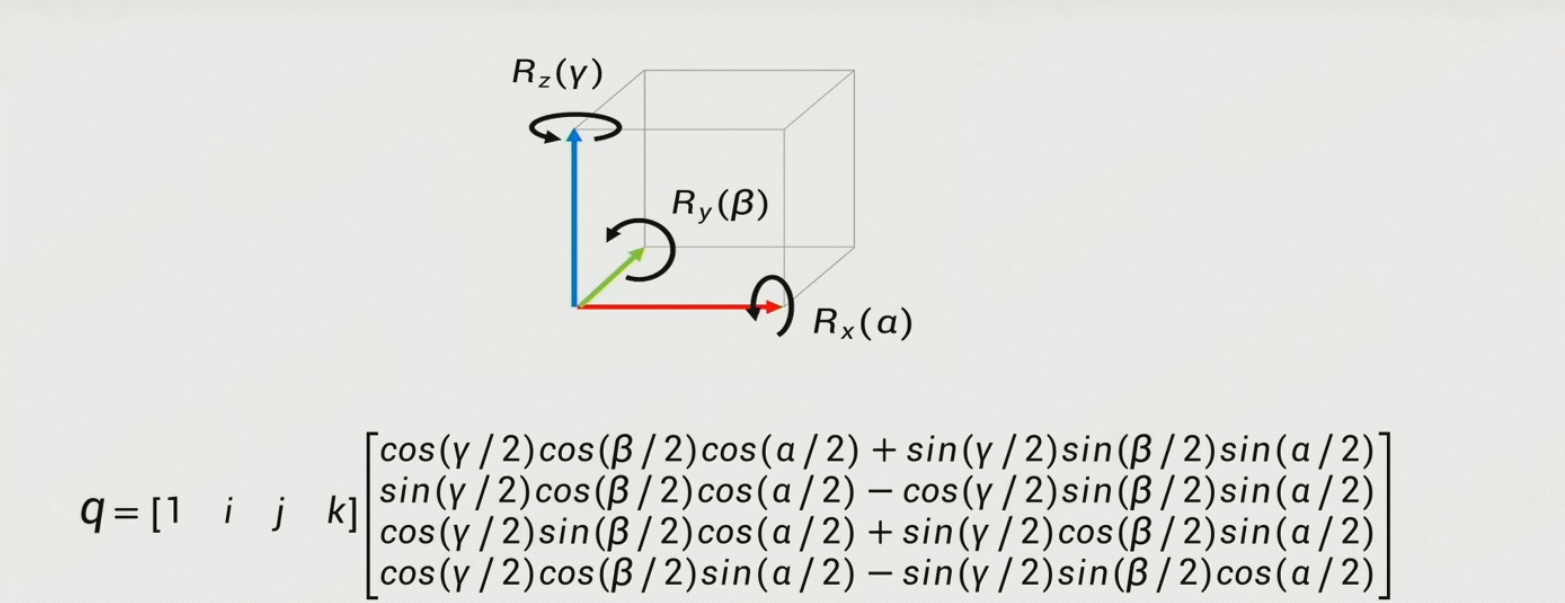
image-20230726111111068

8.4.3.4 用四元数表示旋转

image-20230726114919429

image-20230726115156359

image-20230726115332722

image-20230726140131693

8.5 关节与蒙皮

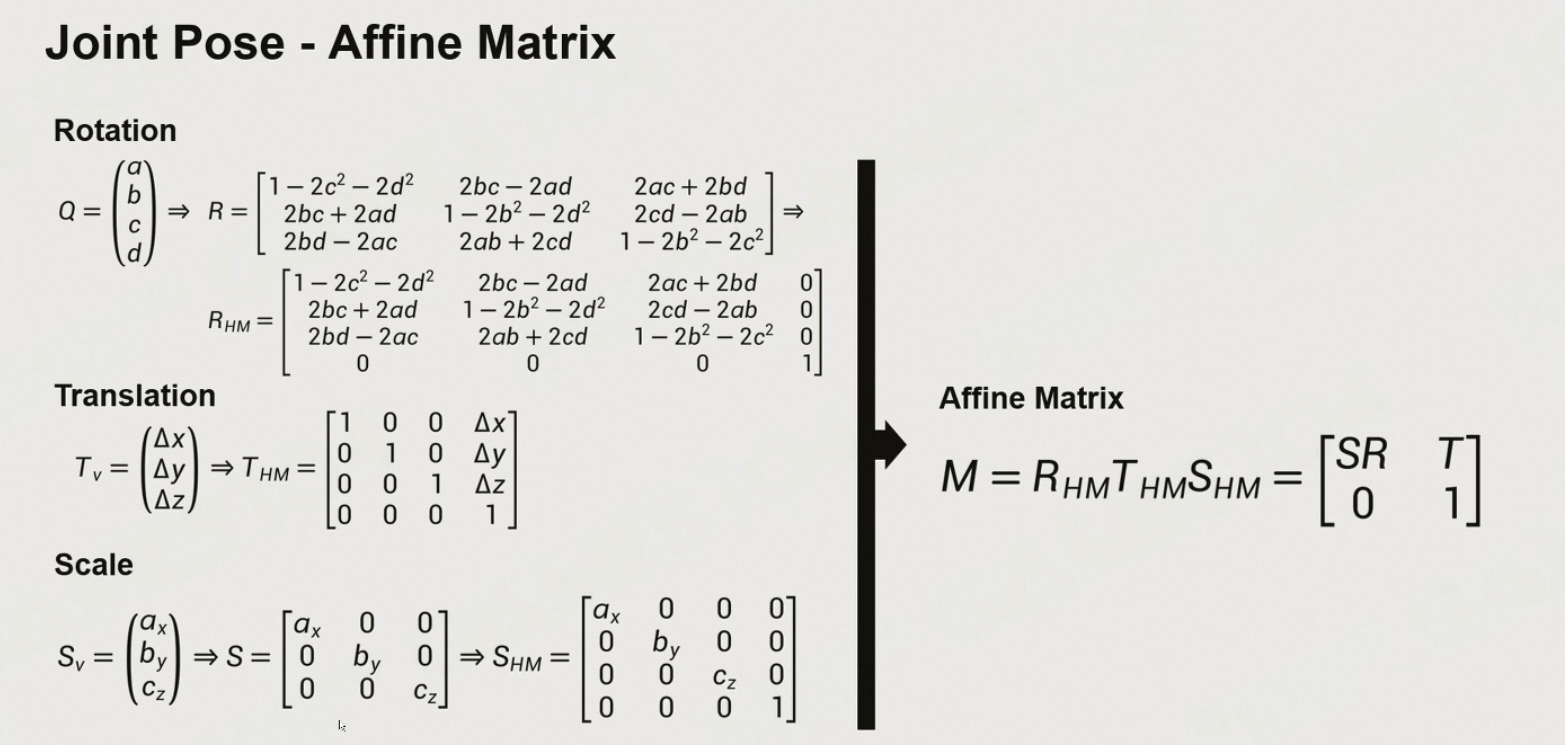
8.5.1 三种数据：旋转、平移、缩放

  1. Orientation 空间上的朝向

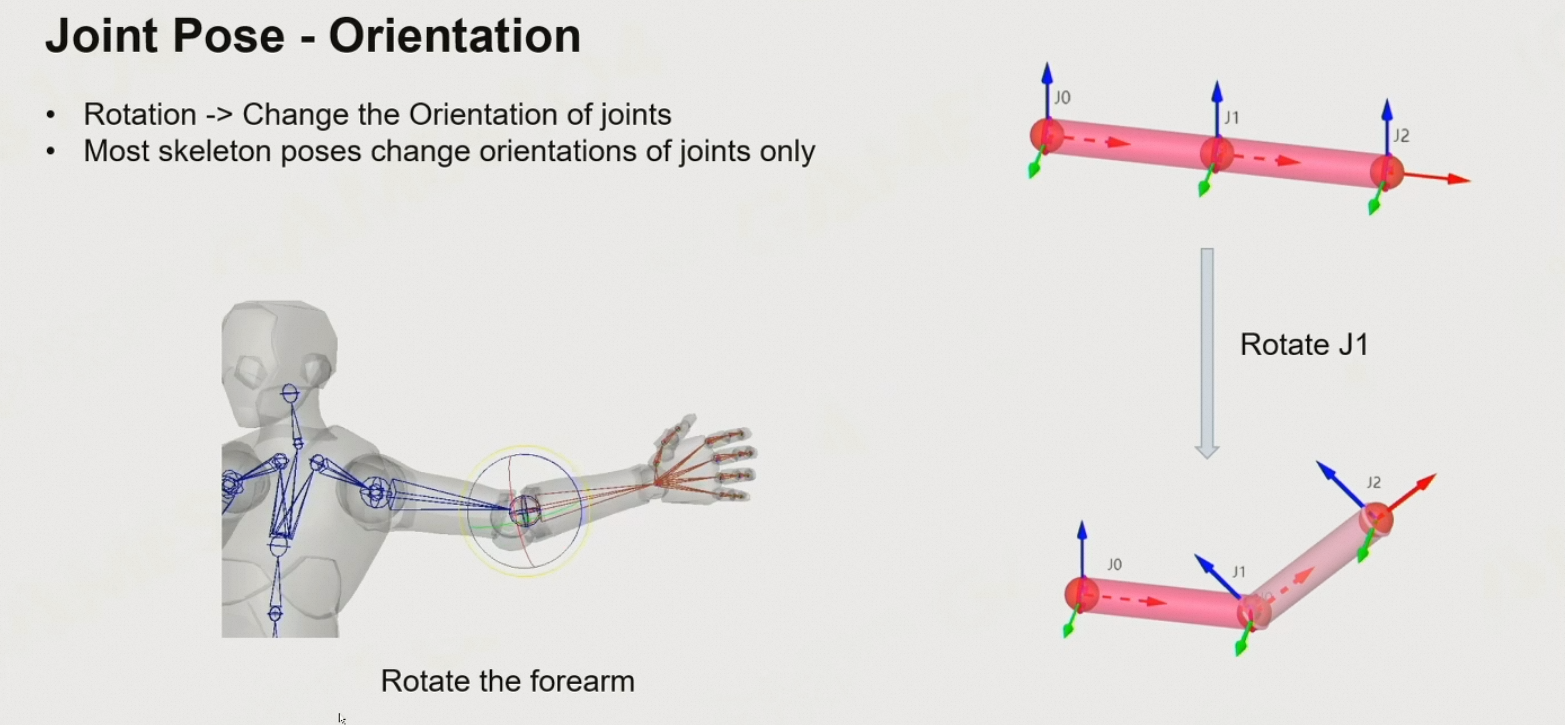
    image-20230726140531917

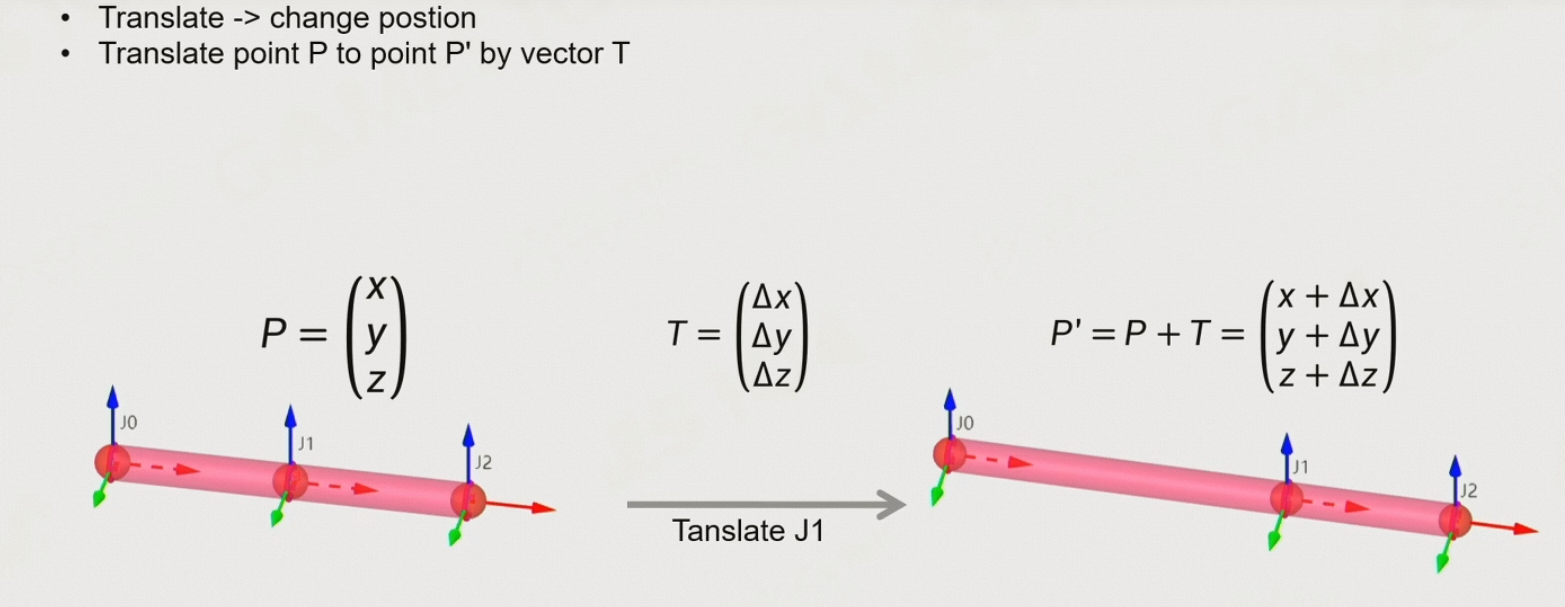
  2. Position

    1. 通常是不变的
    2. 但是当角色蹲下时，是通过pelvis相对于root的位置变换表示的
    3. 表情动画也会用到位置变换

    image-20230726140846380

    image-20230726141023444

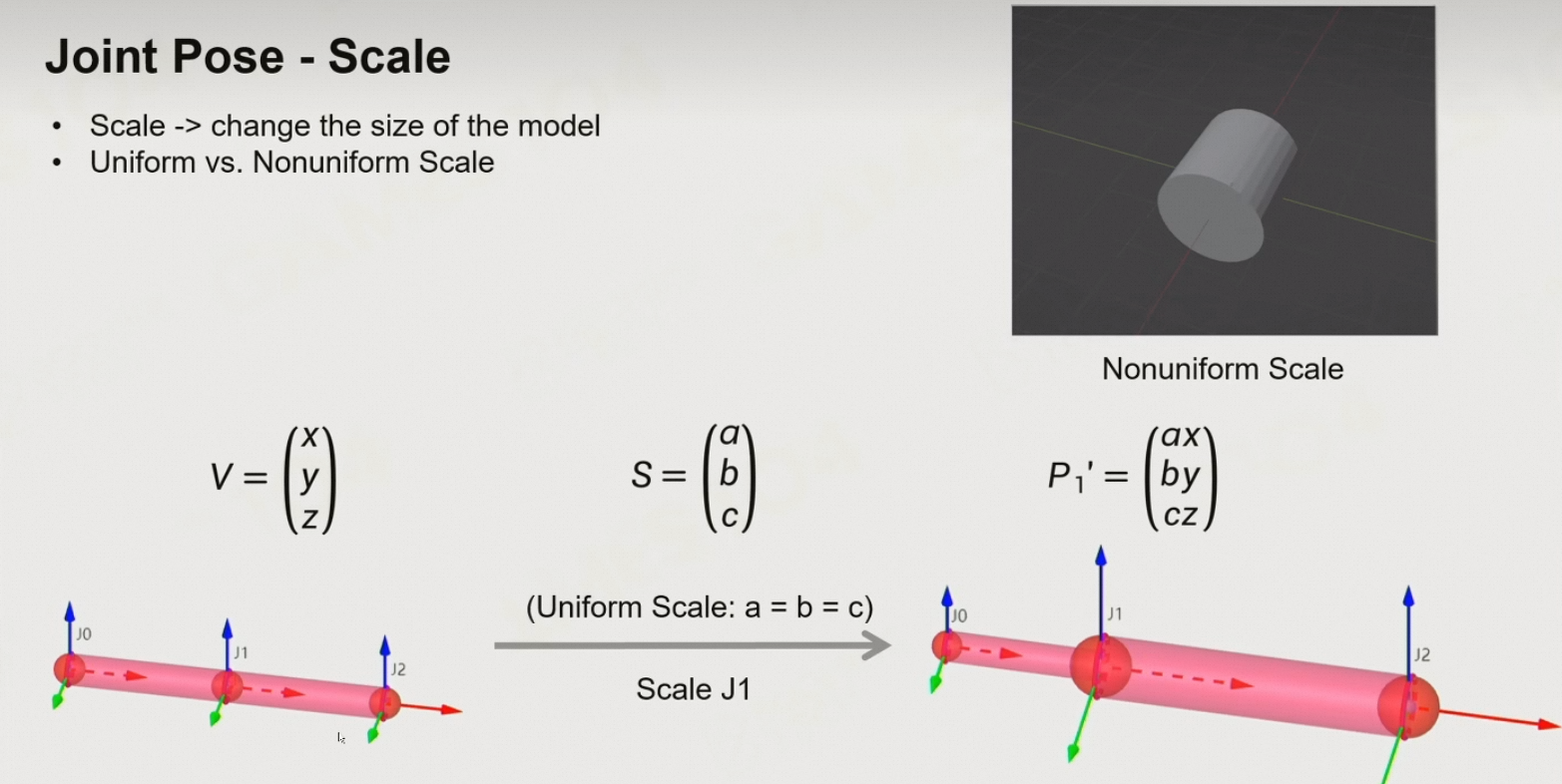
  3. Scale：缩放变换

    1. 通常也不会变
    2. 但是在更改角色面部关节时，可能会改变

    image-20230726141049396

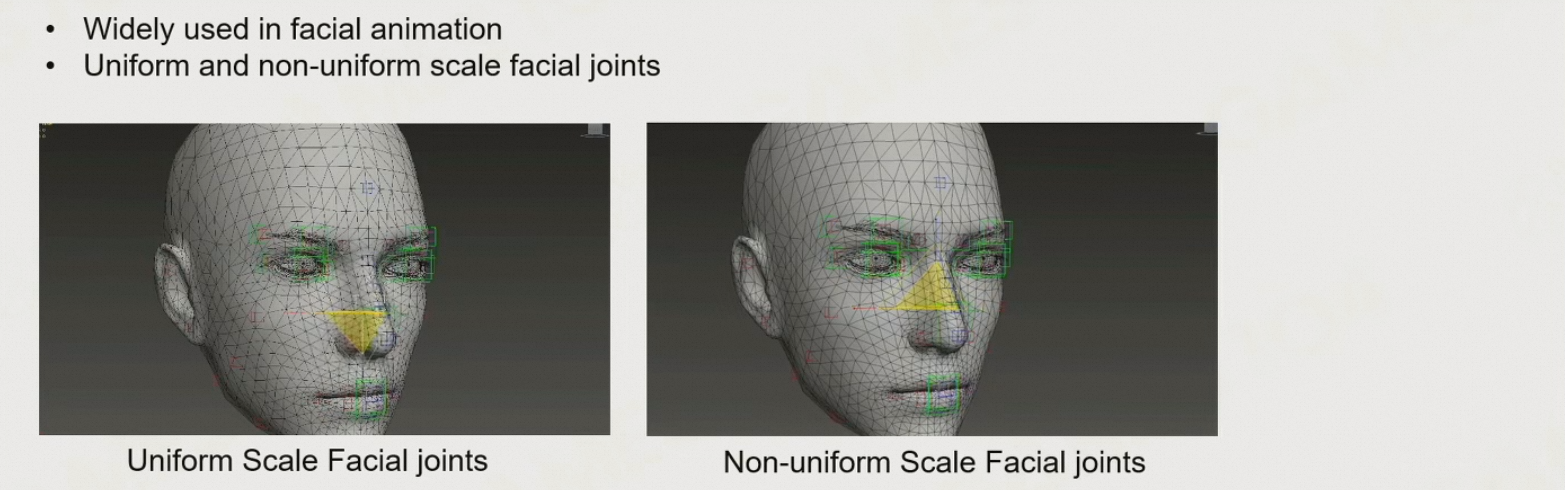
    image-20230726141102714

8.5.2 Affine Matrix 仿射矩阵

image-20230726141216420

8.5.3 局部空间 => 模型空间

对于每一个关节\(j\)：

  1. \(p(j)\)：父关节
  2. \(M_{p(j)}^l\)：父关节在局部空间的关节姿势
  3. \(M_j^m\)：关节在模型空间的关节姿势

\[ M_j^m=\prod_{j=J}^0 M_{p(j)}^l \]

即从当前节点开始，逐步乘父节点的关节姿势，直到到达根节点

image-20230726141439188

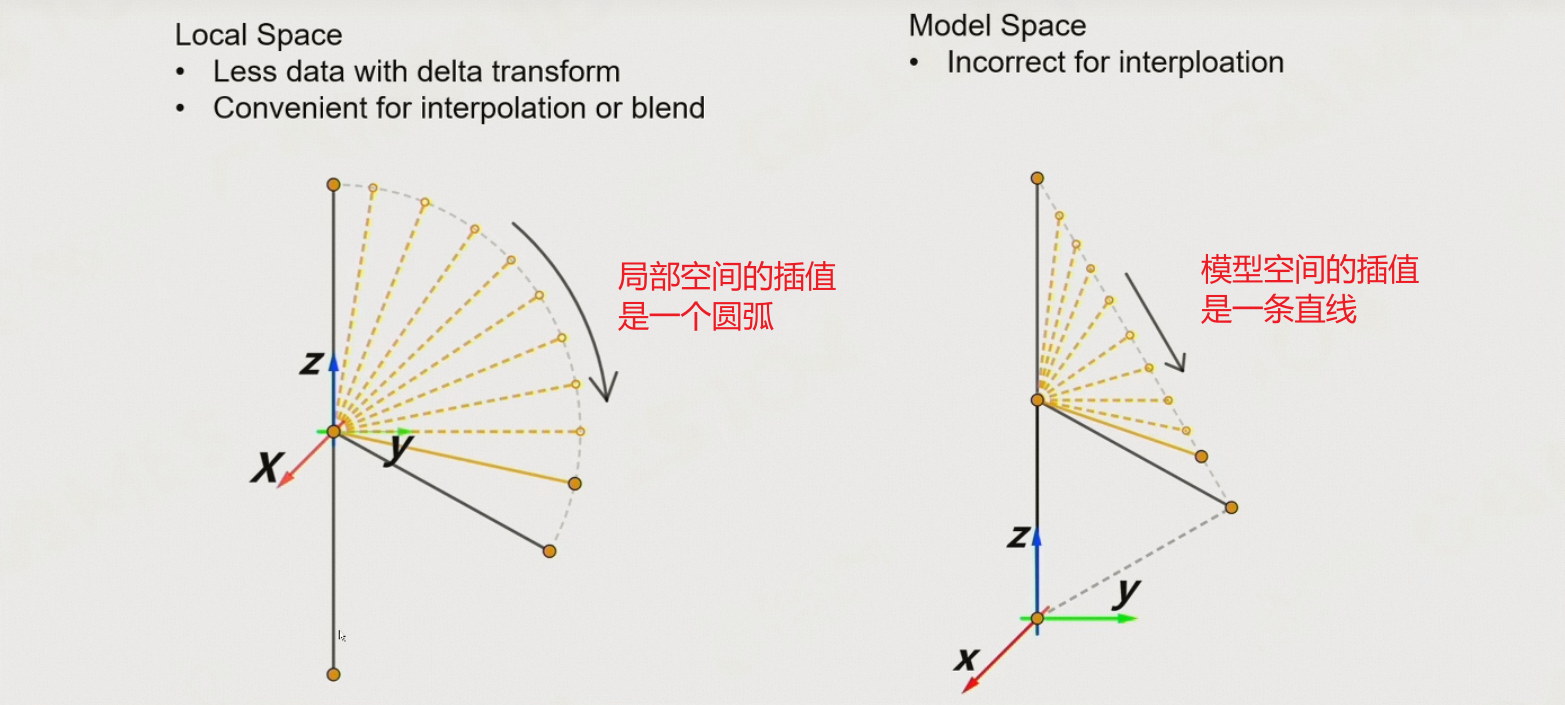
8.5.4 关节姿势的插值：局部空间 vs 模型空间

将动画存储在局部坐标系

  1. transform中的数据更少
  2. 更容易进行插值/混合

image-20230726141729580

8.5.5 Single Joint Skin

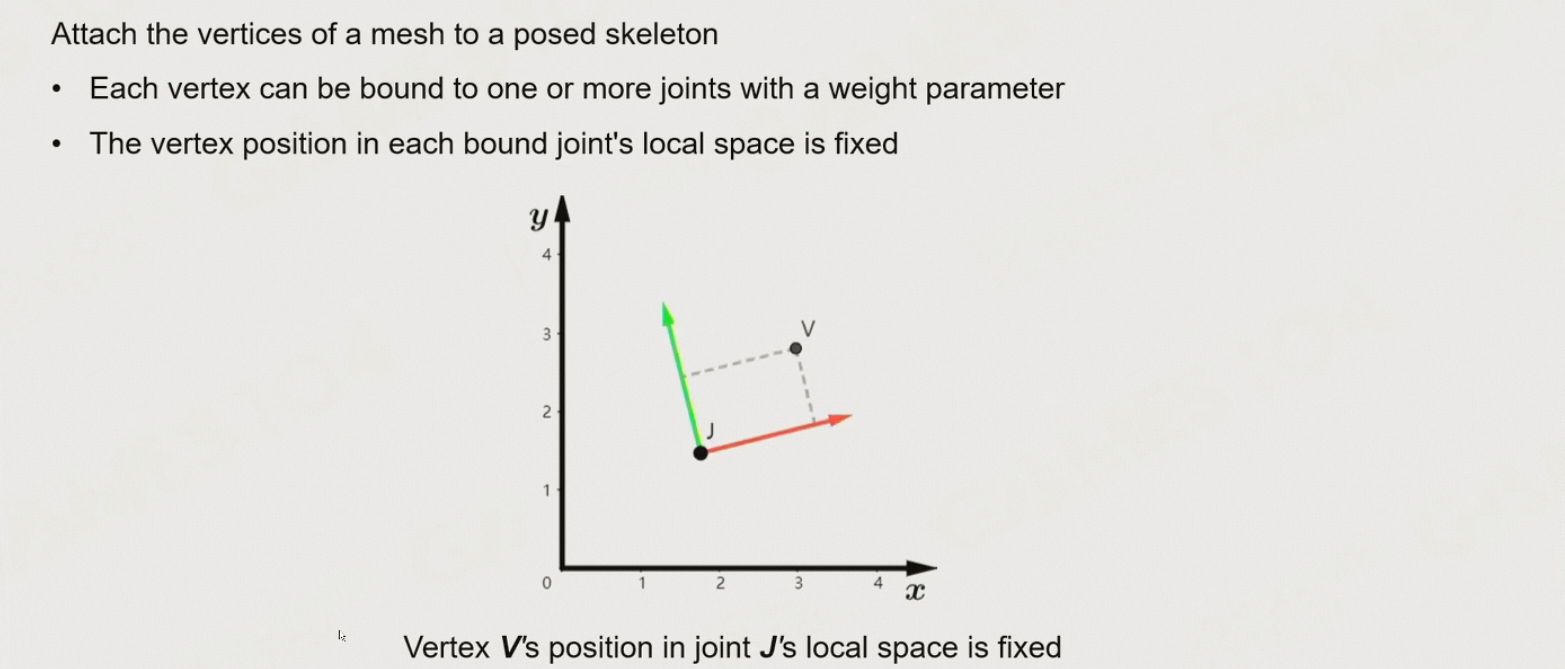
8.5.5.1 顶点相对于关节的局部坐标永远不变

将mesh上的一个顶点，绑定到一个骨骼上

  1. 每个顶点可以绑定一个或多个关节，每个关节有不同的权重
  2. 顶点在每个绑定关节的局部空间的位置是固定的

image-20230726142238716

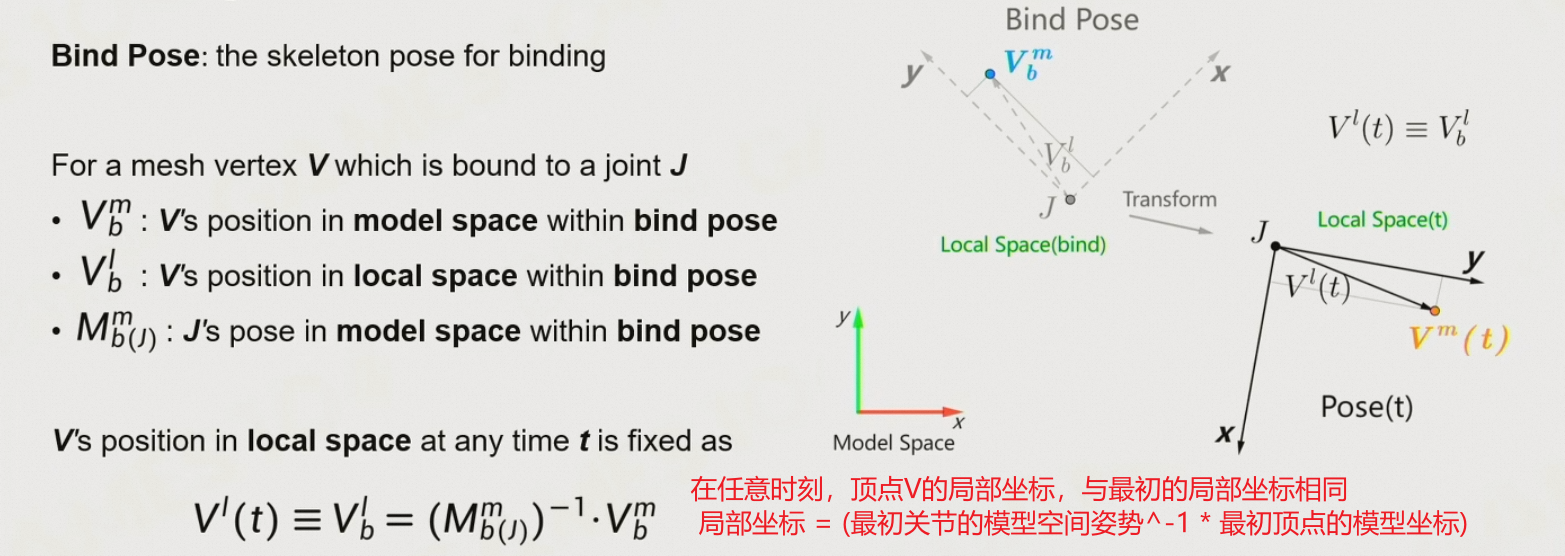
image-20230726143414912

image-20230726143513171

8.5.5.2 Skinning Matrix Palette

  1. 先计算每一个关节的Skinning Matrix，保存起来
  2. 在渲染顶点的时候，可以直接查表，不用重新计算蒙皮矩阵

优化：通常会再乘上\(M^w\)，将模型空间转化为世界空间

image-20230726143715728

8.5.5.3 在内存中表示一个骨骼

image-20230726144203453

8.5.6 Weighted Skinning with Multi-joints

  1. 每个mesh上的顶点会由多个关节同时作用
  2. 每个关节有不同的权重，但是要求权重和为1

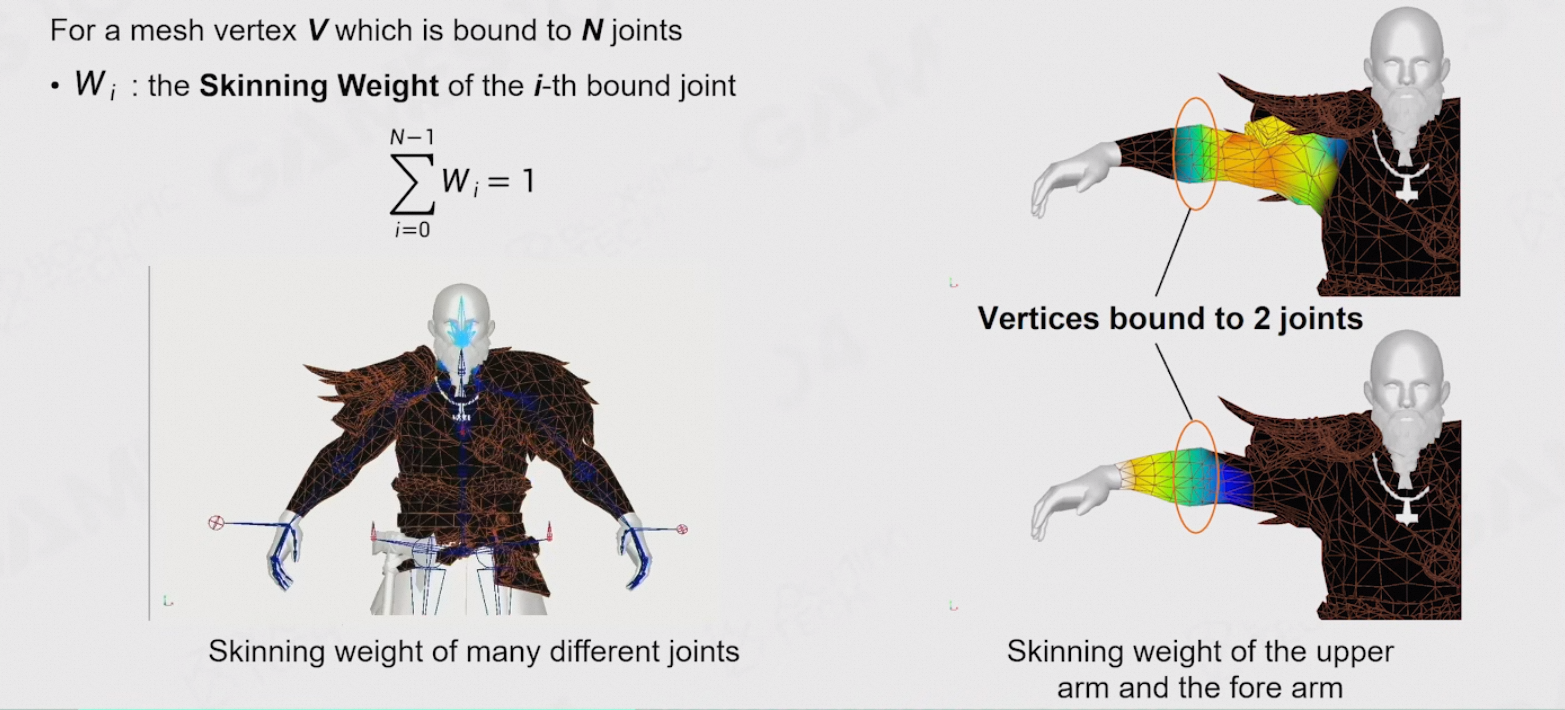
image-20230726144503596

  1. 计算每个关节对应的顶点的模型空间坐标，在模型空间中进行混合

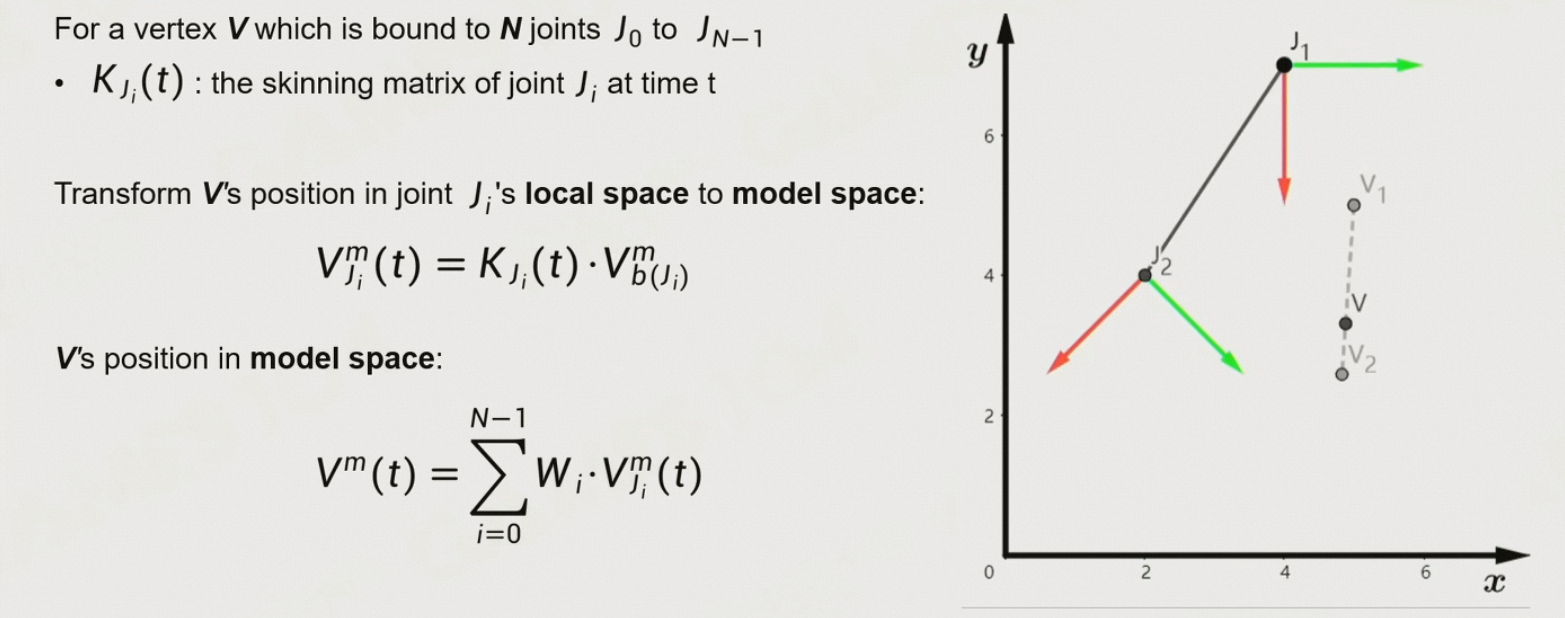
image-20230726144939033

8.5.7 Clip

将每一帧的骨骼姿势放在一个序列里面，称为一个clip

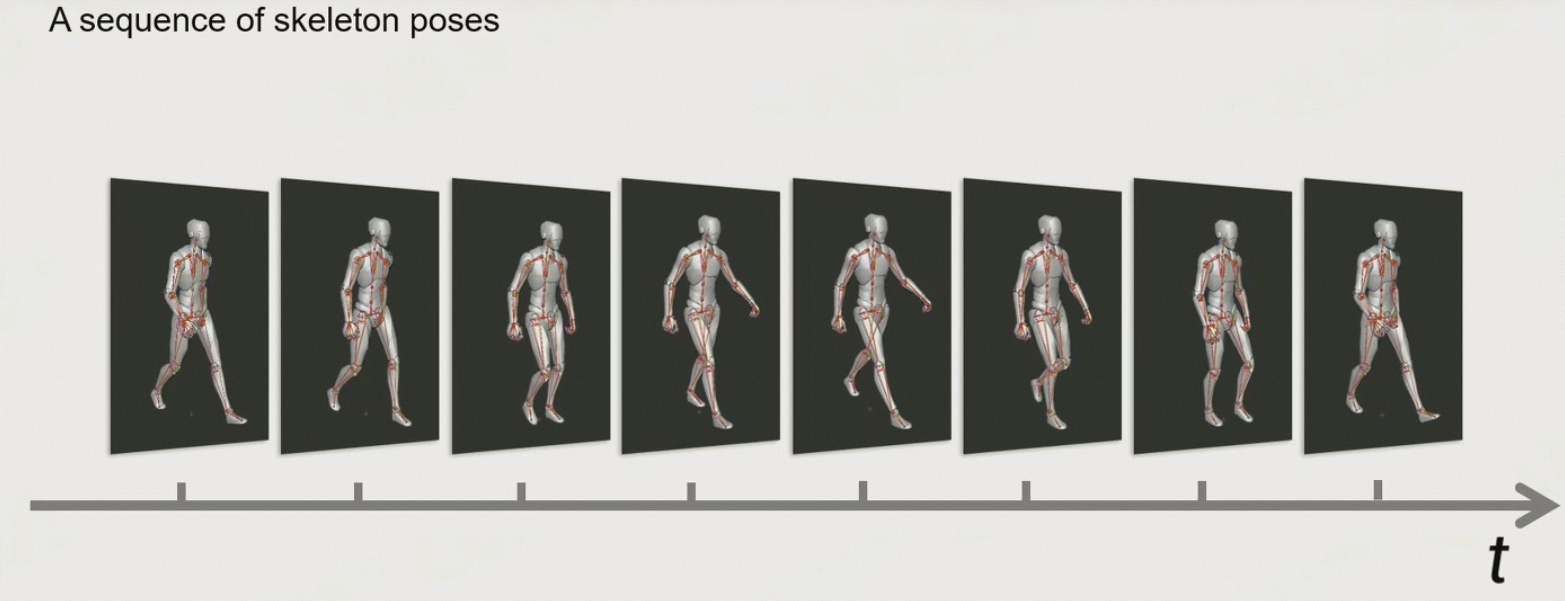
image-20230726145536660

8.5.8 在不同Pose之间进行插值

位移&缩放 lerp：线性插值

image-20230726145711201

旋转 Nlerp：q1和q2的线性插值，然后进行归一化

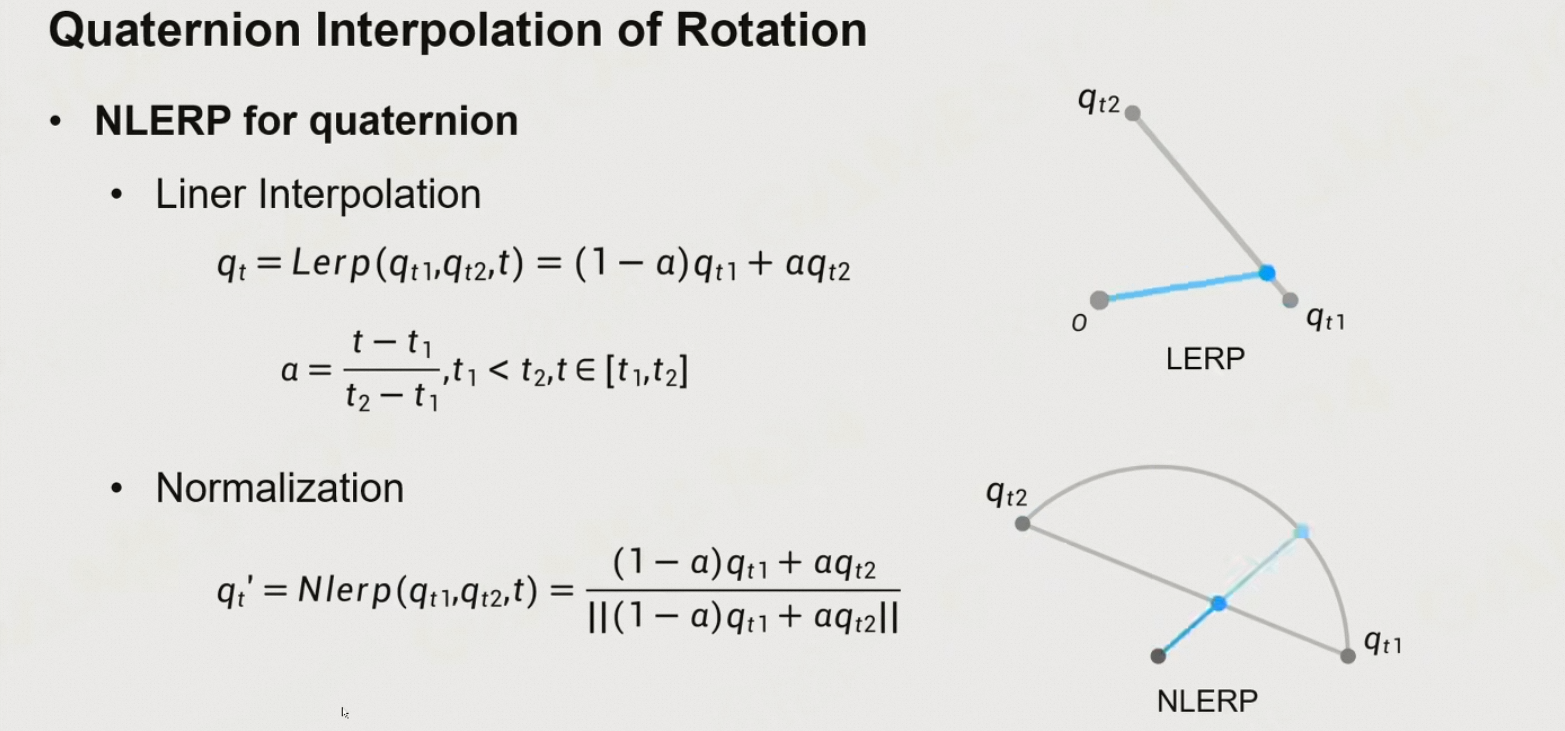
image-20230726145736080

最短路径插值：判断一下q1·q2，如果是<0，则需要反向插值

image-20230726150409999

Nlerp的问题：插值的角速度不恒定

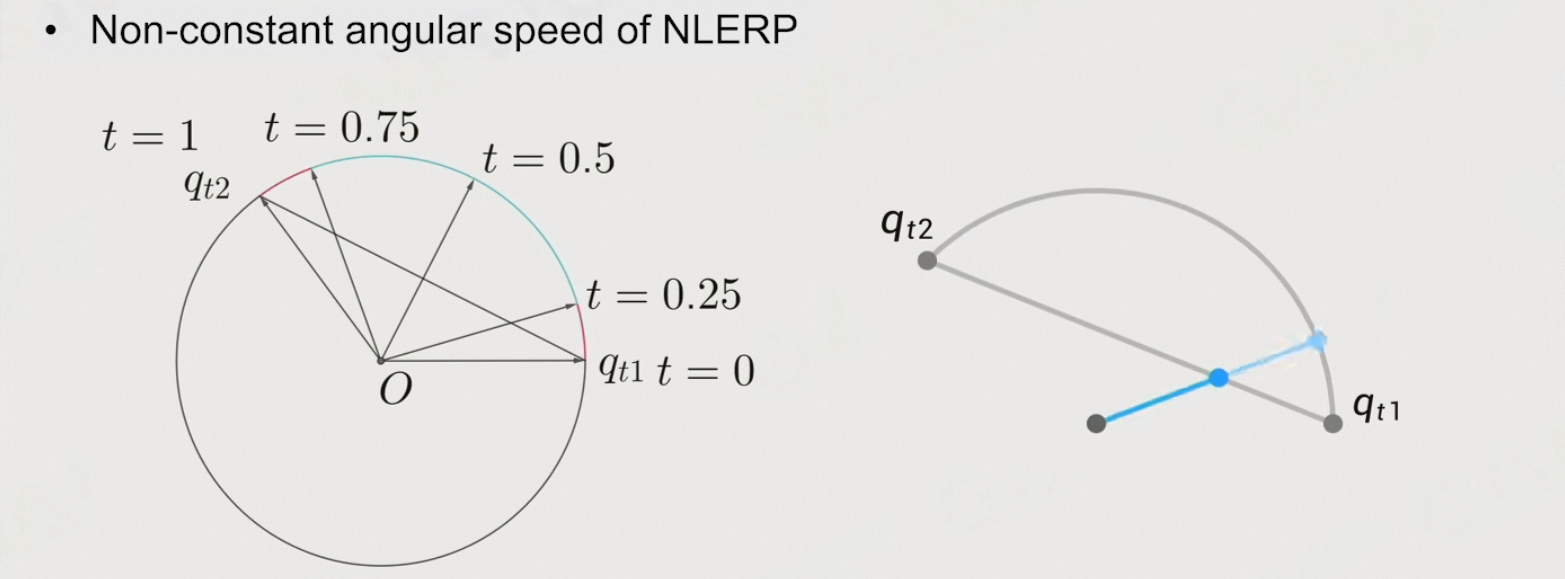
image-20230726150653720

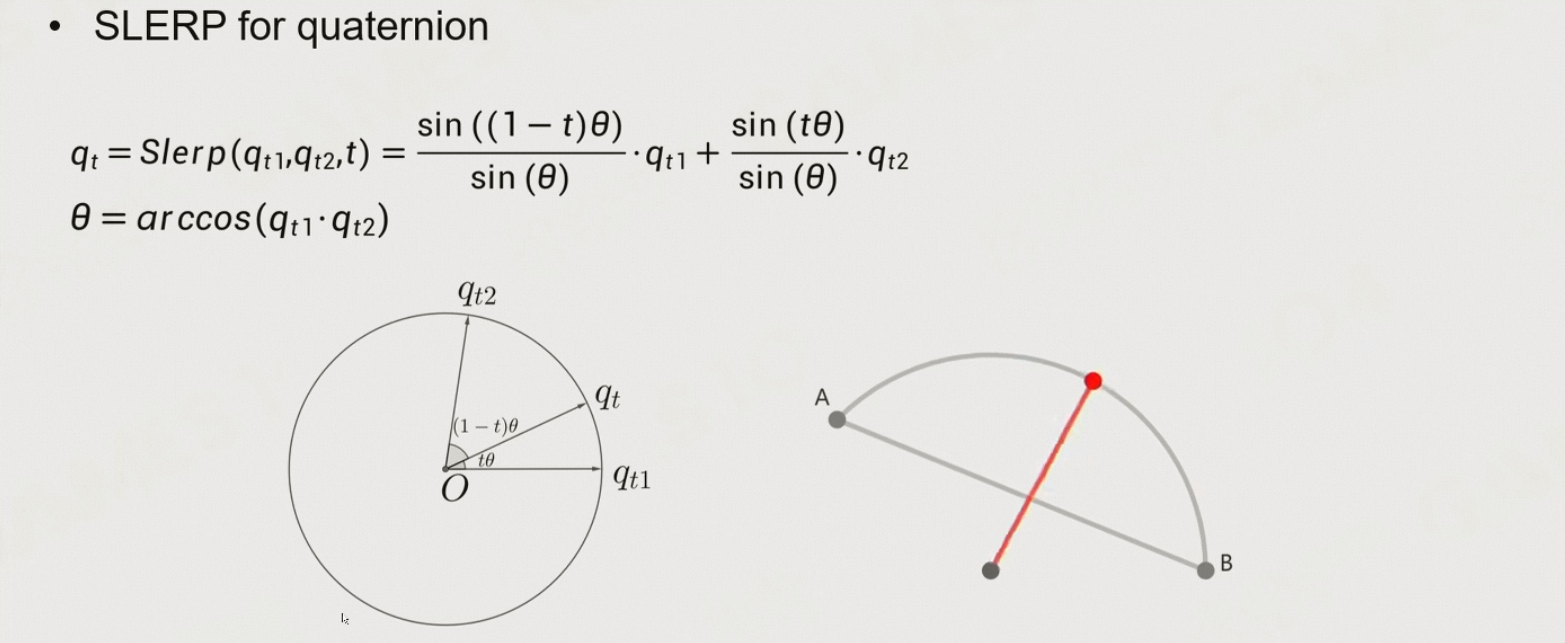
Slerp：通过arccos，计算两个方向的夹角，通过θ插值

  1. 但是计算比较费资源
  2. 并且当角度很小时，结果不精确
  3. 通常会指定一个角度，小于它用NLERP，大于它用SLERP

image-20230726150718402

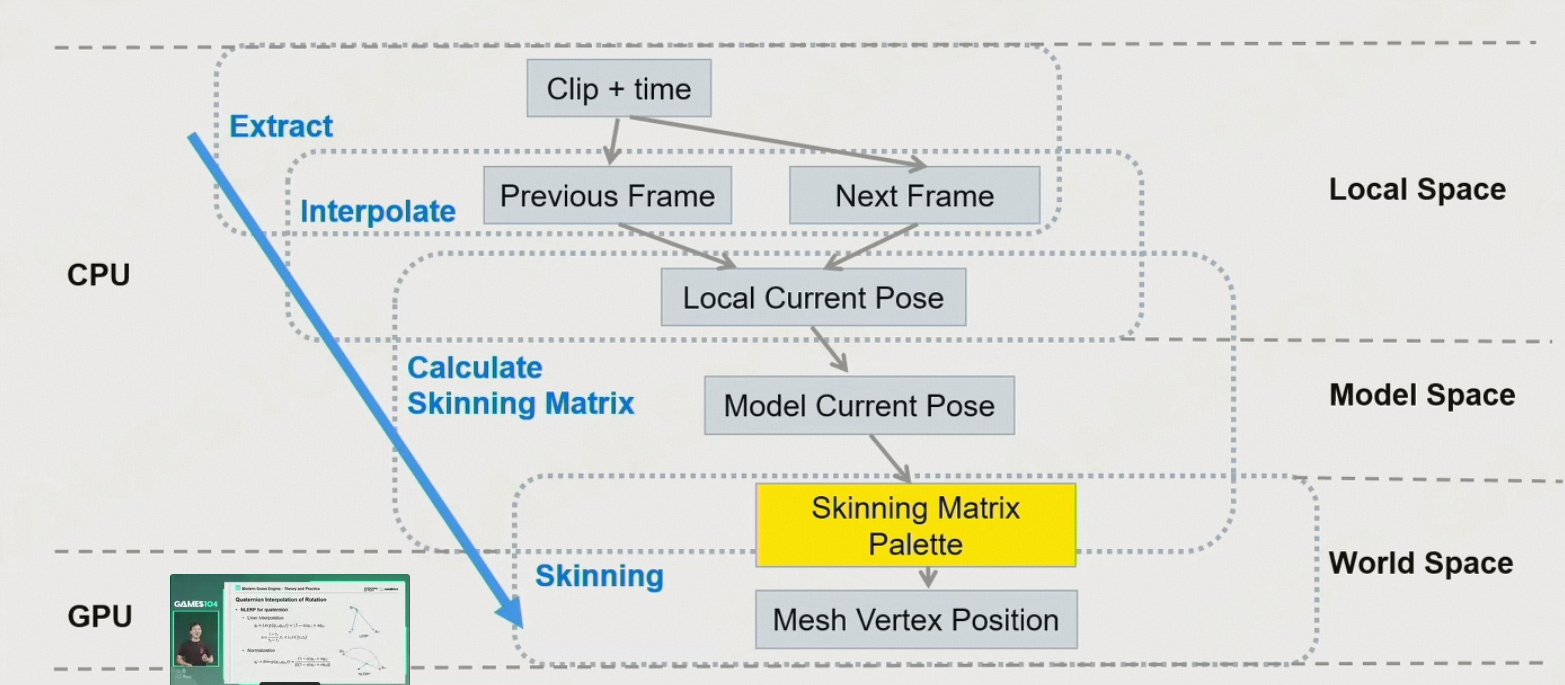
8.5.9 简单动画的Runtime Pipeline

image-20230726151230438

8.6 动画压缩技术

8.6.1 减少DoF

  1. Scale：直接忽略

  2. Translation：只存储最初的值

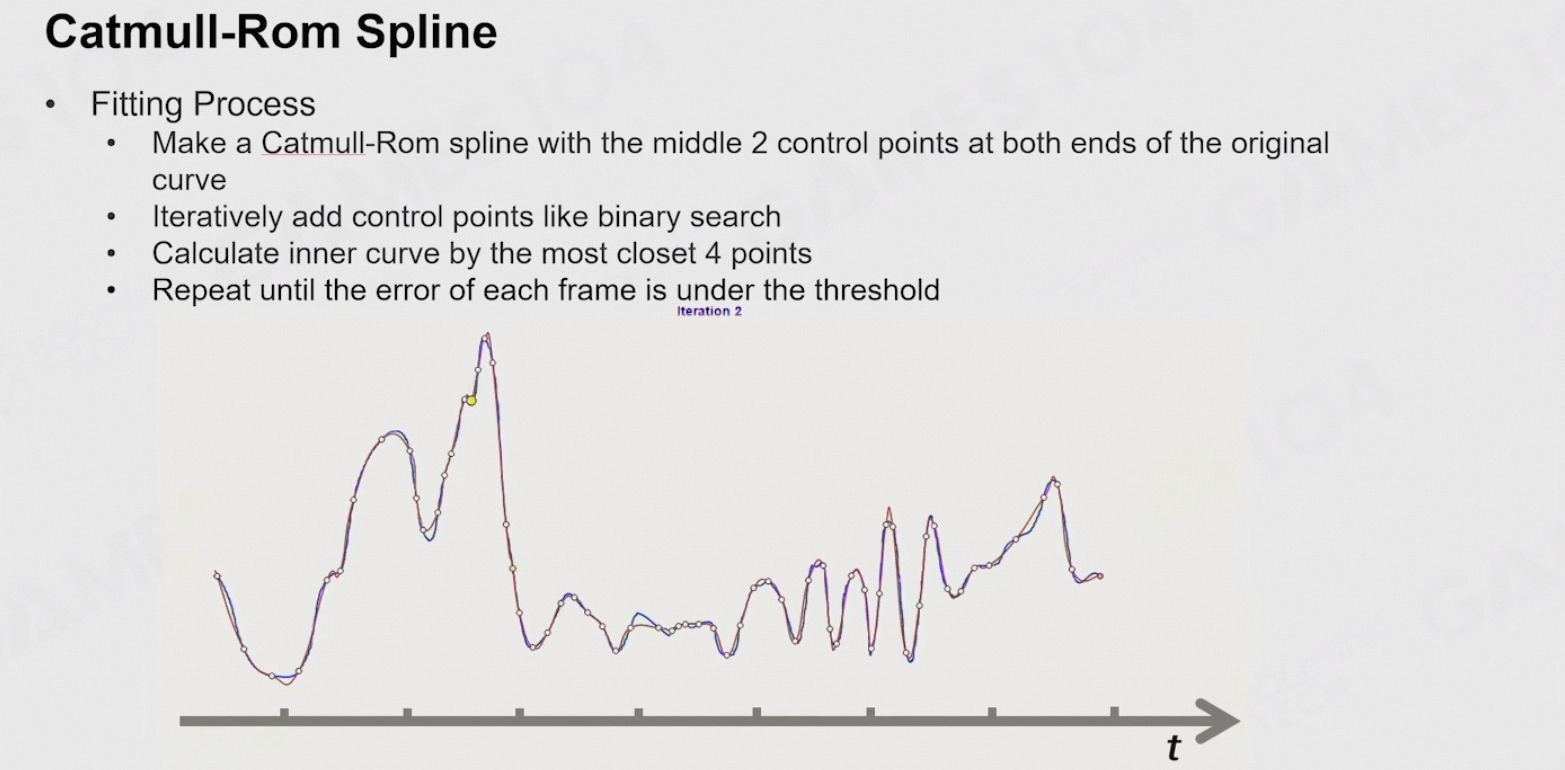
  3. Rotation：通过关键帧进行插值

    1. 以第0帧作为第一个关键帧，通过插值计算下一帧
    2. 如果误差高于某个值，则将其作为下一个关键帧

    image-20230726151745711

  4. Catmull-Rom曲线：

    1. 由四个控制点生成一个曲线，拟合原有的旋转曲线

    image-20230726151936487

    image-20230726152053696

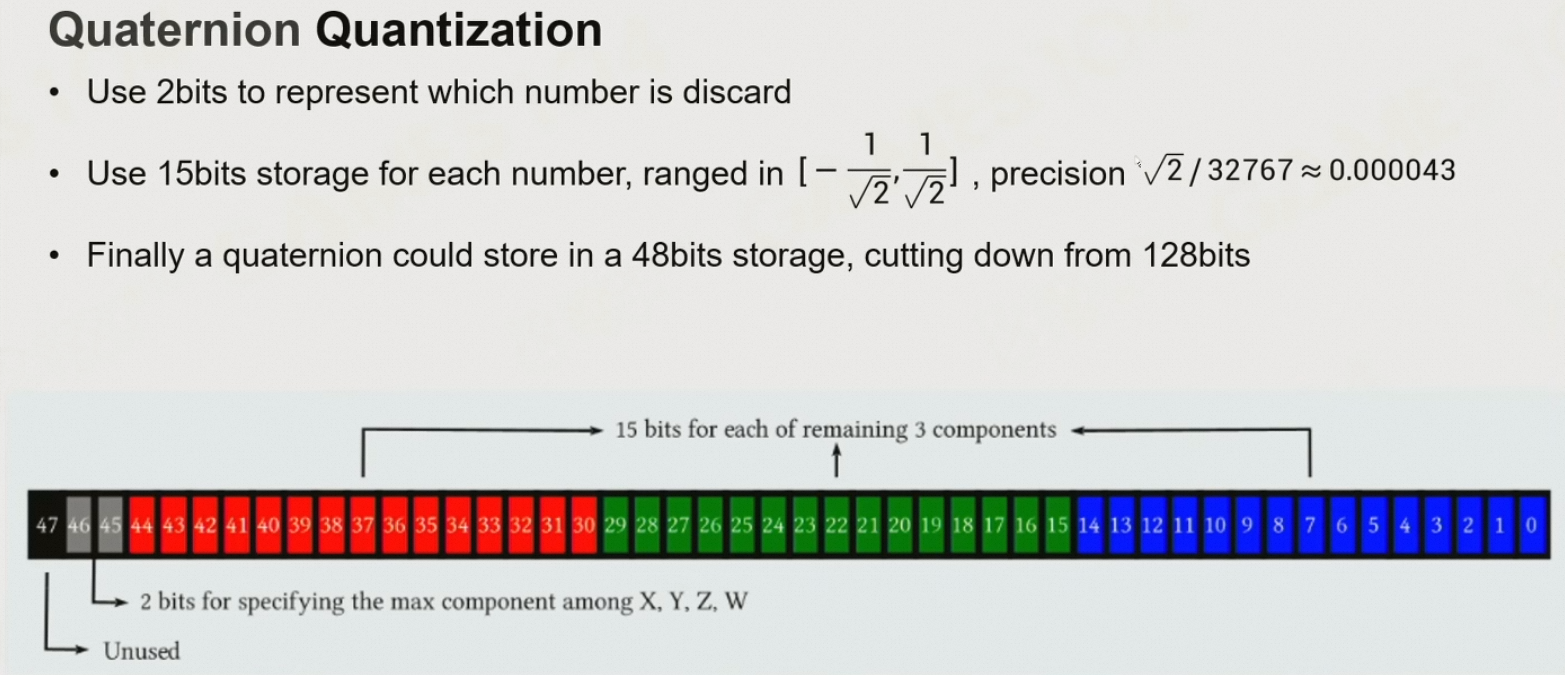
8.6.2 用定点数代替float

image-20230726152215646

image-20230726152341008

image-20230726152358663

8.6.3 误差传播

由于关节的模型坐标是从根节点累乘得到的，因此会导致误差的累积

image-20230726152529422

衡量精确度：Visual Error

image-20230726152700328

image-20230726152726472

误差补偿：子骨骼对父骨骼产生的误差进行补偿

  1. 缺点：父骨骼的误差叠加后，可能在子骨骼上产生高频数据，导致末端骨骼产生高频抖动

image-20230726153005119

8.7 动画制作流程

  1. 构建mesh，用低精度的mesh做动画

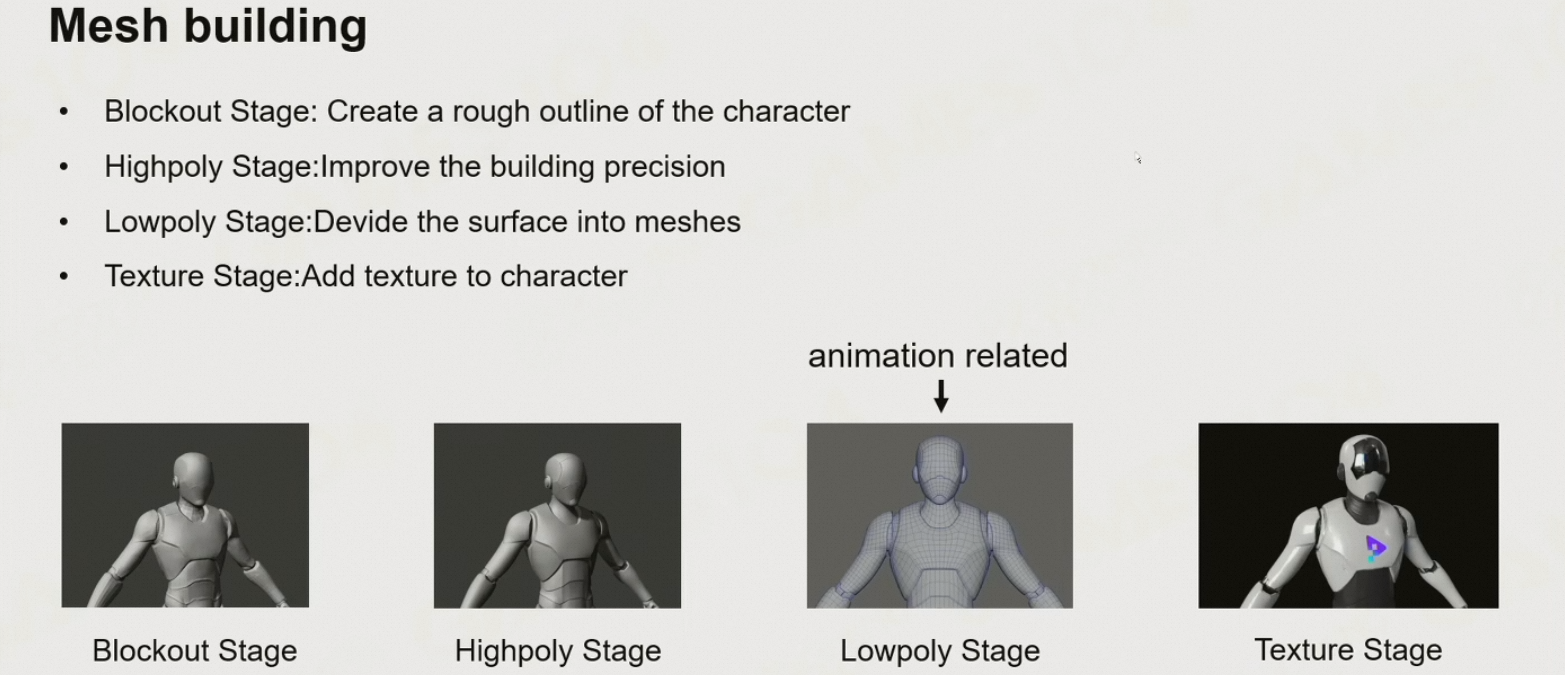
    image-20230726153201327

  2. 在关节处添加网格，防止关节处变形

    image-20230726153255760

  3. 骨架绑定，并添加Game Play关节（如武器关节、Pelvis、root）

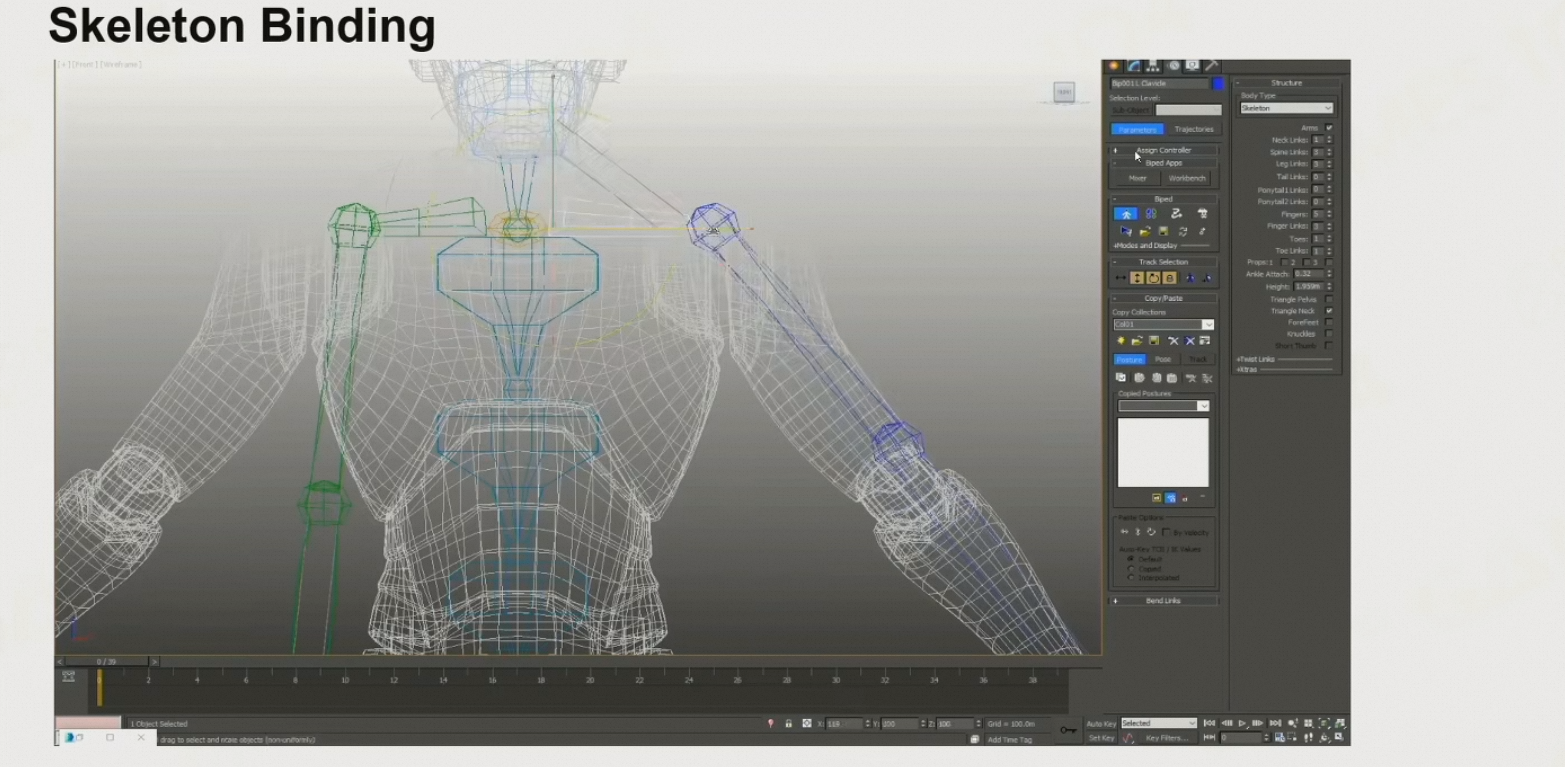
    image-20230726153358233

    image-20230726153421687

  4. 自动计算skinning

    image-20230726153522586

  5. 手动调整skinning

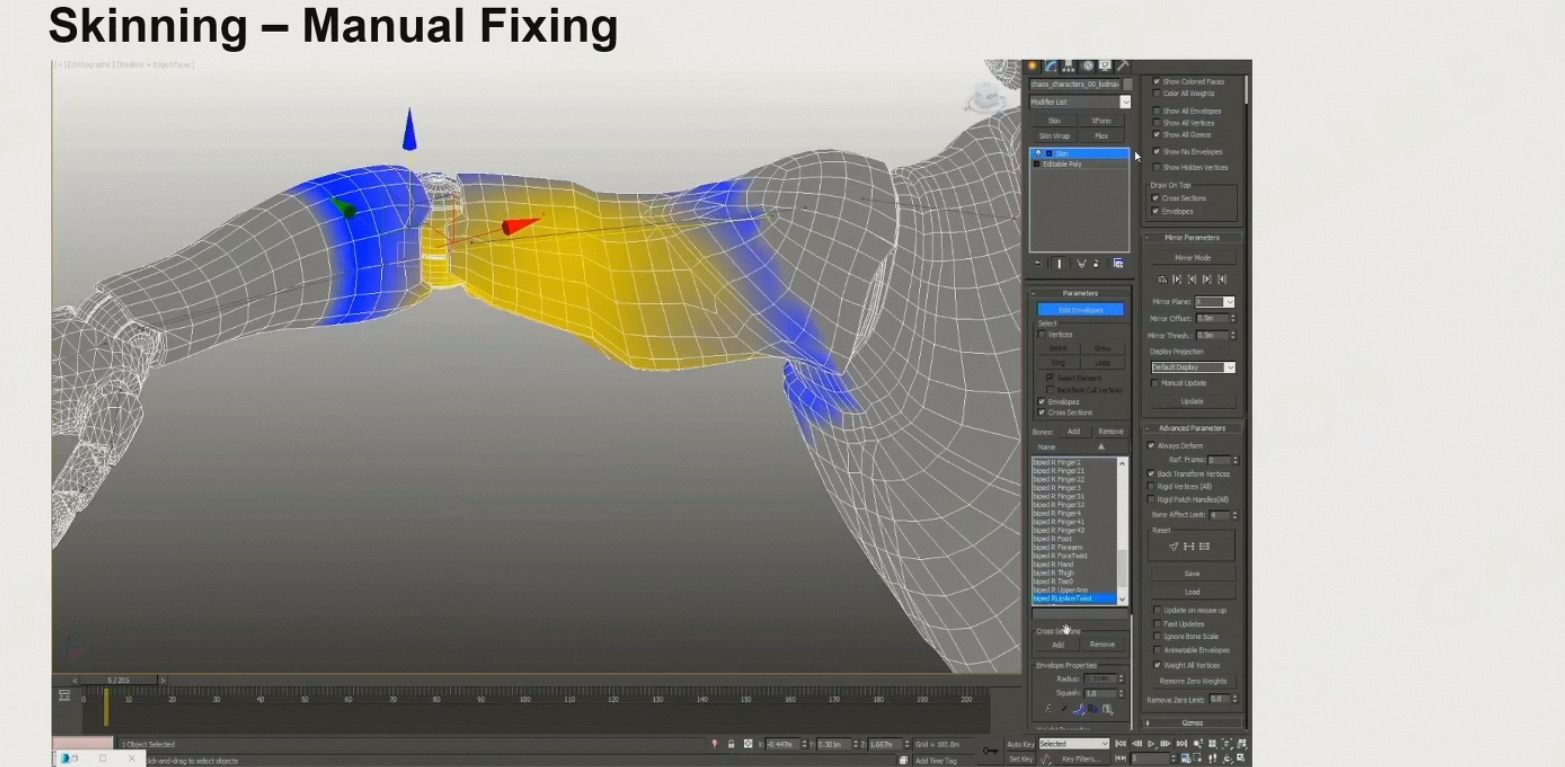
    image-20230726153553479

  6. 制作动画：设置关键帧及时间间隔

    image-20230726153629247

  7. 导出动画

    1. 如果在动画中root产生位移，会将root的移动单独导出为一个位移曲线给引擎用

    image-20230726153644960

    image-20230726153828377