Raytracing The Rest of Your Life

在线查看器

参考教程

项目代码

Chapter 1：A Simple Monte Carlo Program

蒙特卡罗方法（MC）是一种统计模拟方法，是一类很重要的数值计算方法，它是一种使用随机数解决好很多实际问题的方法

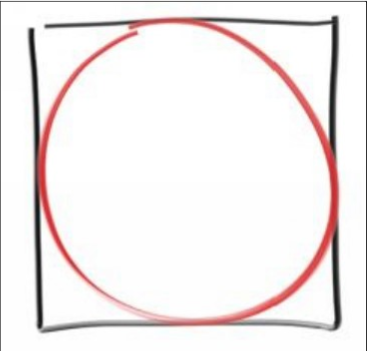
1.1 估计\(\pi\)

• 假设你扔了很多随机的点到方框中，那么有一部分在圆内，其中圆内点和方框点的比例应该就是圆的面积和方框面积的比例，由此： \[ 比例 = \frac{π * R * R}{(2R)*(2R)} = \frac{π}{4} \]

• 由于上式和R无关，我们任意取R = 1，圆心位于原点，则

#include <iostream>
#include "Math/Random.h"

void estimate_π(const size_t points) {
    int inside = 0;
    for (int i = 0; i < points; ++i) {
        double x = 2 * Random::rand01() - 1;
        double y = 2 * Random::rand01() - 1;
        if (x*x + y*y < 1) inside++;
    }
    std::cout << "Estimate of π by" << points << "test points is " << 4 * double(inside) / points << std::endl;
}

int main(){	　　
    estimate_π(1000);	　　
    estimate_π(10000);	　　
    estimate_π(100000);	　　
    estimate_π(1000000);	　　
    estimate_π(10000000);	　　
    estimate_π(10000000/2);
    return 0;
}

1.2 分层方法

• 一开始非常快速的逼近\(π\)，之后变化就比较缓慢了，这是一个收益递减法(Law of Diminishing Returns)的例子
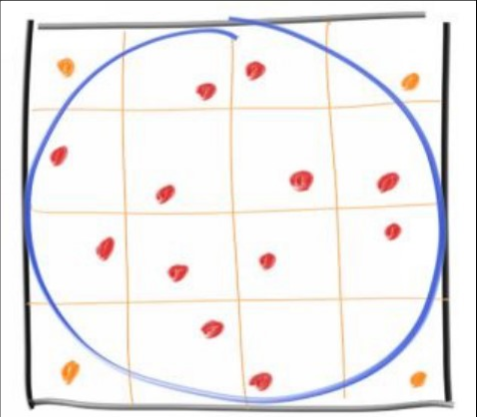
• 即每一个样本对结果的收益少于后面一个，这个是MC的一个缺点，我们可以通过对样本进行分层来减轻这种递减收益，此法通常称为抖动
• 我们进行网格划分，并在每个网格中选取一个样本：

我们采用边长为1e4的方框进行测试

void stratify() {
    size_t inside{ 0 };
    size_t circle_stratified{ 0 };
    size_t sqrtAll = 1e4;
    for (int i = 0; i < sqrtAll; ++i)
        for (int j = 0; j < sqrtAll; ++j) {
            double x = 2 * Random::rand01() - 1;
            double y = 2 * Random::rand01() - 1;
            if (x*x + y*y < 1) inside++;
            
            x = 2 * ((i + Random::rand01()) / sqrtAll) - 1;
            y = 2 * ((j + Random::rand01()) / sqrtAll) - 1;
            if (x*x + y*y < 1) circle_stratified++;
        }
    std::cout << "Regular Estimate of π by 1e8 test points is " << 4 * double(inside) / 1e8 << stds endl;
    std::cout << "Stratified Estimate of π by 1e8 test points is " << 4 * double(circle_stratified) / 1e8 << stds endl;
}

• 分层方法能更好地收敛于渐近率。不足之处是，这个优势随着问题的维度而降低（例如，对于3D球体积版本，差距会更小）。 这被称为维度诅咒（=.=）
• 我们的工程将是非常高的维度（每个反射增加两个维度），所以我不会在本书中进行分层。
• 但是，如果你做的是单反射或阴影或某些严格的2D问题，分层是个很好的选择

Chapter 2：One Dimensional MC Integration

2.1 相关概念

• PDF：\(p(x)\)，表示随机变量取值为\(x\)的概率，值域为\((0,∞)\)
• CPDF：\(P(x)=\int_{-∞}^x p(x)\)，表示从负无穷到x的累积概率，值域为\((0,1)\)

当我们使用rand01()获得满足\((0,1)\)之间平均分布的变量\(Y\)时，其对应的是\(P(x)\)

• 因此我们需要使用CPDF的反函数\(P^{-1}(Y)\)，获得满足我们需要的随机变量\(x\)
• \(x\)满足\(p(x)\)定义的分布

• 假设我们希望随机变量\(x\)满足\(p(x)=\frac{x}{2}\)
• 首先求出CPDF：\(P(x)=\frac{x^2}{4}\)
• 然后求反函数：\(P^{-1}(Y)=\sqrt{4Y}\)
• 从而得到生成随机变量\(x\)的代码为：x = sqrt(4 * rand01())

2.2 重要性采样 & 蒙特卡洛积分

\[ S = \frac{1}{n} * \sum\frac{F(x_i)}{p(x_i)} \]

• PDF的最优函数：被积函数本身

2.3 示例：\(\int \cos^2 θ\ dθ\)

• PDF：均匀采样
• \(S = \frac{1}{n} * \sum\frac{\cos^2 θ}{p(direction)} = \frac{1}{n} * \sum\frac{\cos^2 θ}{1/4\pi}\)

void sphereMC() {
    auto pdf = []() { return 1 / (4 * π); };
    size_t n = 10000000;
    double sum = 0;
    for (int i = 0; i < n; i++) {
        dvec3 d = Random::random_unit_sphere();
        double cosine = d.z()*d.z();
        sum += cosine / pdf();
    }
    std::cout << "I = " << sum / n << stds endl;
}

Chapter 3：Light Scaterring

• \(albedo\)：光线被反射的概率

3.1 光的散射

对于光的散射而言，可以基于立体角，设计一个PDF来描述光线散射的方向分布

• 记为：\(s(direction)\)
• 这个散射PDF会随着入射方向的变化而变化

对于表面色彩而言，有如下积分形式： \[ color=\int albedo * s(direciont) * color(direction)\ dθ \]

• 其中，\(albedo\)、\(s(direction)\)都是依赖于观察方向的，因此\(color\)也会随着观察方向的变化而变化
• \(albedo\)、\(s(direction)\)也可能随着表面或物体的位置而变化

使用蒙特卡洛方法计算该积分： \[ color=\frac{1}{n} * \sum \frac{albedo * s(direciont) * color(direction)}{pdf(direction)} \]

3.2 Lambertian材质的表面散射PDF

• Lambertian材质的表面密度，呈余弦规律
• 因此，Lambertian表面的光散射PDF是正比于\(\cos θ\)
  • \(θ\)：光线方向和表面法线的夹角
• 此外，我们定义：\(\cos θ < 0\)时，\(s(direction)=0\)
  • 因此有效区间为半球面

半球面积的计算如下： \[ \begin{aligned} S &= \iint_{A} \cosθ dA \\ &= \int_{0}^{2\pi} \int_0^{\frac{\pi}{2}} \cosθ \sinθ \ dθdΦ\\ &= \int_{0}^{2\pi} dΦ \int_0^{\frac{\pi}{2}} \cosθ \sinθ \ dθ\\ &= \int_{0}^{2\pi} dΦ \int_0^{\frac{\pi}{2}} \frac{1}{2} \sin2θ dθ\\ &= \pi \end{aligned} \] 因此，Lambertian材质的表面散射PDF为： \[ s(direction) = \frac{\cosθ}{\pi} \]

• 为了保证采样的最优性，我们也使用同样的PDF函数：\(p(direction) = \frac{\cosθ}{\pi}\)
• 此时\(s\)和\(p\)可以约去，得到\(color=albedo * color(direction)\)，这也是我们原始的color函数中的设定

使用BRDF描述表面散射为： \[ BRDF=\frac{albedo*s(direction)}{\cosθ} \]

• 对于Lambertian材质，\(BRDF=\frac{albedo}{\pi}\)

Chapter 4：Important Sampling Materials

4.1 相关概念

• 目标：向光源发送额外的光线，降低图片的噪声

• 设：

  • \(pLight(direction)\)：发射的一束朝向光源的光线的PDF
  • \(pSurface(diection)\)：与s有关的PDF

• 将两者线性组合，得到一个综合的PDF： \[ p(direction)=0.5*pLight(direction) + 0.5*pSurface(direction) \]

  • 注意：要求权重是正的，并且和为1

• 设计PDF最重要的一点是，让其尽可能接近于\(s(direction)*color(direction)\)的分布

  • 对于漫反射表面，我们猜测它更偏重\(color(direction)\)因子
  • 对于镜面材质表面，\(s(direction)\)只在一个方向附近很大，因此它更重要

4.2 对material基类的修改

class Material {
public:
	/*
	* @brief 生成散射光线
	* @param r_in 入射光线
	* @param info 碰撞信息
	* @param attenuation 当发生散射时, 光强如何衰减, 分为rgb三个分量
	* @param r_out 散射光线
	* @return 是否得到了散射光线
	*/
	virtual bool scatter(const Ray& r_in, const HitInfo& info, Color& attenuation, Ray& r_out) const = 0;

	/*
	* @brief 生成散射光线
	* @param r_in 入射光线
	* @param info 碰撞信息
	* @param attenuation 当发生散射时, 光强如何衰减, 分为rgb三个分量
	* @param r_out 散射光线
	* @param pdf 重要性采样的pdf取值
	* @return 是否得到了散射光线
	*/
	virtual bool scatter(const Ray& r_in, const HitInfo& info, Color& attenuation, Ray& r_out, double& pdf) const {
		return scatter(r_in, info, attenuation, r_out);
	}


	/*
	* @brief 计算散射pdf的取值
	* @param r_in 入射光线
	* @param info 碰撞信息
	* @param r_out 散射光线
	* @return pdf取值
	*/
	virtual double scatter_pdf(const Ray& r_in, const HitInfo& info, const Ray& r_out) const {
		return 1;
	}

	/*
	* @brief 自发光
	* @param u uv坐标
	* @param v uv坐标
	* @param p 碰撞点
	*/
	virtual Color emitted(double u, double v, const Point3& p) const {
		return Color(0, 0, 0);
	}
};

4.3 对Lambertian的修改

bool Lambertian::scatter(const Ray& r_in, const HitInfo& info, Color& attenuation, Ray& r_out) const {
	// 漫反射: 在单位圆内随机取一点, 作为反射方向
	Vec3 target = info.position + info.normal + Random::rand_unit_sphere();
	r_out = Ray(info.position, target - info.position, r_in.Time());
	attenuation = albedo->Value(info.u, info.v, info.position);
	return true;
}

bool Lambertian::scatter(const Ray& r_in, const HitInfo& info, Color& attenuation, Ray& r_out, double& pdf) const {
	// 漫反射: 在单位圆内随机取一点, 作为反射方向
	Vec3 target = info.position + info.normal + Random::rand_unit_sphere();
	r_out = Ray(info.position, target - info.position, r_in.Time());
	attenuation = albedo->Value(info.u, info.v, info.position);
	pdf = info.normal.dot(r_out.Direction()) / PI;
	return true;
}

double Lambertian::scatter_pdf(const Ray& r_in, const HitInfo& info, const Ray& r_out) const {
	double cosine = info.normal.dot(r_out.Direction());
	if (cosine < 0) cosine = 0;
	return cosine / PI;
}

Chapter 5：Generating Random Direction

5.1 三维随机方向向量的生成

假定：

• Z轴：表面法线
• θ：与法线的夹角
• 仅处理关于z轴旋转对称的分布，其他相关的量，均设为均匀分布

5.2 \(pdf(direction)=f(θ)\)

\[ \begin{aligned} g(Φ)&=\frac{1}{2\pi}\\ h(θ)&=2\pi f(θ) \sin θ \end{aligned} \]

对于满足\([0,1]\)之间均匀分布的随机变量\(r_1,r_2\)而言： \[ \begin{aligned} r_1 &= \int_{0}^{Φ} \frac{1}{2\pi} dθ = \frac{Φ}{2\pi} \\ r_2 &= \int_{0}^{θ} 2\pi f(t) \sin t \ dt \end{aligned} \]

5.2.1 \(pdf(direction)=f(θ)=\frac{1}{4\pi}\)

\[ \begin{aligned} r_1 &= \int_{0}^{Φ} \frac{1}{2\pi} dθ = \frac{Φ}{2\pi} \\ r_2 &= \int_{0}^{θ} 2\pi \frac{1}{4\pi} \sin t \ dt\\ &= \int_{0}^{θ} \frac{1}{2} \sin t \ dt\\ &= \frac{1-\cos θ}{2} \end{aligned} \]

从而： \[ \begin{aligned} Φ &= 2\pi r_1 \\ \cos θ &= 1 - 2r_2 \end{aligned} \] 带入球坐标得： $$ \[\begin{aligned} x &= \cosΦ\sinθ = 2\cos(2\pi r_1) * \sqrt{r_2(1-r_2)} \\ y &= \sinΦ\sinθ = 2\sin(2\pi r_1) * \sqrt{r_2(1-r_2)}& \\ z &= \cosθ = 1-2r_2 \end{aligned}\]

$$

5.2.2 \(pdf(direction)=f(θ)=\frac{1}{2\pi}\)

\[ \begin{aligned} r_1 &= \int_{0}^{Φ} \frac{1}{2\pi} dθ = \frac{Φ}{2\pi} \\ r_2 &= \int_{0}^{θ} 2\pi \frac{1}{2\pi} \sin t \ dt\\ &= \int_{0}^{θ} \sin t \ dt\\ &= 1-\cos θ \end{aligned} \]

从而： \[ \begin{aligned} Φ &= 2\pi r_1 \\ \cos θ &= 1 - r_2 \end{aligned} \] 带入球坐标得： $$ \[\begin{aligned} x &= \cosΦ\sinθ = \cos(2\pi r_1) * \sqrt{r_2(2-r_2)} \\ y &= \sinΦ\sinθ = \sin(2\pi r_1) * \sqrt{r_2(2-r_2)}& \\ z &= \cosθ = 1-r_2 \end{aligned}\]

$$

5.2.3 \(pdf(direction)=f(θ)=\frac{\cos θ}{4\pi}\)

\[ \begin{aligned} r_1 &= \int_{0}^{Φ} \frac{1}{2\pi} dθ = \frac{Φ}{2\pi} \\ r_2 &= \int_{0}^{θ} 2\pi \frac{\cos t}{4\pi} \sin t \ dt\\ &= \int_{0}^{θ} \frac{1}{2} \sin t \cos t \ dt\\ &= 1-\cos^2 θ \end{aligned} \]

从而： \[ \begin{aligned} Φ &= 2\pi r_1 \\ \cos θ &= \sqrt{1 - r_2} \end{aligned} \] 带入球坐标得： $$ \[\begin{aligned} x &= \cosΦ\sinθ = 2\cos(2\pi r_1) * \sqrt{r_2} \\ y &= \sinΦ\sinθ = 2\sin(2\pi r_1) * \sqrt{r_2}& \\ z &= \cosθ = \sqrt{1 - r_2} \end{aligned}\]

$$

static Vec3 rand_cosine_direction() {
	double r1 = rand01();
	double r2 = rand01();

	double x = cos(2 * PI * r1) * sqrt(r2);
	double y = sin(2 * PI * r1) * sqrt(r2);
	double z = sqrt(1 - r2);
	return Vec3(x, y, z);
}

Chapter 6：Ortho-normal Bases

目标：将Chapter 5中基于z轴的随机方向，转化为基于表面法线的随机方向

6.1 建立基于表面法线的坐标系

• \(\bold{n}\)：表面法线
• \(\bold{t}\)：\(\bold{t}=cross(\bold{vup},\bold{n})\)
• \(\bold{s}\)：\(\bold{s}=cross(\bold{t},\bold{n})\)
• 坐标系中的任意一点\((x,y,z)\)表示如下：
  • 随机向量 = \(x\bold{s}+y\bold{t}+z\bold{n}\)

class ONB {
public:
	/*
	* @brief 根据法线构建局部坐标系
	* @param normal 法线
	*/
	ONB(Vec3 normal);

	/*
	* @brief 获取局部坐标对应的世界坐标
	*/
	Vec3 local(double x, double y, double z) const;

	/*
	* @brief 获取局部坐标对应的世界坐标
	*/
	Vec3 local(const Vec3& v) const;

private:
	/*
	* @brief 根据法线构建局部坐标系
	* @param normal 法线
	*/
	void build_from_w(const Vec3& normal);


public:
	const Vec3& operator[](int index) const { return axis[index]; }
	const Vec3& u() const { return axis[0]; }
	const Vec3& v() const { return axis[1]; }
	const Vec3& w() const { return axis[2]; }

private:
	Vec3 axis[3];
};

ONB::ONB(Vec3 normal) {
    build_from_w(normal);
}

Vec3 ONB::local(double x, double y, double z) const {
    return x * u() + y * v() + z * w();
}

Vec3 ONB::local(const Vec3& v) const {
    return local(v[0], v[1], v[2]);
}

void ONB::build_from_w(const Vec3& normal) {
    Vec3 n = normal.normalize();

    Vec3 vup(1, 0, 0);
    if (fabs(n.x()) > 0.9) vup = Vec3(0, 1, 0);

    axis[2] = n;
    axis[1] = n.cross(vup).normalize();
    axis[0] = n.cross(axis[1]).normalize();
}

6.2 修改 Lambertian 材质的scatter函数

bool Lambertian::scatter(const Ray& r_in, const HitInfo& info, Color& attenuation, Ray& r_out, double& pdf) const {
	ONB uvw(info.normal);
	do {
		// 在单位球上随机采样方向, 作为出射方向, 然后将其转化为全局坐标
		Vec3 direction = uvw.local(Random::rand_cosine_direction());
		
		// 构建出射光线
		r_out = Ray(info.position, direction.normalize(), r_in.Time());
		
		// 重要性采样 pdf = cosθ / π
		pdf = uvw.w().dot(r_out.Direction()) / PI;
	} while (pdf == 0);

	attenuation = albedo->Value(info.u, info.v, info.position);
	return true;
}

Chapter 7：Sample Lights Directly

• 即直接朝光源方向发射光线
• 重点在于计算\(pdf(direction)\)

7.1 直接光源采样

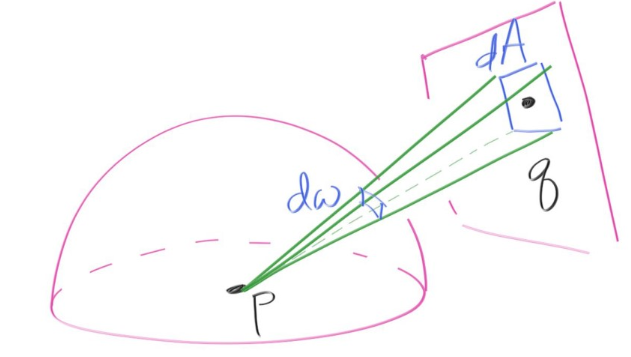
• 对于一个光源区域A，如果均匀采样该区域，则\(p\_q(q)=\frac{dA}{A}\)

• 但是由于积分区域是物体表面的单位球，因此我们需要将\(pdf\)进行转换，即将光源处的微分\(dA\)转化为方位角微分\(dΩ\) \[ dΩ=\frac{\cos α}{distance^2}dA \]

• 由于\(dA\)和\(dΩ\)对应的区域的概率是相同的，因此有如下等式： \[ p(direction) * dΩ = p\_q(q) * dA \\ \]

• 因此有 \[ p(direction) = \frac{distance^2}{\cos α *A} \]

7.2 修改GetColor的采样

Color ObjectWorld::GetColor(const Ray& r, int& depth) {
	HitInfo info;

	// 如果碰撞到了, 则根据材质计算反射光线
	// 注意 t_min 需要设置一个很小的值, 否则会出现光线重复与同一个物体相交的情况
	if (this->hit(r, 0.01, INFINITY, info)) {
		Ray r_out;
		Color emit = info.material->emitted(r, info, info.u, info.v, info.position);
		Color attenuation;
		double pdf;

		if (depth < max_depth && info.material->scatter(r, info, attenuation, r_out, pdf)) {
			// 直接光源采样: 在光源上随机采样一个点
			Point3 on_light = Vec3(213 + Random::rand01() * (343 - 213), 554, 227 + Random::rand01() * (332 - 227));
			// 计算方向及距离
			Vec3 direction = on_light - info.position;
			double distance_squared = direction.length_squared();
			direction = direction.normalize();
			if(direction.dot(info.normal) < 0) return emit;

			// 计算 pdf
			double A = (343 - 213) * (332 - 227);
			double cos_alpha = fabs(direction.y());
			if (cos_alpha < 1e-6) return emit;

			// pdf = distance^2 / (cos_alpha * A)
			pdf = distance_squared / (cos_alpha * A);

			// 向光源方向发射光线
			r_out = Ray(info.position, direction, r.Time());

			return emit + attenuation * info.material->scatter_pdf(r, info, r_out) * GetColor(r_out, ++depth) / pdf;
		}
		else
			return emit;
	}
	// 如果不相交, 则返回黑色
	else {
		return Color(0);
	}	
}

Chapter 8：混合概率密度

设计pdf的一个很重要的原则：使得累积概率密度达到且只达到1

8.1 pdf基类

主要的任务

• 获取\(pdf(direction)\)
• 按照当前模型，生成\(direction\)

class PDF {
public:
	/*
	* @brief 获取 direction 对应的概率密度
	* @param direction 随机方向
	* @return 概率密度
	*/
	virtual double value(const Vec3& direction) const = 0;

	/*
	* @brief 生成随机方向
	*/
	virtual Vec3 generate() const = 0;
};

8.1.1 \(pdf(direction)=f(θ)=\frac{\cos θ}{4\pi}\)

class PDF_cos : public PDF {
public:
	/*
	* @brief 随机方向满足 cos 分布
	* @param normal 法线
	*/
	PDF_cos(const Vec3& normal) : uvw(normal) {}

	/*
	* @brief 获取 direction 对应的概率密度
	* @param direction 随机方向
	* @return 概率密度
	*/
	virtual double value(const Vec3& direction) const override;

	/*
	* @brief 生成随机方向
	*/
	virtual Vec3 generate() const override;

private:
	ONB uvw;
};

double PDF_cos::value(const Vec3& direction) const {
	double cosine = direction.normalize().dot(uvw.w());
	if(cosine > 0) return cosine / PI;
	else return 0;
}

Vec3 PDF_cos::generate() const {
	return uvw.local(Random::rand_cosine_direction());
}

8.1.2 直接光源采样

class PDF_hit : public PDF {
public:
	/*
	* @brief 直接光源采样
	* @param light 光源
	* @param origin 观察点
	*/
	PDF_hit(Ref<Object> light, Point3 origin) : light(light), origin(origin) {}

	/*
	* @brief 获取 direction 对应的概率密度
	* @param direction 随机方向
	* @return 概率密度
	*/
	virtual double value(const Vec3& direction) const override;

	/*
	* @brief 生成随机方向
	*/
	virtual Vec3 generate() const override;

private:
	Point3 origin;
	Ref<Object> light;
};

double PDF_hit::value(const Vec3& direction) const {
    return light->pdf_value(origin, direction);
}

Vec3 PDF_hit::generate() const {
    return light->random(origin);
}

对光源的修改：RectXZ

double RectXZ::pdf_value(const Point3& origin, const Vec3 direction) const {
    HitInfo info;
    if (this->hit(Ray(origin, direction), 1e-3, INFINITY, info)) {
        double area = (x2 - x1) * (z2 - z1);
        double distance_squared = info.t * info.t * direction.length_squared();
        double cosine = fabs(direction.dot(info.normal) / direction.length());
        // pdf = distance^2 / (cos_alpha * A)
        return distance_squared / (cosine * area);
    }
    else return 0;
}

Vec3 RectXZ::random(const Point3& origin) const {
    Point3 on_light = Vec3(Random::rand_between(x1, x2), k, Random::rand_between(z1, z2));
    return on_light - origin;
}

8.2 混合概率密度

class PDF_mixture : public PDF {
public:
	/*
	* @brief 等比例混合两个PDF
	* @param pdf1 第一个PDF
	* @param pdf2 第二个PDF
	* @param weight0 pdf1的权重
	*/
	PDF_mixture(Ref<PDF> pdf1, Ref<PDF> pdf2, double weight1);

	/*
	* @brief 获取 direction 对应的概率密度
	* @param direction 随机方向
	* @return 概率密度
	*/
	virtual double value(const Vec3& direction) const override;

	/*
	* @brief 生成随机方向
	*/
	virtual Vec3 generate() const override;


private:
	Ref<PDF> pdf[2];
	double weight1;
};

PDF_mixture::PDF_mixture(Ref<PDF> pdf1, Ref<PDF> pdf2, double weight1) {
	pdf[0] = pdf1;
	pdf[1] = pdf2;
	this->weight1 = weight1;
}

double PDF_mixture::value(const Vec3& direction) const {
	return weight1 * pdf[0]->value(direction) + (1 - weight1) * pdf[1]->value(direction);
}

Vec3 PDF_mixture::generate() const {
	if(Random::rand01() < weight1) return pdf[0]->generate();
	else return pdf[1]->generate();
}

8.3 对GetColor的修改

Color ObjectWorld::GetColor(const Ray& r, int& depth) {
	HitInfo info;

	// 如果碰撞到了, 则根据材质计算反射光线
	// 注意 t_min 需要设置一个很小的值, 否则会出现光线重复与同一个物体相交的情况
	if (this->hit(r, 1e-3, INFINITY, info)) {
		Ray r_out;
		Color emit = info.material->emitted(r, info, info.u, info.v, info.position);
		Color attenuation;
		double pdf;

		if (depth < max_depth && info.material->scatter(r, info, attenuation, r_out, pdf)) {
			Ref<RectXZ> light = New<RectXZ>(213, 343, 227, 332, 554, nullptr);
			Ref<PDF_hit> pdf_hit = New<PDF_hit>(light, info.position);
			Ref<PDF_cos> pdf_cos = New<PDF_cos>(info.normal);
			PDF_mixture pdf_mixture(pdf_hit, pdf_cos, 0.8);

			r_out = Ray(info.position, pdf_mixture.generate(), r.Time());
			pdf = pdf_mixture.value(r_out.Direction());
			return emit + attenuation * info.material->scatter_pdf(r, info, r_out) * GetColor(r_out, ++depth) / pdf;		
		}
		else
			return emit;
	}
	// 如果不相交, 则返回黑色
	else {
		return Color(0);
	}	
}