计算机图形学
Chanpter 0:Introduction
三个重要的属性:
- 形状
- 外表
- 动态行为的属性(如粗糙度、移动)
三个基础任务:
- 建模
- 模拟物体的行为
- 渲染Rendering
Visual Computer:
- Image Processing:Image=>Image
- Computer Vision:Image=>3D
- Computer Graphics:3D=>3D,3D=>Image
Chapter 1 2D Graphics
1.1 Rasterization光栅化
- 将二维基本体(primitives,如直线、多边形)转换为光栅图像
- PWM:控制元件一段时间亮,一段时间不亮,以得到不同光强的光
1.1.1 坐标系
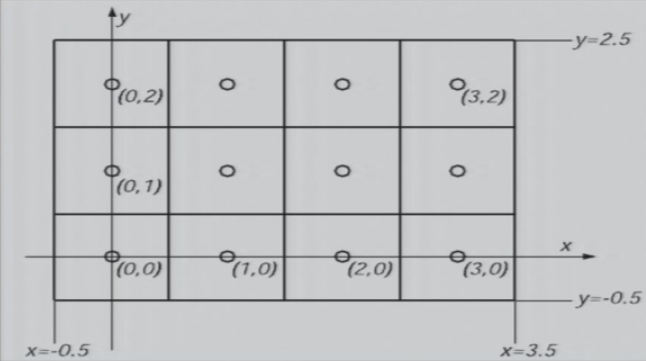
- 坐标系:以像素的中心作为整数坐标
1.2 线段
1.2.1 线段的定义
- 线段:给定起点、终点、以及各自的颜色、线段的颜色
- 一般来说,起点和终点均为整数坐标
1.2.2 线段的光栅化
将线段光栅化到屏幕的要求:
- 选中的像素尽可能接近理想线段
- 像素的序列尽可能直
- 像素的亮度尽可能一样
- 像素的起始和结束尽可能精确
- 画的足够快
- 可以画不同宽度的线段
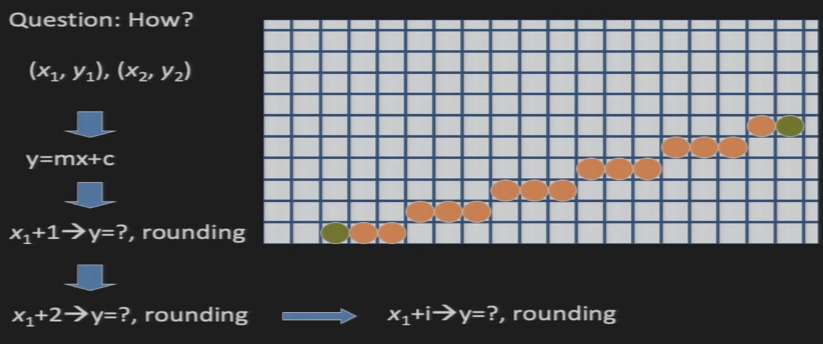
将线段光栅化到屏幕的方法:
- 计算线段的表达式
- 枚举x,计算y,判断计算出的(x,y)属于哪一个像素(Rounding)
- 给对应的像素上色
优化掉Rounding:
- Rounding的任务:四舍五入,本质是做一个比较
- 斜率:x每增加一个单位,y变化相应的单位
DDA:Digital Differential Analyzer,数字微分分析
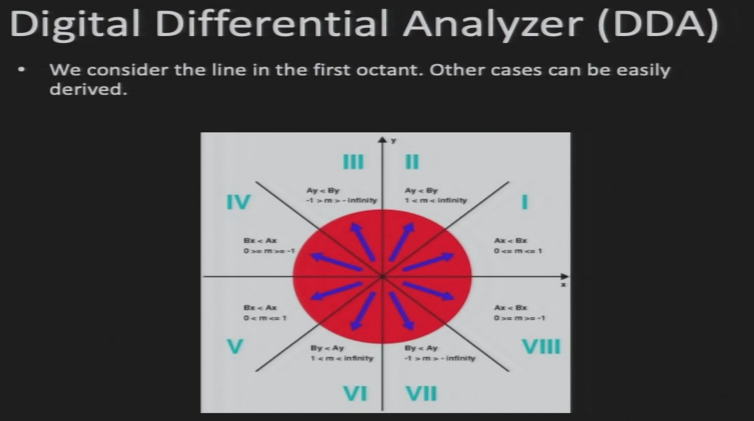
线段的象限:
1.2.3 Bresenham画线算法
\(y_i=m·x_i+c,其中m=\frac{y_2-y_1}{x_2-x_1}\)
思路:
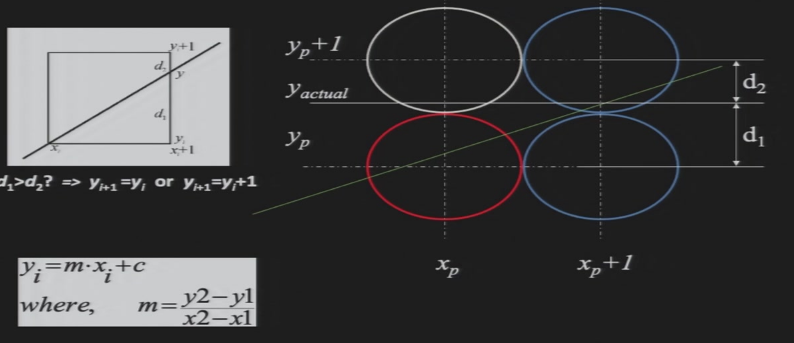
- 对于相邻的两个像素,当x++时,y’只有两种可能:y或y+1
- y’是否+1,取决于\(y_{actual}\)与y+1近,还是y近
Bresenham画线算法:假设线段在第一象限(x增加时y也增加)
定义:\(dx=x_2-x_1,dy=y_2-y_1,m=\frac{dy}{dx}\)
定义:\(y=m(x_i+1)+b,d_1=y-y_i,d2=y_i+1-y\)
若\(d_1-d_2>0\),则\(y_{i+1}=y_i+1\);若\(d_1-d_2<0\),则\(y_{i+1}=y_i\)
定义:\(P_i=(d_1-d_2)*dx=2x_idy-2y_idx+2dy+(2b-1)dx\)
- 由于线在第一象限上,因此\(P_i\)与\(d_1-d_2\)的符号相同
- 因此:若\(P_i>0\),则\(y_{i+1}=y_i+1\);若\(P_i<0\),则\(y_{i+1}=y_i\)
可以计算出,\(P_{i+1}=P_i+2dy-2(y_{i+1}-y_i)dx\)

伪码如下:
plot(x1,y1);
dx = x2 - x1; dy = y2 - y1; P[1] = 2*dy - dx;
for(int i = 1; i < x2+1; i++){
x[i+1] = x[i] + 1;
if(P[i] > 0) y[i+1] = y[i] + 1;
else y[i+1] = y[i];
plot(x[i+1], y[i+1]);
if(P[i] > 0) P[i+1] = P[i] + 2*dy - 2*dx;
else P[i+1] = P[i] + 2*dy;
}
1.3 圆
1.3.1 圆的定义(使用极坐标定义)

\(x_{i+1}=x_i\cos\Delta\theta-y_i\sin\Delta\theta\)
- 存在累加误差
- 一般情况下,浮点加法的误差比浮点乘法的定义大,误差出现在大数加小数上
1.3.2 Bresenham画圆算法
理论推导:
采用八分法画圆:由于圆的对称性,只需要计算出\(\frac{1}{8}\)圆弧的像素点即可

只考虑第一象限的上半部分,x每次增加1,y减少1或不变

将中点\(M(x_i+1,y_i-0.5)\)带入圆的隐式方程,得到:\(d[i]=F(M)=(x[i]+1)^2+(y[i]-0.5)^2-R^2\),如上图所示
- 如果\(d\le0\),则M在圆内,\(p[i+1]=(x[i]+1,y[i])\)
- 如果\(d>0\),则M在圆外,\(p[i+1]=(x[i]+1,y[i]-1)\)
进行递推计算
- 如果\(d[i]\le 0\),得到
- \(d[i]=(x[i]+1)^2+(y[i]-0.5)^2-R^2\)
- \(d[i+1]=(x[i]+2)^2+(y[i]-0.5)^2-R^2\)
- \(\Delta d = 2x[i]+3\)
- 如果\(d[i] > 0\),得到
- \(d[i]=(x[i]+1)^2+(y[i]-0.5)^2-R^2\)
- \(d[i+1]=(x[i]+2)^2+(y[i]-1.5)^2-R^2\)
- \(\Delta d = 2(x[i]-y[i])+5\)
- 如果\(d[i]\le 0\),得到
画圆步骤:
- 画上半部分:
- 输入圆的半径,计算初始值\((x[0],y[0])=(0,R)\)
- 判断\(d[i]\)的符号,计算\((x[i+1],y[i+1])\)的坐标
- \(d[i+1]\)根据\(d[i]\)递推
- 当\(x<y\)时,重复2~3步,否则结束
- 根据对称性,画出完整的圆
1.3.3 椭圆的中点画法
理论推导:
椭圆需要画出\(\frac{1}{4}\),而且我们需要找到分界点,如下图。
- 分界点上,x为主增量
- 分界点下,y为主增量

考虑上半部分:
1. 将中点$M(x[i]+1,y[i]-0.5)$带入椭圆的隐式方程,得到$d[i]=F(M)=a^2(y[i]-0.5)^2+b^2(x[i]+1)^2-a^2b^2$
1. 如果$d\le0$,则M在椭圆内,$p[i+1]=(x[i]+1,y[i])$
2. 如果$d>0$,则M在椭圆外,$p[i+1]=(x[i]+1,y[i]-1)$
2. 进行递推计算
1. 如果$d[i]\le 0$,得到
1. $d[i]=a^2(y[i]-0.5)^2+b^2(x[i]+1)^2-a^2b^2$
2. $d[i+1]=a^2(y[i]-0.5)^2+b^2(x[i]+2)^2-a^2b^2$
3. $\Delta d = b^2(2x[i]+3)$
2. 如果$d[i] > 0$,得到
1. $d[i]=a^2(y[i]-0.5)^2+b^2(x[i]+1)^2-a^2b^2$
2. $d[i+1]=a^2(y[i]-1.5)^2+b^2(x[i]+2)^2-a^2b^2$
3. $\Delta d = b^2(2x[i]+3)+2a^2(-y[i]+1)$对于下半部分:
- 将中点\(M(x[i]-0.5,y[i]+1)\)带入椭圆的隐式方程,得到\(d[i]=F(M)=a^2(y[i]+1)^2+b^2(x[i]-0.5)^2-a^2b^2\)
- 如果\(d\le0\),则M在椭圆内,\(p[i+1]=(x[i],y[i]+1)\)
- 如果\(d>0\),则M在椭圆外,\(p[i+1]=(x[i]-1,y[i]+1)\)
- 进行递推计算
- 如果\(d[i]\le 0\),得到
- \(d[i]=a^2(y[i]+1)^2+b^2(x[i]-0.5)^2-a^2b^2\)
- \(d[i+1]=a^2(y[i]+2)^2+b^2(x[i]-0.5)^2-a^2b^2\)
- \(\Delta d = a^2(2y[i]+3)\)
- 如果\(d[i] > 0\),得到
- \(d[i]=a^2(y[i]+1)^2+b^2(x[i]-0.5)^2-a^2b^2\)
- \(d[i+1]=a^2(y[i]+2)^2+b^2(x[i]-1.5)^2-a^2b^2\)
- \(\Delta d = a^2(2y[i]+3) + 2b^2(-x[i]+1)\)
- 如果\(d[i]\le 0\),得到
- 将中点\(M(x[i]-0.5,y[i]+1)\)带入椭圆的隐式方程,得到\(d[i]=F(M)=a^2(y[i]+1)^2+b^2(x[i]-0.5)^2-a^2b^2\)
画圆步骤:
- 画上半部分:
- 输入椭圆的半径,计算初始值
- \((x[0],y[0])=(0,b)\)
- \(d[0]=a^2(b-0.5)^2+b^2-a^2b^2\)
- 判断\(d[i]\)的符号,计算\((x[i+1],y[i+1])\)的坐标
- 如果\(d\le0\),则M在椭圆内,\(p[i+1]=(x[i]+1,y[i])\)
- 如果\(d>0\),则M在椭圆外,\(p[i+1]=(x[i]+1,y[i]-1)\)
- \(d[i+1]\)根据\(d[i]\)递推
- 如果\(d[i]\le 0\),得到\(d[i+1] = d[i] + b^2(2x[i]+3)\)
- 如果\(d[i] > 0\),得到\(d[i+1] = d[i] + b^2(2x[i]+3)+2a^2(-y[i]+1)\)
- 当\(2a^2(y[i]-0.5)>2b^2(x[i]+1)\)时,重复2~3步,否则结束
- 输入椭圆的半径,计算初始值
- 画下半部分:
- 输入椭圆的半径,计算初始值
- \((x[0],y[0])=(a,0)\)
- \(d[0]=a^2+b^2(a-0.5)^2-a^2b^2\)
- 判断\(d[i]\)的符号,计算\((x[i+1],y[i+1])\)的坐标
- 如果\(d\le0\),则M在椭圆内,\(p[i+1]=(x[i],y[i]+1)\)
- 如果\(d>0\),则M在椭圆外,\(p[i+1]=(x[i]-1,y[i]+1)\)
- \(d[i+1]\)根据\(d[i]\)递推
- 如果\(d[i]\le 0\),得到\(d[i+1] = d[i] + a^2(2y[i]+3)\)
- 如果\(d[i] > 0\),得到\(d[i+1] = d[i] + a^2(2y[i]+3) + 2b^2(-x[i]+1)\)
- 当\(2a^2(y[i]-0.5) \le 2b^2(x[i]+1)\)时,重复2~3步,否则结束
- 输入椭圆的半径,计算初始值
- 根据对称性,画出完整的椭圆
1.4 多边形填充
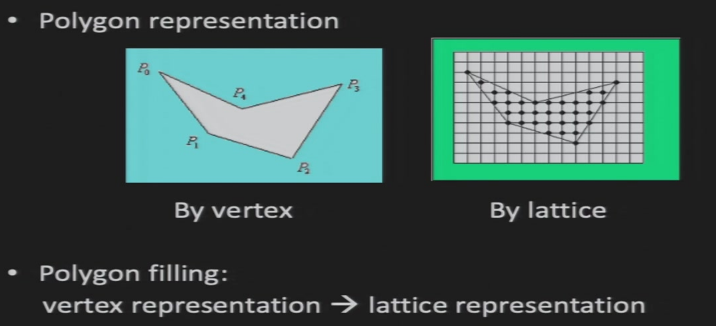
1.4.1 判断一个点是否在多边形之中
奇偶测试:画水平线,与多边形相交,奇数点和偶数点之间的像素在多边形之中
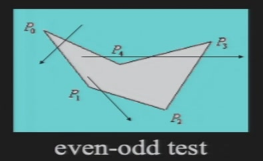
Winding Number test:从选定的点开始,计算与多边形的所有相邻顶点之间的夹角,如果在内部,则夹角和为360°
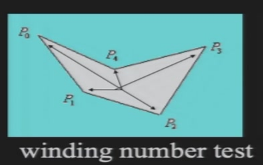
1.4.2 Scan-line Method

从上到下,从左到右,进行扫描
计算每一根扫描线与多边形的交点,奇数点与偶数点之间填充颜色
计算交点:假设交点数不发生变化,则这就是画线算法的一步

1.4.3 Seed Fill Algorithm种子填充算法

1.4.4 Clipping
Clipping:将不在屏幕中的对象裁剪掉
- 在光栅化之前进行,对primitive进行操作
Chapter 2:Introduction to OpenGL
2.1 OpenGL的功能
- 定义物体的形状、材质的属性、光照
- 根据简单的点、线、多边形构建一个复杂的图形
- 将物体放到场景中,且投射到摄像机中
- 将物体的数学表达式转化为像素:Rasterization
- 计算物体的每个点的颜色:Shading
2.2 OpenGL工具链
- OpenGL < GL/gl.h >:跨平台的核心库
- GLU < GL/glu.h >:实现了一系列的图形函数
- GLUT < GL/glut.h >:实现了窗口创建、操作系统调用(如鼠标、键盘)
- GLUI:用户界面
2.3 OpenGL中的三个阶段
- 在世界坐标中定义一个物体
- 设置Modeling & Viewing变换
- 渲染场景
2.4 OpenGL的工作方式
- OpenGL是一个状态机
- OpenGL会给定一个起始状态,有一些初始值
- 除非显式设置一些值,否则当前状态不会改变
- 比如设置当前颜色是红色,在下一次显式更改颜色之前,所有的图形均会化成红色
- 所有的状态均有一个默认值
2.5 OpenGL的元素
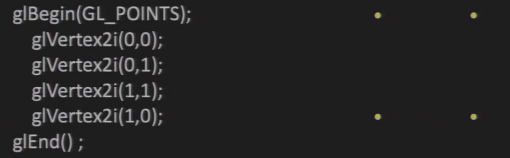
GL_POINTS:点
GL_LINES:线
- 给定一个点的数组,两两之间画线

GL_LINE_STRIP:线
- 给定一个数组,每一根线段的起点是前一根的终点,中点是后一根的起点

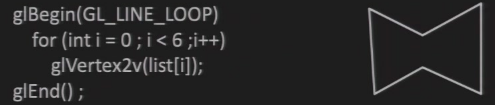
GL_LINE_LOOP
- 线,给定一个数组,每一根线段的起点是前一根的终点,中点是后一根的起点
- 首尾相连
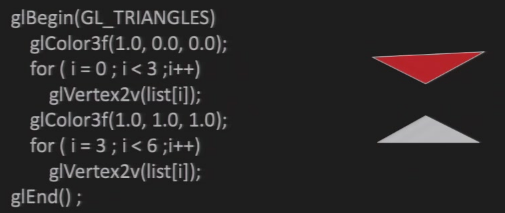
GL_TRIANGLES:三角形
- 给定一个点的数组,以三个为一组画三角形
GL_TRANGLE_FAN:三角形
- 给定一个点的数组,第0个点为扇形的圆心,剩下的逆时针排列
GL_TRANGLE_STRIP:三角形
- 给定一个点的数组,相邻两个三角形共边
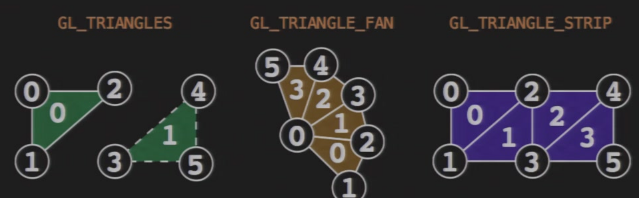
GL_POLYGON:多边形
- 多边形默认是共面、凸多边形

GL_QUADS:四边形
GL_QUAD_STRIP:四边形
2.6 OpenGL的基础格式
2.6.1 OpenGL的函数
所有的函数名以gl开始
glVertex3f(0.0, 1.0, 1.0);
常量均为大写
GL_COLOR_BUFFER_BIT
3. 数据类型以**GL**开始:为了跨平台
```c++
GLfloat onevertex[3]大多数函数名的结尾表示参数的数据类型及个数
glVertex3f(...); //3个GLfoat的参数
glVertex:所有的对象都是由顶点定义的
glVertex2f(x, y);
glVertex3f(x, y, z);
glVertex4f(x, y, z, w);
glVertex3fv(a); // with a[0], a[1], a[2]
2.6.2 根据顶点创建物体
glBegin(GL_POLYGON); |
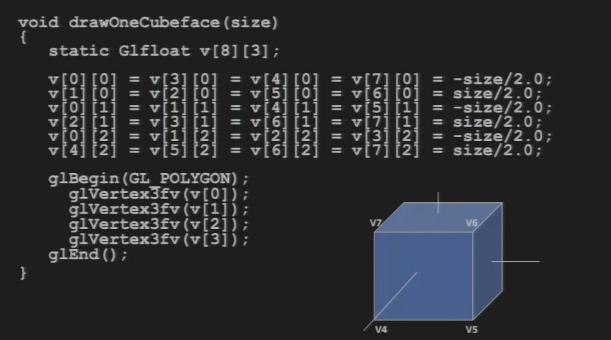
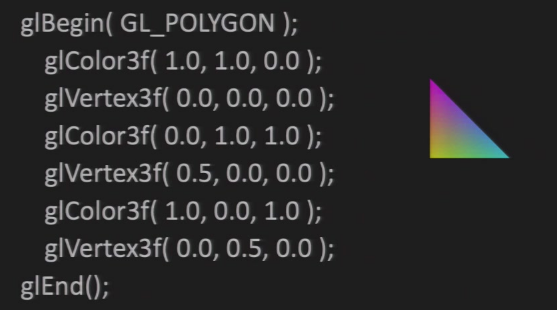
2.6.3 颜色
- 根据RGB三个分量,float类型,范围为[0.0, 1.0]
// 背景颜色 |
2.6.4 其它可以放在glBegin/glEnd中的函数

2.6.5 多边形的显示模型
2.6.6 编译OpenGL程序
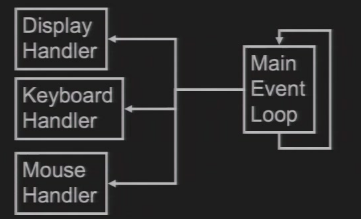
2.6.7 GLUT-based程序的结构
GLUT基于用户定义的回调函数,在每一个事件发生时调用
用户显示屏幕的函数
用于重新设置viewport的大小的函数
用于处理键盘/鼠标输入的函数
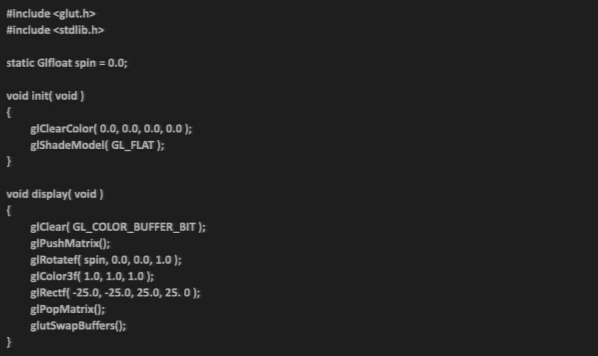
例:画一个多边形
int main(int argc, char *argv[]){
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_RGBA | GLUT_DOUBLE);
int windowHandle = glutCreateWindow("Simple GLUT App");
glutDisplayFunc(redraw);
glutMainLoop();
return 0;
}
void readraw(){
glClear(GL_COLOR_BUFFER_BIT);
glBegin(GL_QUADS);
glColor3f(1, 0, 0);
glVertex3f(-0.5, 0.5, 0.5);
glVertex3f( 0.5, 0.5, 0.5);
glVertex3f( 0.5, -0.5, 0.5);
glVertex3f(-0.5, -0.5, 0.5);
glEnd();
glutSwapBuffers();
}Double buffer:画在一个buffer中,显示另一个buffer,然后进行切换
- 可以防止显示绘画的过程
其它GLUT

2.6.8 回调
Reshape Callback

鼠标回调

键盘回调

静止回调
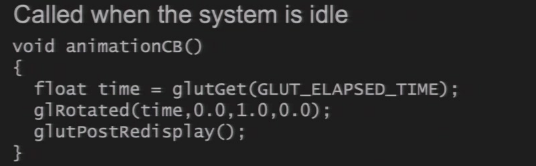
菜单回调
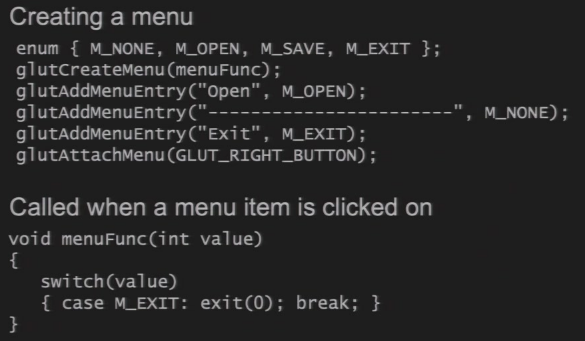
2.6.9 动画


Chapter 3:Basic Math
3.1 向量
3.1.1 点乘
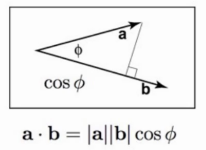
\(\vec{a}·\vec{b}=|\vec{a}||\vec{b}|\cos\theta=x_a*x_b+y_a*y_b+z_a*z_b\)
本质是:投影操作
- 函数可以看作是一个无限维的向量
- FFT本质上是将函数换了一个坐标轴(不同的余弦函数),进行投影操作
转换坐标:
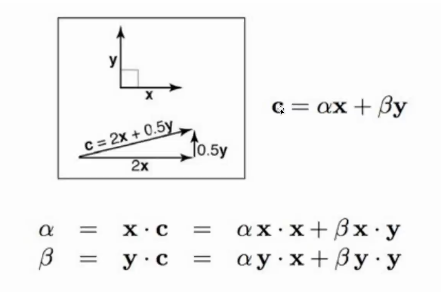
3.1.2 差积
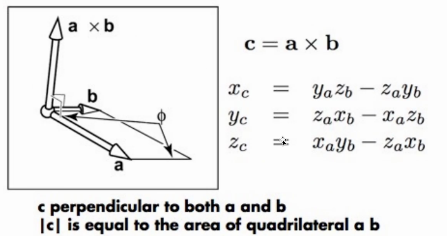
- 方向:右手法则(从\(\vec{a}\)转到\(\vec{b}\))
3.1.3 点的操作
- 点 - 点 = 向量
- 点 + 向量 = 点
3.2 直线
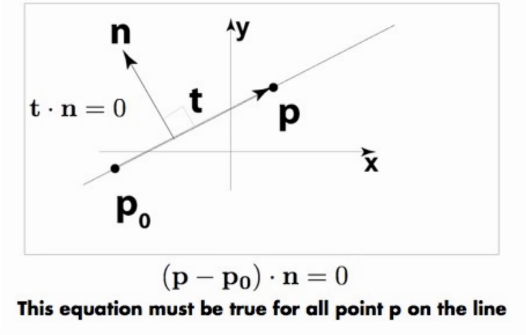

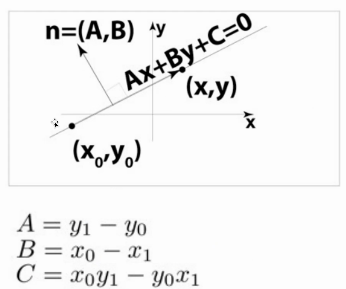
- 直线方程:\((p-p_0)·\vec{n}=0 \rightarrow
ax+by+c = 0\)
- \(\vec{t} = p-p_0=(x_1-x_0,y_1-y_0)\)
- \(\vec{n}=Prep(\vec{t})=(y_0-y_1,x_1-x_0)\)
void LineEquation(vertex &v0, vertex &v1, line &l){ |
3.3 变换Transform
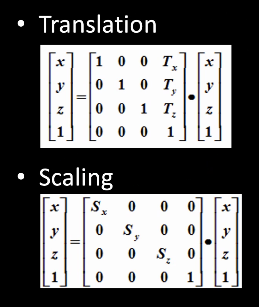
3.3.1 平移Translation
\[ x\rightarrow x+T_x \\ y\rightarrow y+T_y \\ z\rightarrow z+T_z \\ \]
- 刚体变换:不会改变物体的形状
3.3.2 缩放Scaling
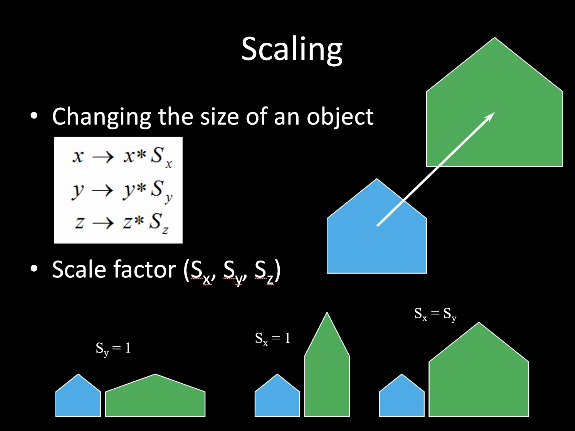 \[
x\rightarrow x*S_x \\
y\rightarrow y*S_y \\
z\rightarrow z*S_z \\
\]
\[
x\rightarrow x*S_x \\
y\rightarrow y*S_y \\
z\rightarrow z*S_z \\
\]
- 以原点为中心进行缩放:直接对xyz乘上对应的缩放因子
- 以某个点为中心进行缩放:先平移到原点,然后缩放,然后再平移回去
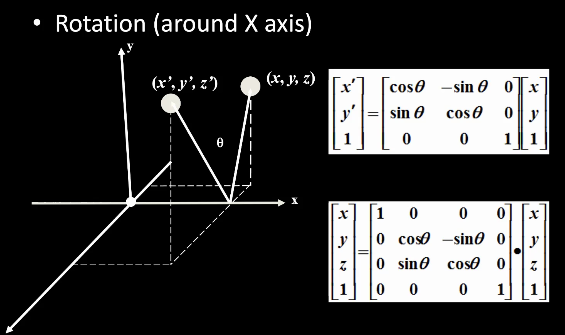
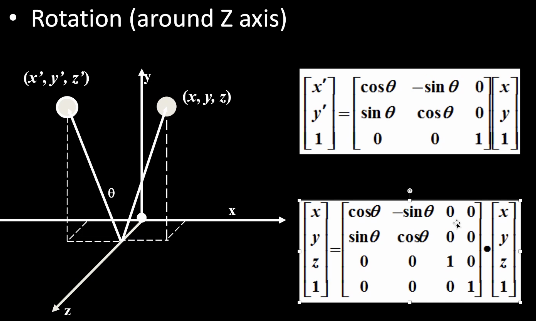
3.3.3 旋转Rotation
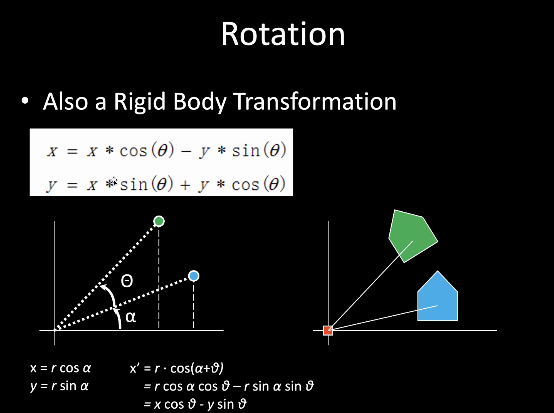 \[
x'=x*\cos\theta-y*\sin\theta \\
y'=x*\sin\theta+y*\cos\theta \\
\]
\[
x'=x*\cos\theta-y*\sin\theta \\
y'=x*\sin\theta+y*\cos\theta \\
\]
- 刚体变换:不会改变物体的形状
- 2维:绕原点旋转;3维:绕旋转轴旋转
 \[
x'=x_r+(x-x_r)\cos\theta-(y-y_r)\sin\theta \\
y'=y_r+(y-y_r)\cos\theta+(x-x_r)\sin\theta \\
\]
\[
x'=x_r+(x-x_r)\cos\theta-(y-y_r)\sin\theta \\
y'=y_r+(y-y_r)\cos\theta+(x-x_r)\sin\theta \\
\]
- 绕某一个点旋转:
- 将要旋转的点平移到原点上
- 进行旋转
- 然后再平移回去
3.3.4 剪切Shearing

3.4 齐次坐标
3.4.1 点/向量的对应关系
- 点:\([x,y]\rightarrow[x,y,1]\)
- 向量:\([x,y]\rightarrow[x,y,0]\)
- \([x,y,w]==[x/w,y/w,z/w]\)
3.4.2 线性变换与矩阵的对应关系

3.4.3 复合变换
- 每乘一个矩阵,就相当于进行了一次变换
- 由于矩阵乘法具有结合律,因此可以先将变换矩阵相乘,再和向量相乘
- 也就是说,可以用一个矩阵,表示任意的齐次变换
- 先进行的变换,其变换矩阵写在后面

3.4.4 矩阵形式表示关于某个点P的变换


3.4.5 绕任意轴旋转

将旋转轴旋转到Z轴
- \(T\):将轴平移至过原点
- \(R_x(\alpha)\):绕X轴旋转,让旋转轴处于yz平面
- \(R_y(\beta)\):绕Y轴旋转,让旋转轴处于xz平面
- \(R_z(\theta)\):绕Z轴旋转,让旋转轴与z轴重合
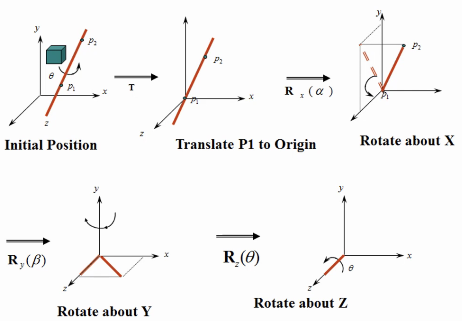
绕Z轴旋转角度
进行第1步的逆变换
3.5 OpenGL中的变换
3.5.1 CTM
- Current Transform Matrix:当前变换矩阵
3.5.2 修改CTM

3.5.3 绕某个轴轴旋转

- 最后写的操作会最先执行,按照前面写矩阵的顺序写代码即可
3.5.4 Matrix Stack

3.6 向量的进一步应用
3.6.1 计算两个线段的交点
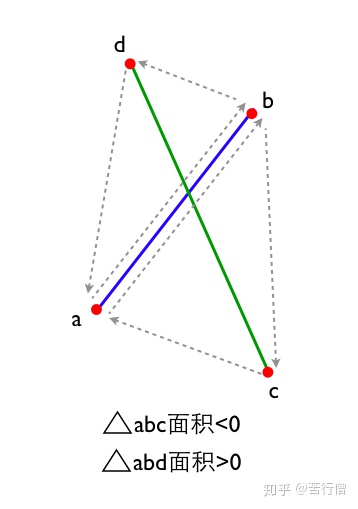
判断两个线段相交
- 判断依据:点c和点d在直线ab的两侧,且点a和点b在直线cd的两侧
- 判断方法:使用向量叉乘求abd, abc的“面积”,当两线段相交时,abc与abd面积正负号相反
// 以ab为三角形公共边,求三角形abc, abd的面积,并判断是否不相交
double area_abc = (a.x - c.x) * (b.y - c.y) - (a.y - c.y) * (b.x - c.x);
double area_abd = (a.x - d.x) * (b.y - d.y) - (a.y - d.y) * (b.x - d.x);
if (area_abc * area_abd >= 0) return false;
// 以cd为三角形公共边,求三角形abc, abd的面积,并判断是否不相交
double area_cda = (c.x - a.x) * (d.y - a.y) - (c.y - a.y) * (d.x - a.x);
double area_cdb = area_cda + area_abc - area_abd ;
if (area_cda * area_cdb >= 0) return false;计算交点
double t = area_cda / ( area_abd - area_abc );
double dx = t * (b.x - a.x),
double dy = t * (b.y - a.y);
intersect_p.x = a.x + dx;
intersect_p.y = a.y + dy;
Chapter 4:Viewing in 2D & 3D
4.1 2D中的Viewing
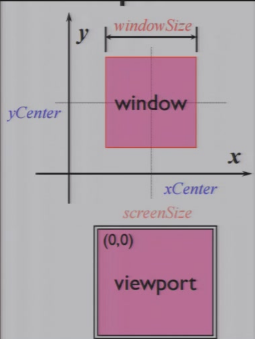
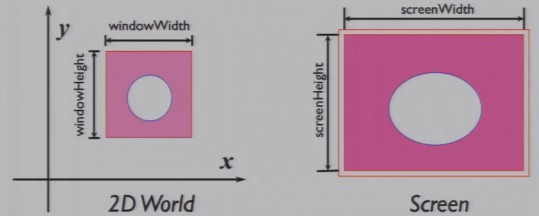
4.1.1 Window
- Window:一个2D世界中的矩形区域
- 中心:(xCenter, yCenter)
- 大小:windowSize
- Screen / Viewport:一个像素点的矩阵
- 大小:screenSize,以像素为单位
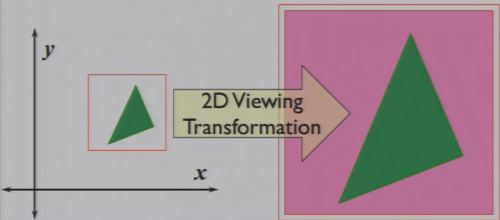
4.1.2 2D Viewing Transformation
- 将2D世界中能够看到的部分window映射到屏幕viewport上
- 也成为:window-to-viewport transformation
4.1.3 Derivation推导
| 先平移到坐标原点,并且进行相应缩放 | 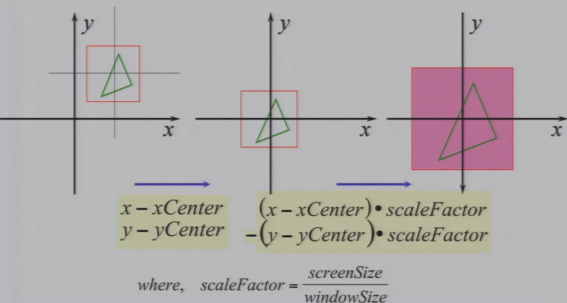 |
|---|---|
| 然后将坐标轴转化为屏幕的坐标 | 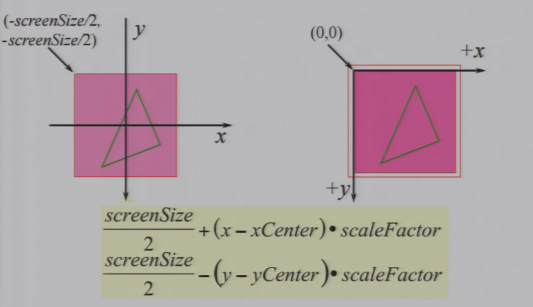 |
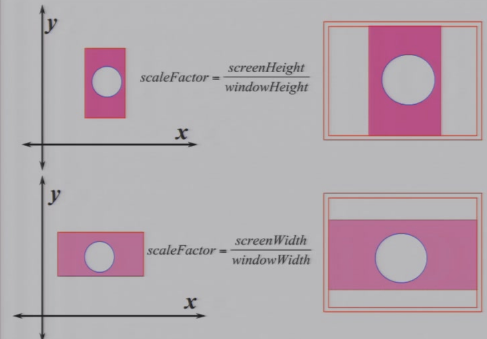
4.1.4 Aspect Ratio纵横比
4.1.5 OpenGL中的命令
// 设置视口: 最终图像映射到的像素矩阵 |

4.1.6 Modeling vs Viewing
- Modeling Transformation:修改场景
- Viewing Transformation:修改视窗位置,不会修改场景
4.2 3D中的Viewing
4.2.1 透视投影 Perspective Projection
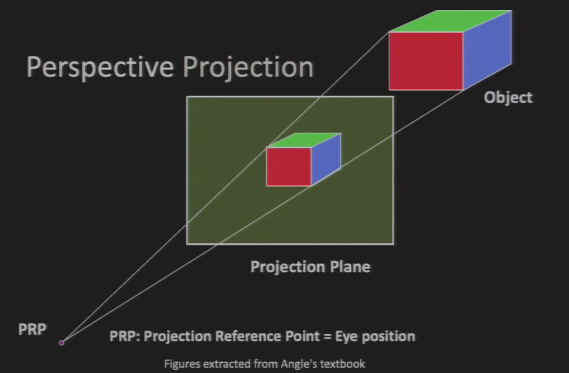
- 所有点的延长线交于一点
- PRP:Projection Reference Point,投影参考点
- 也就是眼睛所在位置
- 投影大小 与 距离、朝向 都有关系
4.2.2 平行投影 Parallel Projection
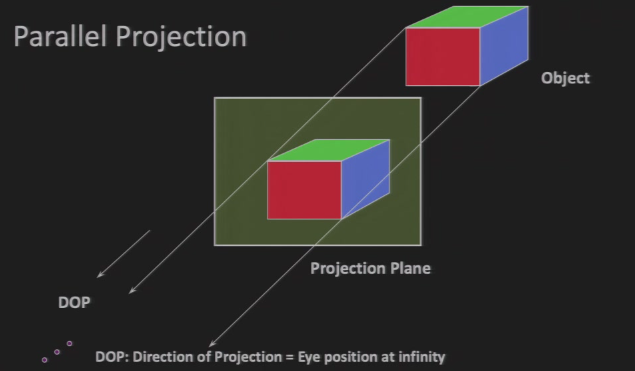
对应点连线相互平行
- DOP:Direction of Projection,投影方向
- 相当于眼睛在无穷远的位置
投影大小 只与 朝向 有关系
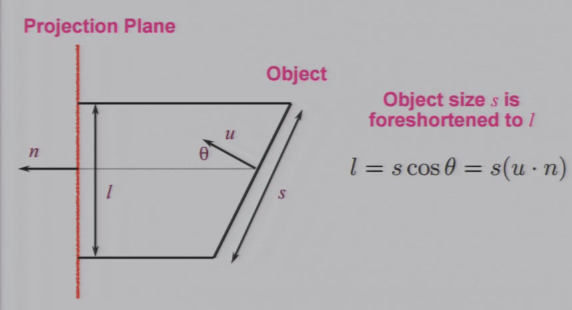
斜平行投影
- 最一般的平行投影
- 平行与投影平面的角度、大小不变
- 不平行投影平面的会被拉伸
4.3 View Specification
4.3.1 定义一个相机
Reference:相机的位置
view-direction(vrp):相机的朝向
up-direction(upVector):相机的向上方向
- 保证与view-direction垂直
- 一般是指定一个朝天的方向sky-vector
- 然后找最接近朝天方向的垂直于相机朝向的向量
- 计算方法:
- sky-vector × view-direction,得到right-vector
- right-vector × view-direction,得到up-vector
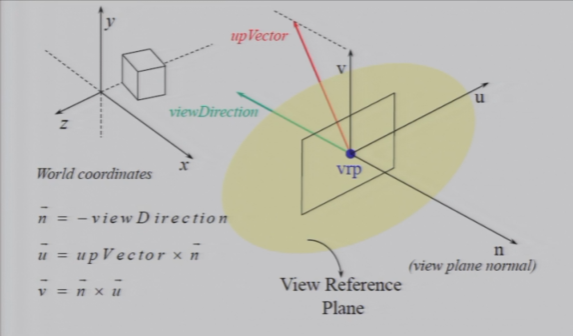
4.3.2 World-to-View Transformation
- 先将相机的坐标轴 平移到 原点
- 然后将相机的坐标轴 投影到 原坐标轴
4.3.3 平行投影

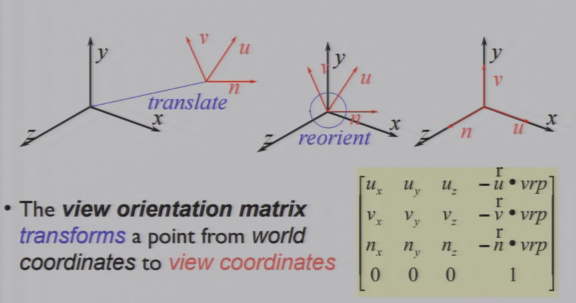
- 先进行World-to-View Transformation
- 然后进行平行投影:直接舍弃Z轴
- 最后进行2D viewing transformation

4.3.4 透视投影
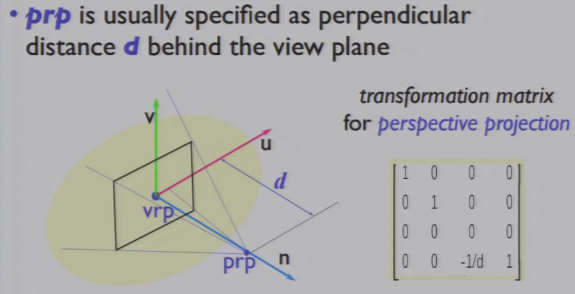
- 先进行World-to-View Transformation
- 然后进行透视投影:乘投影矩阵
- 最后进行2D viewing transformation

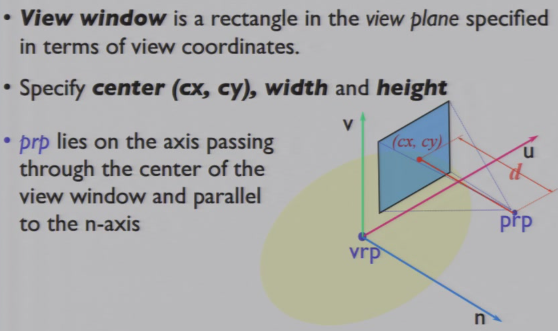
4.3.5 View Window
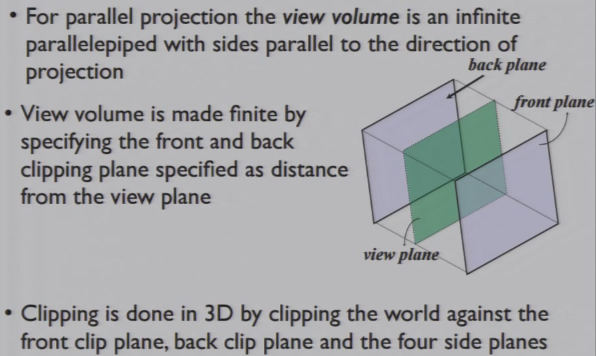
4.3.6 View Volume
只有front plane和back plane之间的物体才能被看见
透视投影:金字塔型
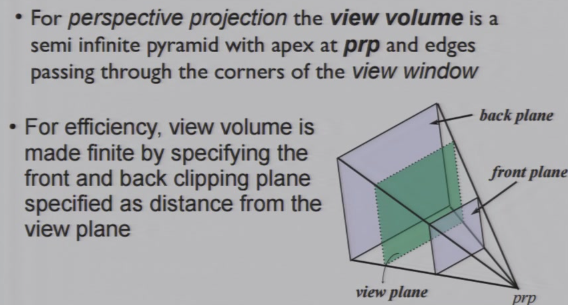
平行投影:长方体型
4.3.7 完整的View Specification
- 定义世界坐标系
- position of viewing:vrp
- direction of viewing:-n
- up direction for viewing:upVector
- 定义视角坐标系
- view window:center(cx, cy), width, height
- prp:distance from the view plane
- front clipping plane:distance from view plane
- back clipping plane:distance from view plane
4.4 OpenGL编程
问题:如何处理Back-face Culling无法解决的面
回答:将相机所在的顶点与面上的点连线,与相机朝向向量点乘,判断向量的模
Chapter 5:Hidden Surface Removal & Antialiasing
5.1 获得真实的渲染效果
5.1.1 要求
- 透视投影的视图
- 适当剪裁的视场
- 隐藏看不到的部分
- 表面细节,如纹理等
- 光照细节,如阴影等
- 体积效应,如透过水、蒸汽、烟等分离介质的透明度和半透明性
- 动态效果,如运动等
5.1.2 相关OpenGL函数
glEnable / glDisable(GL_CULL_FACE); |
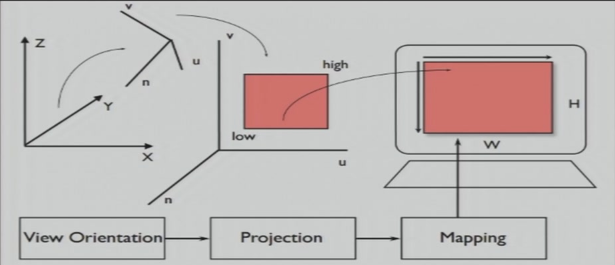
5.1.3 View流水线
5.2 可视表面确定
目标:
- 给定一组3D对象和视图规范,
- 确定当沿投影方向观看时,对象的那些部分是可见的
- 或者,等价地,消除隐藏部分(隐藏线和表面)
- 可见部分将用适当的阴影绘制/显示
方法:
- 对象空间算法
- 对象精度
- 图像空间算法
- 图像精度
- Z-缓冲区
5.3 Back-face Culling
在一个封闭的多边形表面,如多面体或实心多面体的表面,
- 其法线点远离观察者的面是不可见的,
- 这样的背面可以在进一步的处理中消除
这种方法被称为Back-face Culling
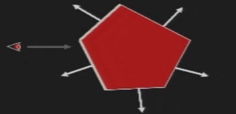
Back Face:
- 物体表面的一部分背对眼睛
- 即法线指向远离眼睛的表面
计算方法:
- 面的法向量 与 观察方向向量 点乘
- 负数表示朝向观察者
- 正数表示远离观察者
Back-face Culling的不足
- 无法判断物体之间的遮挡关系
- 背面一定看不到,前面不一定能看到
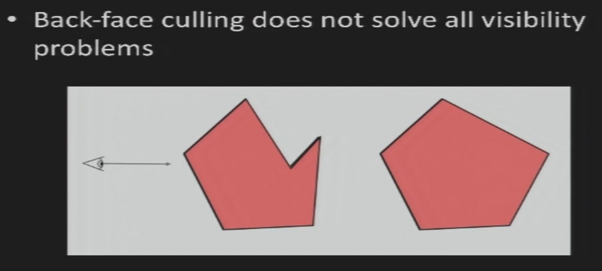
Back-face Culling结果成立的情况:
- 单个、闭合的、凸多边形
5.4 Painter’s Algorithm
5.4.1 算法
- 物体从远到近排序,先画远的,后画近的,自动形成遮挡
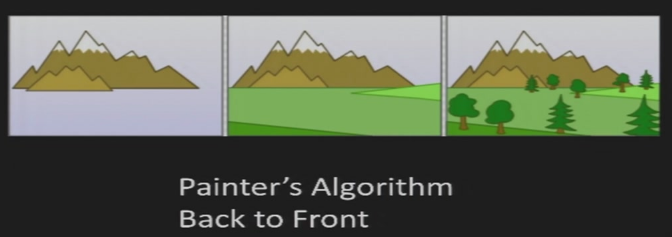
缺点:
有的图形不可被排序

解决方法:
- 将物体进行切割,然后进行排序
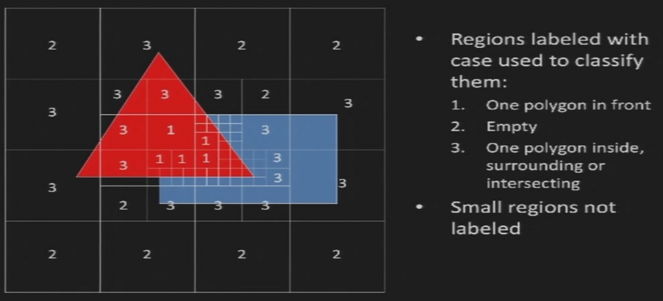
5.4.2 Warnock’s Area Subdivision
- 从整个图像开始
- 如果满足以下情况之一,则直接进行绘制
- 在前面的多边形覆盖整个窗口
- 有最多一个多边形在窗口
- 否则将窗口分为4个部分,并且重复这两步
- 如果区域是单像素的,选择深度最小的表面
- 优点:
- 不过度渲染,抗锯齿性好
- 进一步获取亚像素信息
- 缺点:
- 测试相当复杂和缓慢
- 不适合硬件实现
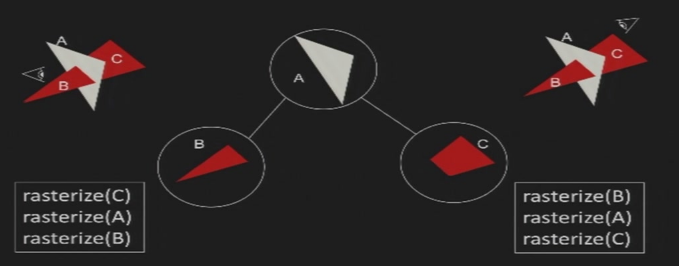
5.4.3 BSP树
BSP:Binary Space Partitioning Trees
构建BSP树
- 选择一个切割面,将空间分为两部分
- 切割面为根节点,靠近观察者的是左子结点,远离观察者的是右子结点
- 所有与切割面相交的三角形,会被分解为两个多边形
- 判断需要切割:三个顶点带入平面方程,符号不一样
- 切割方法:二分三角形,每一步舍去在平面同一方向的多边形
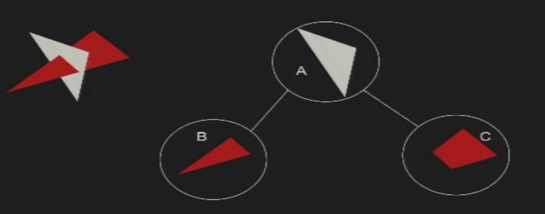
- 选择一个切割面,将空间分为两部分
绘制
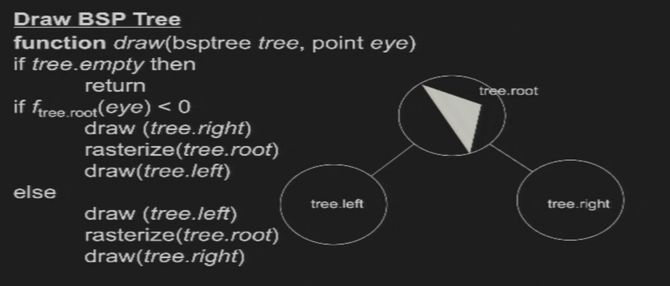
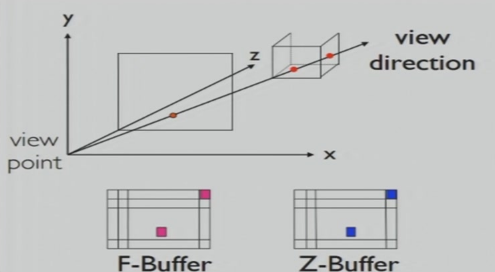
5.5 Z-buffer Algorithm
5.5.1 算法
- 在记录颜色信息的F-Buffer之外,添加一个大小相同的Z-Buffer,存储深度(Z)信息
- 深度的计算:相机朝向向量 与 面 交点的Z值
- 优点:绘画的顺序不影响最后的结果
for(j = 0; j < SCREEN_HEIGHT; j++) |
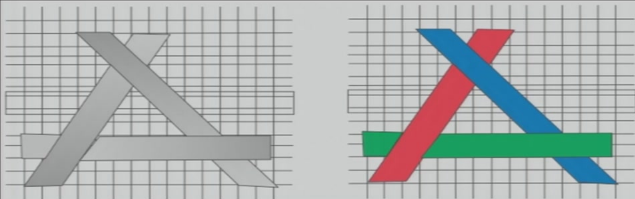
5.5.2 示例
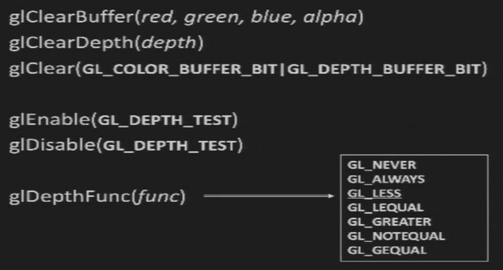
5.5.3 相关OpenGL函数
5.6 Ray Casting
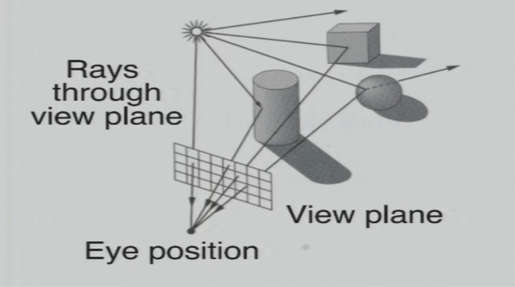
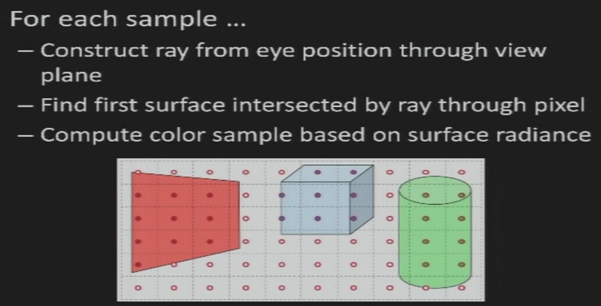
5.7 Aliasing 锯齿/混叠
Aliasing是由于显示设备的离散特性造成的
栅格化就像用一组有限的值对连续信号进行采样
如果采样率不充分,信号就会丢失,这种抽样误差称为Aliasing
Aliasing的效果:
- 锯齿状边缘
- 渲染不正确的细节
- 可能会漏掉小物件
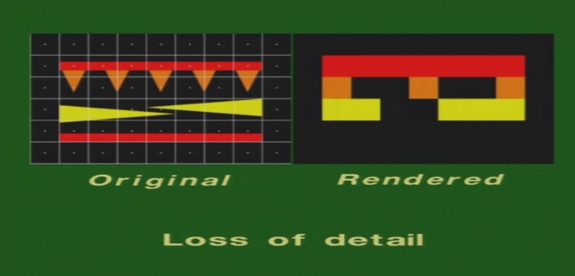
5.7.1 Super-sampling
- 每一个像素,采样多个点,进行平均,作为当前像素的颜色

5.7.2 Area-sampling


http://www.pbrt.org/chapters/pbrt_chapter7.pdf
Chapter 6:Color Theory & Programmable Pipeline
6.1 什么是颜色
- Color是大脑对特定视觉刺激的反应
- 知觉:观察者锁经历的主观感受,没有观察者就没有颜色
- 颜色取决于:
- 光的物理特性
- 光与物理材料的相互作用
- 人类的视觉系统和大脑对由此产生的现象的解释
6.2 光的物理特性
- 光是一种难以观测的动态现象
- 现在的研究正在试图对光进行建模
- 目前,物理学家提出了两种模型来解释光的行为
- 波模型,将光视为水波
- 粒子模型,该模型假设光是由微小的、不可见的振动粒子—光子构成的
6.2.1 光的粒子模型
从颜色的角度来看,采用了粒子模型
当光子沿着直线运动时,它们会以特定的频率振动
假设光子携带一定的能量,能量与它们的振动频率成正比,\(E = h f\)
- \(h\)是普朗克常数
- \(f\)是振动的频率
光子的行为是循环的,有一个重复的模式
光子从一个周期开始到下一个周期开始所经过的距离称为波长,\(\lambda=\frac{c}{f}\)
- \(c\)是光速
- \(f\)是频率
每个光子都有一个与其相关的波长,光的颜色取决于这个波长
光的强度取决于存在的光子的数量
光是一种连续的电磁光谱
- 粒子数在波长上的分布

6.2.2 计算光在脑中产生的电信号
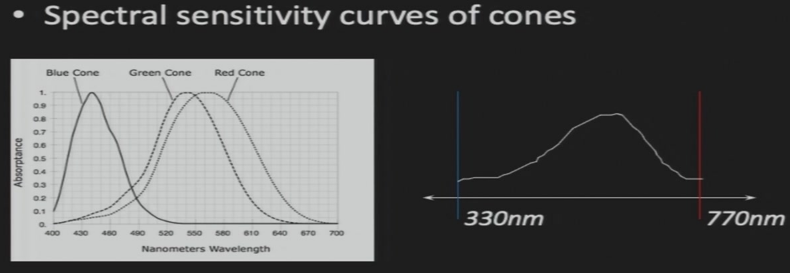
\(r=\int f(x)s(x)dx\)
- \(f(x)\):光强沿波长分布函数(右图)
- \(s(x)\):人眼细胞敏感度沿波长分布函数(左图)
- 两个函数乘积再积分 ==> 卷积 ==> 离散化之后,变为向量的点乘 ==> \(f(x)\)在\(s(x)\)上的投影
6.3 颜色模型
RGB:加色模型,从黑色开始添加颜色
- Red / Green / Blue
CMYK:减色模型,从白色出发开始减去颜色
- Cyan / Magenta/ Yellow / Black
HSV:
- Hue(颜色) / Saturation(饱和度) / Value
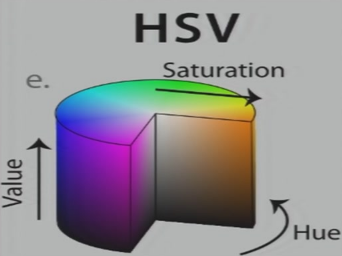
Lab:概念颜色空间
6.4 可编程流水线
6.4.1 可编程图形学流水线
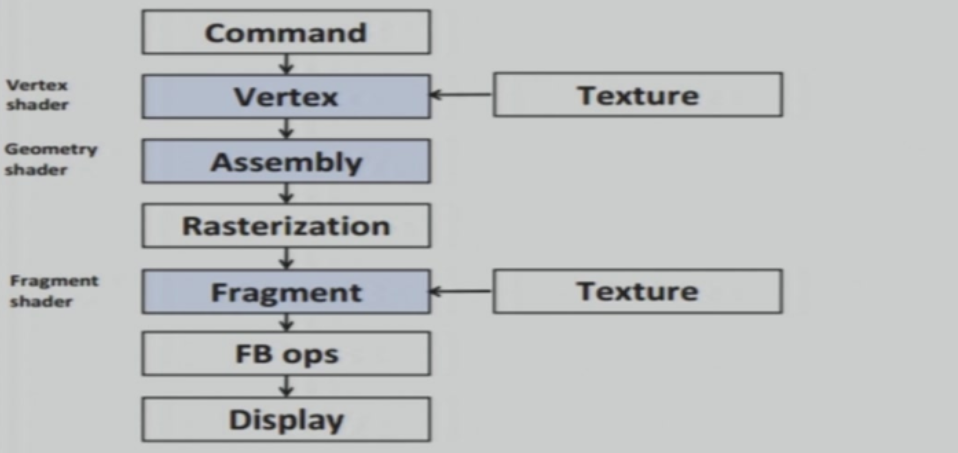
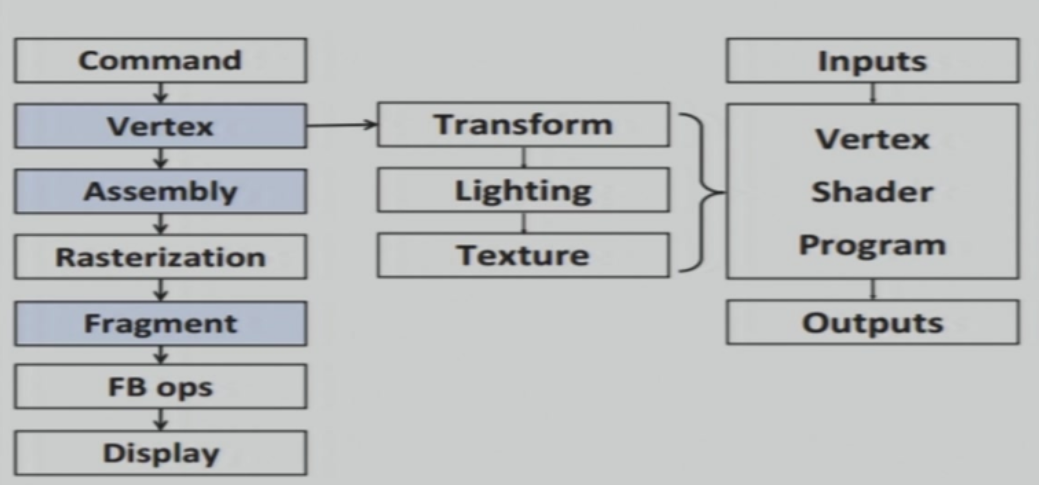
6.4.2 着色器程序结构
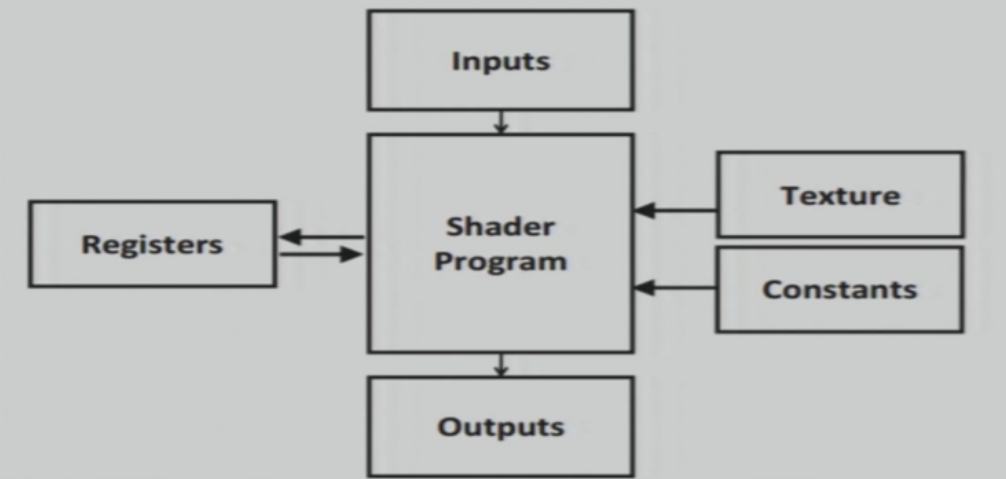
6.4.3 GPU的结构
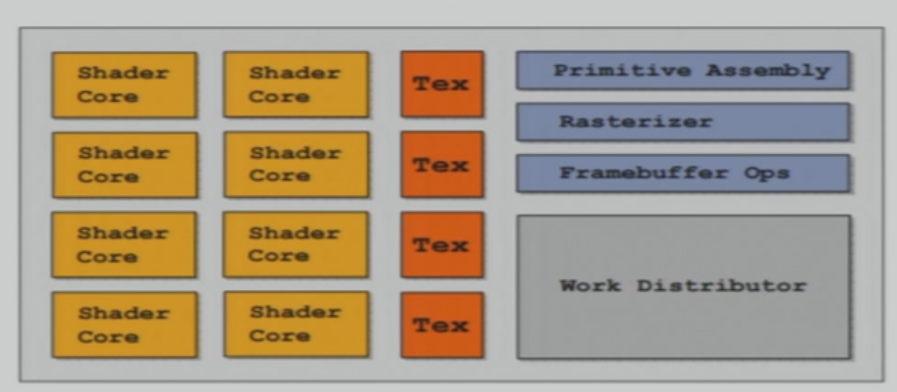
6.5 GLSL
6.5.1 变量
uniform:可以在程序中改变,但在shader中是常量
// OpenGL中预先定义的变量
uniform mat4 gl_ModelViewMatrix;
uniform mat4 gl_ProjectionMatrix;
uniform mat4 gl_NormalMatrix;
// 用户定义
uniform float time;attribute:顶点属性的输入
attribute vec4 gl_Color;
varying vec4 gl_FrontColor;
varying vec4 gl_BackColor;
void main(){
gl_FrontColor = gl_Color;
}varying:顶点属性的输出
6.5.2 向量
// 构造函数 |
6.5.3 纹理
uniform sampler2D someTexture; |
6.5.4 程序与GLSL沟通

6.5.5 顶点着色器

6.5.6 片段着色器

6.5.7 示例
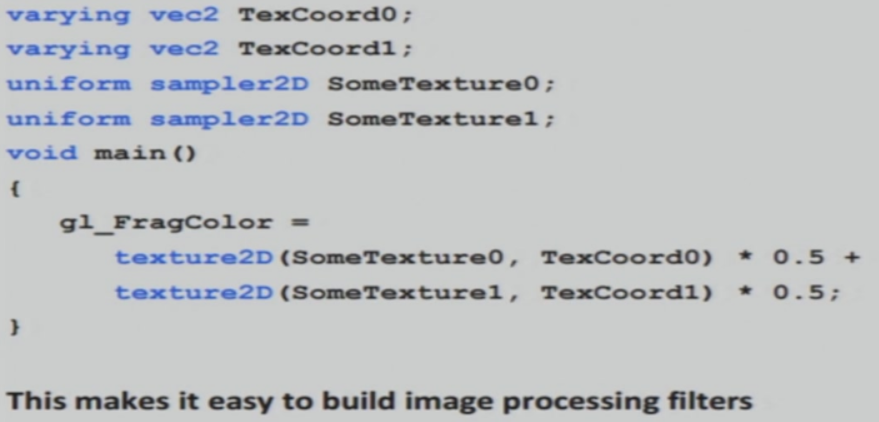
Chapter 7:Curves
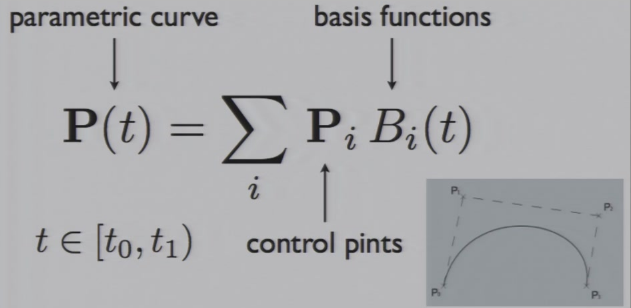
7.1 曲线的表达形式
- 显式曲线:\(y=f(x)\)
- 隐式曲线:\(g(x,y)=0\)
- 参数曲线:\(x=x(t),y=y(t)\)
7.2 隐式曲线 Implicit Curves
优点:很容易判断一个点是在曲线上/里/外
缺点:难以找到所有的点
找点的方法:
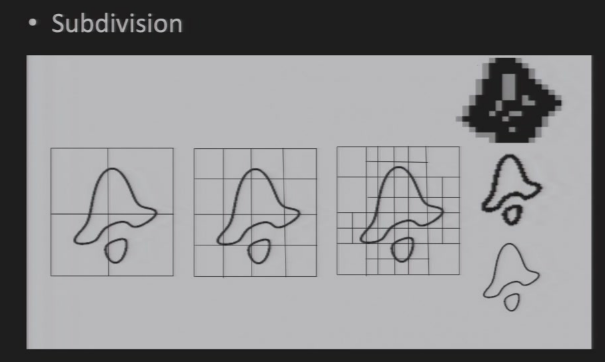
7.3 参数化曲线 Parametric Curves
- \(C = C(u) = [x(u),y(u),z(u)]\)

7.3.1 插值
Nearest Neighbor插值
- 缺点:值不连续

线性插值
- 缺点:导数不连续
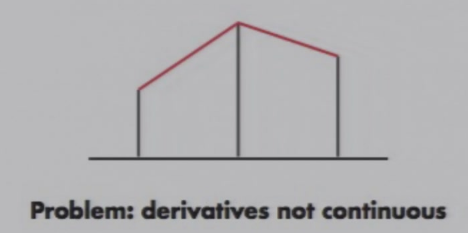
平滑插值
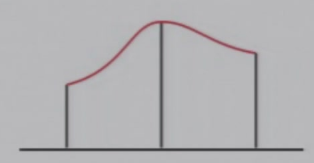
7.3.2 Cubic Hermite插值
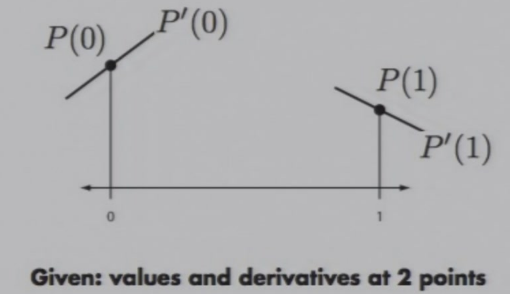
已知:两个值,两个导数
假设一个三次多项式:\(P(t)=at^3+bt^2+ct+d, P'(t)=3at^2+2bt+c\)
- \(P(0)=d,P(1)=a+b+c+d,P'(0)=c,P'(1)=3a+2b+c\)


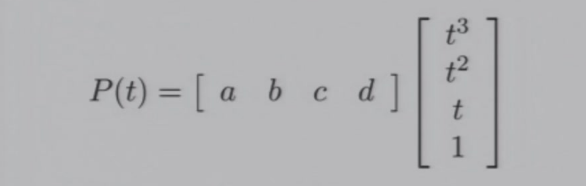
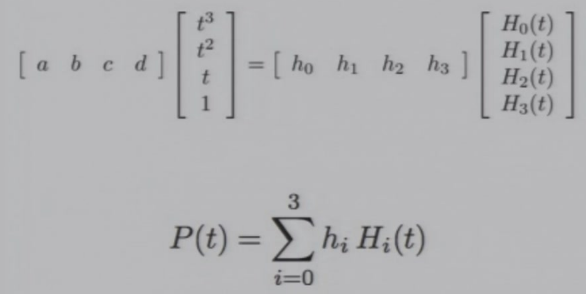

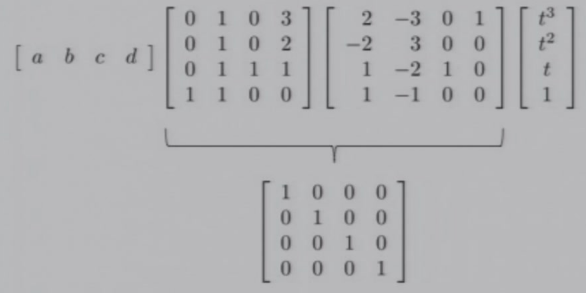

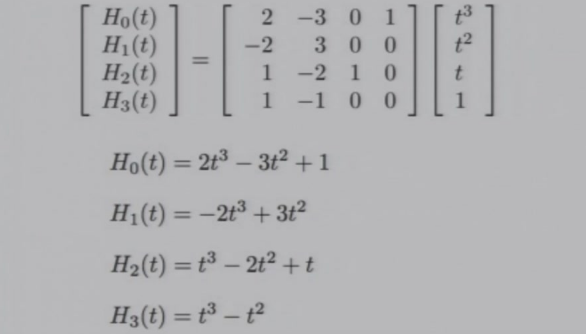
本质上是从以\([t^3,t^2,t,1]\)为基,变成了以\([H_0(t),H_1(t),H_2(t),H_3(t)]\)为基
Hermite Basic Function
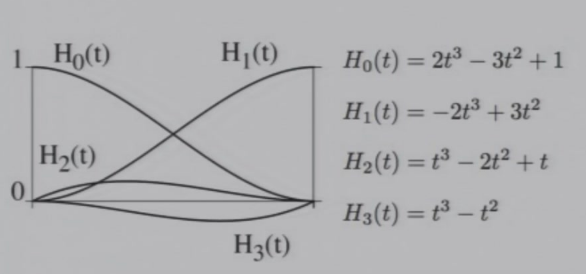
\(H_1(t)\)函数可以用作动画,开始和停止都会比较慢
多个点的插值:相邻的两个点做一次三次插值
- 由于插值保证所有点的导数不变,因此曲线一定连续
7.3.3 Catmull-Rom 插值
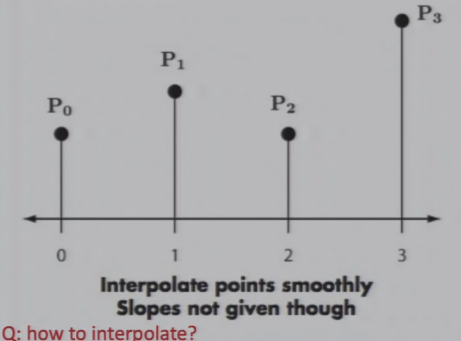
找每个点的斜率:
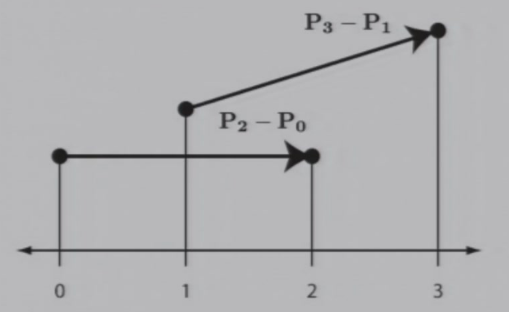
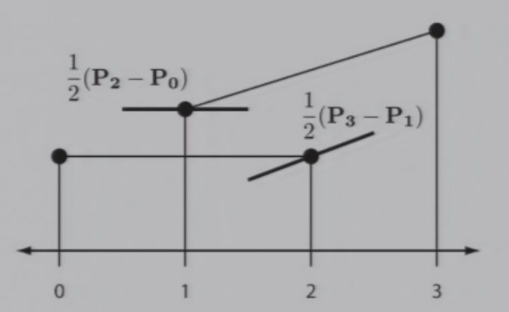
要找两个邻居,而不是找一个邻居:
- 一个邻居的偏差为\(O(n)\),两个邻居的偏差为\(O(n^2)\)
- 通过泰勒展开证明

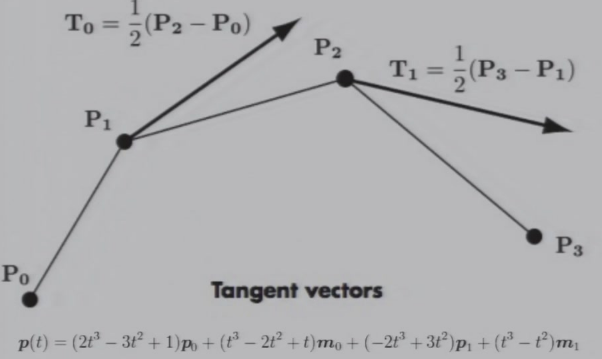
7.4 Bezier Curve 贝塞尔曲线
7.4.1 计算方式
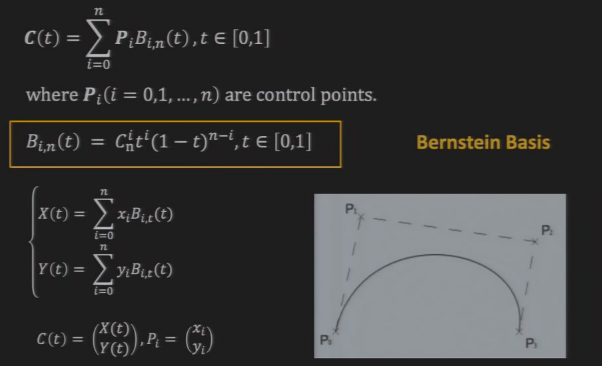
7.4.2 性质
每个点的权重\(\ge 0\)
所有点的权重和为\(1\)
权重有对称性
穿过第一个点、最后一个点
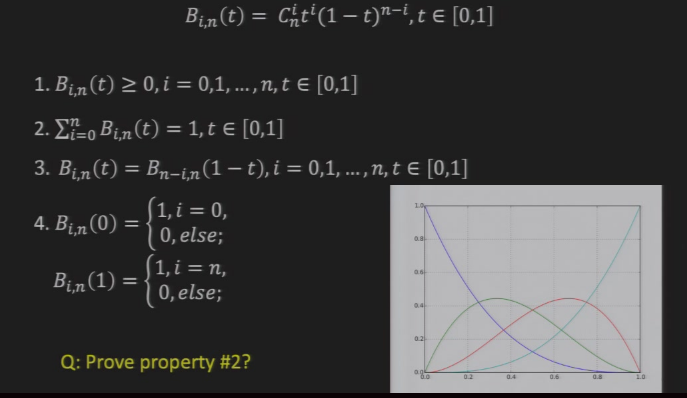
\(P_0P_1,P_{n-1}P_n\)为\(P_0,P_n\)处的曲率

仿射不变性:先变换后采样的结果 == 先采样后变换的结果

贝塞尔曲线一定在所有控制点的凸包内
贝塞尔曲线一定不会比直接连线更陡

7.4.3 示例


7.4.4 OpenGL中的贝塞尔曲线


7.4.5 Rational Bezier Curve 有理贝塞尔曲线
- 每一个点对最后曲线的权重可以调节
- \(P_i\)的权重设为\(w_i\)


7.4.6 贝塞尔曲线的缺点
- 控制点个数对应表达式的阶数,点过多时阶数过大
- 每一个控制点对全局均有影响
7.5 B-spline
- 阶数与控制点个数无关
- 局部控制
- 本质上是成片的相接的多项式

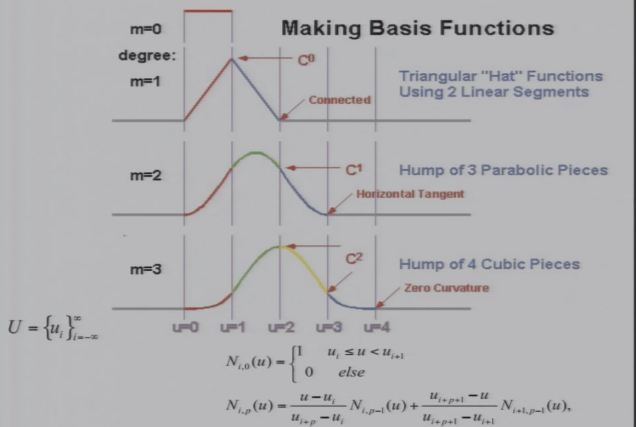
7.5.1 NURBS
Non-Uniform Rational B-Spline:区间段的长度可以由人工控制

7.5.2 OpenGL中的NURBS

7.6 总结
- 从顶点上来看:曲线本质上是对控制点的加权平均,权重由basis function决定
- 从函数上来看:曲线是由不同的函数线性组合而来,权重由控制点决定,basis function固定不变。相当于将\(P(t)\)投影到了\(B_0(t),...,B_n(t)\)的坐标轴上
Chapter 8 Surface
8.1 参数化曲线
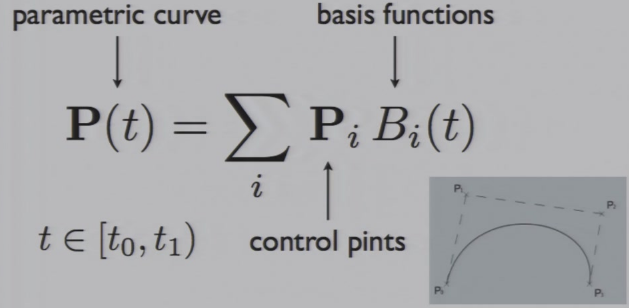
8.2 参数化曲面
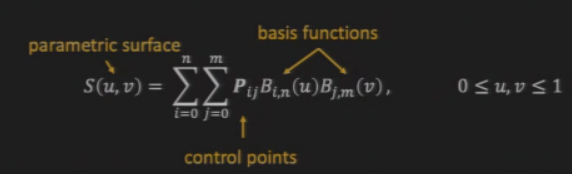
8.2.1 n阶贝塞尔曲面
8.2.1.1 曲面的表达式

8.2.1.2 贝塞尔曲线与贝塞尔曲面的联系
- \(B_{j,m}(v)\)为参数的贝塞尔曲线,计算当\(t=v\)时对应的点,共\(n+1\)个
- 作为控制点,再次计算以\(B_{i,n}(u)\)为参数的贝塞尔曲线
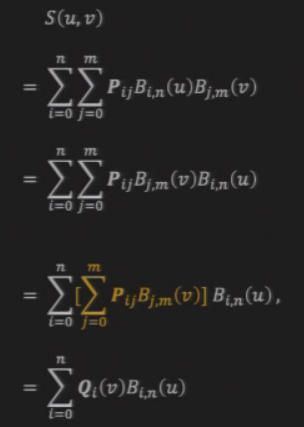
8.2.1.3 贝塞尔曲面的法向量
- 计算对于\(u,v\)的偏导,然后进行叉积
- \(N(u,v)=\frac{\partial S(u,v)}{\partial u} × \frac{\partial S(u,v)}{\partial v}\)

8.2.1.4 OpenGL中的使用

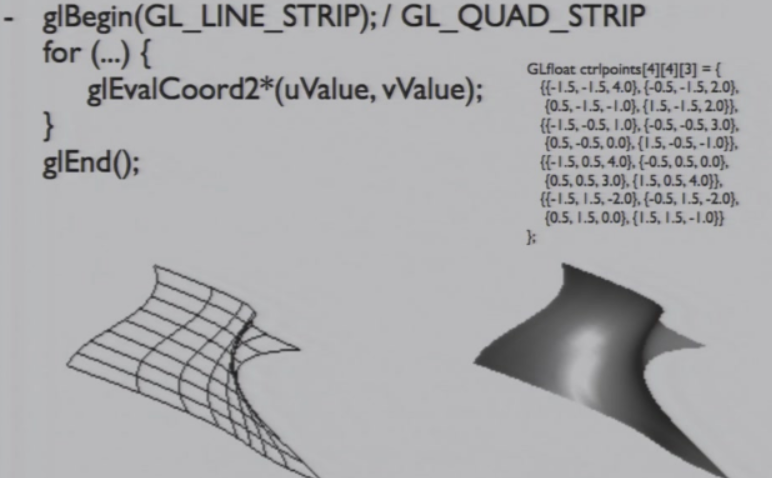
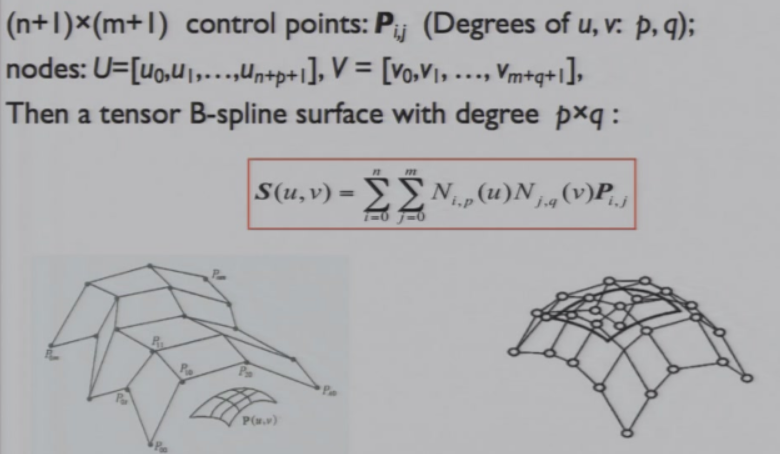
8.2.2 B-spline曲面
8.2.3 NURBS曲面
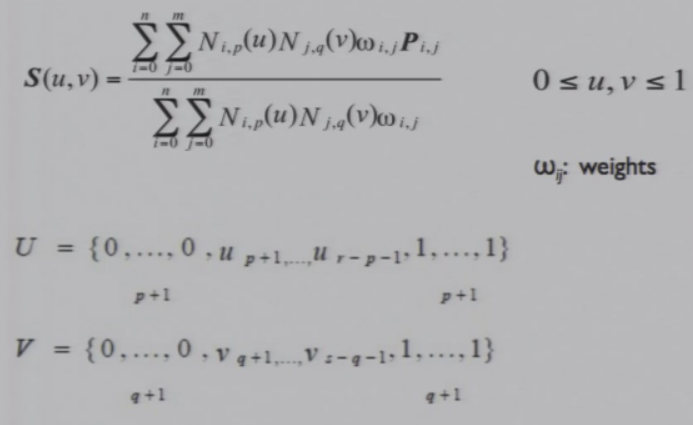
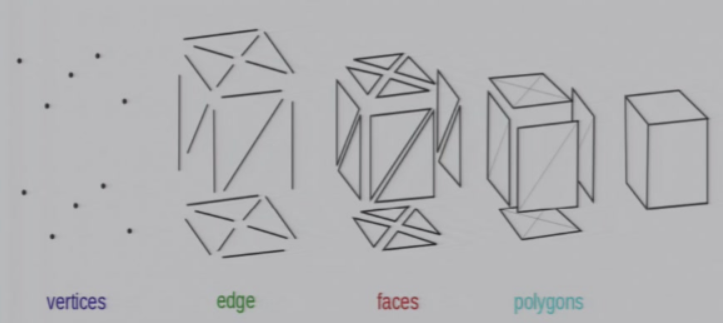
8.3 多边形网格
8.3.1 什么是多边形网格
- 在三维计算机图形学和实体建模中,定义一个多面体物体形状的顶点、边和面的集合
- 可以用许多平面近似地表示一个曲线形状
- 在游戏中呈现几何体的实际标准
8.3.2 多边形网格的表示
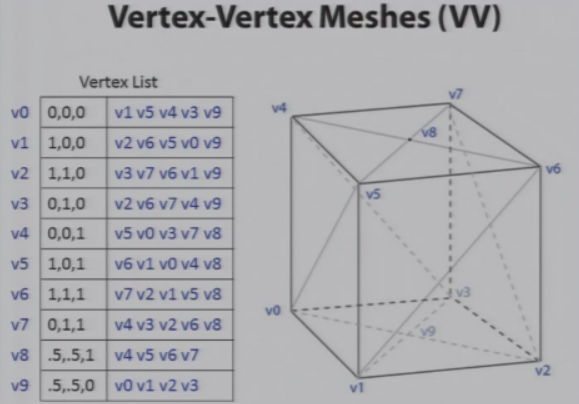
顶点信息 + 拓扑信息
Vertex-Vertex Meshes(VV)
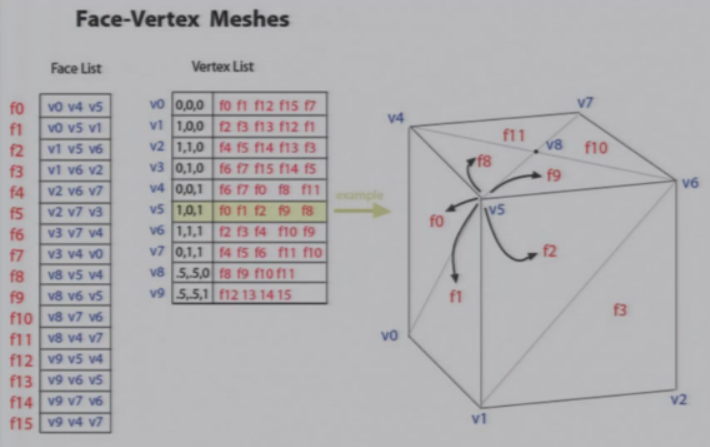
Face-Vertex Meshes
8.3.3 obj格式
8.3.3.1 示例

8.3.3.2 含义
- mtllib:导入.mtl文件
- usemtl:从该句开始后面的面,使用该.mtl文件

8.3.3.3 Wavefront .obj file
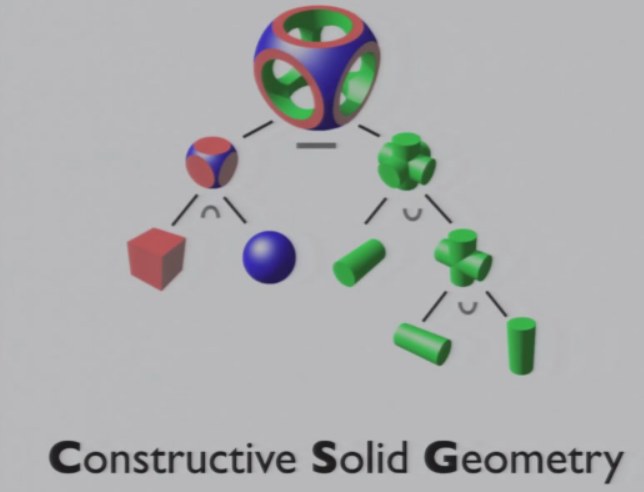
8.3.4 Constructive Solid Geometry 构造实体几何
8.3.5 L-system:Formal grammar
Formal grammar
- Alphabet:字母表
- Production rules:推导规则
- An initial axiom:公理
最后的字符串对应一个图像
应用
- 植物
- 分形
示例:
生成字符串
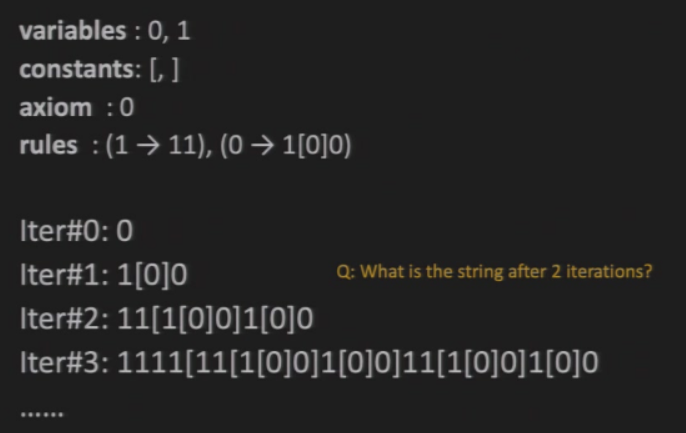
解释这个字符串
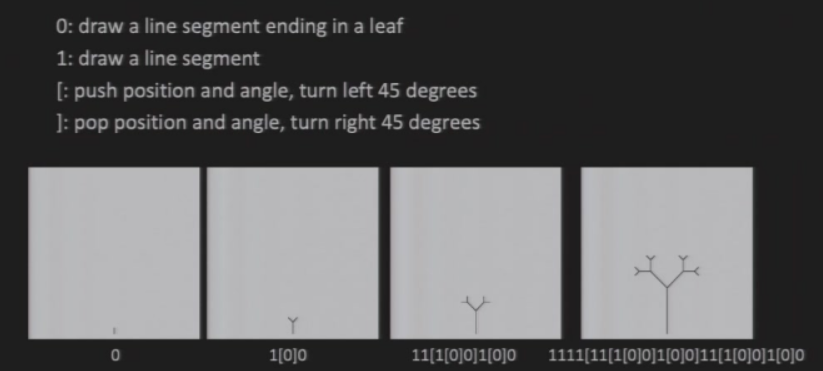
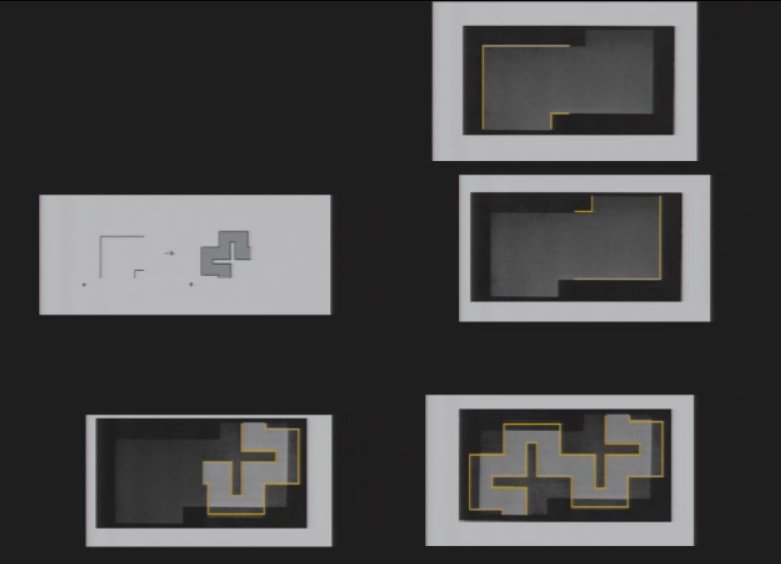
8.3.6 Shape Grammar
将推导规则定义在形状上

例:
8.3.7 Subdivision Curves/Surface
- 从一些顶点开始
- 根据规则,生成新顶点,替换旧顶点:Geometric rule
- 根据规则,将新顶点连起来:Topological rule
- 重复若干次,直到收敛
8.3.8 使用生成方法的优点
- 可以构造复杂图形
- 容易生成
- 容易通过控制初始点,控制网格
- LOD
- 可以由GPU通过geometry shader原生支持
8.4 Sweeping
由一个图形+轨迹生成网格

8.5 总结

问题:观察者如何看到光源? 回答:反射光源必须经过人眼,即人眼与反射点的连线与法向量n的夹角,与i与n的夹角相同,且三者共面
Chapter 9:Digital Material Appearance
9.1 Introduction
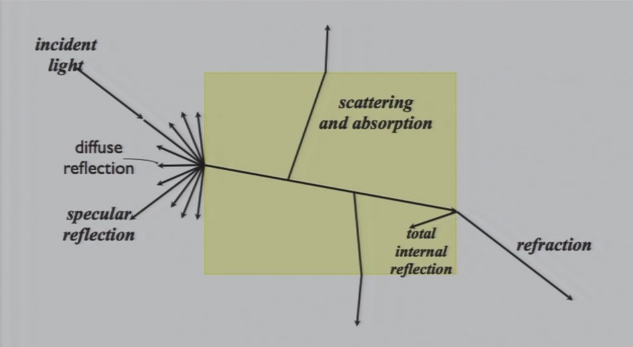
光与物体的交互:
- 吸收
- 反射:颜色、光泽
- 穿透
9.2 Reflection Models
9.2.1 BRDF
Bidirectional Reflectance Distribution Function f(i,o)
- i:入射方向
- o:出射方向
- 是一个4D函数:因为是单位向量,消去了一个自由度
- 一个单位球上确定一个向量,只需要2个自由度(经度、纬度)
- 固定i,一个出方向的二维函数描述了入射光如何沿不同方向反射
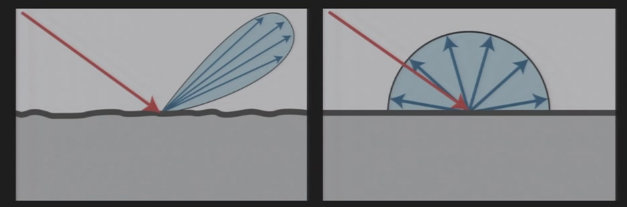
9.2.2 完美镜面反射
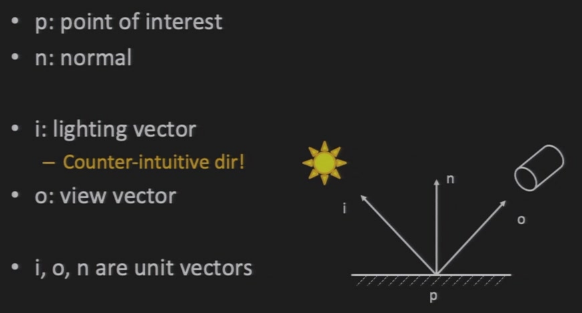
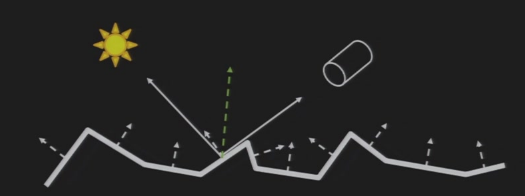
- 观察者如何看到光源:\(\vec{o}\)与\(\vec{i}\)关于法向量\(\vec{n}\)的夹角相等,且三者共面
- 判断夹角是否相等:\(\vec{h}=\frac{\vec{i}+\vec{o}}{||\vec{i}+\vec{o}||}\)与\(\vec{n}\)的方向相同
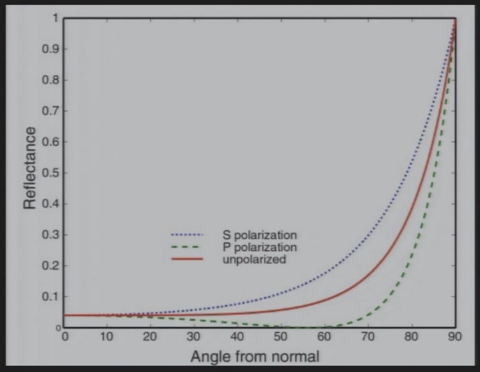
9.2.3 Fresnel Reflectance Term
| 绝缘体 | 导体 |
|---|---|
 |
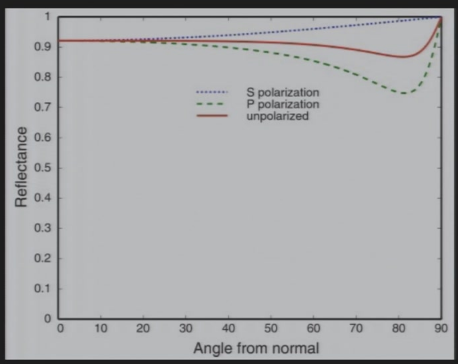 |
计算镜面反射率:\(n_1,n_2\)为两者的反射率,\(\theta\)为\(\vec{i}\)和\(\vec{n}\)的夹角 \[ R(\theta)=R_0+(1-R_0)(1-cos\theta)^5 \\ R_0=(\frac{n_1-n_2}{n_1+n_2})^2 \]
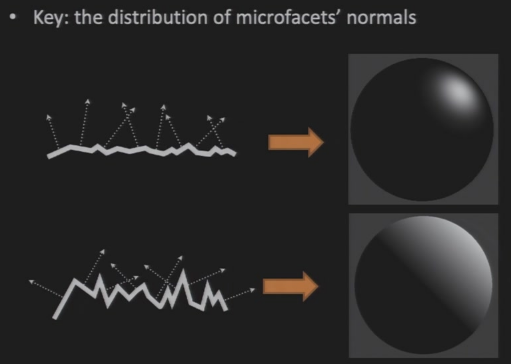
9.2.4 Microfacet-Based Models
- 当平面非常小时,均为镜面反射
- 微面的反射只与微面的方向有关系
Microfacet-Based Models的计算公式
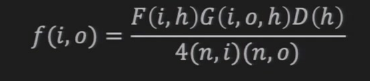
\(D(h)\):有百分之多少的微面,法向量=\(\vec{h}\)
- 如果微面的法向量≠\(\vec{h}\),则在当前的\(\vec{i},\vec{o}\)的情况下,不可能发生镜面反射,如下图所示
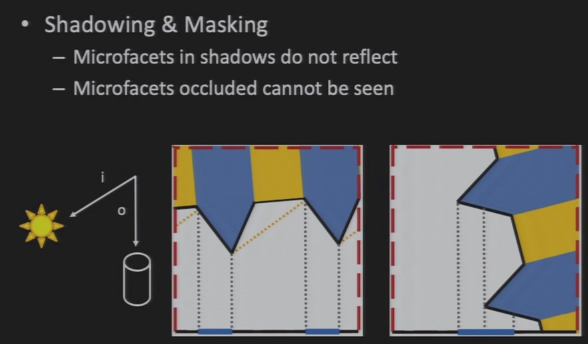
\(G(i,o,h)\):计算遮挡的情况
- 微面的法向量=\(\vec{h}\),可能发生镜面反射,但由于阴影/遮罩,也可能无法发生镜面反射
\(F(i,h)\):镜面反射率
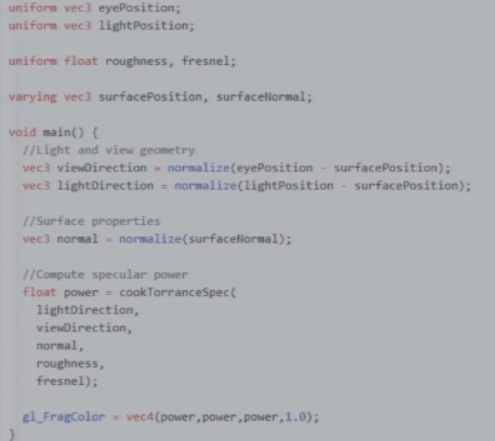
Microfacet-Based Models的一个具体的计算方式:Cook-Torrance Model

9.2.5 Anisotropic BRDF 各向异性
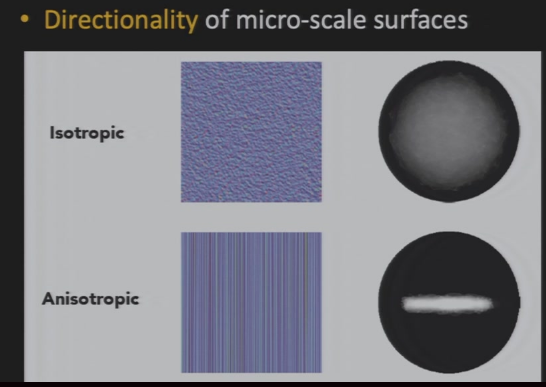
9.3 Diffuse Reflection 漫反射

- 一束光打过来,沿每一个可能的出射方向的反射率是相同的:\(f(i,o)=constant\)
- 这只是观察到的情况,物理上不是这样的
- 物理上是先吸收,后反射
9.4 两种反射结合

- 金属的高光颜色为表面颜色,塑料的高光颜色为白色
- 额外的一个cos(i, n)表示光实际打到表面的能量占比
9.5 BRDF模型在GLSL中的实现

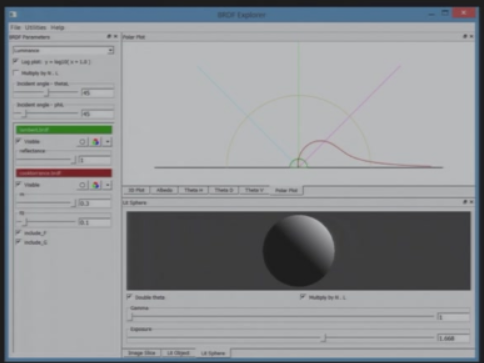
9.6 实用工具
https://www.disneyanimation.com/technology/brdf.html
9.7 Reflectance Capture
9.7.1 直接采样

9.7.2 光照多路复用

灯光舞台
- 同时使用数百个光源
- 只有一个或几个摄像头
- 投射特定的模式并使用查找表恢复反射率
- 效率更高
- 广泛用于电影制作

9.8 总结


Chapter 10:Texture
10.1 什么是Texture Mapping
- Surface存在在3D世界空间中
- 每个3D表面点在2D图像和2D纹理中也有一个位置
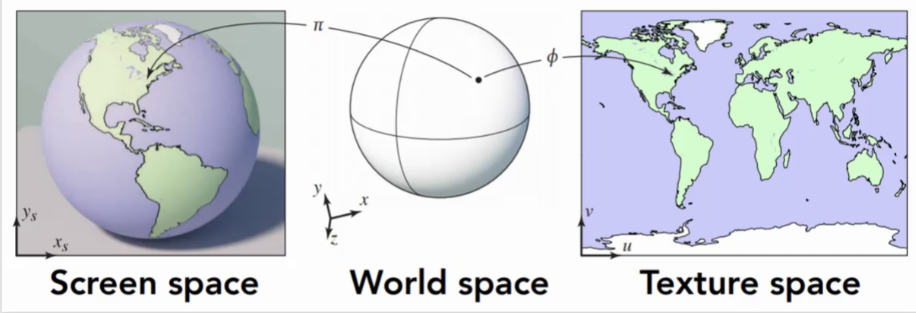
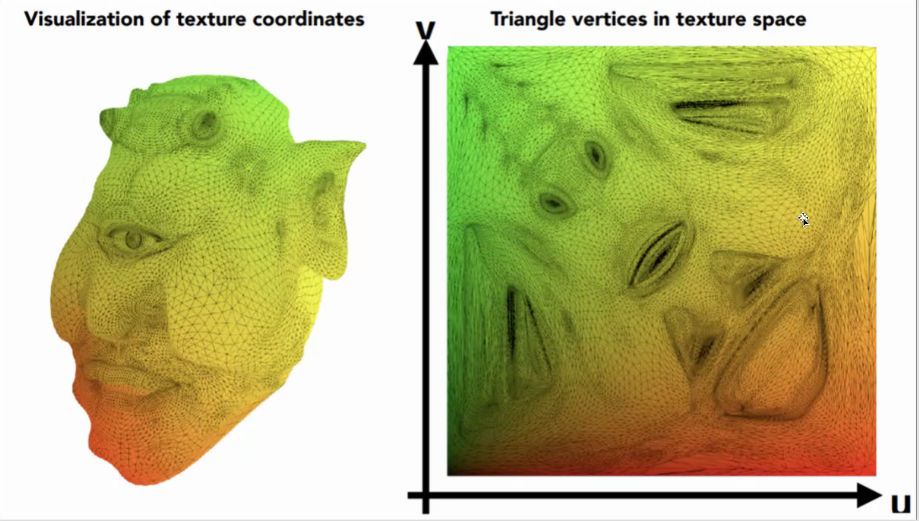
10.2 Texture Coordinates
- 纹理坐标也叫UV坐标
- UV坐标系左下角为(0,0),右上角为(1,1)
10.3 Sponza Palace Model
- 一个小的纹理贴图,可以通过重复,将其映射到一个大的物体上


10.4 如何生成纹理坐标
10.4.1 参数化曲面

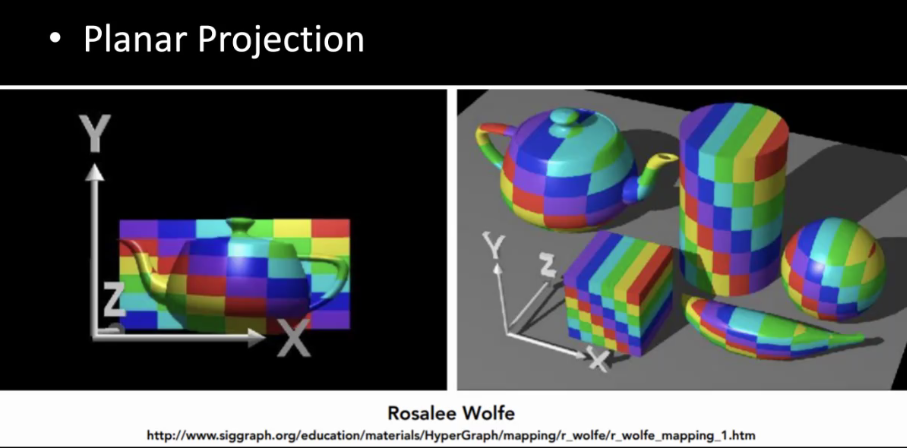
10.4.2 平面投影
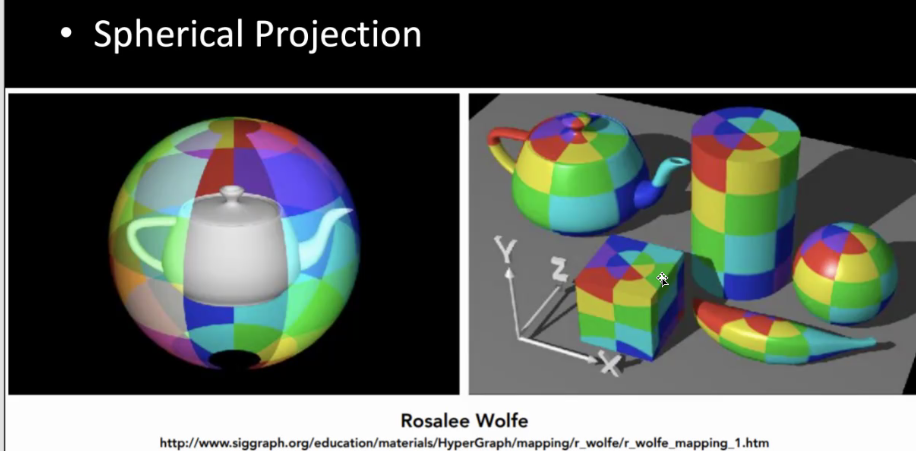
10.4.3 球面投影
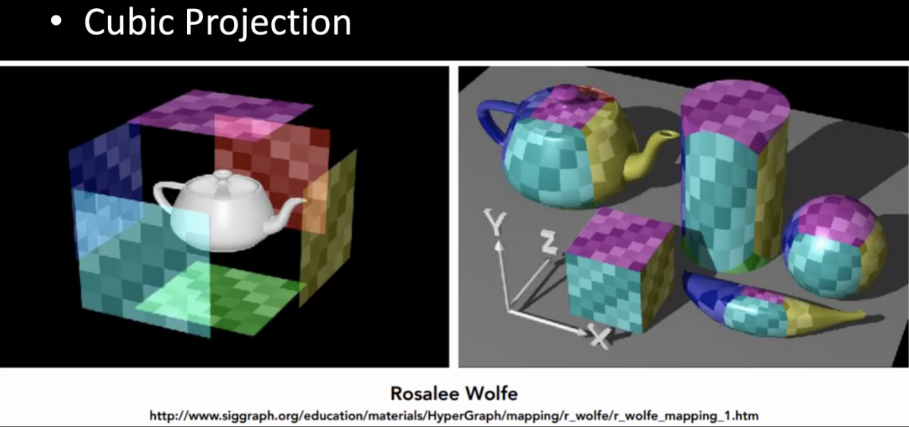
10.4.4 立方体投影
10.4.5 复杂表面
- 将物体分为不同的部分,分别使用不同的投影方法
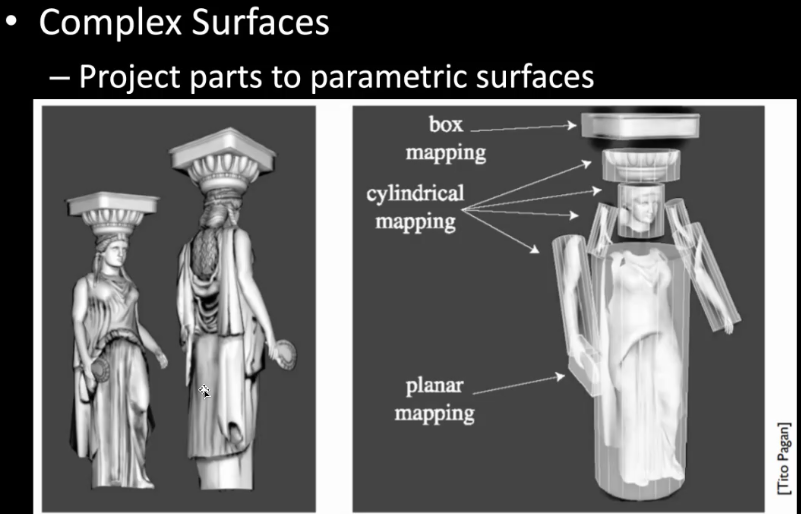
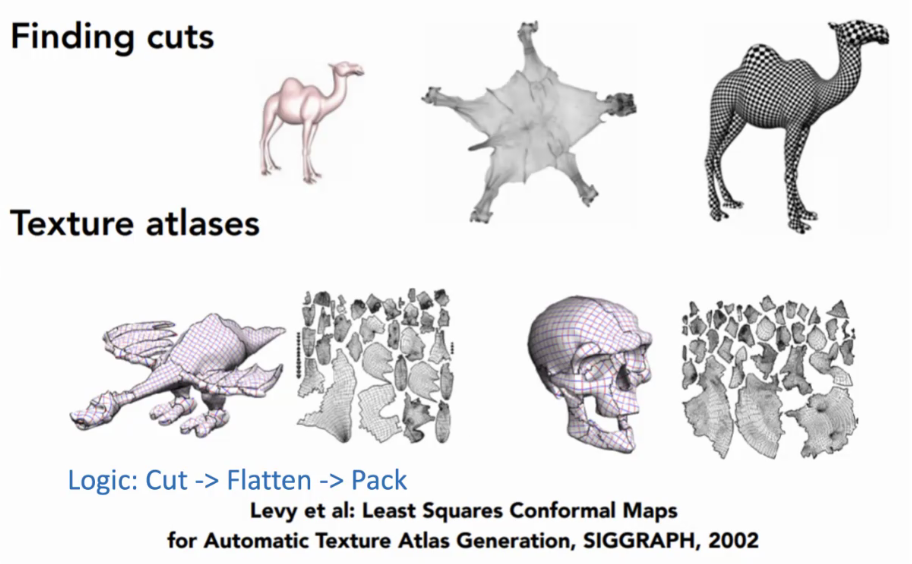
10.4.6 实际上的操作
- 切分 cut
- 摊平 flatten
- 打包 pack
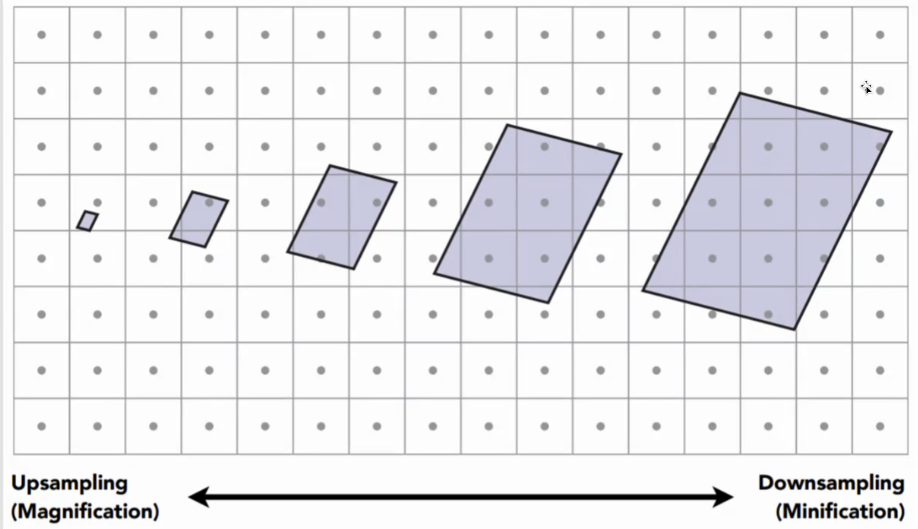
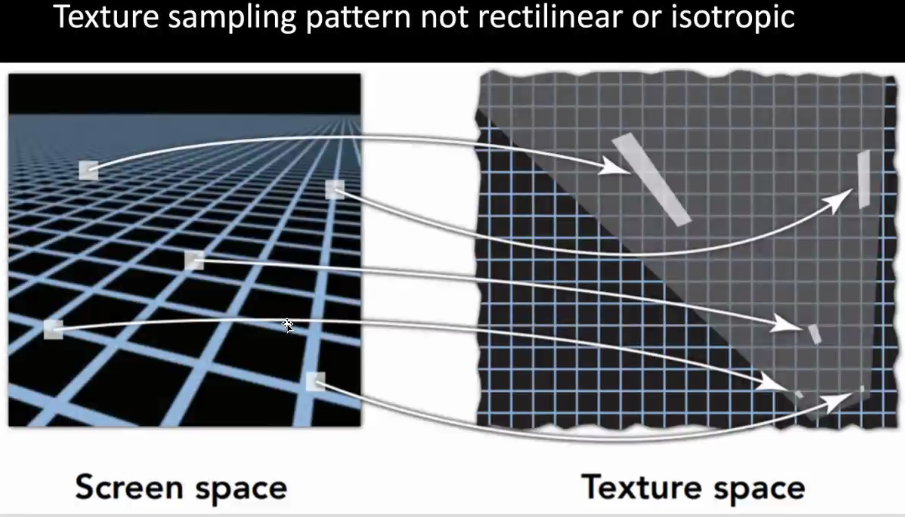
10.5 Texture Mapping实质是重采样

10.6 屏幕坐标 vs 纹理坐标
在最佳观看尺寸下
- 一个像素样本 <==> 一个纹理样本
- 取决于纹理分辨率,例如512x512
当放大时(离我们越近):
- 多个像素样本 <==> 一个纹理样本
当缩小时(离我们越远):
- 一个像素样本 <==> 多个纹理样本
计算具体的对应关系:
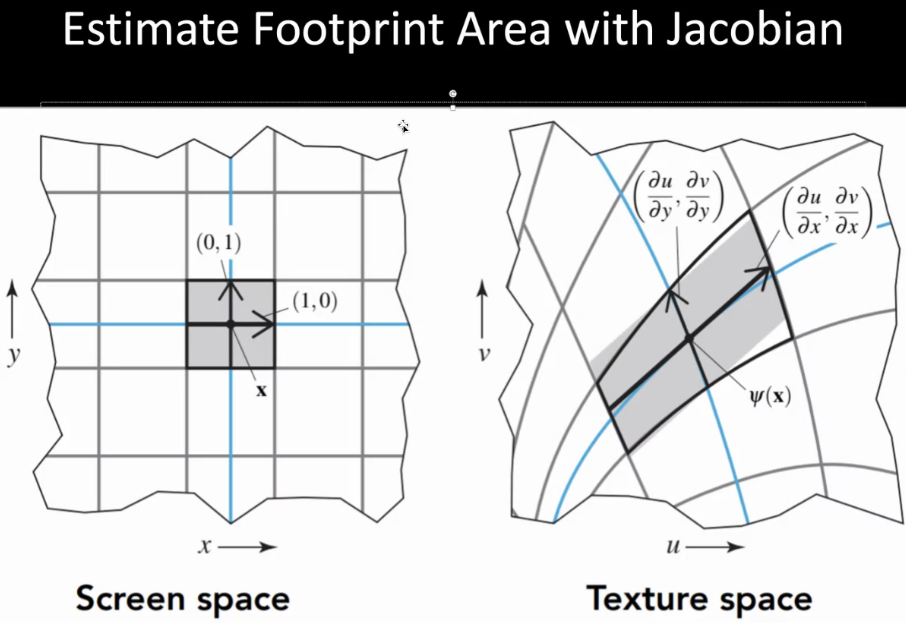
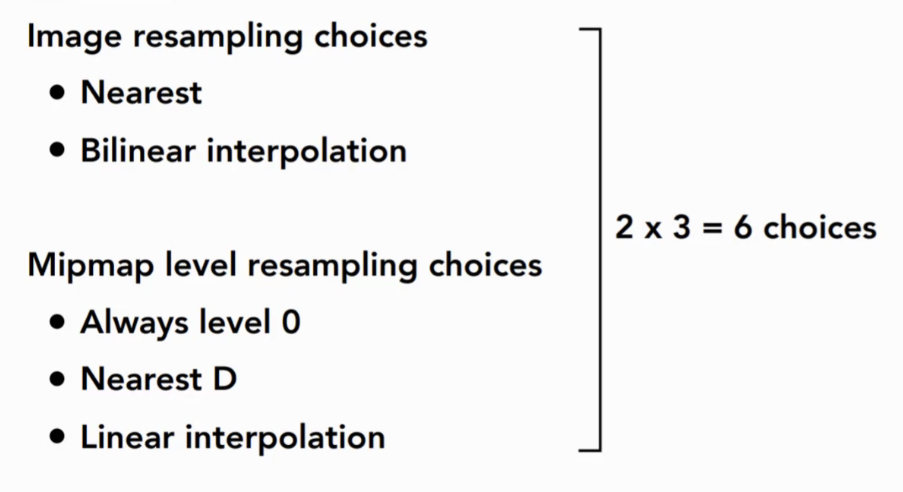
10.7 Texture Filtering
- 采样率不匹配可能导致混叠效应
- Idea:去掉超出采样率的“坏”高频部分
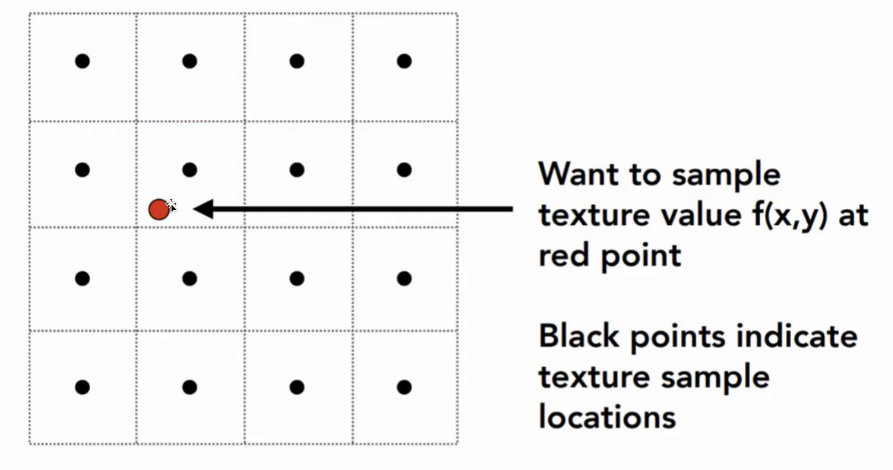
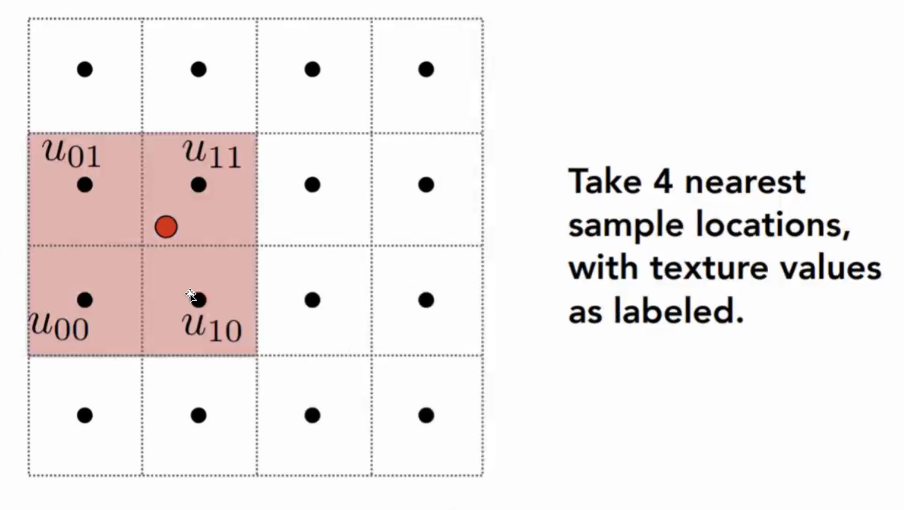
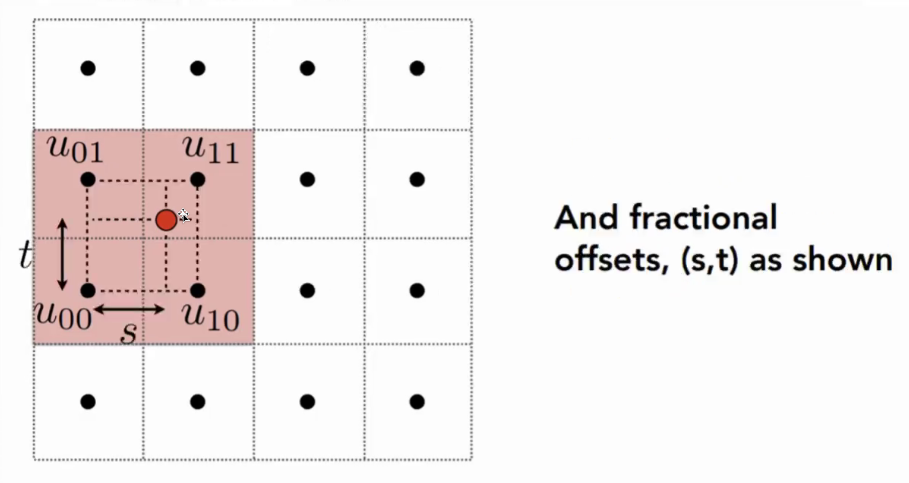
10.7.1 纹理放大:Bilinear Filtering 双线性滤波

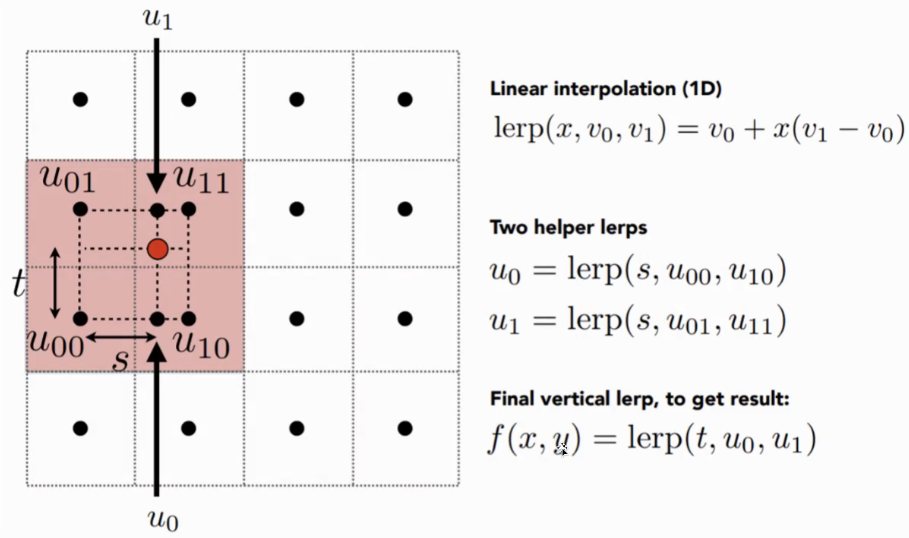
- 想要计算红点的值
- 找4个临近的节点,进行两次线性插值
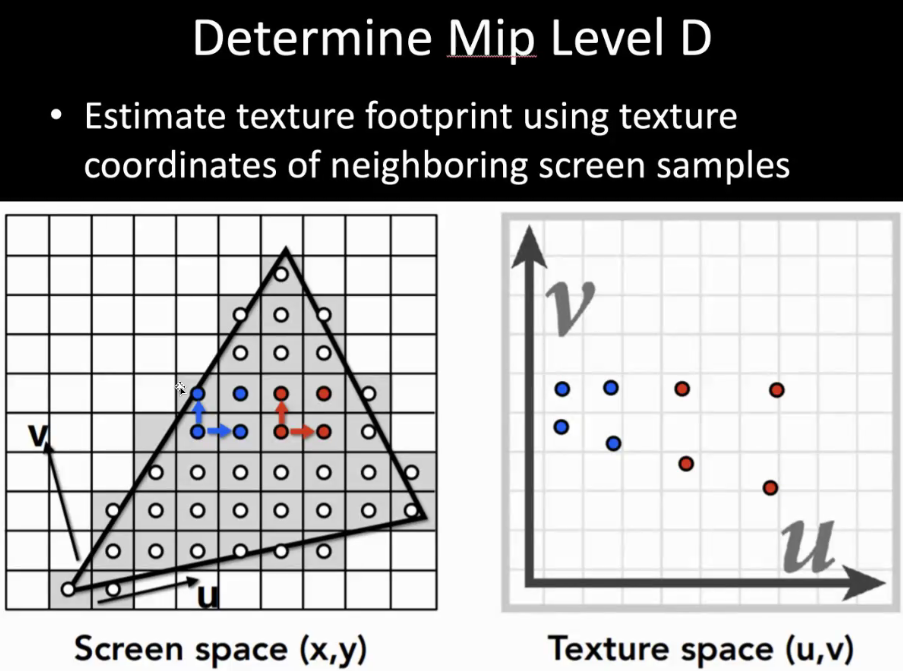
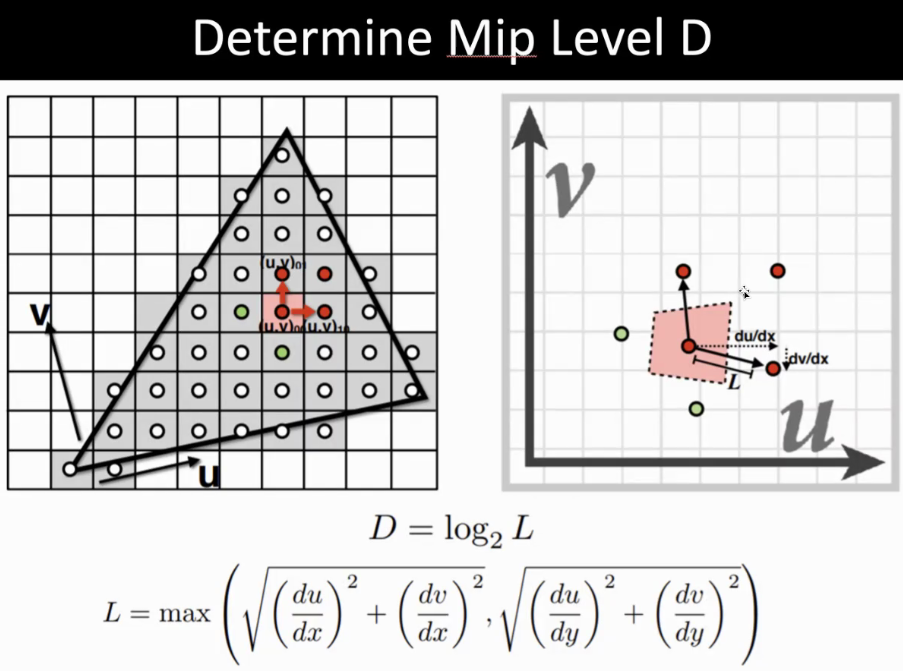
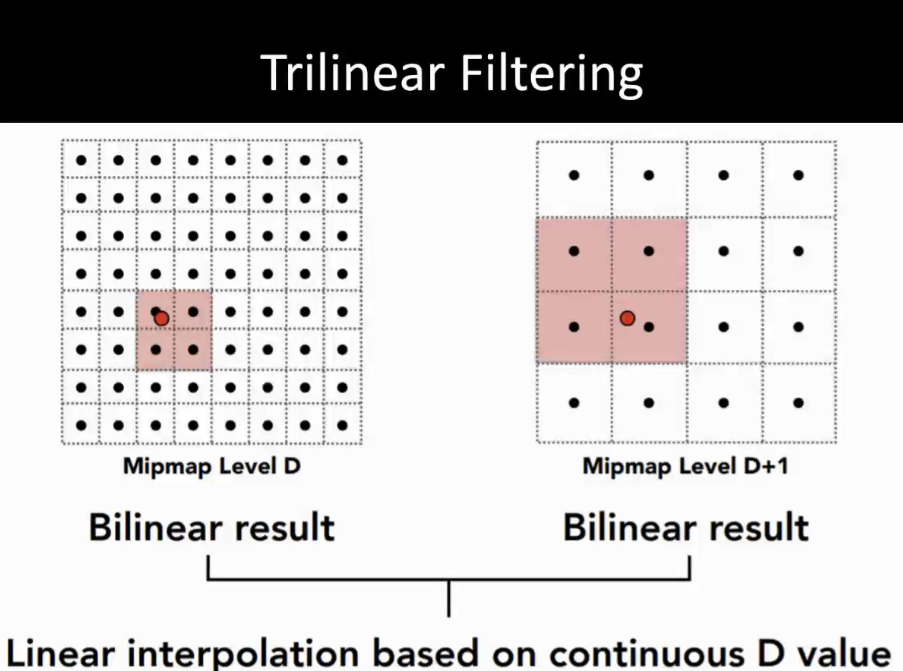
10.7.2 纹理缩小:Mipmap => Trilinear Filtering
- Challenge
- 许多texels会增加像素占用
- pixel footprint的形状可能很复杂
- Idea
- 低通过滤器、降低采样率
- 使用与屏幕采样率匹配的分辨率
Mipmap:将
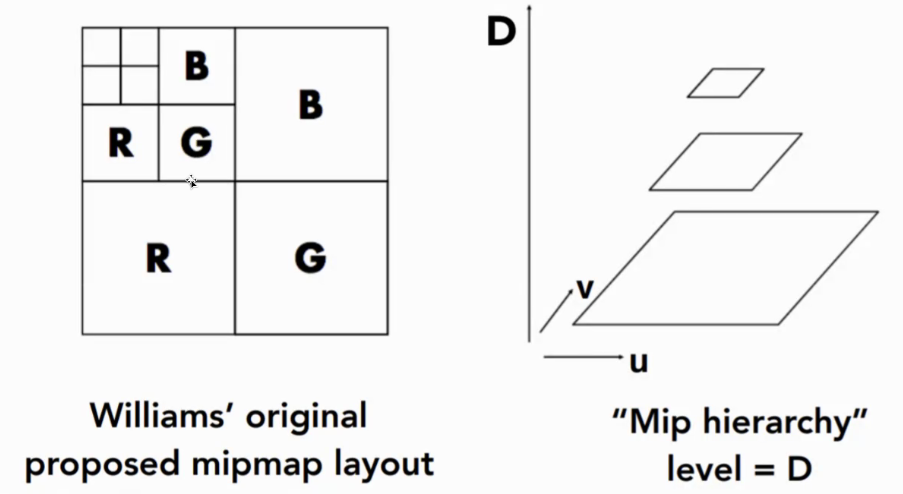

Trilinear Filtering
- 在每个Mipmap Level中进行一次Bilinear
- 在Mipmap Level之间进行一次线性插值

OpenGL中的设置:
Mipmap的局限:
- 远处的地方,应该是对应一个椭圆,但mip level认为是一个圆形


10.8 高级纹理映射
纹理 = 内存 + 滤波
- 为分段计算提供数据的一般方法
应用程序
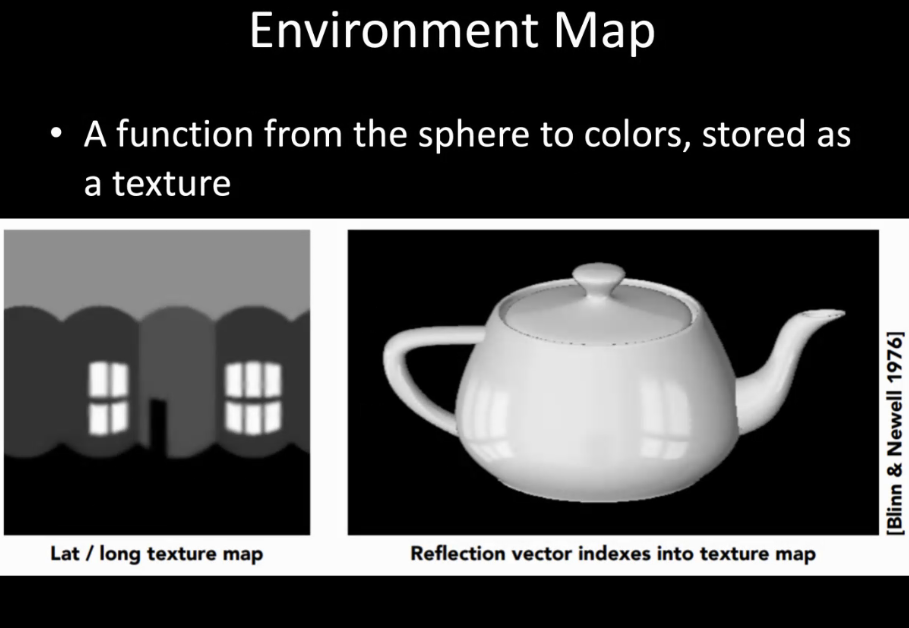
环境照明
Micro-geometry映射
程序上的纹理
双向体绘制




结构函数
10.9 总结

Chapter 12:Advanced Real-time Rendering
12.1 阴影贴图
阴影对真实感非常重要
- 可以显示物体之间的位置关系
- 光源的位置
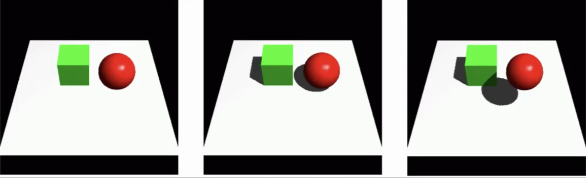
如何判断点是否在阴影里面:点在灯的视角中被物体遮挡了(深度测试)
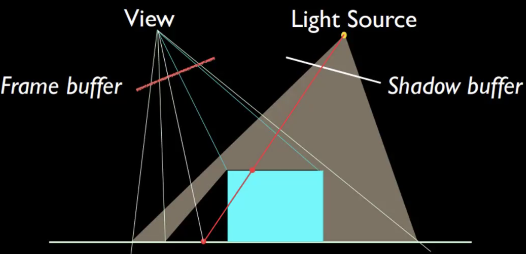
单个点光源的阴影计算:
- 将光源作为眼睛,只渲染深度,相关的深度缓冲存储为阴影贴图
- 对每一个被渲染的点,将其更改到光源的视角,用阴影贴图中的z-value进行测试
- 如果不包含,则不使用阴影渲染
- 否则,渲染阴影
多个点光源的阴影计算:
- 计算每个点光源的阴影贴图,然后做线性相加
面光源的阴影计算:
- 将面光源采样为多个点光源
常见问题
在Z的判断上精度不够:添加一个offset,而不是完全判断相等

当分辨率不高时,相机与光源的采样率区别很大:Perspective Shadow Map


12.2 Precomputed Radiance Transfer
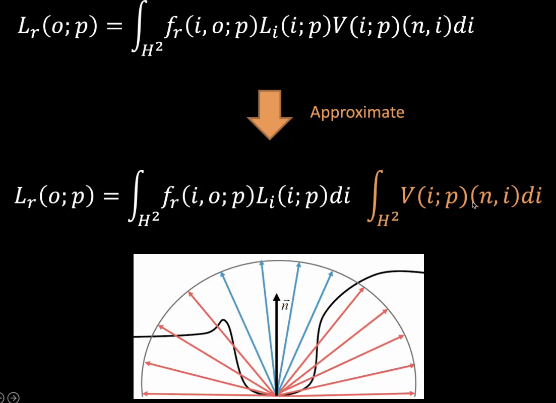
反射的公式:
- Li(i, p):入射光为i时,点p的能量
- V(i, p):入射光为i时,点p的可视性
- (n,i):一个cos<n, i>值
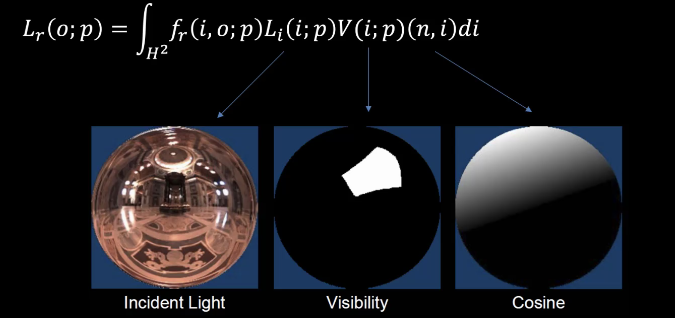

如何计算积分:随机采样
如何高效计算:预先计算好结果
预计算,假设:
光源很远:表示光Li(i)

静态场景:可见性函数V(i, p)可以提前计算
Lambertian材质:

预计算:可以将积分改变为两重循环的积分
卷积定理:
- 一个域下的卷积,是它对偶域上的点积

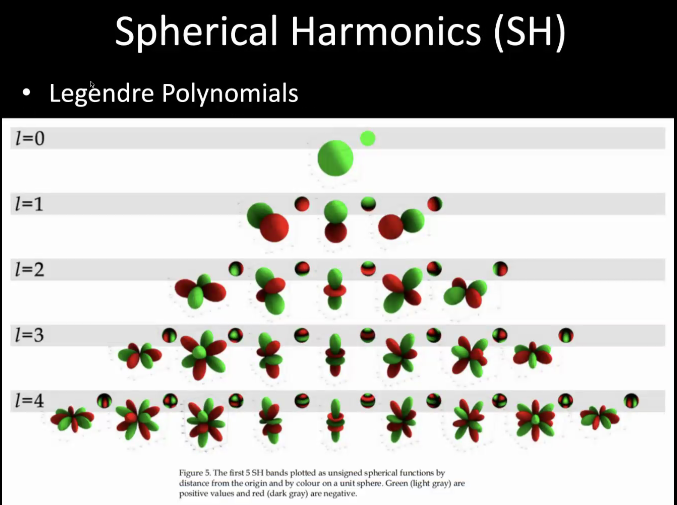
使用什么Base Function?
- Spherical Harmonics:球面谐波
- Haar Wabelets:哈尔
- Gaussian Mixtures:高斯混合
如何计算参数?
- 卷积,即F(i)和Bk(i)的卷积
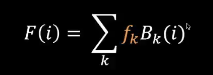
SH Lighting:通常用16个参数即可
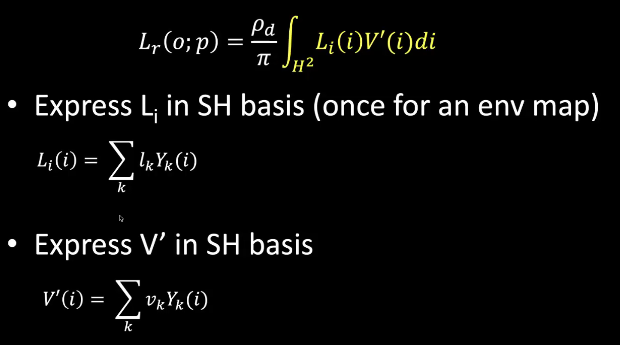


Haar Wabelet:
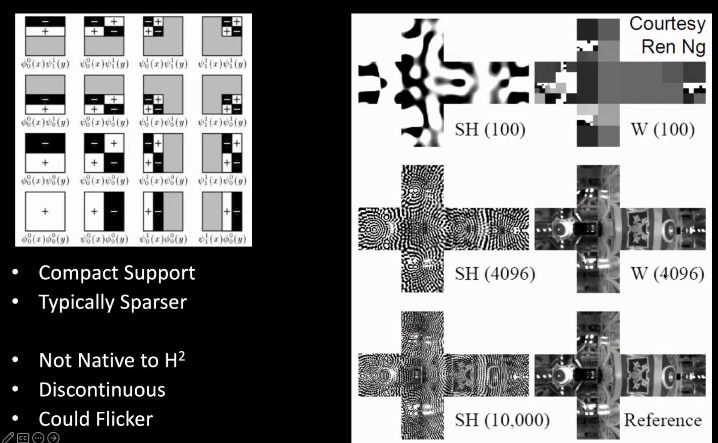
Gaussian Mixtures


12.3 Screen-Space Ambient Oocclusion(SSAO)
- 软阴影
- 是后处理,天然计算动态计算
- 利用了标准z-buffer

12.3.1 SSAO对反射公式的近似
12.3.2 为什么要用屏幕空间

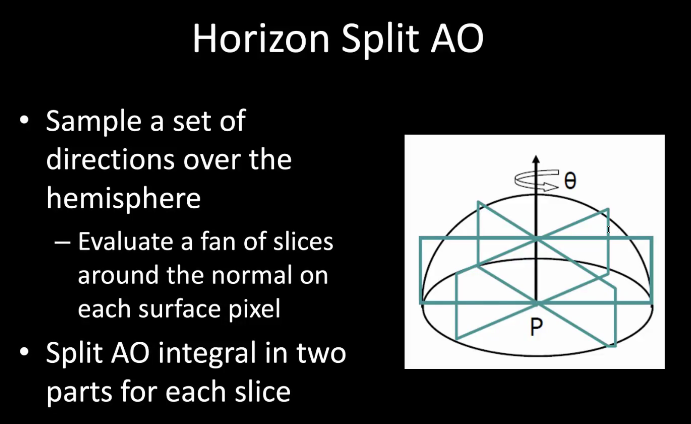
12.3.3 Horizon Split AO

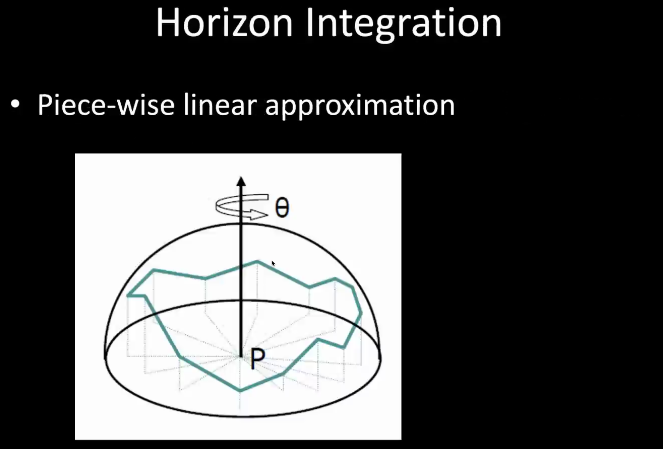
12.3.4 SSAO Demo
