GAMES101-13:光线追踪1:Whitted-Style Ray Tracing
十三、光线追踪1:Whitted-Style Ray Tracing
13.1 为什么要使用光线追踪
光栅化不能很好解决全局效果
- 软阴影
- Glossy反射
- 间接光照

光栅化的速度很快,但是质量较低,通常用于实时渲染
光线追踪质量高,但是非常慢,通常用于离线制作
13.2 基础光线追踪算法
13.2.1 光线是什么
- 光线沿直线传播
- 光线和光线不会发生碰撞
- 光线从光源发出,经过反射、折射等过程,进入人的眼睛:光路可逆性
13.2.2 光线投射
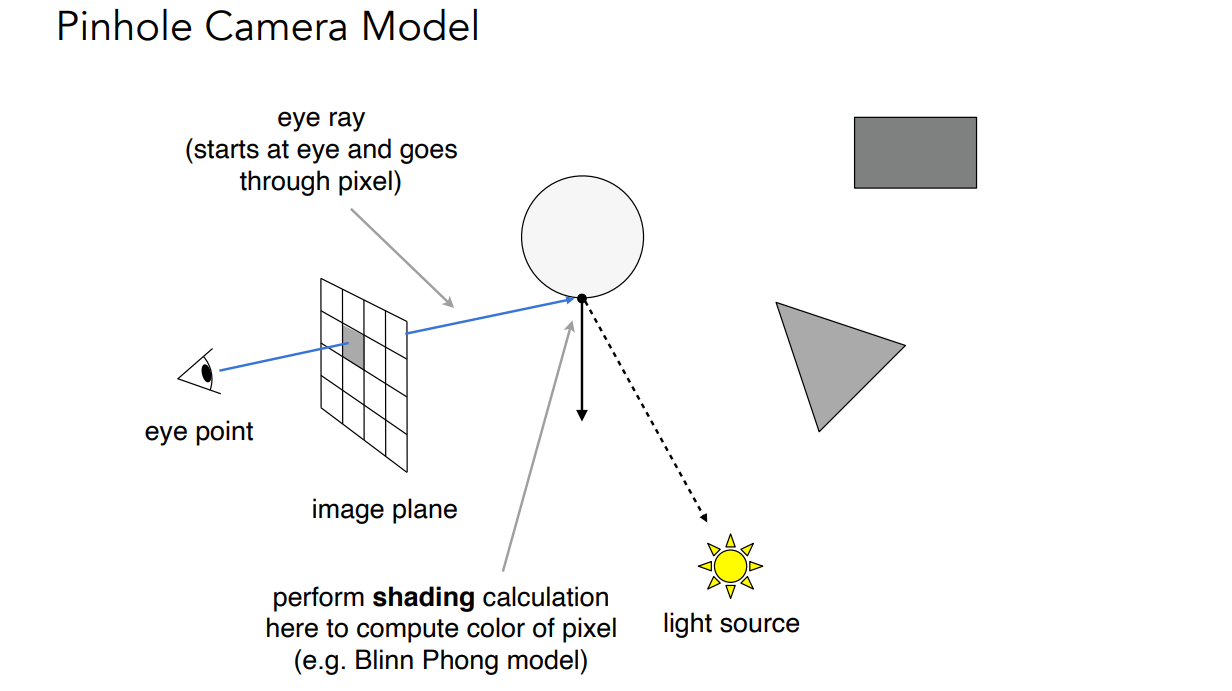
- eye ray:从眼睛到屏幕上的像素,连接的而成的射线,只记录最近的交点
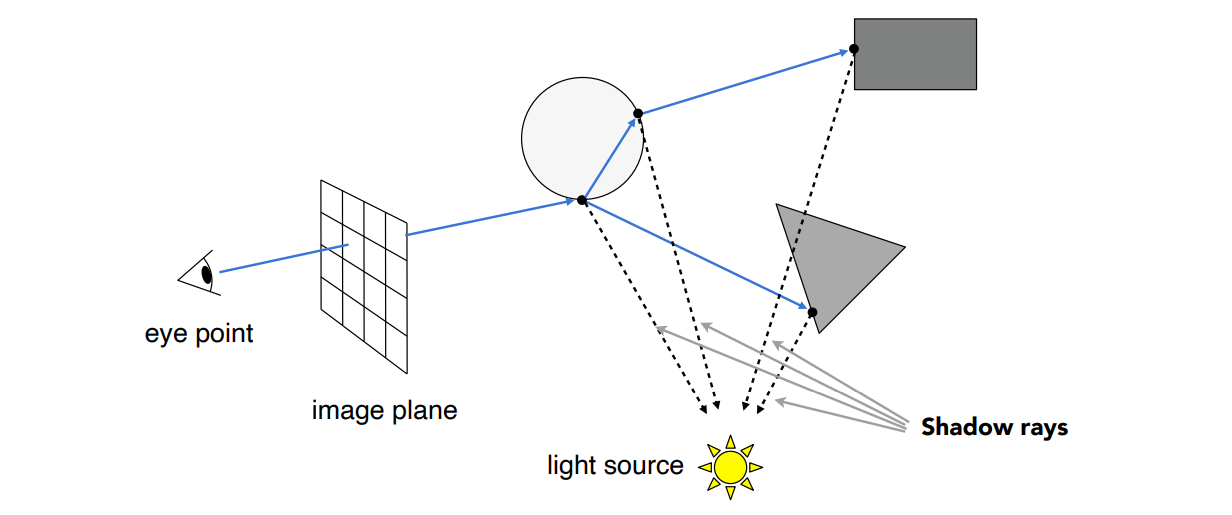
- shadow ray:从某个点到光源的连线
- 根据两条线的关系,判断着色
13.2.3 递归光线追踪
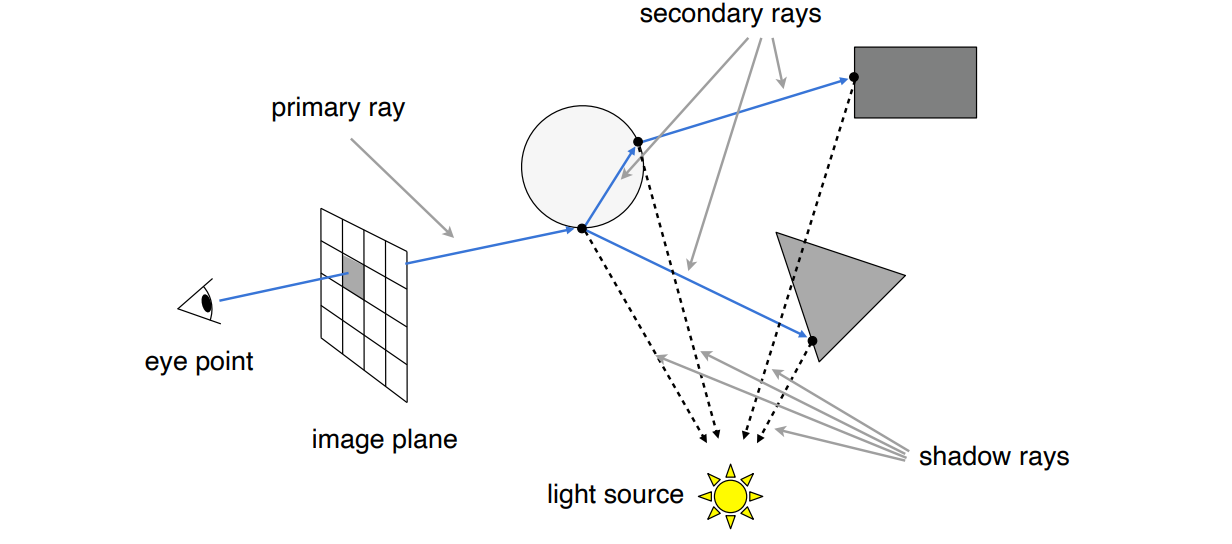
- primary ray:即eye ray
- secondary ray:经过折射/反射后的光线
13.3 光线和表面的交点
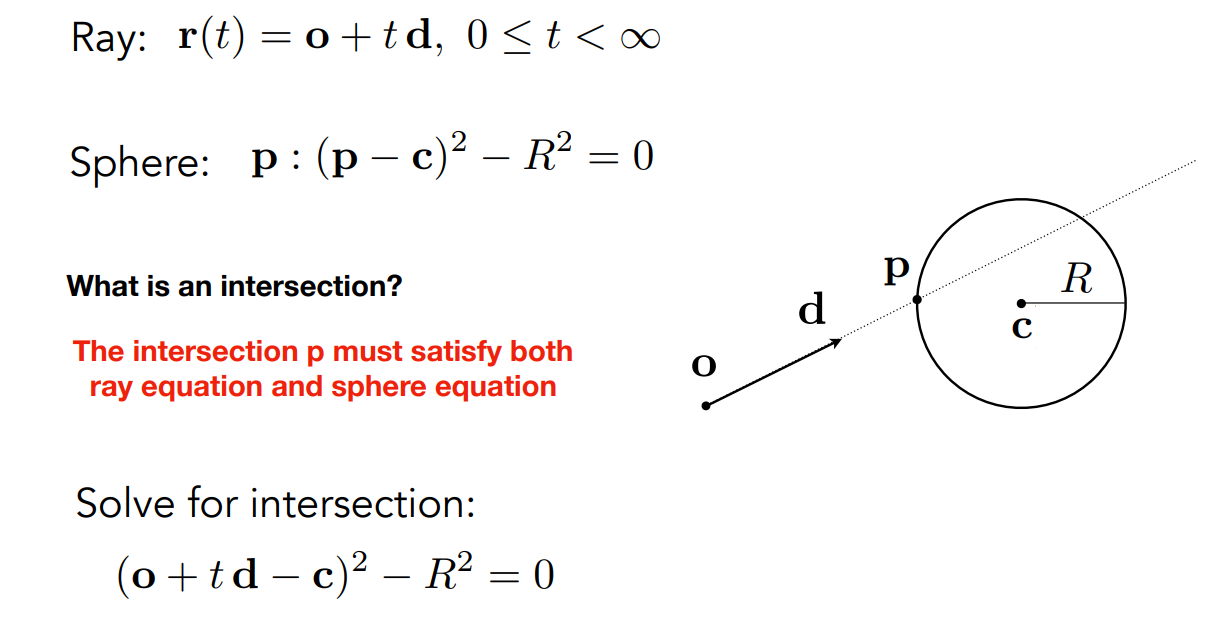
13.3.1 光线的数学定义
- 起点
o,方向d - 射线定义:
r(t) = o + td

13.3.2 光线 与 球 求交点
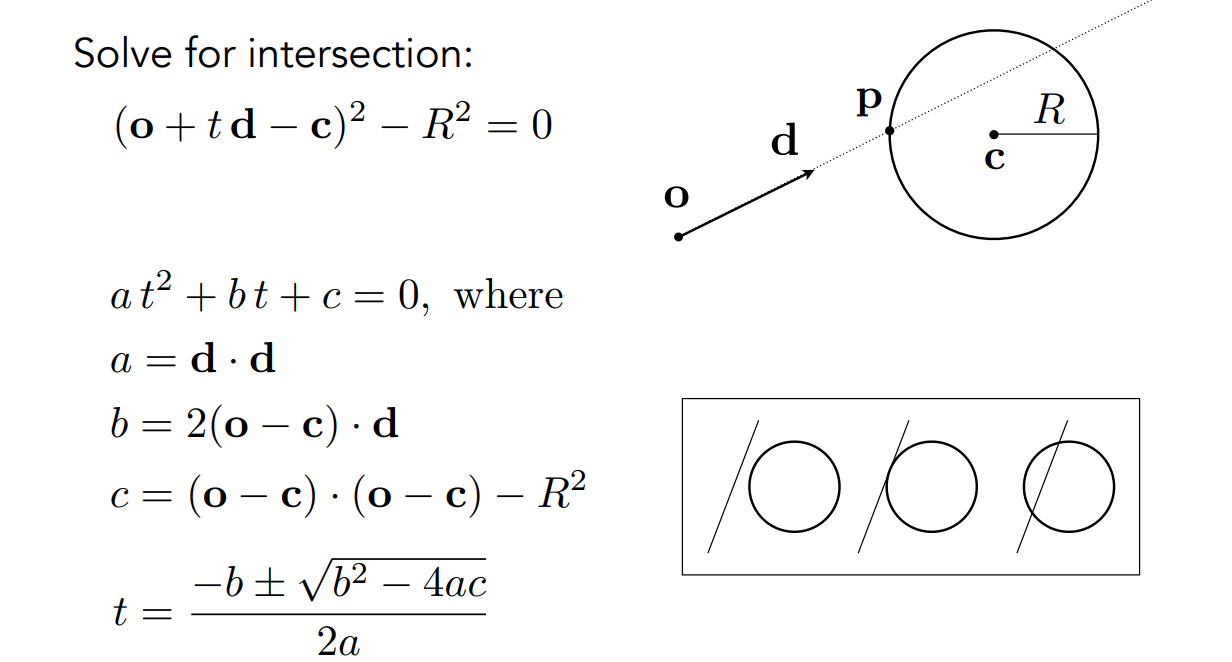
13.3.3 光线 与 隐式表面 求交点

13.3.4 光线 与 三角形 求交点
如果射线与物体的交点数量为奇数,则点在物体内;如果是偶数,则在物体外
- 光线和平面求交
- 判断点是否在三角形内
13.3.4.1 平面的数学定义
- 给一个点\(p_0\),一条法线\(\vec{N}\)
- 则平面为:\((p-p_0)·\vec{N} = 0\)

13.3.4.2 光线和平面的交点
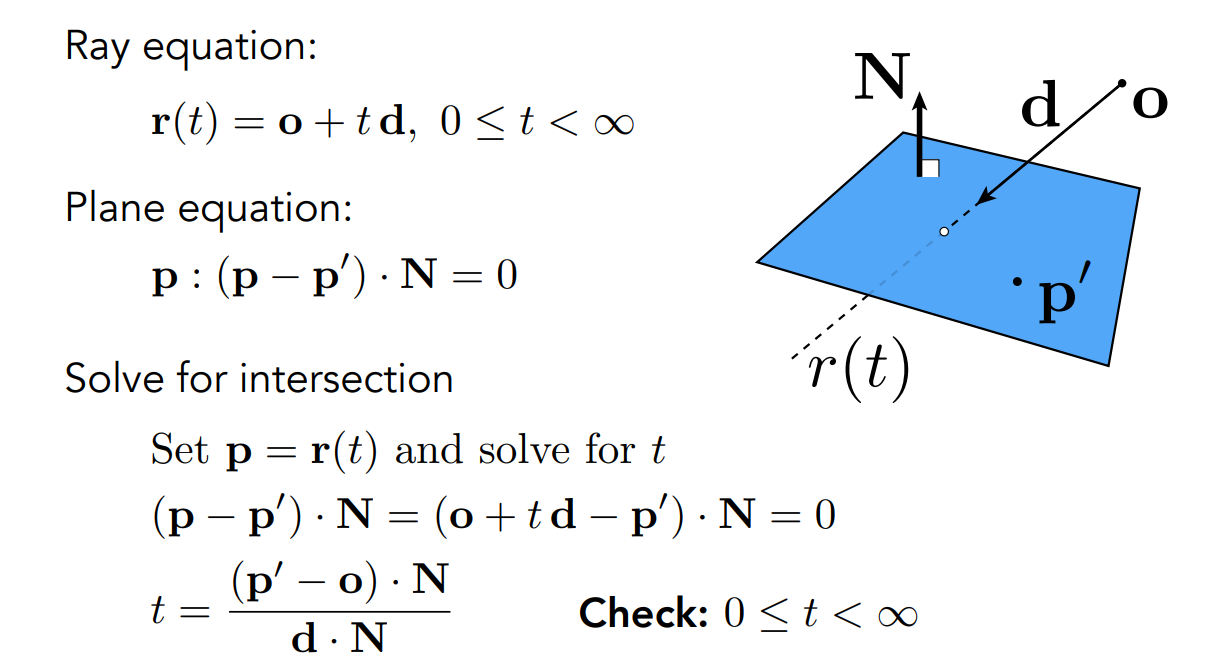
13.3.4.3 Moller Trumbore算法
- 用重心坐标表示平面:\((1-b_1-b_2)\vec{P_0} + b_1\vec{P_1} + b_2\vec{P_2}\)
- 判定点在射线上:\(t\ge 0\)
- 判定点在三角形内:\(b_1 \ge 0,b_2 \ge 0\)
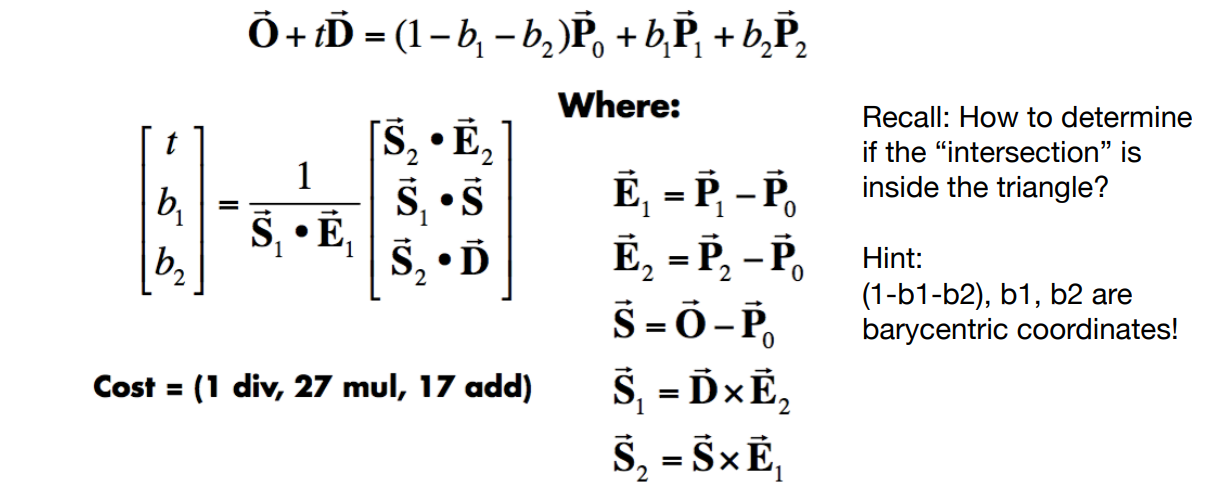
13.4 加速 光线 与 三角形表面 求交
13.4.1 包围盒 Bounding Volumes
- 用一个简单的形状,将物体包围起来,如果不能与包围盒相交,则一定不会与物体相交

13.4.2 轴对齐包围盒AABB:Axis-Aligned Bounding Box
空间中的长方体,可以理解为3对表面的交集
轴对齐包围盒:长方体的每一个边,均与坐标轴平行
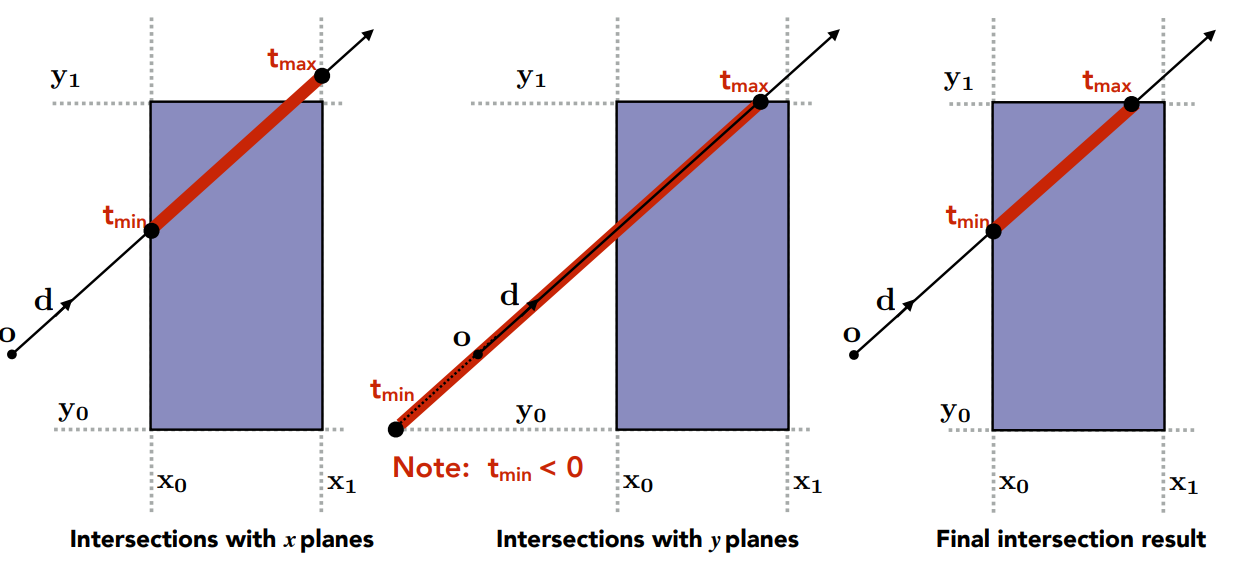
二维空间,光线与长方形求交
- 对于竖着的情况,可以得到在\(t=t_{x-min}\)时,与\(x=x_0\)相交;在\(t=t_{x-max}\)时,与\(x=x_1\)相交
- 对于横着的情况,可以得到在\(t=t_{y-min}\)时,与\(y=y_0\)相交;在\(t=t_{y-max}\)时,与\(y=y_1\)相交
- 由于长方形可以看作四条线的交集,因此光线在长方形中的部分,也可以看作\([t_{x-min},t_{x-max}]\)和\([t_{y-min},t_{y-max}]\)的交集
- 从而可以得到光线与长方形的交点对应的时间\(t_{enter} = \max(t_{x-min},t_{y-min})\),\(t_{exit}=\min(t_{x-max},t_{y-max})\)
三维空间,光线与长方体求交
- 只有当光线同时进入了3对表面,才能说光线进入了长方体
- 光线只要离开了1对表面,就说钢线离开了长方体
- 对于每一对表面,计算一次\([t_{min},t_{max}]\)
- 则对于长方体来说,\(t_{enter} = \max(t_{min})\),\(t_{exit}=\min(t_{max})\)
如果\(t_{exit}<0\),则说明盒子在光线的背后,不可能有交点
如果\(t_{exit}\ge0, t_{enter}<0\),则说明光线的起点在盒子里面,肯定有交点
因此,光线与AABB有交点,当且仅当:\(t_{enter}<t_{exit}\) 并且 \(t_{exit} \ge 0\)
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 华风夏韵!
评论