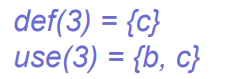一、Introduction

  1. 编译器是一个程序，用于将一种语言翻译成另一种语言

    1. 高级语言 => 高级语言/低级语言

    image-20230227102405818

  2. 编译器的特点：错误恢复，遇到error不是直接终止程序，而是会返回错误信息

  3. Phases：一个或多个模块，在编译过程中使用不同的抽象“语言”

  4. Interface：描述编译器模块之间交换的信息

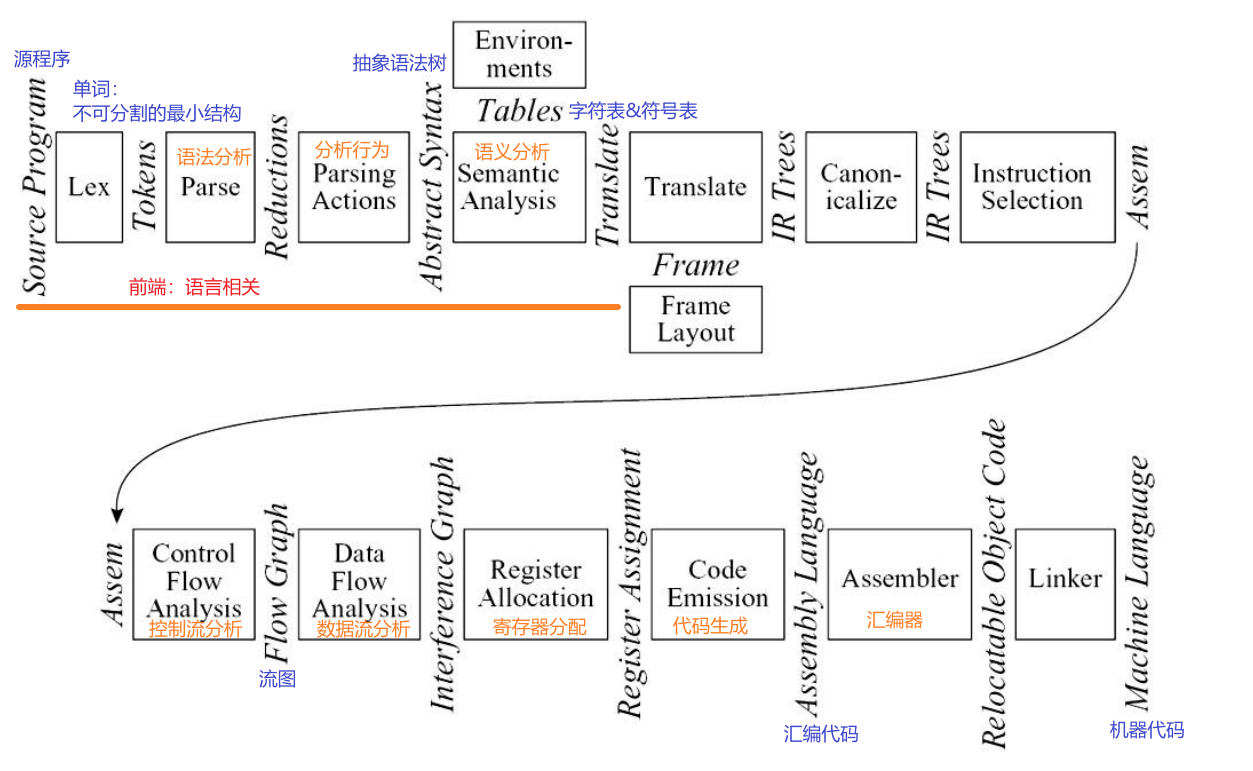
image-20230227104030169

1.1 模块和接口

阶段 解释
Lex：词法分析 将源代码分割为Tokens：正则语言
Parse：语法分析 分析程序的语法结构：上下文无关语言
Parsing Actions 根据每一个pharse，建立抽象语法树
Semantic Analysis：语义分析 确定每个短语的含义
将变量的使用与其定义联系起来
检查表达式类型
请求翻译每个短语
Frame Layout 将变量、函数参数等放入活动记录(栈帧)中
Translate 生成中间表示树(IR trees)
不与任何具体语言相关联
Canonicalize 提升表达式的副作用
清理条件分支
为了方便下一阶段
Instruction Selection 将IR树节点分组为与目标机器指令的操作相对应的块
Control Flow Analysis 将指令序列分析成控制流图，该图显示程序执行时可能遵循的所有可能的控制流
Dataflow Analysis 通过程序变量收集有关信息流的信息
例如，活跃度分析计算每个程序变量保持仍然需要的值（活跃）的位置
Register Allocation 选择一个寄存器来保存程序使用的每个变量和临时值
不同时存在的变量可以共享同一个寄存器
Code Emission 用机器寄存器替换每个机器指令中的临时名称
  1. 有些模块会被合并为一个模块：
    1. Parse，Semantic Analysis，Translate，Canonicalize
    2. Instruction Selection，Code Emission
  2. 简单的编译器可以省略：
    1. Control Flow Analysis，Data Flow Analysis，Register Allocation phases
  3. 数据结构：抽象语法树、IR tree、汇编序列
  4. 函数：抽象接口
    1. Lex：每次产生一个Token
    2. Parse：会调用Lex，获得一个Token，然后进行加工

1.2 工具和软件

  1. 两种抽象：
    1. 上下文无关语法：parsing
    2. 正则表达式：lexical analysis
  2. 两个工具
    1. Yacc：将上下文无关语法，转化为paing程序
    2. Lex：将正则表达式，转化为正则语言分析程序
    3. Yacc和Lex均会生成C语言程序

1.3 树形语言的数据结构

  1. 树形表示

    1. 主要表现形式
    2. 具有不同属性的多个节点类型
    3. 用类似编程语言的语法描述

    image-20230227110233280

  2. Concrete Tree：

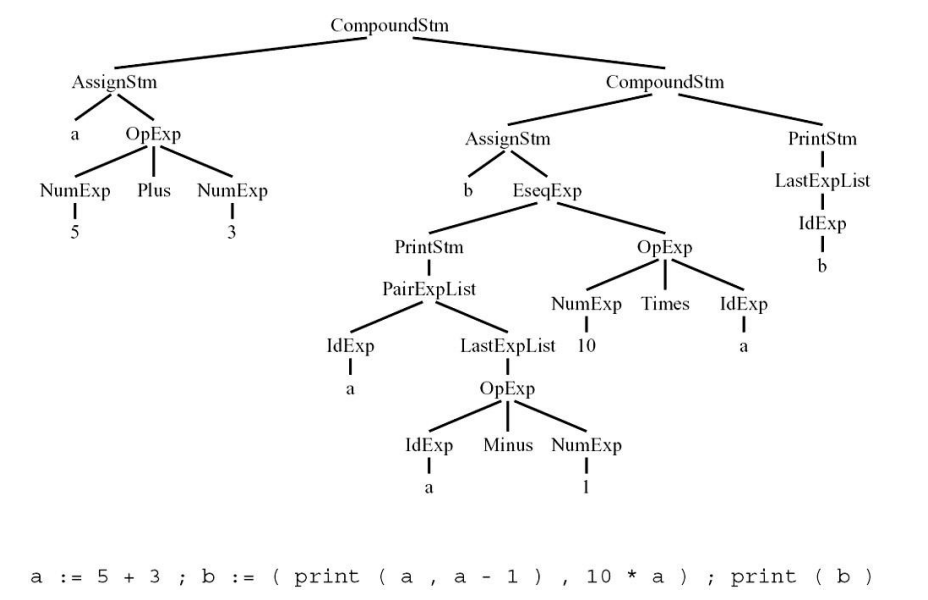
    image-20230227110445626

  3. 每个文法符号可以绑定一种类型，类型不固定

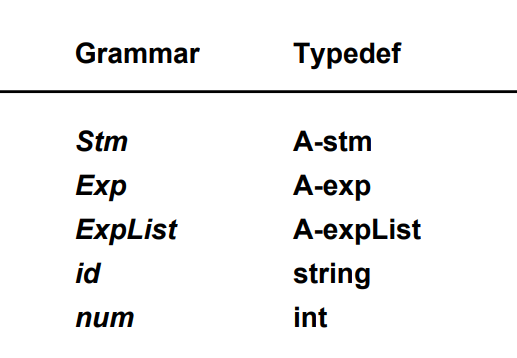
    image-20230227110554223

  4. 每一个语法规则：

    1. 一个构造函数：
      1. 属于左侧符号的联合
    2. 构造函数名称
      1. 显示在右侧–括号内
    3. 右侧部件
      1. 在数据结构中表示
      2. CompoundStm：在右侧有两个Stm
        1. Stm→ Stm; Stm
      3. AssignStm：具有标识符和表达式
        1. id:=Exp
    4. 每个语法符号的结构：
      1. 承载这些价值观的union，以及
      2. 一个种类字段，用于指示union的哪种表示是有效的

一、Introduction

  1. 编译器是一个程序，用于将一种语言翻译成另一种语言

    1. 高级语言 => 高级语言/低级语言

    image-20230227102405818

  2. 编译器的特点：错误恢复，遇到error不是直接终止程序，而是会返回错误信息

  3. Phases：一个或多个模块，在编译过程中使用不同的抽象“语言”

  4. Interface：描述编译器模块之间交换的信息

image-20230227104030169

1.1 模块和接口

阶段 解释
Lex：词法分析 将源代码分割为Tokens：正则语言
Parse：语法分析 分析程序的语法结构：上下文无关语言
Parsing Actions 根据每一个pharse，建立抽象语法树
Semantic Analysis：语义分析 确定每个短语的含义
将变量的使用与其定义联系起来
检查表达式类型
请求翻译每个短语
Frame Layout 将变量、函数参数等放入活动记录(栈帧)中
Translate 生成中间表示树(IR trees)
不与任何具体语言相关联
Canonicalize 提升表达式的副作用
清理条件分支
为了方便下一阶段
Instruction Selection 将IR树节点分组为与目标机器指令的操作相对应的块
Control Flow Analysis 将指令序列分析成控制流图，该图显示程序执行时可能遵循的所有可能的控制流
Dataflow Analysis 通过程序变量收集有关信息流的信息
例如，活跃度分析计算每个程序变量保持仍然需要的值（活跃）的位置
Register Allocation 选择一个寄存器来保存程序使用的每个变量和临时值
不同时存在的变量可以共享同一个寄存器
Code Emission 用机器寄存器替换每个机器指令中的临时名称
  1. 有些模块会被合并为一个模块：
    1. Parse，Semantic Analysis，Translate，Canonicalize
    2. Instruction Selection，Code Emission
  2. 简单的编译器可以省略：
    1. Control Flow Analysis，Data Flow Analysis，Register Allocation phases
  3. 数据结构：抽象语法树、IR tree、汇编序列
  4. 函数：抽象接口
    1. Lex：每次产生一个Token
    2. Parse：会调用Lex，获得一个Token，然后进行加工

1.2 工具和软件

  1. 两种抽象：
    1. 上下文无关语法：parsing
    2. 正则表达式：lexical analysis
  2. 两个工具
    1. Yacc：将上下文无关语法，转化为paing程序
    2. Lex：将正则表达式，转化为正则语言分析程序
    3. Yacc和Lex均会生成C语言程序

1.3 树形语言的数据结构

  1. 树形表示

    1. 主要表现形式
    2. 具有不同属性的多个节点类型
    3. 用类似编程语言的语法描述

    image-20230227110233280

  2. Concrete Tree：

    image-20230227110445626

  3. 每个文法符号可以绑定一种类型，类型不固定

    image-20230227110554223

  4. 每一个语法规则：

    1. 一个构造函数：
      1. 属于左侧符号的联合
    2. 构造函数名称
      1. 显示在右侧–括号内
    3. 右侧部件
      1. 在数据结构中表示
      2. CompoundStm：在右侧有两个Stm
        1. Stm→ Stm; Stm
      3. AssignStm：具有标识符和表达式
        1. id:=Exp
    4. 每个语法符号的结构：
      1. 承载这些价值观的union，以及
      2. 一个种类字段，用于指示union的哪种表示是有效的

三、语法分析 算法

3.1 LL(1)

S => uBDz
B => Bv
B => w
D => EF
E => y
E => 
F => x
F =>

3.1.1 nullable、First、Follow表的构建

非终止字符 nullable First Follow
S u
B w v, z， y, x
D true y, x z
E true y  x, z
F true x z

Follow()中，一定没有ε

First()中，可能有ε，对应nullable = true。有nullable时可以不写First()中的ε

nullable的计算方法：即该 non-terminal 可以推导出空串

  1.  表中红色：先看能够直接推出ε的规则，将规则左边的nullable项置为true
    1. E => ε，将E的nullable项置为ture
    2. F => ε，将F的nullable项置为ture
  2. 表中蓝色：然后判断剩余规则的右面，如果右面全为nullable，则左边的nullable项置为true
    1. D => EF，将D的nullable项置为ture

First的计算方法：即由该 non-terminal 能够推出的所有字符串中，可能的起始字符为谁

  1. 表中红色：先看规则的右边以 terminal 为起始的规则，则将该 terninal 添加进规则左边 non-terminal 的First()
    1. S => uBDz，将u添加进First(S)
    2. B => w，将w添加进First(B)
    3. E => y，将y添加进First(E)
    4. F => x，将x添加进First(F)
  2. 表中蓝色：然后看剩下的规则A => BC，则First(A) += First(B)；如果B可为空，则First(A) += First(C)
    1. D => EF, E可为空，则First(D) += First(E) ∪ First(F)

Follow的计算方法：即在所有可能的字符串中，可以在该 non-terminal 之后的第一个 terminal

  1. 表中红色：先看规则的右边，如果某个 non-terminal 后面直接跟了一个 terminal，则将该 terminal 添加进该 non-terminal 的Follow()
    1. S => uBDz, D可为空，将z添加进Follow(D)，将z添加进Follow(B)
    2. B => Bv，将v添加进Follow(B)
  2. 表中蓝色：然后看剩下的规则A => BC，则Follow(B) += First(C), Follow(C) += Follow(A)；如果C可为空，则Follow(B) += Follow(A)
    1. S => uBDz，则Follow(B) += First(D)
    2. D => EF, F可为空，则Follow(F) += Follow(D)，Follow(E) += Follow(D)

3.1.2 构建LL(1) Parsing Table

表的作用：给定当前状态、下一个读到的终止字符，可以判定使用哪一条规则继续递归

u z v w x y
S S=>uBDz
B B=>Bv, B=>w
D D=>EF D=>EF D=>EF
E E=> ε E=> ε E=>y
F F=> ε F=>x

对于所有的推导规则A => α：

  1. 表中红色：找出First(α)中包含的所有终止字符t，则T[A,t] = (A=>α)
    1. S => uBDz：First(uBDz) = u，则T[S,u] = (S=>uBDz)
    2. B => Bv：First(Bv) = w，则T[B,w] = (B=>Bv)
    3. B => w：First(w) = w，则T[B,w] = (B=>w)
    4. D => EF：First(EF) = x,y，则T[D,x] = T[D,y] = (D=>EF)
    5. E => y：First(y) = y，则T[E,y] = (E=>y)
    6. F => x：First(x) = x，则T[F,x] = (F=>x)
  2. 表中蓝色：如果α可为空，则找出Follow(A)中包含的所有终止字符t，则T[A,t] = (A=>α)
    1. D => EF：EF可为空，Follow(D) = z，则T[D,z] = (D=>EF)
    2. E =>：Follow(E) = x,z，则T[E,x] = T[E,z] = (E=>)
    3. F =>：Follow(F) = z，则T[F,z] = (F=>)

3.1.3 判断是否为LL(1)文法

核心思路：LL(1) Parsing Table中，某一个项对应多个值

  1. 表中红色：对于所有规则A=>α, A=>β，如果\(First(\alpha)\cap First(\beta) \neq \{\}\)，则不是LL(1)
    1. 不能存在左公因子
  2. 表中蓝色：对于所有的可为空的非终止字符A，如果\(First(A)\cap Follow(A) \ne \{\}\)，则不是LL(1)

3.1.4 将文法修改为LL(1)文法：左递归消除

原来的文法：

  1. \(S \rightarrow S\alpha_1 |...|S\alpha_n\)
  2. \(S \rightarrow \beta_1|...|\beta_m\)

更改为：

  1. \(S \rightarrow \beta_1S' |...| \beta_mS'\)
  2. \(S' \rightarrow \alpha_1S' | ... | \alpha_nS'|\epsilon\)

3.2 LR(0) & SLR(1)

S => X$
X => Ma
X => bMc
X => dc
X => bda
M => d

3.2.1 构造LR(0)状态机

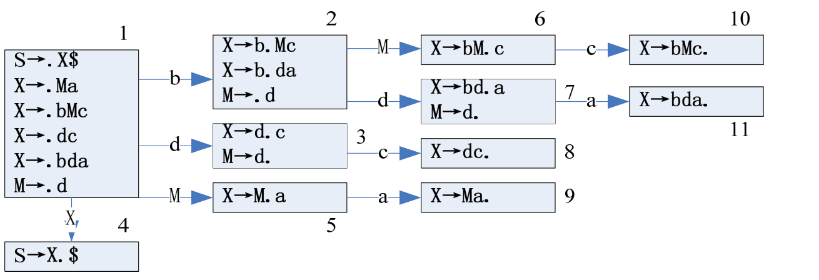
image-20230326220719577

保证与起始字符相关的转移规则只有一条，如果不唯一，则新增一个起始字符

  1. 首先，构造起始字符的LR(0)Item，设为状态1
    1. 先将起始字符的唯一一条转移规则，写到状态1里面
      1. S => .X$
    2. 对于状态1中所有的.后面为非终止字符的情况，将终止字符展开，写入状态1里面
      1. 展开X：X => .Ma、X => .bMc、X => .dc、X => .bda
      2. 展开M：M => .d
    3. 如果有一条语句为A => ε，则在Item中的表示为：A => .
  2. 对于所有的状态，从上到下根据.后面的字符，接收该字符，转移到新的状态(没有则无法转移)
    1. 如状态1可以接收b，转移到状态2，对应.向后移一位，即X => b.Mc, X => b.da
    2. 对于新增的状态，类似状态1，进行展开
      1. 如状态2原本是X => b.Mc , X => b.da，但是M为非终止符，需要展开为：M => .d
  3. 直到没有新的状态产生

3.2.2 构造LR(0) Parsing Table

表的内容

  1. sk：将对应的终止字符压栈，然后转移到状态k
  2. gk：将对应的非终止字符压栈，然后转移到状态k
  3. rk：使用第k条规则规约
  4. accept：接受该字符串

表的创建方式：

  1. 对于DFA中的每一个Si 接受终止符t 转移到Sj，令T[i, t] = sj（Input & Shift表）
  2. 对于DFA中的每一个Si 接受非终止符X 转移到Sj，令T[i, X] = gj（Goto表）
  3. 对于每一个可以规约的LR(0) Item，对于其所在所有状态i，每一个终止字符t，令T[i, t] = rk，k为对应规则的编号

3.2.3 构造SLR Parsing Table

首先，求出所有非终止字符的Follow()

  1. Follow(S) = {$}
  2. Follow(E) = {=, $}
  3. Follow(V) = {=, $}

构建SLR(1) Parsing Table：

  1. 对于DFA中的每一个Si 接受终止符t 转移到Sj，令T[i, t] = sj（Input & Shift表）
  2. 对于DFA中的每一个Si 接受非终止符X 转移到Sj，令T[i, X] = gj（Goto表）
  3. 对于每一个可以规约的LR(0) Item (假设为A => α)，对于其所在所有状态i，每一个终止字符t，如果t ∈ Follow(A)，则令T[i, t] = rk，k为对应规则的编号

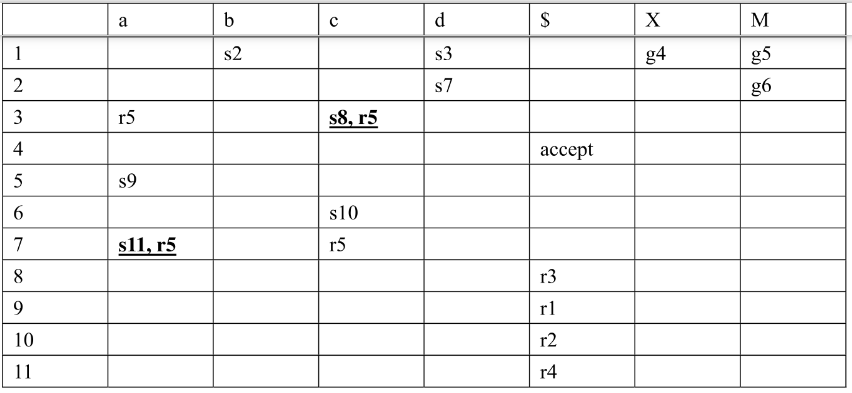
image-20230326223403239

3.3 LR(1) & LALR(1)

S => X$
X => Ma
X => bMc
X => dc
X => bda
M => d

3.3.1 构造LR(1)状态机

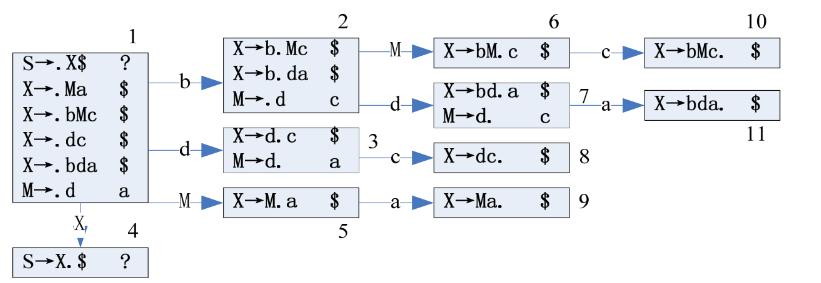
image-20230326220621532

保证与起始字符相关的转移规则只有一条，如果不唯一，则新增一个起始字符

  1. 首先，构造起始字符的LR(1)Item，设为状态1
    1. 先将起始字符的唯一一条转移规则，写到状态1里面，并将向前看字符设置为$
      1. S => .X$ ?
    2. 对于状态1中所有的.后面为非终止字符的情况，将非终止字符展开，写入状态1里面，向前看字符为展开非终止字符时，后面的串的First()
      1. 根据S => .X$ ?展开X：
        1. X => .Ma $、X => .bMc $、X => .dc $、X => .bda $
      2. 根据X => .Ma $展开M：
        1. M => .d a
  2. 对于所有的状态，从上到下根据.后面的字符，接收该字符，转移到新的状态，且向前看字符不变(.没有字符则无法转移)
    1. 如状态1可以接收b，转移到状态2，对应.向后移一位
      1. 即X => b.Mc $, X => b.da $
    2. 对于新增的状态，类似状态1，进行展开
      1. 如状态2原本是X => b.Mc $, X => b.da $，但是M为非终止符，需要展开为：M => .d c
  3. 直到没有新的状态产生

3.3.2 构造LR(1) Parsing Table

  1. 对于DFA中的每一个Si 接受终止符t 转移到Sj，令T[i, t] = sj（Input & Shift表）
  2. 对于DFA中的每一个Si 接受非终止符X 转移到Sj，令T[i, X] = gj（Goto表）
  3. 对于每一个可以规约的LR(1) Item，对于其所在所有状态i，每一个向前看字符t，令T[i, t] = rk，k为对应规则的编号

3.3.3 构造LALR(1) Parsing Table

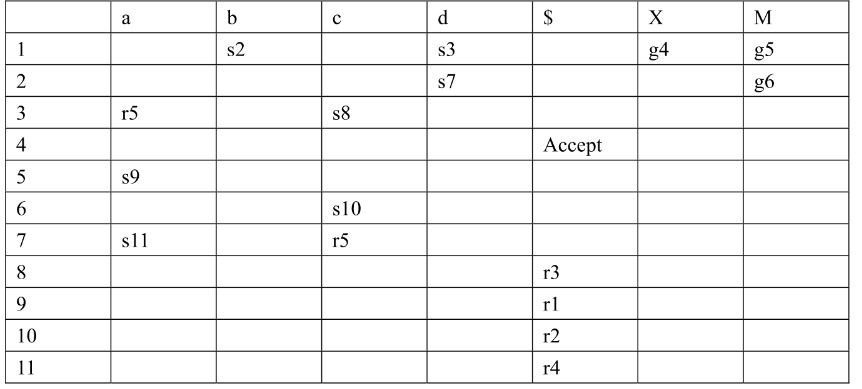
image-20230326223155255

  1. 将LR(1)状态机中，LR(0)部分相同的状态合并，得到LALR(1)状态机
  2. 在根据LALR(1)状态机，仿照构造LR(1)的规则，构造LALR(1)分析表

3.4 将BNF转换为EBNF

3.4.1 {}表示循环

BNF：exp => exp '+' term | term

EBNF：exp => term {'+' term}

void exp(){
    term();
    while(token == '+'){
        eat(token);
        term();
    }
}

3.4.2 []表示选0/1次

BNF：IF => if ( exp ) statement | if ( exp ) statement else statement

EBNF：IF => if ( exp ) statement [else statement]

三、Parsing

3.1 上下文无关语法 CFG

3.1.1 Parser的任务

image-20230306114328968

  1. 输入：tokens流
  2. 输出：抽象语法树

3.1.2 CFG的表示

  1. 符号：
    1. terminals：终止符
    2. non-terminals：非终止符
  2. 起始符号
  3. 规则：符号 → 符号 符号 ... 符号
    1. 左边：non-terminal
    2. 右边：termials 和 non-terminals 的连接
    3. 右边的符号可以视为左边符号的解释

3.1.3 CFG的推导

  1. 从起始符号开始
  2. 如果存在非终止符号，选择一个规则，用右边的符号替代左边的符号
  3. 重复2，直到只有终止符

整个推导过程，可以形成一个抽象语法树 abstract syntax tree

示例

image-20230306115739759

image-20230306120038013

3.1.4 Parse Tree

  1. concrete syntax：即为Parse Tree，分析过程中的所有结果均会保留
  2. abstract syntax：删除所有对分析结果没有影响的路径

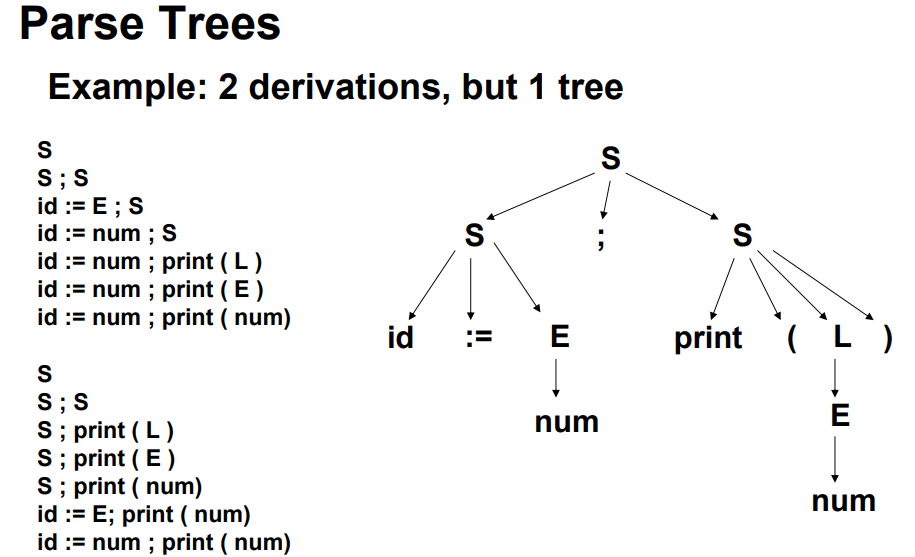
image-20230306120406480

3.1.5 Ambiguous Grammar

  1. 给定的某个tokens的序列，可以得到两个不同的parse tree

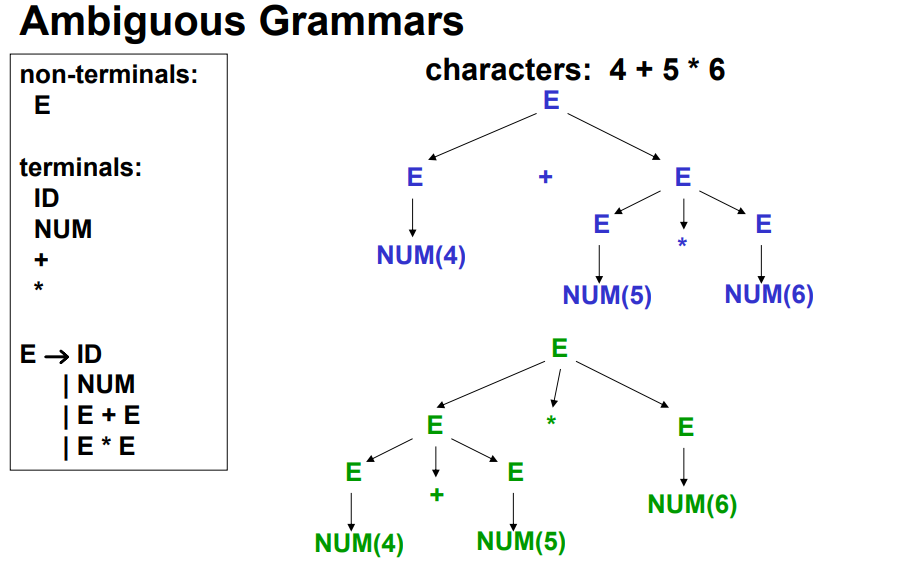
image-20230306121006118

3.1.6 消除歧义

  1. 添加优先级：离根越远，优先级越高
  2. 改造文法

image-20230306121521468

3.1.7 End-of-File标识符：$

image-20230306121656796

  1. 使用$表示文件结束
  2. 使用S表示表达式的起始状态

3.2 自顶向下分析：Predictive Parsing

LL(k)：

  1. Left-to-right parse：从左到右分析
  2. Leftmost-derivation：最左推导
  3. 1 symbol lookahead：向前看1个符号

3.2.1 递归下降分析法：LL(k)

  1. 可以分析很多CFG，但不是所有的
  2. 关键思想
    1. 每一个非终结符，视为一个递归函数
    2. 每一次推导，视为函数中的一个语句

image-20230313100635454

image-20230313100648772

image-20230313100700565

3.2.2 存在问题：无法解决直接左递归的情况

  1. 预测分析仅适用于：输入中的第一个终止符号提供足够的信息来选择要使用哪种生成的语法
  2. 在解析L时，如果tok=ID，解析器无法确定要使用哪个生成方式

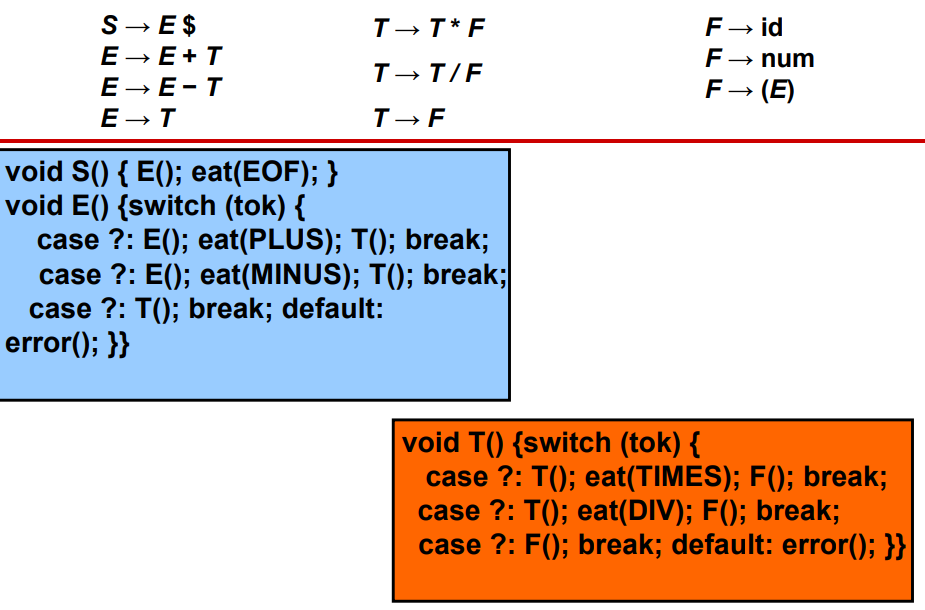
image-20230313100955345

3.2.3 X是否可生成ε：Nullable(X)

  1. \((X:=\epsilon)\)，则\(X\)为\(Nullable\)
  2. \((X:=ABC...)\)，且\(A,B,C...\)均为\(Nullable\)，则\(X\)为\(Nullable\)

3.2.4 X可生成的第一个终结符：First(X)

看规则的左边

  1. 如果\(T\)为终结符，则\(First(T)=\{T\}\)
  2. 如果\(X\)为非终结符，且\((X:=ABC...)\)，则\(First(X)=First(ABC...)\)
    1. \(First(ABC...)=F1 \cup F2 \cup F3 ...\)
    2. \(F1 = Fisrt(A)\)
    3. 如果A为\(Nullable\)，则\(F2=First(B)\)；否则\(F2=\epsilon\)
    4. 如果A、B为\(Nullable\)，则\(F3=First(C)\)；否则\(F3=\epsilon\)

3.2.5 X后面可以跟的第一个终结符：Follow(X)

看规则的右边

  1. 给出语法的第一个规则的左边，默认为起始符号
  2. 对于起始符号，添加一个$进入Follow集合中，$表示输入的结束
  1. 初始化：\(Follow(X):=\{\}\)
  2. 如果\((Y:=s1 X s2)\)，则\(Follow(X)=First(s2)\)
  3. 如果\((Y:=s1Xs2)\)，且\(s2\)为\(Nullable\)，则\(Follow(X)=Follow(Y)\)

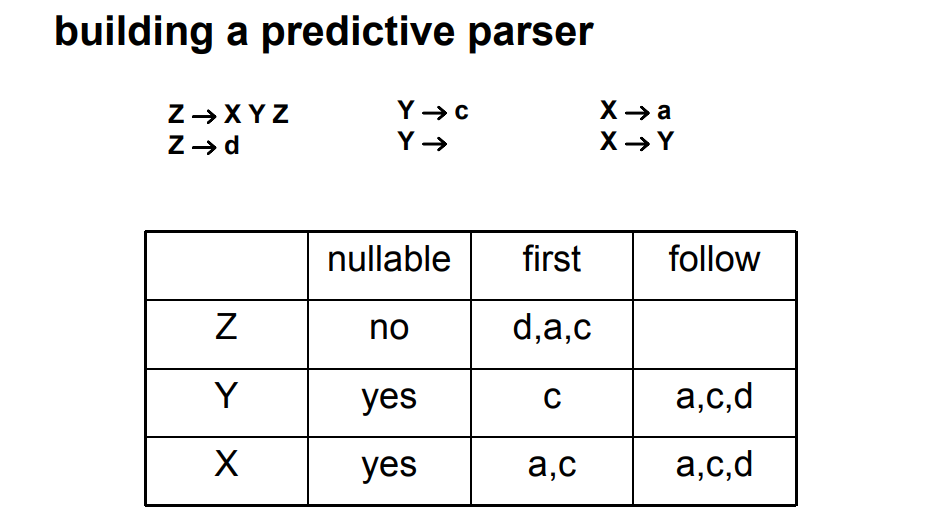
image-20230313102750425

3.2.6 分析表 Parsing Table

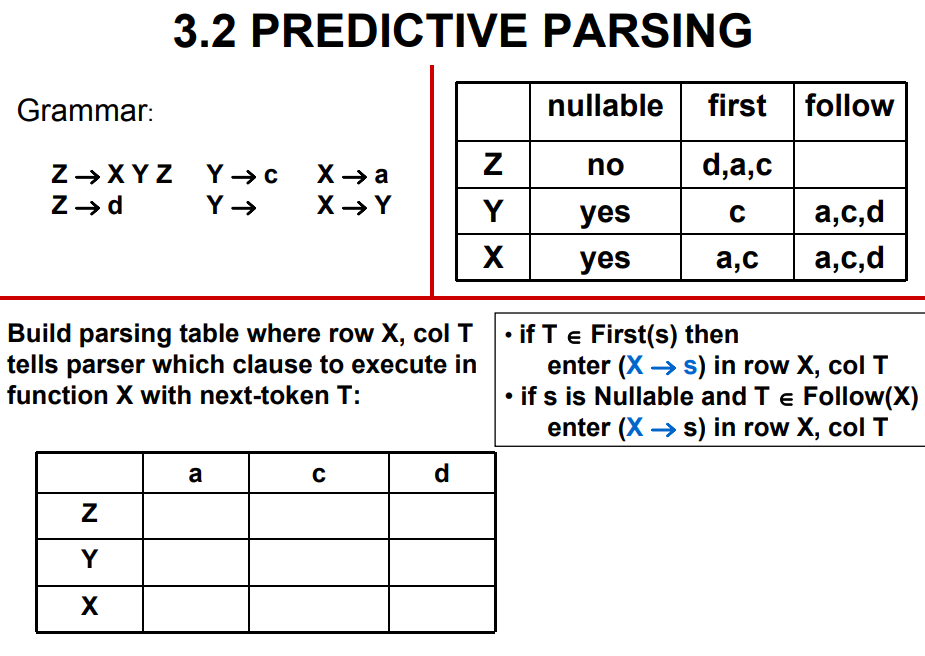
image-20230313103442922

image-20230313103514872

  1. 构造分析表：对于规则\((X=>s)\)
    1. 如果\(T\in First(s)\)，则在\(X\)行\(T\)列，填入\((X=>s)\)
    2. 如果\(s\)为\(Nullable\)，且\(T\in Follow(X)\)，则在\(X\)行\(T\)列，填入\((X=>s)\)
  2. 匹配文法：
    1. 终结符：匹配
    2. 非终结符：查表
      1. 如果当前的非终结符为\(Z\)，读到的token为\(a\)，则使用\(Z=>XYZ\)的规则
      2. 如果没有产生式，则输入有语法错误
      3. 如果有多个产生式，则当前语法有歧义

3.2.7 LL(1)

  1. 如果以这种方式构造的预测分析表不包含重复条目，则语法称为LL(1)

  2. 判定语法是否为LL(1)：

    1. 对于所有的\(A\)，如果\(\epsilon \in First(A)\)，如果\(First(A)\cap Follow(A) \ne \{\}\)，则不是LL(1)
    2. 对于所有的A=>α，A=>β，如果\(First(\alpha)\cap First(\beta) \neq \{\}\)，则不是LL(1)
    3. 否则，是LL(1)

  3. LL(k)：即往前看k个符号

    image-20230313104247750

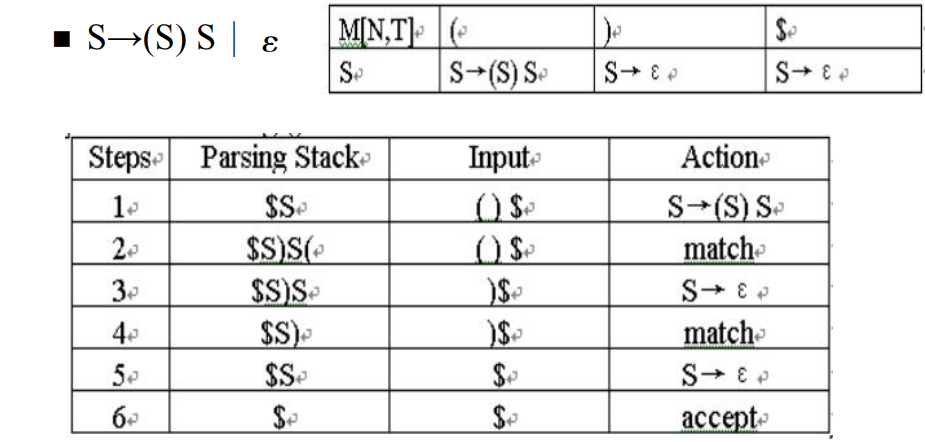
  4. 示例：

    1. 注意替换后，右边的string要倒序进栈
    2. accept表示当前字符串，可以被接受

    image-20230313104432448

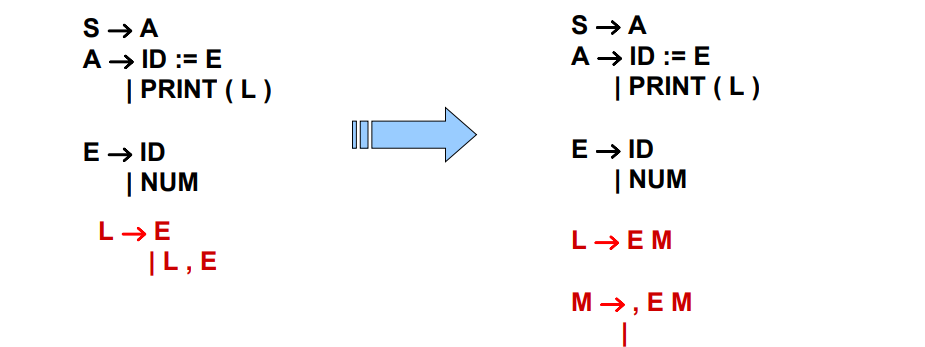
3.2.8 解决左递归问题

3.2.8.1 消除左递归

  1. 添加新的规则，消除左递归

    image-20230313104825289

  2. 示例：

    image-20230313104711778

3.2.8.2 四则运算的语法

image-20230313104931063

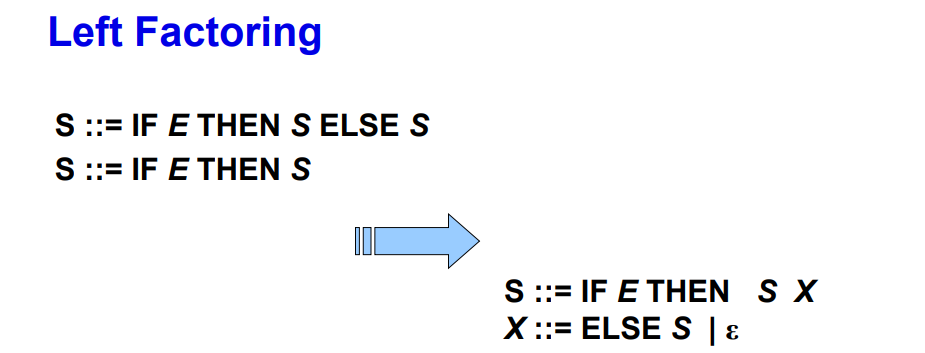
3.2.9 解决左公因子问题

  1. 将判定推迟，在拿到ELSE时，才判断使用哪个规则
    1. 原来为：\(A=>\alpha\beta,A=>\alpha\gamma,A=>\alpha\)
    2. 改造为：\(A=>\alpha A', A'=>\beta|\gamma|\epsilon\)
  2. 示例：

image-20230313105125827

3.2.10 错误恢复

  1. 当产生错误时：

    1. 产生异常，退出生成过程

      image-20230313105839095

    2. 输出错误信息，从错误中恢复：

      1. 删除token：

        1. 最安全的，因为避免了错误的放大
        2. 删除token，直到读到了\(Follow\)集合中的token

        image-20230313105904507

        image-20230313110110363

      2. 替换token

      3. 增加token

3.3 自底向上分析：Bottom-up(Shift-Reduce) Parsing

  1. LL(k)：必须向前看k个符号，才能决定执行哪一步操作
  2. LR(k)：不需要向前看，在k一定时分析能力更强
    1. Left-to-right parse：从左到右分析
    2. Rightmost-derivation：最右推导
    3. 1 symbol lookahead：向前看1个符号

3.3.1 LR(k)

  1. 语法器跟踪了：
    1. 位于当前输入的哪个位置，即下一个要读入的input
    2. 一个包含终止符&非终止符的栈，表示当前已经生成的语法
  2. 四种操作：
    1. shift：将下一个输入放到栈顶
    2. reduce R：栈顶匹配了规则的RHS，则将栈顶替换为LHS
    3. error
    4. accept：栈里面只有开始符号时，生成成功

3.3.2 LR生成表

  1. sn：shift，然后转为状态n
  2. gn：转为状态n
  3. rk：reduce，使用规则k
  4. a：accept，要保证唯一
  5. 空：error

image-20230313113747529

3.3.3 Shift-Reduce Algorithm

使用一个整数，表示当前的生成状态

  1. 整数表示FA的一个状态
  2. 可以通过在当前解析堆栈上运行自动机来计算当前解析状态

image-20230313115149751

3.3.4 LR(0)解析器

  1. LR(0) item：如果点号的右面为非终结符，则将其使用规则替换
  2. complete item：点号在最右面，只能进行reduce操作，如状态2
  3. shift item：点号不在最右面，需要进行shift操作

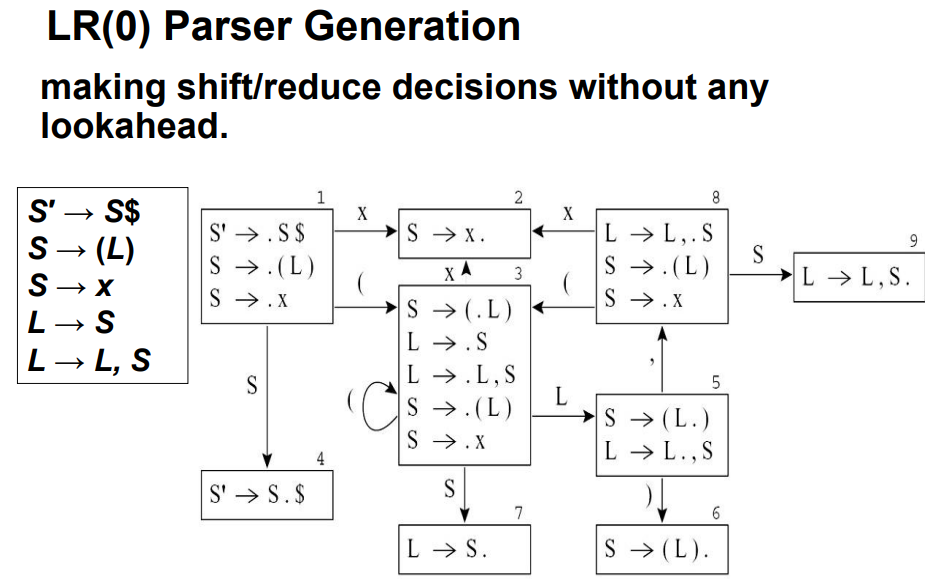
image-20230313114753200

image-20230313115118645

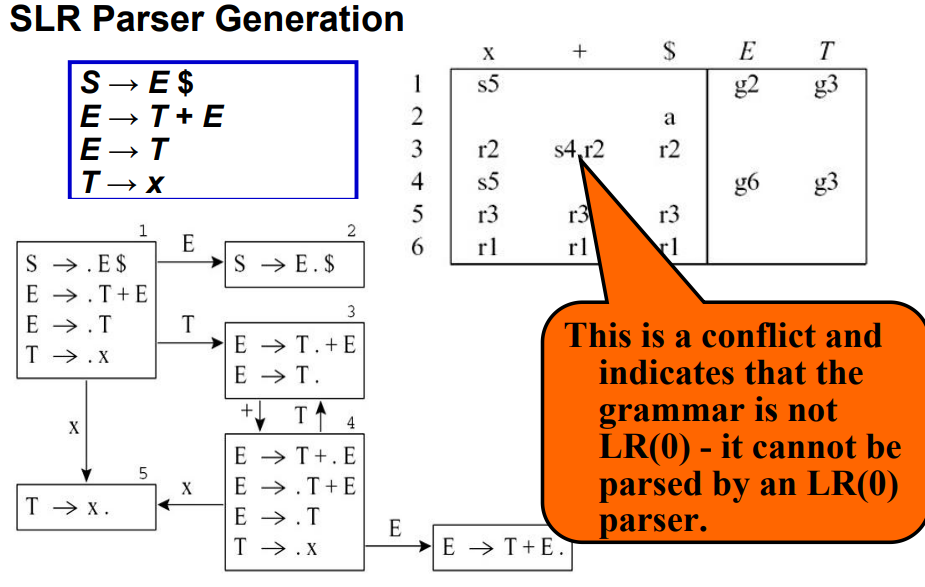
LR(0)解析器无法解决的问题：SLR

image-20230313115402787

3.3.5 SLR解析器

image-20230313115707940

3.3.6 LR(1)解析器

  1. LR(1) item：LR(0) item + lookahead symbol(一个终结符)

    image-20230313120317158

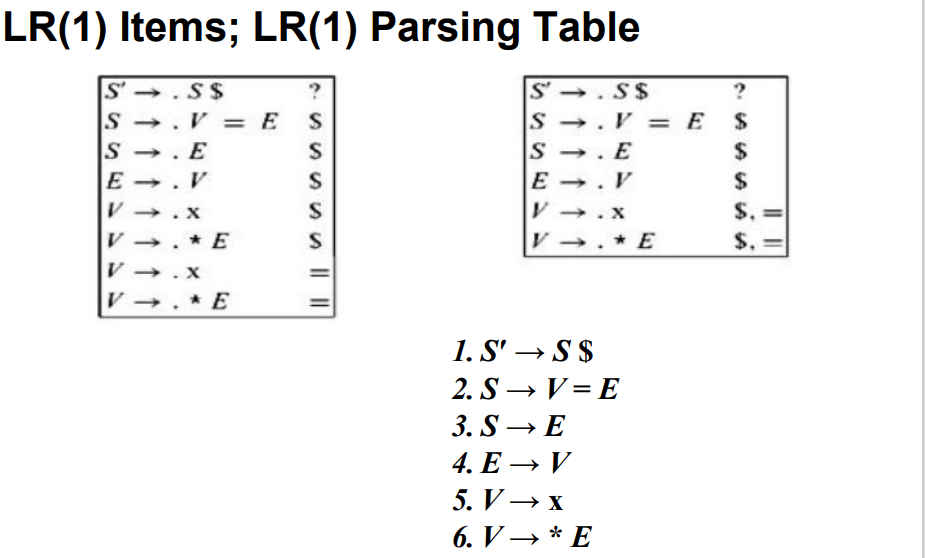
    image-20230313120458869

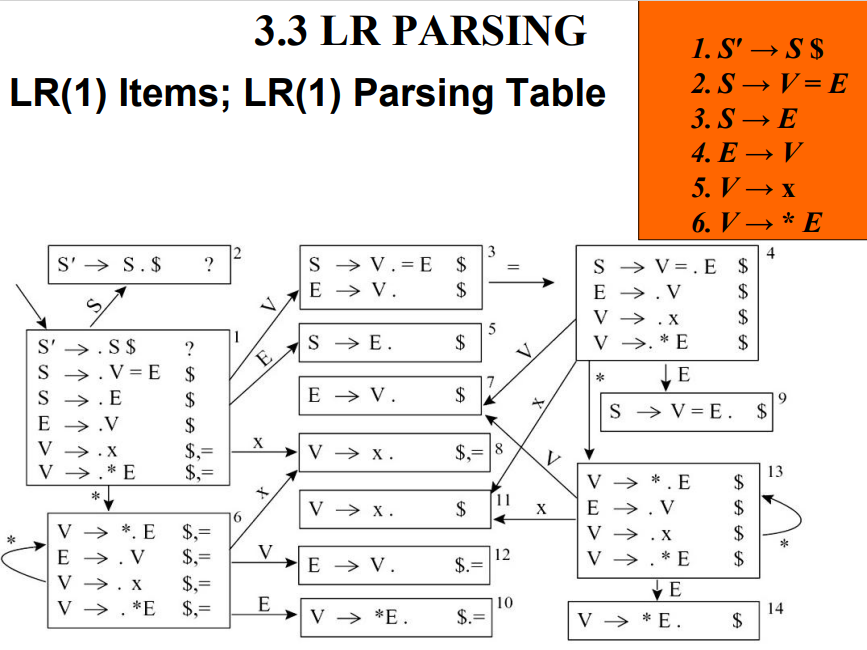
    image-20230320101521894

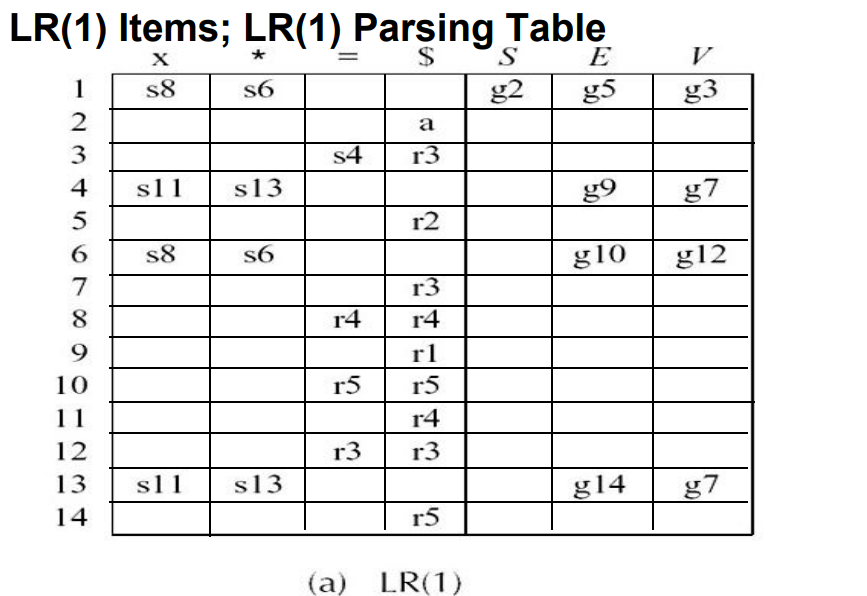
    image-20230320101933691

  2. 判断文法是否有冲突(歧义)

    Shift项：点号在中间

    Reduce项：点号在最右边，也称为完整项

    1. shift-reduce冲突：shift项和reduce项在同一个状态中
    2. reduce-reduce冲突：向前看符号相同的reduce项和reduce项在同一个状态中
    3. 在LR(1) Parsing Table中，有某个表项中存在2个动作

3.3.7 LALR(1)解析器

  1. LR(0)的部分是相同的
  2. 前面一样但lookahead项不同的状态，合并起来
  3. 直接构造LALR(1)的算法不做要求
  4. 会使文法的表达能力下降：新增加了reduce-reduce冲突

image-20230320102337824

3.3.8 不同语法的分析能力

image-20230320102923215

3.3.9 歧义文法

image-20230320103243931

  1. 改造文法：引入非终结符M

    image-20230320103410977

  2. 添加优先级

3.4 YACC

Yet Another Compiler Compiler

  1. 可以将动作放在中间

    image-20230320111844718

  2. 消除歧义的规则

    1. 定义字符的结合方式：左结合%left，右结合%right，不结合%nonassoc

    2. 优先级：定义的越后面，优先级越高

            %left '+''-'
            %left '*'

         3. 规则的优先级，由产生式的最后一个符号决定

         4. 当规则的优先级相同时，如果符号为左结合，则选择`reduce`，如果符号为右结合，则选择`shift`，如果符号为不结合，则报错`error`

         5. 可以使用`%prec`定义优先级

         <img src="https://raw.githubusercontent.com/unicorn2022/Pictures/main/AssetMarkdown/image-20230320112549063.png" alt="image-20230320112549063" style="zoom:80%;" />

      <img src="https://raw.githubusercontent.com/unicorn2022/Pictures/main/AssetMarkdown/image-20230320112933865.png" alt="image-20230320112933865" style="zoom:80%;" />

      ## 3.5	错误恢复

      ### 3.5.1	局部错误恢复

      1. 局部错误恢复机制：

         1. 在检测到错误时调整解析堆栈和输入，以允许恢复解析

      2. yacc：使用`error`通配符，使得文法分析能够通配

         <img src="https://raw.githubusercontent.com/unicorn2022/Pictures/main/AssetMarkdown/image-20230320113349913.png" alt="image-20230320113349913" style="zoom:80%;" />

      3. error的使用：

         <img src="https://raw.githubusercontent.com/unicorn2022/Pictures/main/AssetMarkdown/image-20230320113559921.png" alt="image-20230320113559921" style="zoom:80%;" />

         > 示例：
         >
         > <img src="https://raw.githubusercontent.com/unicorn2022/Pictures/main/AssetMarkdown/image-20230320113644205.png" alt="image-20230320113644205" style="zoom:80%;" />
         >
         > <img src="https://raw.githubusercontent.com/unicorn2022/Pictures/main/AssetMarkdown/image-20230320113706224.png" alt="image-20230320113706224" style="zoom:80%;" />
         >
         > <img src="https://raw.githubusercontent.com/unicorn2022/Pictures/main/AssetMarkdown/image-20230320113731521.png" alt="image-20230320113731521" style="zoom:80%;" />

      ### 3.5.2	全局错误恢复

      <img src="https://raw.githubusercontent.com/unicorn2022/Pictures/main/AssetMarkdown/image-20230320114142228.png" alt="image-20230320114142228" style="zoom:80%;" />

      <img src="https://raw.githubusercontent.com/unicorn2022/Pictures/main/AssetMarkdown/image-20230320114244565.png" alt="image-20230320114244565" style="zoom:80%;" />

      ## 3.6	区分LR(0),SLR,LR(1)

      根据reduce操作区分

      1. `LR(0)`：同一行中有同一个reduce，且重复多次
      2. `LR(1)`：同一个reduce可能出现在不同行
      3. `SLR`：同一个reduce只能出现在一行

       

      # 四、抽象语法树 AST

      1. 降低语法树的存储开销
      2. 一定程度上过滤掉不同语法的差异

      ## 4.1	语义动作 Semantic Actions

      所有的终结符和非终结符都会关联到它自己的语义属性

      1. 例如：`A => BCD`
      2. 语义操作必须返回一个值，该值的类型为与非终结符`A`关联的类型
      3. 它可以根据与匹配的终结符和非终结符`B、C、D`相关联的值来构建该值
      4. B的属性也可能依赖于CD

      ### 4.1.1	递归下降分析 Recursive Descent

      ```tex
      S  => E$
      E  => TE'
      E' => +TE'
      E' => -TE'
      E' => 
      T  => FT'
      T' => *FT'
      T' => /FT'
      T' => 
      F  => id
      F  => num
      F  => (E)

image-20230327102513916

image-20230327102654495

4.1.2 YACC生成树

  1. Yacc生成的解析器通过维护两个栈（状态栈、value栈）并行来实现语义值
  2. 当解析器执行归约时，它必须执行C语言语义操作
  3. 当解析器从状态栈中弹出前k个元素并压入非终结符时，它也从value栈中弹出k个元素并压入通过执行语义动作获得的值

image-20230327102803796

4.2 抽象语法树 Abstact Parse Trees

  1. parse tree：编译器的后续阶段可以遍历的数据结构。
    1. 输入的每个token正好有一个叶节点
    2. 对于在解析过程中使用的每个语法规则有一个内部节点
  2. concrete parse tree：表示源语言的具体语法
  3. abstract syntax：抽象语法树传达了源程序的短语结构，解决了所有解析问题，但没有任何语义解释
  4. abstract在解析器和编译器后面的短语之间建立了一个干净的接口
  5. 解析器使用具体语法树为抽象语法构建抽象语法树。语义分析阶段采用这个抽象的语法树

image-20230327104140072

image-20230327104154280

image-20230327104204667

4.2.1 Positions

  1. 如果存在必须向用户报告的type error，则词法分析器的current position是错误源位置的合理近似值
  2. 对于one-pass编译器，词法分析器会保留一个全局变量current position
    1. one-pass：对代码、语法树等均只进行一次扫描
  3. 使用抽象语法树数据结构的编译器需要准确地记住位置
  4. pos字段指示从中派生出这些抽象语法结构的字符的位置
  5. 使用Yacc时，一种解决方案是定义一个非终结符pos，其语义值是源位置（行号或行号和行内位置）

image-20230327104917987

4.3 EBNF：扩展BNF

只要文法满足EBNF，则一定可以递归下降分析，一定没有左递归和左公因子

image-20230327105501746

{}：表示循环

image-20230327105513052

image-20230327105523638

在代码中处理左结合问题

image-20230327105715790

[]：表示选0/1次

image-20230327105751653

其他问题

image-20230327110035417

五、语义分析

  1. 将变量的定义和使用联系起来
  2. 检查每一个表达式是否拥有正确的类型
  3. 将抽象语法树转化成一种更为简单的表示形态，用于后续生成机器代码

5.1 符号表 Symbol Table

5.1.1 符号表

  1. 符号表用于将标识符映射到其类型、位置
  2. 环境是一组绑定，使用↦表示
    1. σ0：表示函数外的环境
    2. +：表示扩展符号表
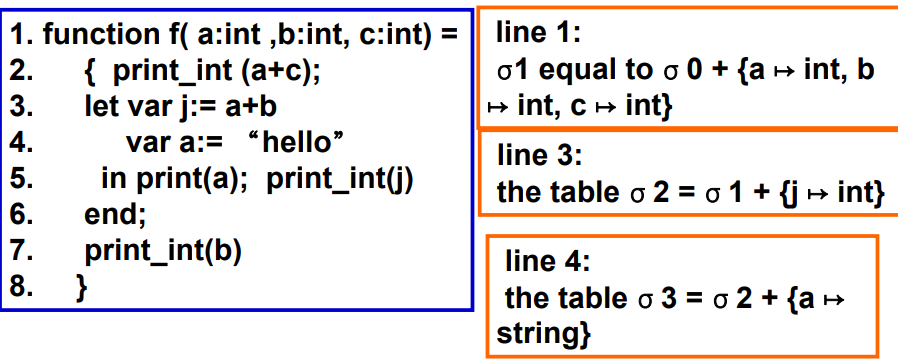
    3. 符号表是动态的，每一条语句都有可能改变符号表
  3. +：X+Y与Y+X不同，因为如果存在相同符号，+后面的符号表会覆盖前面的符号表
    1. 函数式风格：当创建σ2、σ3时，不会更改σ1的值
    2. 命令式风格：修改σ1直到其变为σ2，当使用σ2时无法查看σ1，σ2失效时，需要通过undo操作将其更改为σ1

image-20230327111828986

5.1.2 多个符号表

有些语言可以同时有多个不同的符号表：

  1. 如程序中的每个module、class、record均可有各自的符号表σ

image-20230327112550410

5.1.3 符号表的构造

使用Hash表+单链表构造符号表，每次将值插入表头

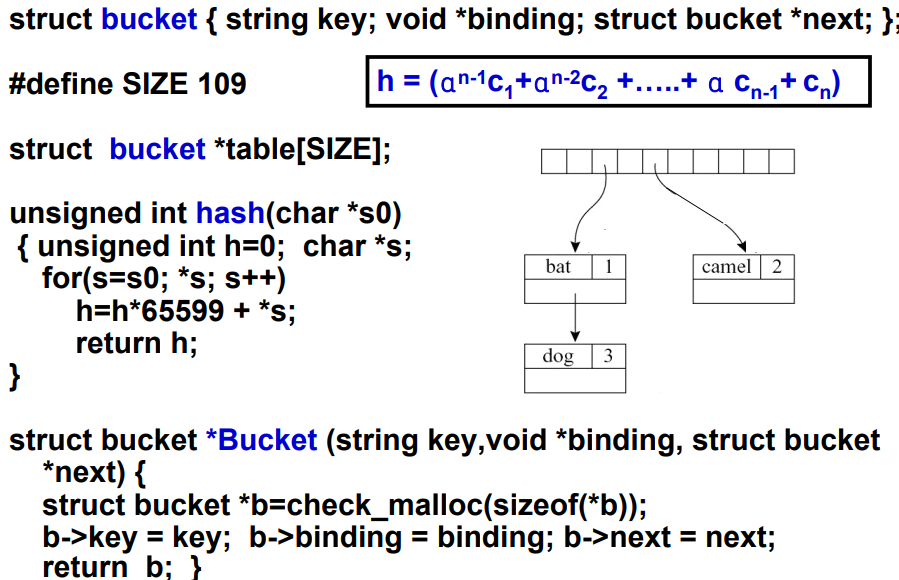
image-20230327113230230

image-20230327113540284

  1. 如果σ + {a ↦ T2}，而σ已经包含了{a ↦ T1}，由于将{a ↦ T2}放到了表头
    1. 当查询时，找到第一个{a ↦ T2}就返回了，不会查到之前的{a ↦ T1}
    2. 删除时，也是找到第一个{a ↦ T2}

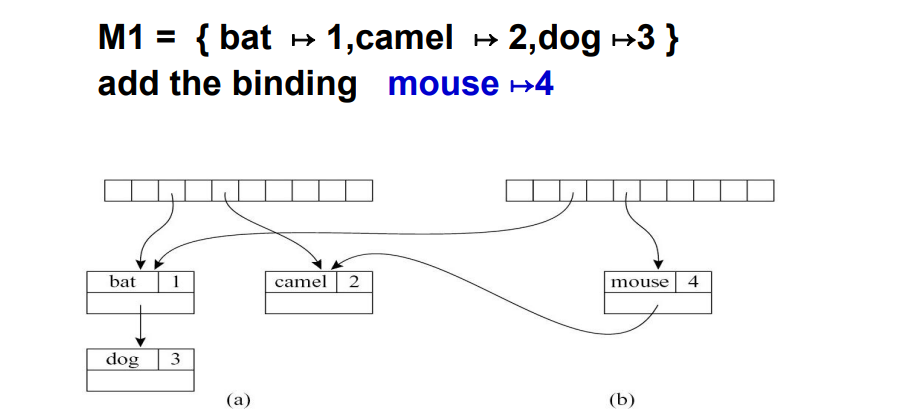
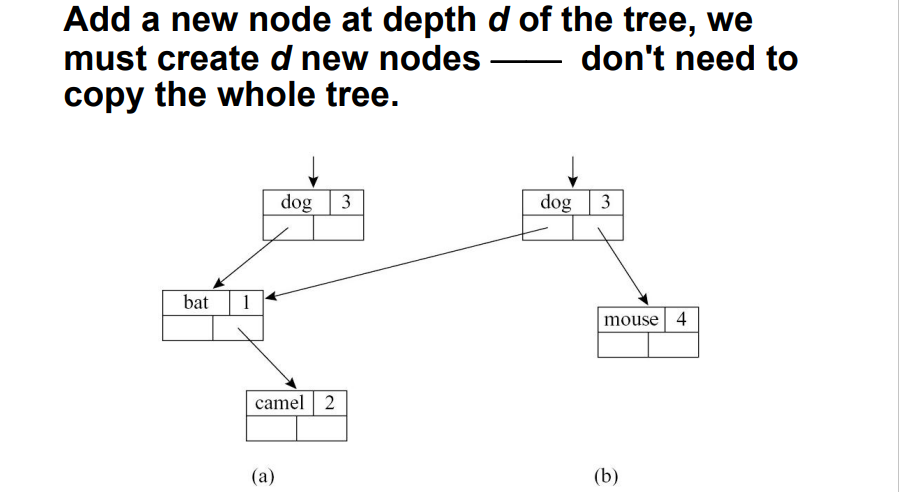
5.1.4 函数式符号表

  1. 当计算σ' = σ + {a ↦ τ}时，我们只需要让σ'的指针指向σ的bucket即可
  2. 删除时，直接释放σ'中的指针

image-20230327114249094

image-20230327114315245

5.1.5 Tiger编译器中的符号表

image-20230327114550222

image-20230327114731418

image-20230327114806188

image-20230327114920302

5.1.6 范围规则和块结构 Scope rules and block structure

两个规则：

  1. 先定义，后使用
  2. 就近匹配原则

具体要求：

  1. 在分析时，就需要构建符号表
  2. lookup时，选择尽可能近的符号定义
  3. 当lookup失败时：发生声明前使用变量的错误情况，编译器将发出适当的错误消息

5.2 Tiger编译器的绑定

类型等价：

  1. 结构等价 structure equivalence：两个结构体包含的成员变量的类型、数量是相同的
  2. 命名等价 name equivalence：两个结构体完全相同
  3. 声明等价 declare equivalence：声明过两个结构体相同

5.2.1 环境

Tiger语言的编译器，将环境分为Type environment、Value environment

image-20230403101725679

image-20230403101715253

5.3 Type-checking Expression

image-20230403101953632

type-checker是抽象语法树的一个递归函数：transExp

image-20230403102108865

变量转换：transVar

image-20230403102405598

5.4 Type-checking Declaration

5.4.1 变量声明

当出现声明语句时，Environment会发生改变

image-20230403102910846

image-20230403102751733

image-20230403103054061

5.4.2 类型声明

image-20230403103236744

5.4.3 函数声明

image-20230403103557588

5.4.4 递归声明

image-20230403104008862

image-20230403104029522

六、活动记录

活动记录和函数调用相关

  1. 函数的嵌套调用：使用栈传递函数的参数

    image-20230403104609213

  2. 函数的嵌套定义：子函数

    1. C语言不允许函数的嵌套定义
    2. 子函数可以调用父函数的变量：non-local and non-global

    image-20230403104618982

6.1 栈帧

  1. 栈指针：指向某个位置
    1. 堆栈通常只在函数的入口处增长，增量足够大，可以容纳该函数的所有局部变量
    2. 并且在函数退出之前保存这些变量
  2. 函数的活动记录/栈帧：
    1. 在栈中的一块空间，保存当前函数的局部变量、参数、返回值、临时变量
    2. 局部变量：用户定义的变量
    3. 临时变量：编译器在处理复杂表达式时产生的变量
    4. 保存寄存器：之前帧已经用到的寄存器
  3. Run-time stack通常从高地址开始，向低地址增长
    1. 堆通常是从低地址开始，向高地址增长
    2. 尽可能共用中间部分的代码

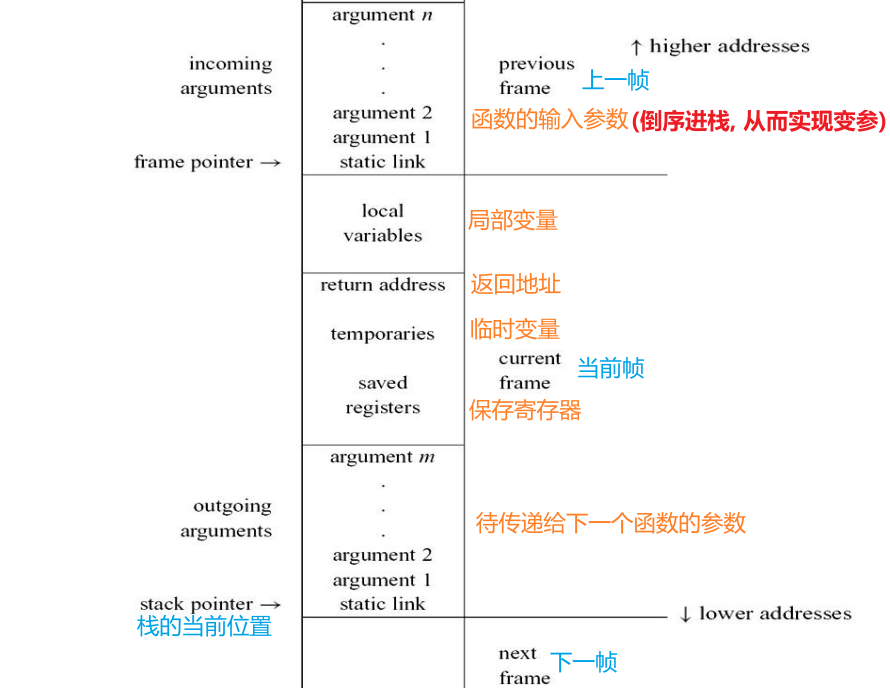
image-20230403112103765

6.1.1 栈帧的各个部分

caller：发起调用者

callee：被调用者

  1. 输入参数：caller压栈
  2. 返回地址：由call指令创建，通常为当前地址+1
  3. 局部变量、临时变量：callee压栈，可能有的变量放入了寄存器中
  4. 输出参数：传递参数
  5. static link：如果函数允许嵌套定义，则使用static link访问non-local-non-global变量

6.1.2 帧指针

  1. 当g调用f时：
    1. g压入参数，栈指针指向第一个参数的地址
    2. f申请一些栈空间，减小SP的值
  2. 当进入f时：
    1. 旧的FP保存到栈中
    2. 新的FP赋值为旧的SP
  3. 当退出f时：
    1. 将SP赋值为FP
    2. 从栈中读取FP的值

6.1.3 寄存器

设f和g均使用了寄存器r，g调用f

  1. 如果r是caller-saved register，则由g保存寄存器
  2. 如果r是callee-saved register，则由f保存寄存器

6.1.4 参数传递

四种传递类型

  1. value 值传递：C只有值传递
  2. reference 引用传递：只传地址，C可以通过传地址模拟该操作
  3. value-result 双向值传递：函数执行结束后，callee会向caller发起值传递
  4. name 名字传递：只有用到变量是，才发生传递

编译器可以选择将前k个参数放入寄存器

  1. 通常k=4/6

设函数f(a1, ... , an)调用了函数h(z)

  1. leaf procedures：不调用其他函数的函数
    1. 叶子函数不需要将他们的输入参数写入内存
  2. interprocedural register allocation
  3. dead variable：发生函数调用以后，变量不再使用
    1. 则函数可以直接使用该变量对应的寄存器，而不用保存

image-20230403114151248

image-20230403114217292

6.1.5 返回地址

image-20230403114236390

6.1.6 放在Frame中的变量

  1. 放在寄存器中的变量：
    1. 参数、返回值、返回结果
  2. 必须写入内存的原因：
    1. 当前变量通过引用传递
    2. 当前变量会被嵌套在该函数中的函数使用
    3. 当前变量的值太大，寄存器存不下
    4. 当前变量是一个数组，因为需要通过下标计算地址访问
    5. 寄存器保存的变量需要被用于一个特定用途，如参数传递
    6. 寄存器不够用了

在某些语言中，内部的函数会使用外部的函数，这种特性被称为block structure

  1. static link：当f被调用时，会传递一个指针，指向调用f的函数的栈帧
  2. display表：维护函数调用的层次关系
  3. lambda lifting：当g调用f时，f（或嵌套在f中的任何函数）实际访问的g的每个变量都作为额外的参数传递给f

image-20230403115642643

image-20230403115651944

6.2 Tiger编译器中的Frame

escape变量必须在内存中

image-20230403120825953

抽象层次：

image-20230403121309546

静态链接管理：

image-20230403121351400

七、翻译为中间代码

IR：Intermediate Representation，中间代码

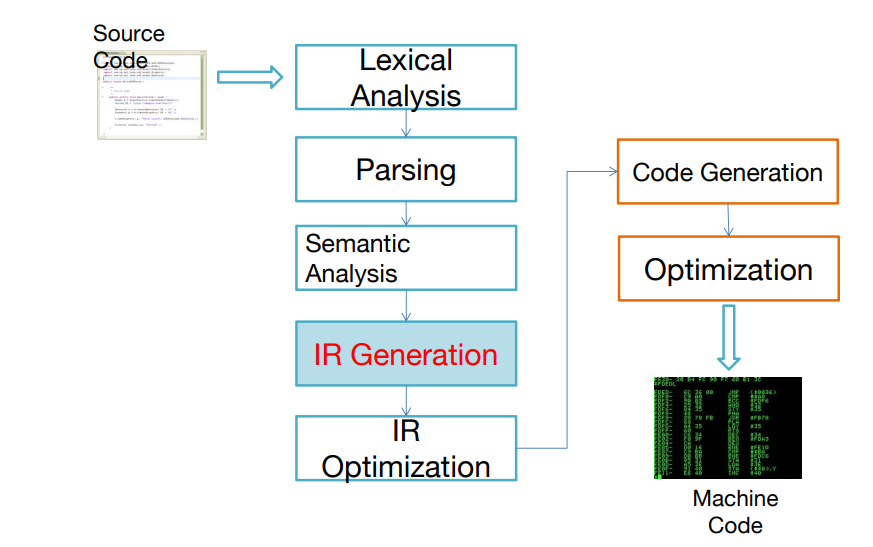
image-20230410100825954

什么是中间代码

  1. 中间代码是一种抽象机器语言
  2. 特性：
    1. 便于语义处理之后的生成
    2. 便于翻译为机器语言
    3. 便于优化

三地址码

  1. 每条语句最多有三个地址

    如 x = y op z，给定表达式2*a+(b-3)，会将其转换为：

    1. T1 = 2 * a
    2. T2 = b - 3
    3. T3 = T1 + T2

  2. 一条语句有四个元素：(四元组 quadruple)

    1. 一个表示operation
    2. 三个表示address，可为空

7.1 中间表示树

7.1.1 表达式T_exp

image-20230410103913293

7.1.2 语句T_stm

image-20230410104258077

7.2 翻译为树

7.2.1 表达式的结构定义

  1. 有返回值的表达式：T_exp
  2. 没有返回值的表达式：T_stm
typedef struct Tr_exp_ *Tr_exp;
struct Cx { 
    patchList trues;  // true时的标签
    patchList falses; // false时的标签
    T_stm stm;
};
struct Tr_exp_{ 
    enum { Tr_exp,Tr_nx,Tr_cx } kind;
    union { 
        T_exp ex; 	// 表达式
        T_stm nx; 	// 语句
        struct Cx cx; // 包含的内容
    } u;
};
static Tr_exp Tr_Ex ( T_exp ex);
static Tr_exp Tr_Nx ( T_exp nx);
static Tr_exp Tr_Cx ( patchList trues, patchList falses,T_stm stm);

a > b | c < d翻译为：

Temp_label z = Temp_newlabel();	// 申请临时标签
T_stm s1 = T_Seq(
    T_Cjump(T_gt, a, b, NULLt, z),	// a>b语句, 为真时跳到NULLt处(待后续补充), 为假时跳转到z处
    T_Seq (T_Label (z), 
           T_Cjump (T_lt,c,d, NULLt, NULLf))); // c<d语句, 为真时跳到NULLt处(待后续补充), 为假时跳转到NULLf处(待后续补充)

true和false的目标并不知道在哪里，但可以后续补充

typedef struct patchList_ *patchList;
struct patchList_ { 
    Temp_label *head; 
    patchList tail; 
};
static patchList PatchList(Temp_label *head, patchList tail);
patchList trues = PatchList(
    &s1->u.SEQ.left-> u.CJUMP.true,
    PatchList(&s1->u.SEQ.right->u.SEQ.right->u.CJUMP.true, NULL));
patchList falses = PatchList(
    &s1->u.SEQ.right->u.SEQ.right->U.CJUMP.false, NULL);
Tr_exp e1 = Tr_Cx (trues, falses, s1);

  1. 将一个表达式转换为等价的另一种表达式

    如 flag := (a>b | c<d)

  2. 三种类型转换函数

    static T_exp unEx(Tr_exp e);		// 表达式
    static T_stm unNx(Tr_exp e);		// 语句
    static struct Cx unCx(Tr_exp e);	// 条件语句

    如上述语句转换为：

    e = Tr_Cx (trues, falses, stm)
    MOVE (TEMP_flag, unEx(e))
static T_exp unEx(Tr_exp e) {
    switch (e->kind) {
        // 表达式
    	case Tr_ex:
    		return e->u.ex;
        // 条件语句
    	case Tr_cx: {
            Temp_temp r= Temp_newtemp(); // 申请临时变量
            Temp_label t = Temp_newlabel(), f= Temp_newlabel(); // 申请临时标签
            doPatch(e->u.cx.trues, t);
            doPatch(e->u.cx.falses, f);
            return T_Eseq(T_Move(T_Temp(r),T_Const(1)), // 临时变量r赋值为1
            			T_Eseq(e->u.cx.stm,  //
                        T_Eseq(T_Label(f), 
            			T_Eseq(T_Move(T_Temp(r),T_Const(0)),// 将r赋值为0
            			T_Eseq(T_Label(t), T_Temp(r))))));  // 运算结果为r
        }
        // 语句
        case Tr_nx:
    		return T_Eseq(e->u.nx, T_Const(0));
    }
    assert(0);
}

image-20230410105840570

// 将标签放入标签列表
void doPatch (patchList tList, Temp_label label) {
    for (; tList; tList = tList->tail)
    	*(tList->head) = label;
}
// 把两个列表连在一起
PatchList joinPatch (patchList first, patchList second) {
    if (!first) return second;
    for (; first->tail; first = first->tail);
    first->tail = second;
    return first;
}

7.2.2 简单变量

  1. 声明在当前活动记录栈帧中

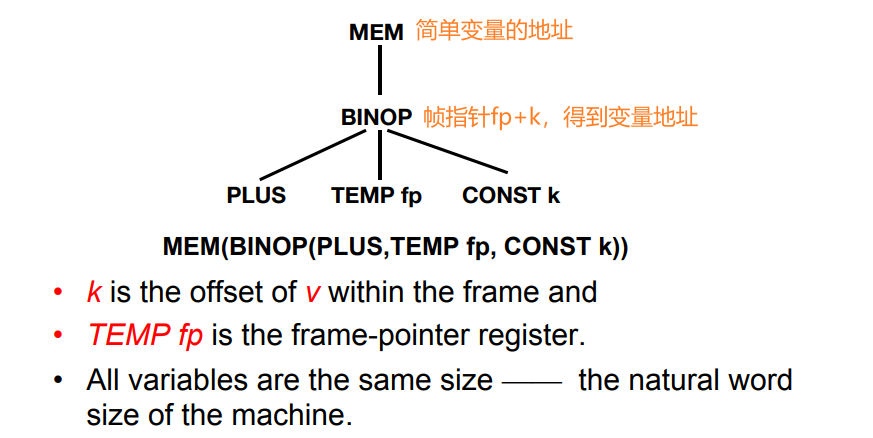
    image-20230410111417606

  2. 在Semant和Translate之间的接口

    image-20230410111746902

  3. 使用+(e1, e2)代替BINOP(PLUE, e1, e2)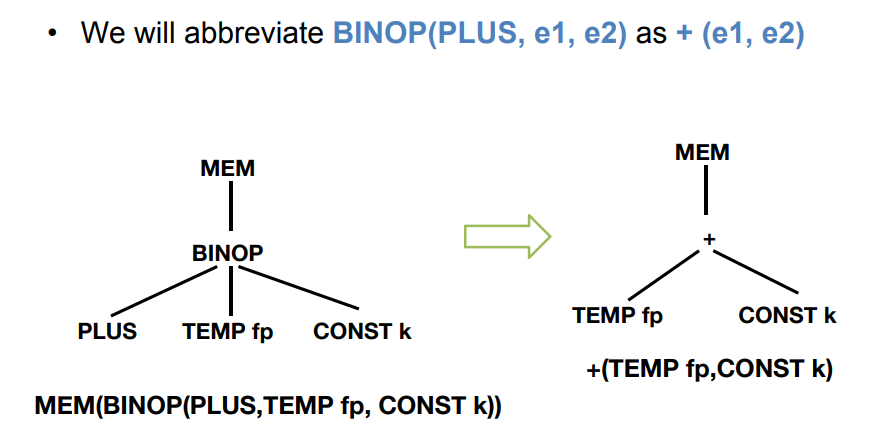

    image-20230410111705506

  4. 函数F_Exp

    image-20230410111917539

7.2.4 数组变量

Pascal中两个数组的赋值操作：

var a,b : array[1..12] of integer
begin
	a:=b
end;

C语言：

{ 
    int a[12], *b;
    b=a;
}

Tiger、Java、ML语言：数组变量的行为类似于指针操作

  1. 没有C中的数组名常量
  2. 新建数组的操作：ta[n] of i
    1. ta：数组类型的名称
    2. n：元素个数
    3. i：每个元素的初始值
let
    type intArray = array of int
    var a:= intArray[12] of 0
    var b:= intArray[12] of 7
in a:= b	// a指向了b, 原来的12个0就无法访问了
end

7.2.5 结构化左值

  1. 右值：表达式的右边
  2. 左值：表达式的左边
  3. 左值可以转换为右值，但右值不能转换为左值

image-20230410112634010

  1. 一个整数/指针，称为标量scalar：只包含一个元素

    1. Tiger中的所有左值均为标量

    image-20230410112805166

7.2.6 Subscripting and Field Selection

  1. 数组变量a是左值，a[i]也是

    1. 从a计算左值a[i]，需要进行地址运算

  2. a[i]的IR树：

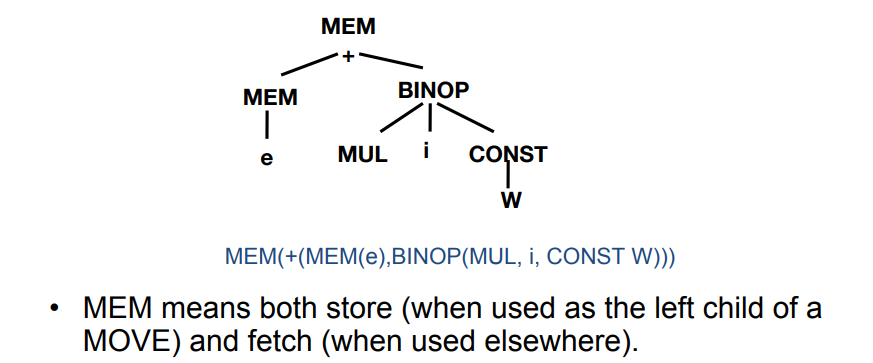
    image-20230410113043464

7.2.8 算术运算 Arithmetic

  1. 树语言不能表示单目运算

image-20230410113151479

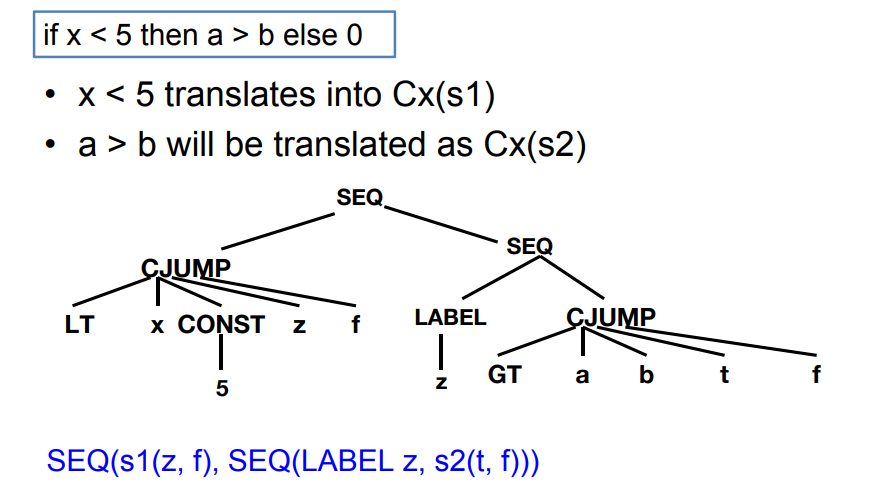
7.2.9 条件表达式 Conditionals

image-20230410113414602

示例：

image-20230410113525054

7.2.12 while循环语句

test:
	if not(condition) goto done
	body
	goto test
done
  1. break语句：
    1. 如果没有嵌套循环，则直接翻译为goto done
    2. 如果有嵌套循环，则需要有一个标签，作为break跳转的地方

7.2.13 For循环语句

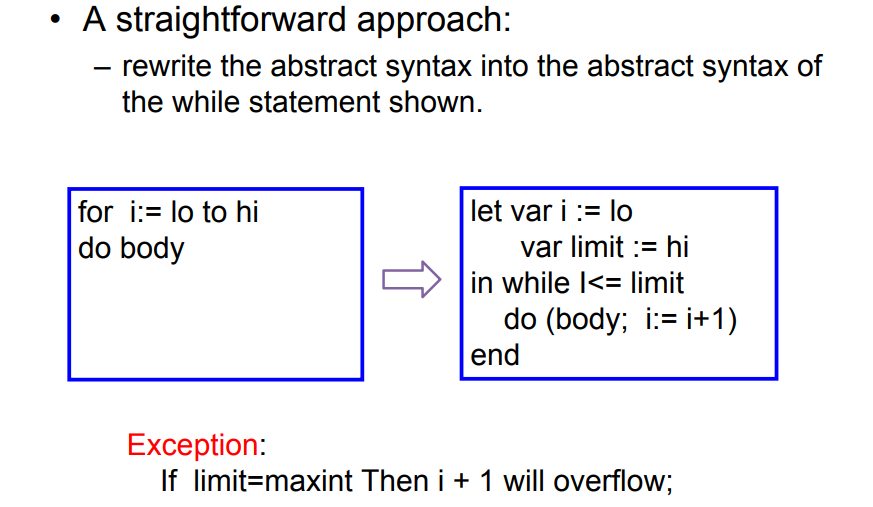
image-20230410113850656

7.2.14 函数调用CALL

  1. 要将static link也作为参数传递进去

image-20230410113931284

7.3 定义 Declaration

  1. 变量定义：
    1. 保存在frame中
  2. 函数定义：
    1. 在Tree Code中会新增一个fragment，用于保存函数体的代码

7.3.1 变量定义

image-20230410114200185

7.3.2 函数定义

函数会被转化成：

  1. prologue
    1. 伪指令：标记函数的开头
    2. label：表示函数名
    3. 指令：调整栈指针
    4. 指令：将escape参数放入frame，nonescape放入寄存器中
    5. store指令：保存callee-saved registers，包含return address register
  2. body
  3. epilogue
    1. 指令：将返回值保存到register中
    2. load指令：恢复callee-saved registers
    3. 指令：恢复栈指针
    4. return指令
    5. 伪指令：声明函数结束

7.3.3 Fragment

image-20230410114615061

/* frame.h */
typedef struct F_frag_ * F_frag;
struct F_frag_ { 
    enum {F_stringFrag, F_procFrag} kind;
    union {
        struct {
            Temp_label label;
        	string str;
        } stringg;
        struct {
            T_stm body; 
            F_frame frame;
        } proc;
    } u；
}；
F_frag F_StringFrag(Temp_label label, string str);
F_frag F_ProcFrag(T_stm body, F_frame frame);
typedef struct F_fragList_ *F_fragList;
struct F_fragList_ {F_frag head; F_fragList tail;};
F_fragList F_FragList(F_frag head, F_fragList tail);
/* translate.h */
void Tr_procEntryExit(Tr_level level, Tr_exp body, Tr_accessList formals);
F_fragList Tr_getResult(void);

八、基本块和轨迹

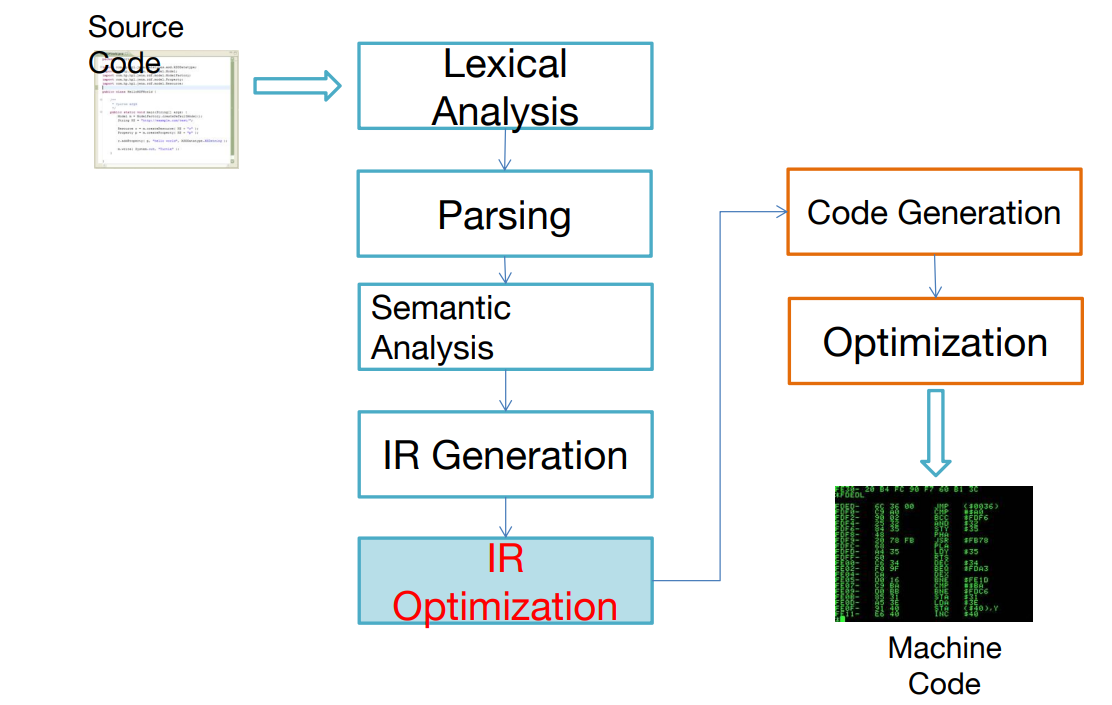
image-20230417191225375

8.0 Overview

现在生成的Tree Language与目标代码生成之间有一定的冲突

  1. CJUMP(op, exp1, exp2, true_label, false_label)：条件分支跳转
    1. 但是在机器码中，一条是默认分支，一条是要跳转的分支
  2. ESEQ(stmt, exp)：表达式序列，结果是exp的值
    1. 执行顺序会导致不同的结果
  3. CALL(f, list)：调用函数
    1. 在调用语句中含有表达式，如果表达式中含有其他节点的值，则会存在一定的问题

需要修改树的形态，使之避免上述问题

  1. 没有SEQ、ESEQ节点
  2. 可以划分为一组basic blocks，每个basic blocks之内没有跳转/标签
  3. 每个basic blocks按照顺序排列，形成traces的集合，其中每一个CJUMP之后均为其取false时的跳转目标

8.1 Canonical Trees

特点：

  1. 没有SEQ和ESEQ
  2. 每个CALL的父节点只能是EXP(...)或者MOVE(TEMP t, ...)

8.1.1 ESEQ的转换

思想：将ESEQ往上提，直到其变为SEQ

8.1.1.1 示例

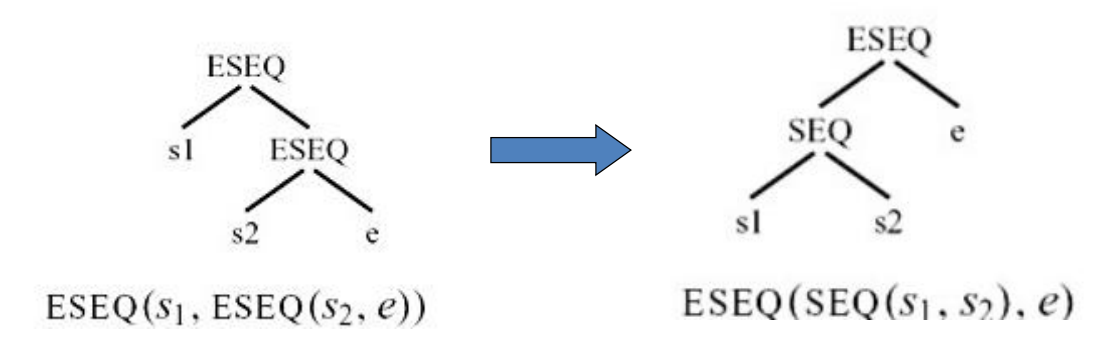
image-20230417213623702

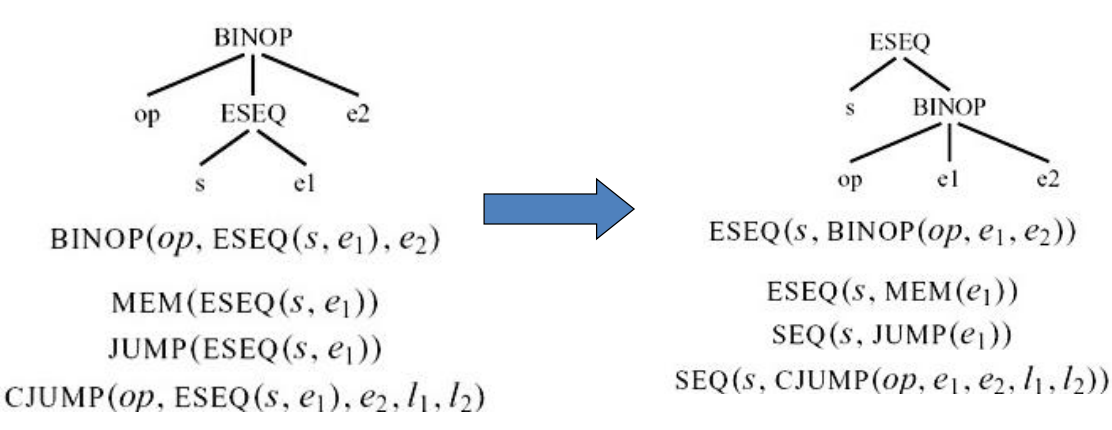
image-20230417213745729

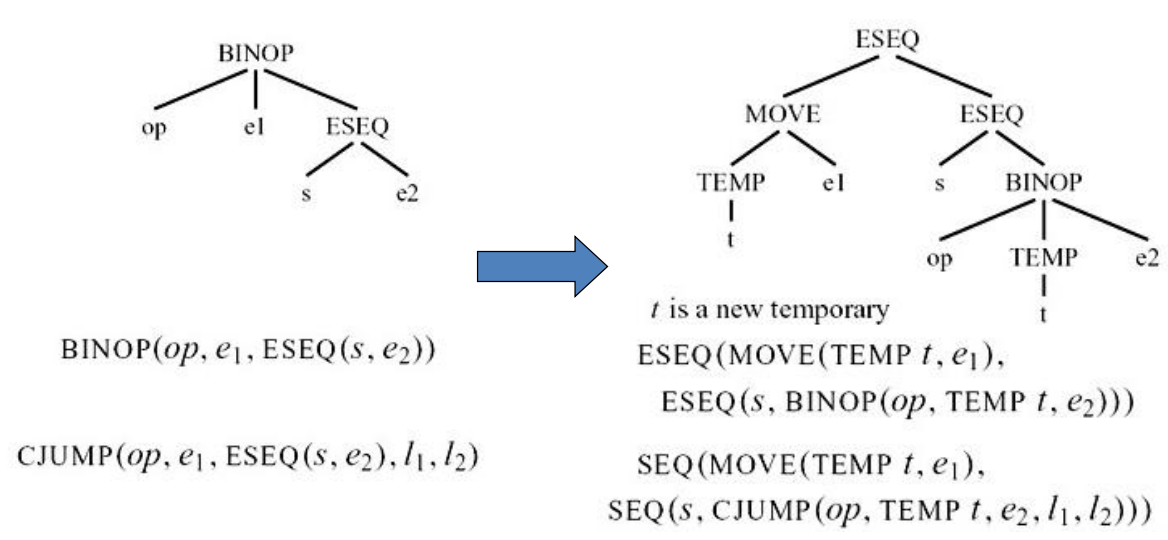
image-20230417213950404

image-20230417214501569

8.1.1.2 commute：判断一条语句和一个表达式能否交换

  1. exp为常量时，可以与任意语句交换
  2. statement是空语句时，可以与任意exp交换
  3. 其他情况均不可交换

image-20230417214601568

8.1.1.3 改写规则的方法

image-20230417214903599

8.1.1.4 算法

image-20230417215018122

reorder函数

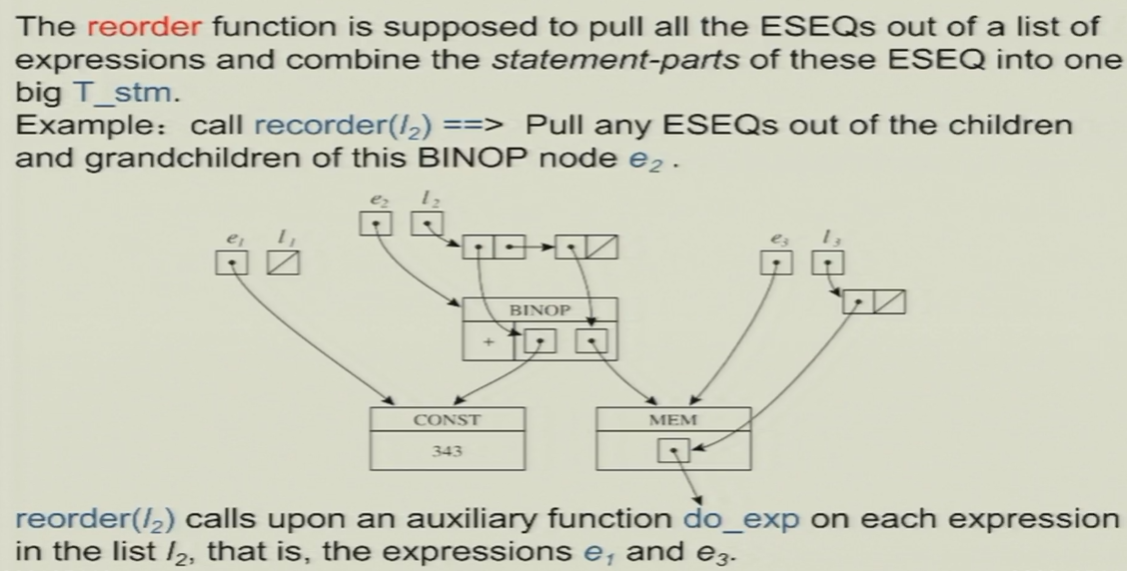
image-20230417215204624

image-20230417215401514

image-20230417215410650

image-20230417215706135

8.1.2 将CALL提升到最高层

对于BINOP(PLUS, CALL(), CALL())

  1. CALL的结果会放到一个特定的寄存器中
  2. 而第二次CALL会将第一次CALL的结果覆盖

因此，我们的需要：

  1. 将CALL的结果放到一个临时变量中
  2. 即将CALL(fun, args)转化为ESEQ(MOVE(TEMP t, CALL(fun, args)), TEMP t)

8.1.3 语句的线性链表

  1. 首先，SEQ(SEQ(a,b) c)与SEQ(a, SEQ(b, c)等价
  2. 因此，我们可以将其转化为一个语句的链表s1, s2, s3 ... sn，每个si中均不含SEQ或ESEQ节点

image-20230417220318817

8.2 条件分支的转换

  1. 将Canonical Tree转化为Basic Block
  2. 将Basic Block按照顺序转化为trace

8.2.1 Basic Block

一个Basic Block是一个语句的序列：始终在开头处进入，在结尾处退出，即

  1. 第一条语句是LABEL
  2. 最后一条语句是JUMP、CJUMP
  3. 基本块之间没有其他LABEL、JUMP、CJUMP

8.2.2 算法

  1. 从头到尾扫描语句序列
  2. 如果发现一个LABEL，则创建一个新的block，之前的block结束
  3. 如果发现一个JUMP、CJUMP，则之前的block结束，下一个block开始
  4. 如果离开了一个block，但是这个block不已JUMP、CJUMP结尾，则在该block结尾添加一个JUMP，跳转至下一个block
  5. 如果一个block没有以LABEL开头，则添加一个新的LABEL

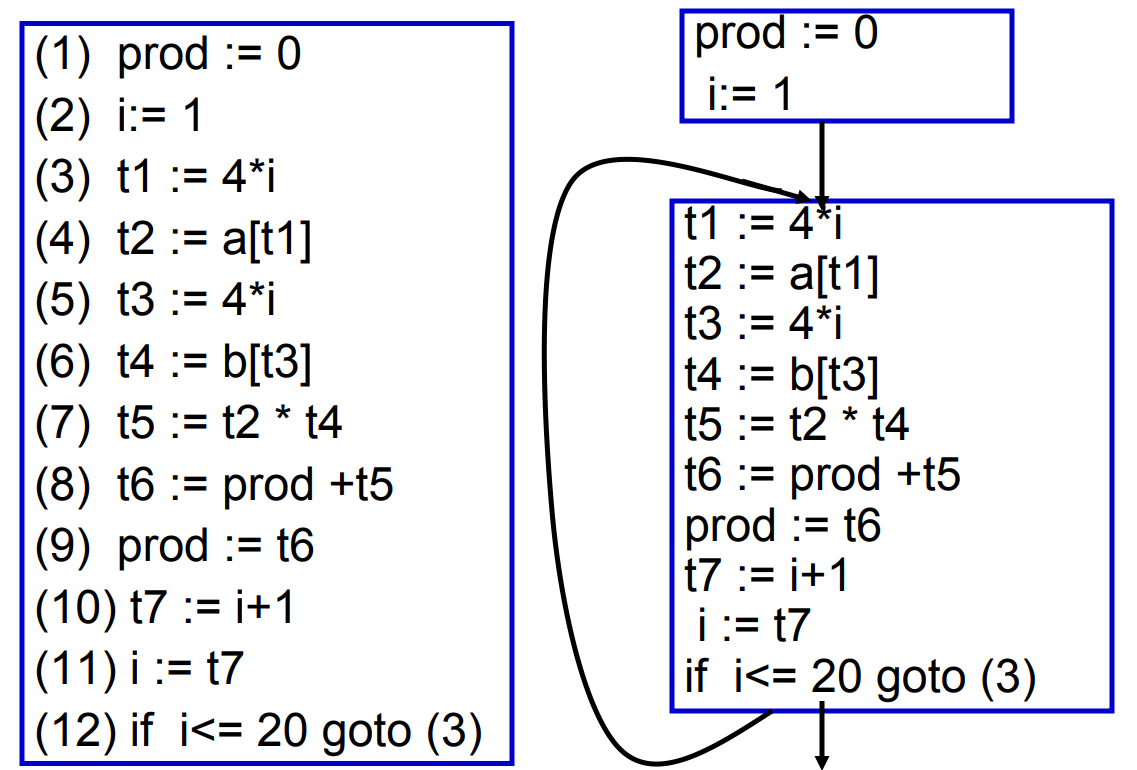
image-20230417221606433

8.3 Traces

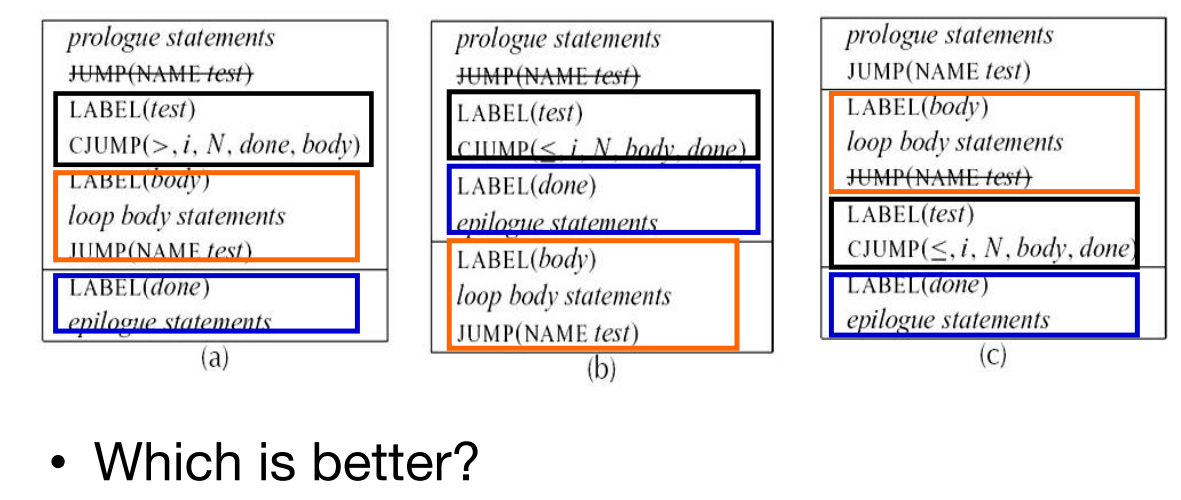
Basic Block可以按任何顺序排列，执行程序的结果将是相同的

  1. 我们可以利用这一点来选择一种顺序，满足：每个CJUMP后面跟着它的False_Label的块
  2. 我们还可以安排，每个JUMP后面紧跟着它们的目标Label。这将允许删除这些跳转，这将使编译后的程序运行得更快

Trace：

  1. Trace是在程序执行过程中可以连续执行的一系列语句。它可以包括条件分支
  2. 我们想要制作一组包含整个程序的Traces：每个Block必须正好在一个Trace中
  3. 我们希望在我们的covering set中有尽可能少的Trace

8.3.1 算法

思想：从一些block开始，沿着某一条可能的执行路径，到达trace的终点

设b1→b4→b6，则这个trace为：b1, b4, b6

设b6的结尾为条件跳转CJUMP(cond, b7, b3)，则将b3添加进trace中，b7会进入其他的trace

算法：

将程序的所有block添加进列表Q
while (Q不为空) {
	创建一个空的trace, 记为T
	删除Q中的第一个块b
	while (b没有被标记过) {
		标记b
		将b添加到T的结尾
		检查b执行结束之后可能会进入的块c
		if (c没有被标记){
			b ← c
		}
	}
	结束当前的trace
}

8.3.2 Finishing Up

将有序的trace列表展开为一个语句的列表

  1. 所有CJUMP后面为它的False_Label的，保留

  2. 所有CJUMP后面为它的True_Label的，将条件取反，并交换True_Label和False_Label

  3. 所有CJUMP(cond, a, b, It, If)后面为其他标签的，创建一个新的Fals_Label If'，重写CJUMP使得其后面为它的False_Label：

    CJUMP(cond, a, b, It, If_);
    LABEL If_;
    JUMP(NAME If);

8.4 优化 Trace

对于频繁执行的指令序列(如循环体)，应该具有自己的trace：

  1. 这有助于最小化JUMP的数目
  2. 且有助于其他类型的优化，如寄存器分配、指令调度

image-20230417224345490

C最好，因为可以删除 JUMP(NAME test) 这句话

九、指令选择

任务：将IR树转化为机器指令，暂时不考虑寄存器够不够的问题

Overview

9.0.1 Jouette architecture 指令集

  1. 寄存器r0始终为0
  2. TEMP节点也被视作一个寄存器
  3. 有些指令可能对应多个树模式

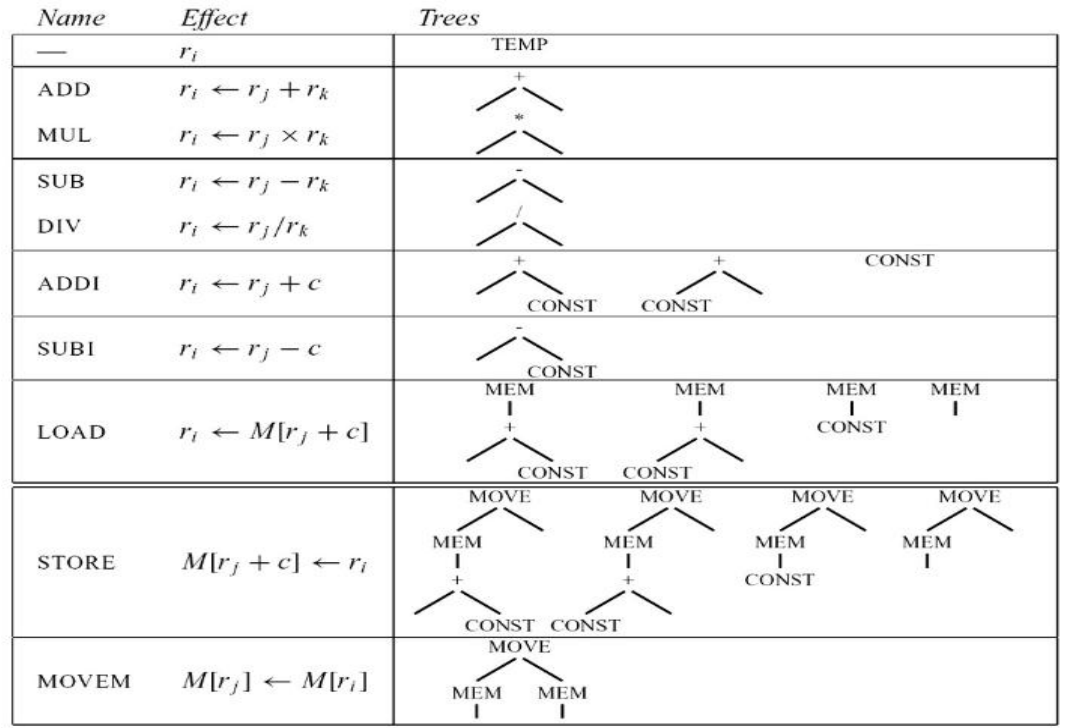
image-20230508100735256

9.0.2 将IR树转化为指令

  1. 基础思想：将已有的指令及其对应的树结构当作tile，用tile覆盖整个IR树
  2. 注意，覆盖的方式可能不同，且覆盖有先后顺序

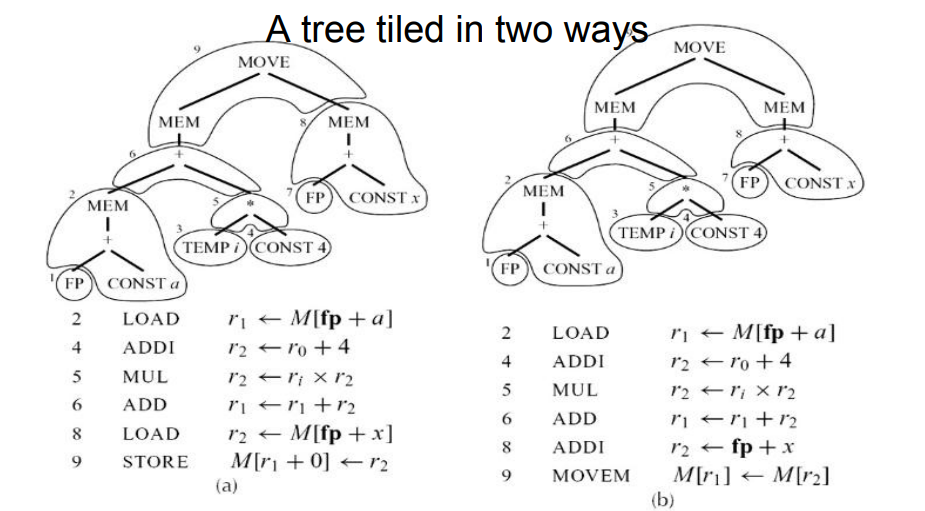
image-20230508102001642

9.0.3 最优覆盖

  1. 产生的指令序列最短
  2. 或者使用成本最低的序列，因为不同指令的指令周期不同

Optimal & Optimum tiling：

  1. Optimum tiling：最优解，得到成本最低的tile覆盖
  2. Optimal tiling：无法再优化的解，得到一个tile覆盖后，相邻的两个瓦片无法再合并为一个
  3. Optimum一定是Optimal，但Optimal不一定是Optimum

9.1 指令选择的算法

  1. 对于CISC指令集来说，Optimum和Optimal的区别较大，因为这种指令粒度较大
  2. 对于RISC指令集来说，Optimum和Optimal的区别不大

9.1.1 Maximal Munch算法

maximal munch主要思想：

  1. 从树的根开始，找到最大的能匹配的tile，覆盖掉根节点以及几个子节点
  2. 将覆盖过的节点删除，会将树划分为几个子树
  3. 对剩下的子树重新执行1操作，直到所有节点都被覆盖

算法解释：

  1. 生成指令的顺序为逆序
  2. 如果有两个同样大小的tile覆盖根节点，则随意选择一个
  3. 有两个函数：munchStm、munchExp

image-20230508104357860

image-20230508104411883

image-20230508104436671

9.1.2 动态规划算法

  1. 可以找到Optimum最优解
  2. 算法是自底向上的
  3. 每次选择最小cost的match

9.1.2.1 算法描述

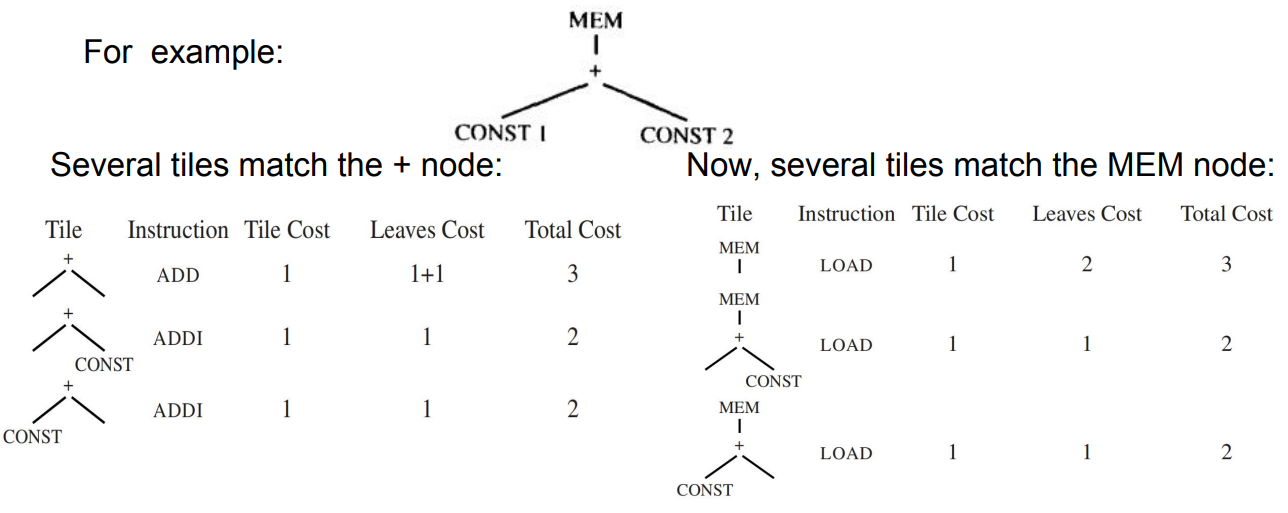
image-20230508104844190

一旦找到了根节点的cost，说明找到了整个树的cost，就会开始指令生成

  1. Emission(node n)：对于节点n选择的tile每个叶节点li，执行Emission(li)，然后再执行节点n的指令选择
  2. Emission(n)不会在节点n的子节点上递归，而是在节点n处匹配的tile树上递归

9.1.2.2 对指令集的进一步划分

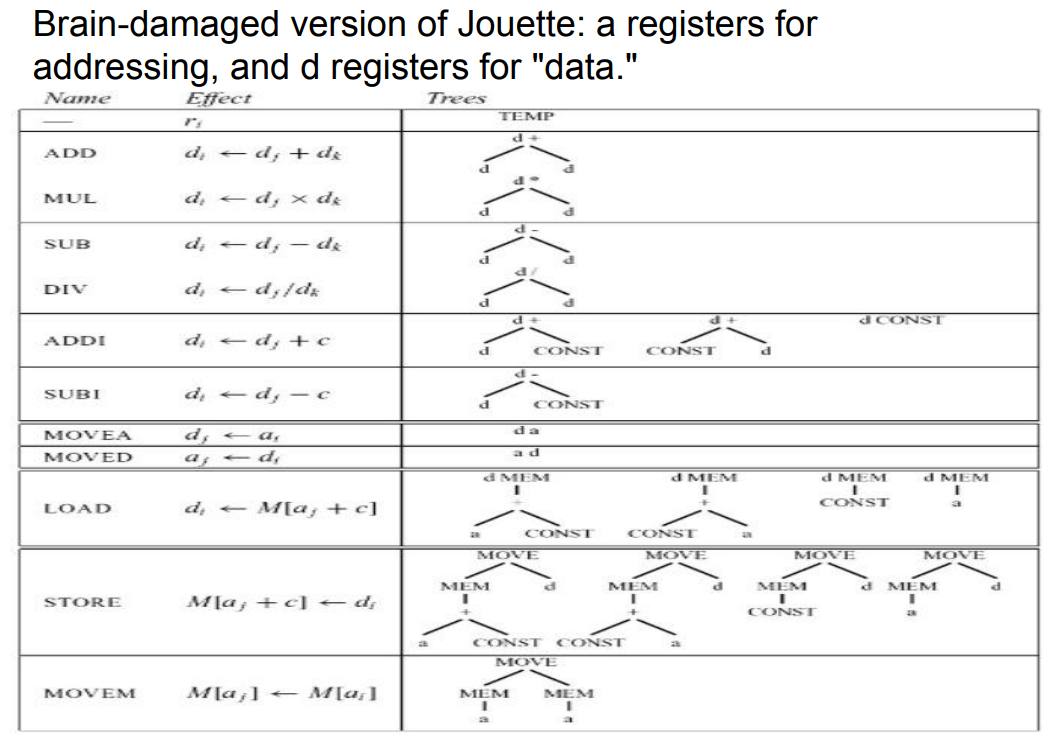
image-20230508105506270

使用CFG描述tiles：

  1. s：语句
  2. a：将表达式的值赋值给一个地址寄存器
  3. d：将表达式的值赋值给一个数据寄存器

image-20230508105649097

9.1.3 快速匹配

image-20230508105755975

9.1.4 Tiling算法的效率

image-20230508105836036

9.2 CISC指令

9.2.1 RISC指令集特点

image-20230508110855781

9.2.2 CISC指令集特点

image-20230508110911242

9.3 CISC的问题和解决方法

  1. 寄存器的分类：有些指令架构的指令要求特定寄存器才能使用

    1. 解决方法：将operand和result进行move

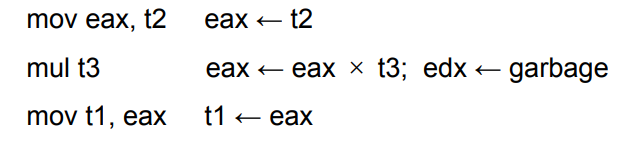
    image-20230508111346077

  2. 二地址指令

    1. 添加额外的指令

    image-20230508111412410

  3. 算术运算可能会访问内存：指令选择阶段将每个TEMP节点变成一个“寄存器”引用，这些“寄存器”中的许多实际上将成为内存位置

    1. 在操作之前将所有操作数取入寄存器，然后将其存储回内存

    image-20230508111648518

  4. 几种寻址模式：

    image-20230508111818397

  5. 可变长指令：

    image-20230508111825572

  6. 有边缘效应的指令：有些机器有一个“自动递增”内存提取指令，其效果是

    image-20230508111848319

十、活性分析

目的：判断每个变量的活性，影响最后的寄存器分配

如何做：控制流、从未来推出过去

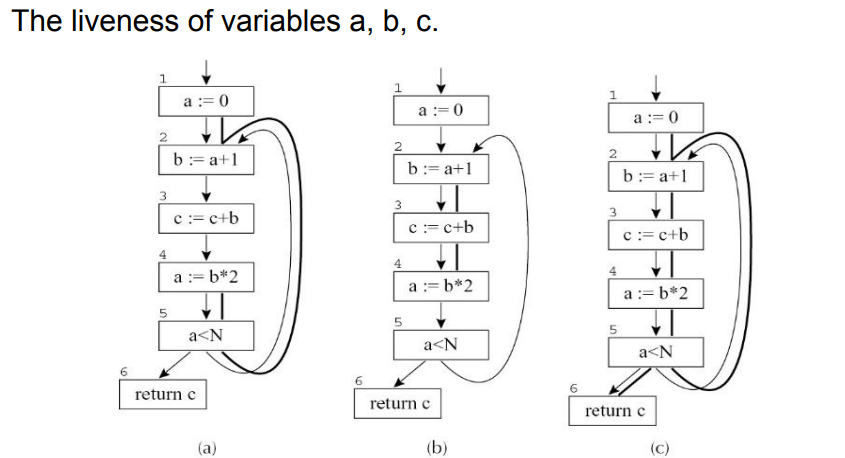
变量的活性：定义=>使用，整个过程必须是活的

粗线代表每个变量为liveness的周期

  1. 从下图可知，a和b不会同时为livenes，因此a和b可以使用同一个寄存器

image-20230515102016319

10.1 数据流方程的求解

10.1.1 相关定义

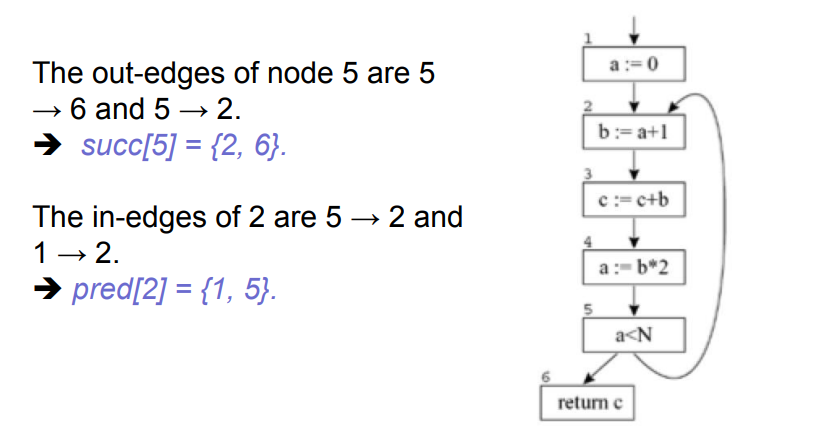
Flow-graph terminology：

  1. out-edge：指向后继节点的边，succ[n]表示当前节点的后继节点
  2. in-edge：从前序节点指向当前节点，pred[n]表示当前节点的前序节点

image-20230515102411421

Uses and defs：

  1. use：对变量的访问，即变量出现在赋值语句的右边，use[i]表示当前节点使用到的变量
  2. def：对变量的定义，即变量出现在赋值语句的左边，def[i]表示当前节点定义的变量

image-20230515102655658

Liveness：

  1. live-in：该变量在当前节点的in-edge上是活跃的
  2. live-out：该变量在当前节点的out-edge上是活跃的

10.1.2 计算Liveness

  1. 如果变量在use[n]中，则它是节点n的live-in
  2. 如果变量是节点n的live-in，则它是pred[n]中所有节点的live-out
  3. 如果变量是节点n的live-out，且不在def[n]中，则它是节点n的live-in

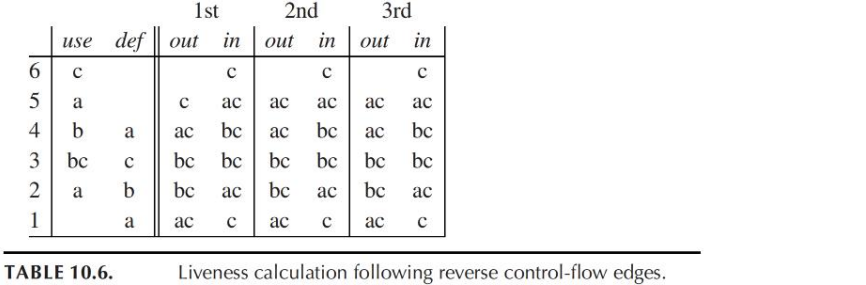
10.1.3 数据流方程

\[ \begin{aligned} in[n] &=use[n]\cup(out[n]-def[n])\\ out[n] &=\cup_{s\in succ[n]}in[s] \end{aligned} \]

image-20230515103250601

示例：

image-20230515103600986

image-20230515103550190

迭代次数多的原因：计算当前节点的out[n]时，需要先知道后继节点的in[n]

  1. 倒过来计算的过程

image-20230515104108315

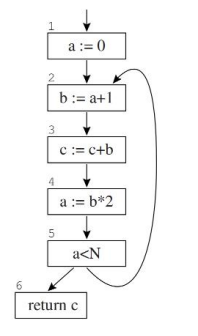
10.1.4 与基本块结合

  1. Basic Block内的每个节点，均只有1个前序节点，1个后继节点
  2. 可以将Basic Block看作一整个node，他们的in[]、out[]合并到一起

10.1.5 表示in、out集合

  1. bit-array：

    1. 设程序中有n个变量，则每个集合需要使用n-bit
    2. 计算两个set的并集，即将两个n-bit数做或运算

  2. Sorted List：

    1. 按照变量名排序，记录当前节点的in、out集合
    2. 计算两个set的并集，即将两个链表合并

  3. 计算的时间复杂度：

    image-20230515104644473

10.1.6 最小不动点 Least-Fixed-Point

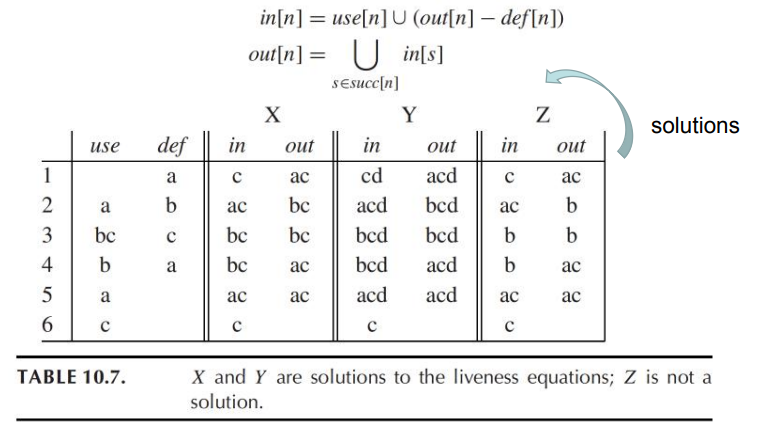
image-20230515104852113

  1. 上述算法是conservative approximation保守近似
  2. 在如上例子中，d是live-out的，但不意味着d一定会被用到

10.1.7 Static vs Dynamic Liveness

定理：不存在程序H(P, X)，返回如果P(X)可以停机就是true，否则为false

  1. P：任意一个程序
  2. X：P的输入

推论：不存在程序H'(P, L)，返回在P的计算中，L是否可以到达

  1. P：任意一个程序
  2. L：P中的一个label

Dynamic Liveness：

  1. 如果程序的某个执行从节点n到a的一个使用之间没有经过a的任何定义，那么变量a在节点n是动态活跃的

Static Liveness：

  1. 如果存在一条从节点n到a的某个使用的控制流路径，且此路径上没有a的任何定值，那么变量a在节点n是静态活跃的

如果a为动态活跃，则a也为静态活跃。因此编译器通常根据静态活跃信息来进行寄存器分配和其他优化

10.1.8 干涉图 Interference Graphs

  1. 设变量集合为{a, b, c, ...}，寄存器集合为{r1, ..., rk}
  2. 阻止将a和b分配到同一个寄存器的条件称为interference

interference的常见情况：

  1. 活性周期有重合
  2. 如果生成a的指令无法寻址寄存器r1，则a和r1也是interfere的

冲突信息可以用矩阵来表示，也可以用无向图来表示

image-20230515112000976

MOVE指令的特殊处理：

  1. 下列情况中，s和t的内容完全相同，因此不需要添加(s,t)的干涉边
  2. 当然，如果之后还有t的另一个定义，且该时刻s仍然是活跃的，则要创建(s,t)的干涉边

image-20230515110515633

因此，为每一个新定义的值添加冲突边的方法为：

  1. 对于任何定义变量a的非copy指令，以及在该指令处是live-out的变量{b1, ... bj}，添加干涉边(a, b1)，...，(a, bj)
  2. 对于copy指令a←c，以及在该指令处是live-out的变量{b1, ... bj}，对每一个不同于c的bi添加干涉边(a, b1)，...，(a, bj)

十一、寄存器分配

image-20230522100931468

寄存器分配的任务：

  1. 将大量的临时变量分配到少量寄存器中
  2. 在可能的情况下，给一条MOVE指令的源地址和目的地址分配同一个寄存器，以便能删除该MOVE指令
  3. 在干涉图上执行着色算法

11.1 通过简化进行着色

  1. 寄存器分配是一个NP-Complete问题
  2. 可以使用一个线性近似算法得到一个较优解

11.1.1 Build 构造

构造冲突图

  1. 利用数据流分析方法，计算在每隔程序点同时活跃的临时变量集合
  2. 由该集合中的每一对临时变量形成一条边。并将这些边加入冲突图中
  3. 对程序中的没一点重复这一过程

11.1.2 Simplify 简化

用一个简单的启发式方法，对图进行着色

  1. 设图\(G\)有一个节点\(m\)，它的相邻节点小于\(K\)个，\(K\)是实际寄存器的个数
  2. 令\(G'=G-\{m\}\)，如果\(G'\)能够使用\(K\)种颜色着色，那么\(G\)也可以
    1. 因为当将m添加到一着色的图\(G'\)时，\(m\)的相邻节点至多使用了\(K-1\)种颜色
    2. 所以总是能找到一种颜色作为\(m\)的颜色

这很自然的导出了一种递归(stack-based or recursive)的图着色算法：

  1. 重复删除\(degree <K\)的节点，并将其压入栈中
  2. 每简化掉一个节点，都会减少其他节点的度数，从而产生更多的简化机会

11.1.3 Spill 溢出

在简化过程的某一点，图\(G\)只包含\(degree\ge K\)的节点

  1. 在图中选择一个节点，并决定在程序执行期间，它存储在memory中
  2. 我们对这个溢出的效果做出乐观的估计，寄希望与这个被溢出的节点将来并不会与留在图中的其他节点发生冲突
  3. 因此可以将这个选中的节点从图中删除，并压入栈中，然后继续进行SImplify操作

11.1.4 Select 选择

将颜色指定给图中的节点

  1. 从一个空的图开始，重复的将栈顶结点添加到图中，重建原来的冲突图
  2. 根据简化阶段的定义，每次往图中添加一个节点时，一定会由一种它可以使用的颜色

当从栈中弹出一个用溢出启发式算法压入栈的潜在溢出节点\(n\)时，并不能保证它是可着色的

  1. 在图中，它的相邻节点可能已经使用了\(K\)中不同的颜色
  2. 在这种情况下，我们就会有一个实际溢出
  3. 此时，我们不知拍任何颜色，而是继续执行Select操作，来识别其他的实际溢出

但是，潜在溢出节点\(n\)的相邻节点，可能使用相同的颜色，导致总颜色种类数\(<K\)

  1. 此时，我们就可以给节点\(n\)着色，并且它不会称为一个实际溢出
  2. 这种方法被称为优化着色 optimisitic coloring

11.1.5 Start Over 重新开始

  1. 如果Select阶段不能为某些节点找到颜色，则必须对程序进行改写，使得在每次使用这些节点之前，将它们从memory中读出，在每次对这些节点赋值之后，将它存回memory中
  2. 这样，一个被溢出的临时变量就会转变为几个具有较小活跃范围的新的临时变量。这些新的临时变量可能会与图中的其它临时变量发生冲突，因此对改写后的程序还要重新进行一次寄存器分配。
  3. 这种处理过程反复迭代，直到没有溢出而简化成功为止

11.2 合并 Coalescing

如果一条MOVE指令对应的两个节点之间不存在边，则可以删除该MOVE指令，并且将两个节点合并为一个节点。

由于合并会导致节点的度数增加，从而可能使图无法进行K着色，因此存在两种合并策略：

11.2.1 合并策略

  1. Briggs：如果节点\(a\)和\(b\)合并产生的节点ab的高度数(\(\ge K\))相邻节点的个数少于\(K\)个，则节点\(a\)和\(b\)可以合并
  2. George：如果对于\(a\)的每一个邻居\(t\)，\(t\)要么与\(b\)有冲突，要么是低度数(\(<K\))的节点，则\(a\)和\(b\)可以合并

11.2.2 带有合并的着色算法

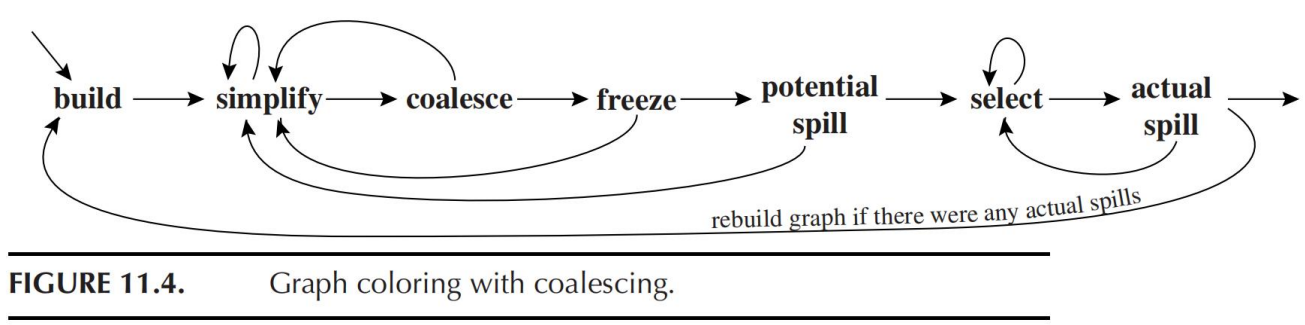
image-20230522105241793

  1. 构造：
    1. 构造冲突图
    2. 将每个节点分为move-related or non-move-related
      1. move-related：该节点是一条MOVE指令的操作数
  2. 简化：
    1. 每次从图中删除低度数的且传递无关的节点
  3. 合并：
    1. 对简化阶段得到的简化图，执行保守的合并
  4. 冻结：
    1. 如果Simplify和Coalesce均不能操作，则找到一个度数较低的传递有关的节点，冻结该节点，然后重新开始Simplify和Coalesce操作
    2. 冻结：放弃对该MOVE指令进行合并的希望，将该节点视为传递无关的
  5. 溢出：
    1. 如果没有低度数的节点，选择一个潜在可能溢出的高度数节点，并将其压入栈
  6. 选择：
    1. 弹出整个栈，并给每个节点着色

11.3 预着色的节点 Precolored Node

  1. 有一些临时变量是预着色的，它们代表的是机器寄存器
  2. 对于每一个由专门用途的真实寄存器，算法应该使用与这些寄存器永久绑定的特殊临时变量
  3. 对于任一给定颜色(机器寄存器)，应该只有一种使用这种颜色的预着色节点
  4. Select和Coalescing操作可以给普通临时变量分配与预着色寄存器相同的颜色，只要它们之间不发生冲突，即：
    1. 一个调用约定的标准寄存器能够在过程中重新用于临时变量
    2. 预着色节点可以通过保守合并算法，与其他非预着色节点合并
  5. 预着色节点有指定的颜色，且不能将其溢出到寄存器

11.3.1 机器寄存器的临时副本

着色算法通过不断执行Simplify、Coalescing、Spill操作，直到只剩下预着色节点，然后Select阶段才能开始向冲突图中加入其他节点，并且对它们进行着色

  1. 预着色节点不能被溢出，因此前端必须尽可能让它们的活跃范围较小
  2. 可以通过生成保存和恢复预着色节点值的MOVE指令来实现这一点

image-20230522115203138

11.3.2 caller-saved寄存器、calllee-saved寄存器

image-20230522115231125