GAMES104-06:渲染:地形、大气、云的渲染
六、渲染:地形、大气、云的渲染
6.1 地形的几何
6.1.1 Heightfield


6.1.3 两个优化的准则
- FOV越窄,三角形划分越密集

- 和ground truth在屏幕上的误差不要超过一个像素

6.1.4 基于三角形的剖分

T-Junctions
- 问题:当两个相邻的三角形在同一个边上,这个三角形没有切分这条边,而相邻三角形切分了(高度会随之变化),会导致地形上有个裂缝
- 解决方法:如果发现边上有邻居对相邻边的切分更密集,则当前三角形也需要将该边切分,直到与邻居的切分数相同
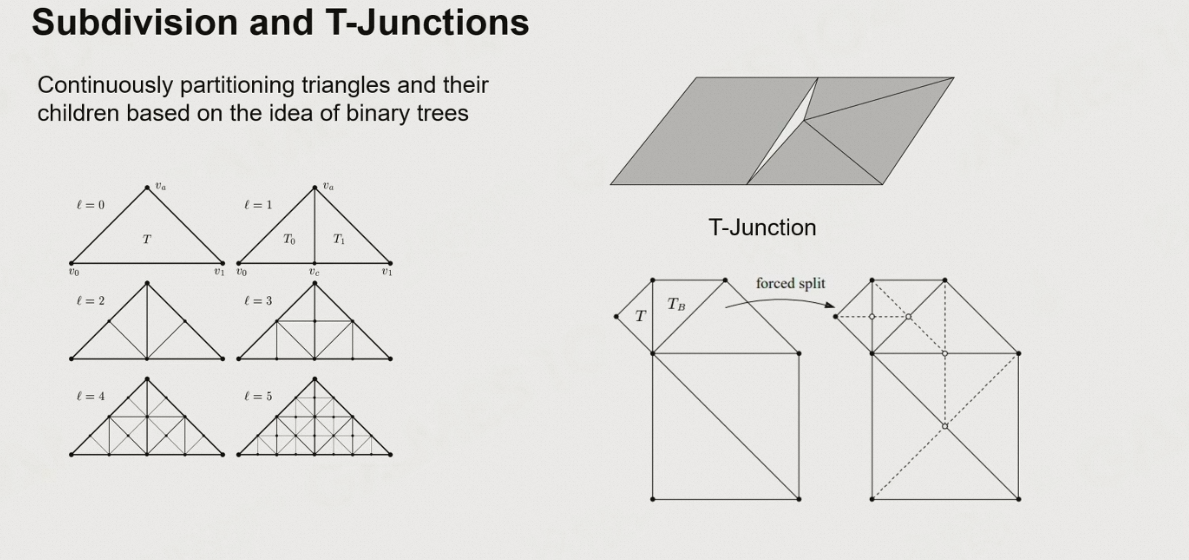
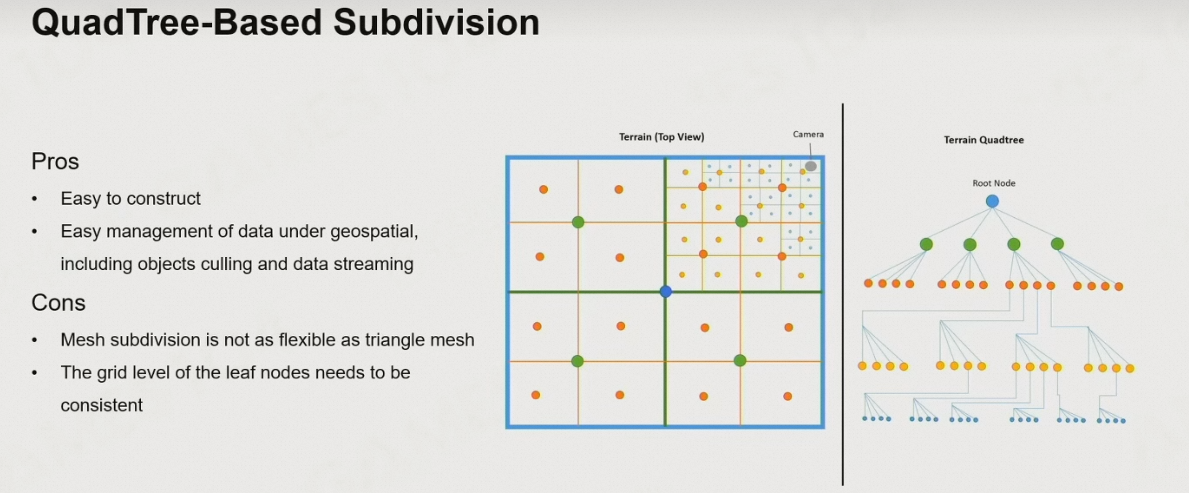
6.1.5 基于四叉树的切分

解决T-Junctions的问题:Stitching吸附
- 将划分更密集的那个三角形的中心,对齐到更稀疏的三角形上
- 即划分出了一个面积为0的三角形
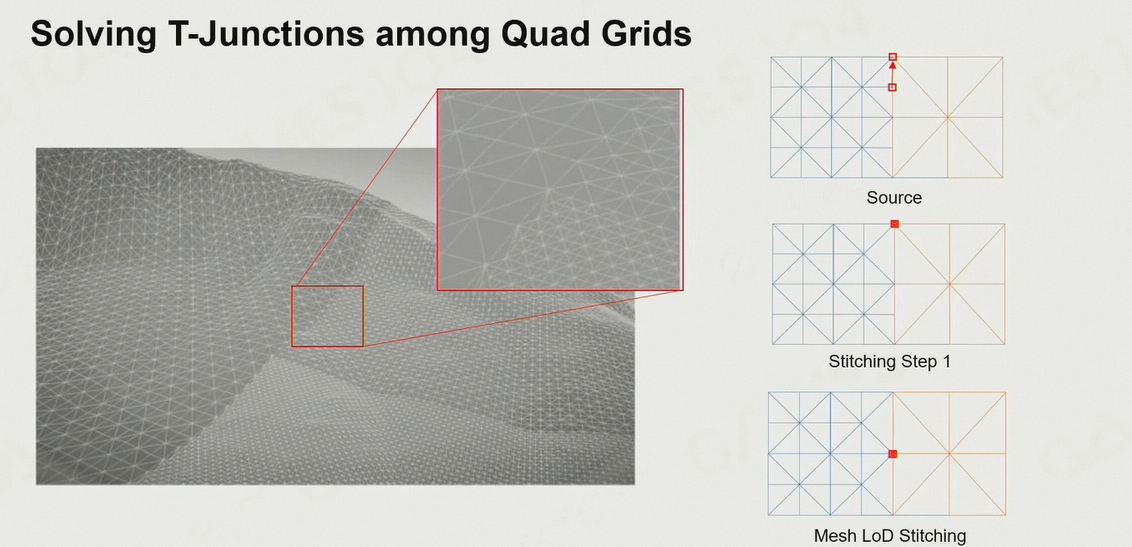
6.1.6 基于不规则三角形的绘制 TIN
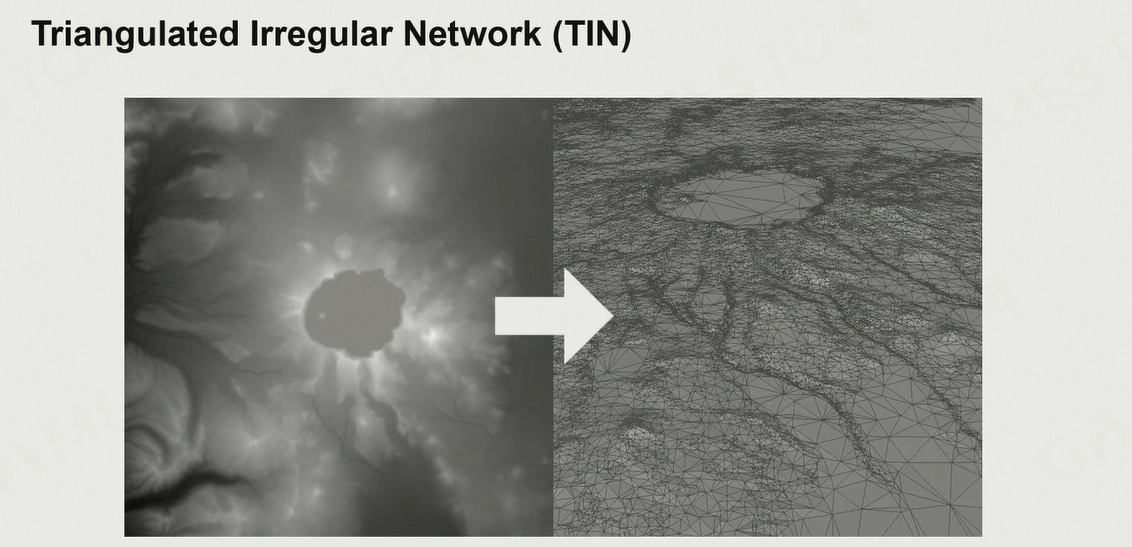
通过顶点简化,减少三角形的数目
优点:
- 通常情况下,三角形的数目更少
缺点:
- 地形的三角形难以在渲染的时候调整
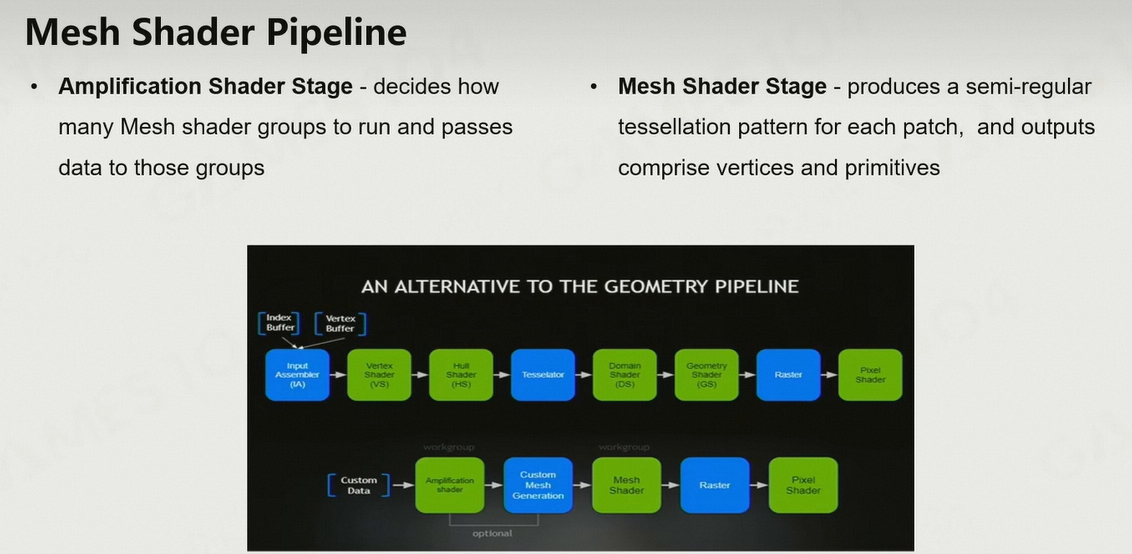
6.1.7 基于GPU的曲面细分(Tessellation)
DirectX12开始支持Mesh Shader
- 在给定Mesh Shader之后,Mesh Shader会生成一小块meshlit(一小片顶点&三角形),顶点&三角形如何插值、如何凸包由shader控制
6.1.8 Real-Time Deformable Terrain
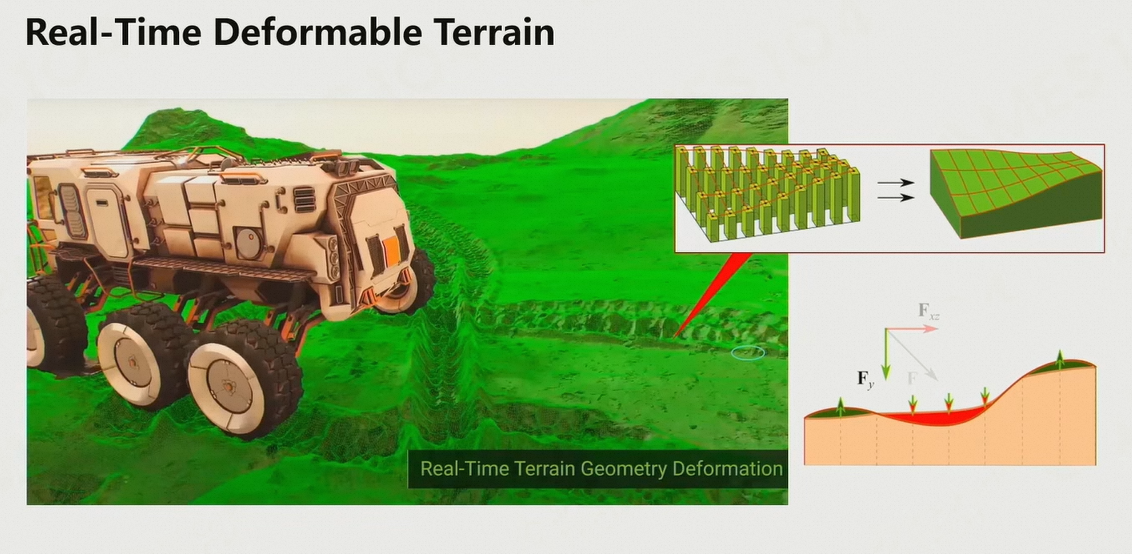
如果所有顶点的位置都可以在runtime动态调整,则可以让地形产生动态效果
- 在人物的周边生成一个terrain deformable的texture,将这上面的脚印记录在texture上
- 当移动的时候,texture跟着角色走,但是要保持数据一致性
- 由于地形数据是实时细分出来的,就可以根据texture添加一些offset
- 还要注意更新地形的碰撞
6.1.9 Non-Heightfield Terrain
地形不止有起伏,还有悬崖山洞之类的物体
6.1.9.1 在Terrain中开一个洞

- 可以在设置顶点位置的时候,判断一下这个顶点是否在洞中
- 如果在洞中,则将其位置设为NaN
- GPU在看到位置为NaN的顶点后,不会绘制用到这个顶点的所有物体
- 然后再通过加一个山洞的模型,避免地形上的zigzag条纹显示出来
6.1.9.2 地形体素化表达

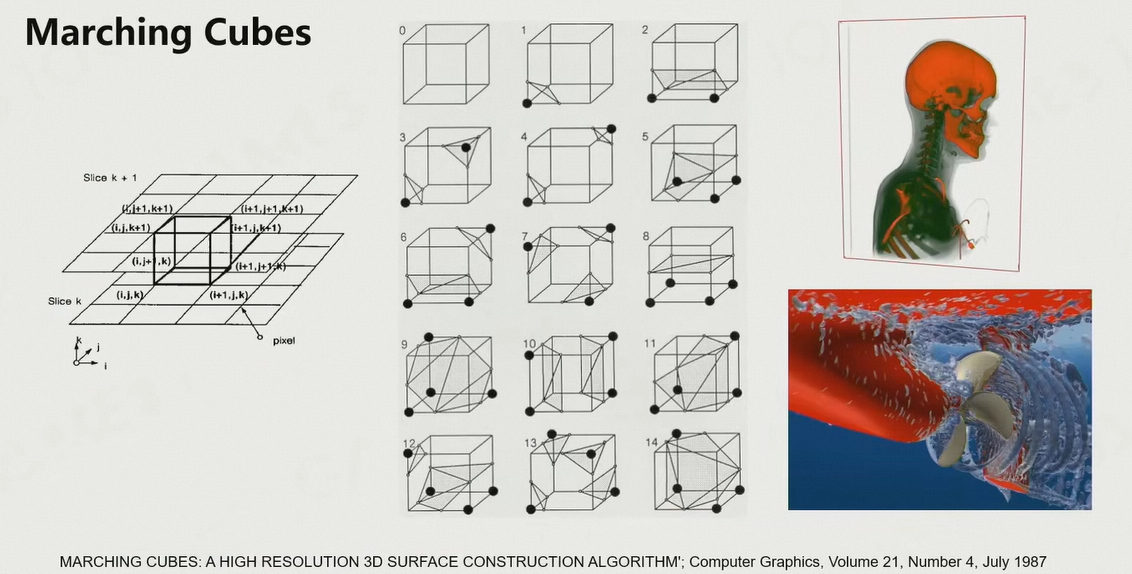
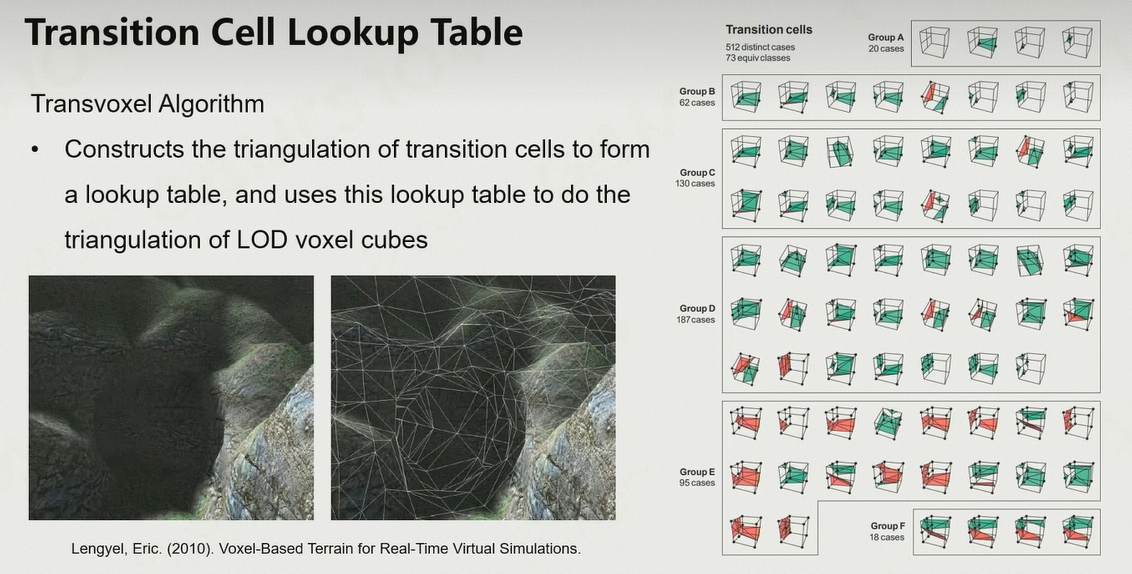
- 将地形表示为三维空间,三维空间中的每个点存一个权重值,表示这个位置是否有物质、物质的密度
- 通过Marching Cubes方法,找到等值面,切分立方体,形成一个水密的三角面片集,把形状表达出来
6.2 地形的材质
6.2.1 Texture Splatting


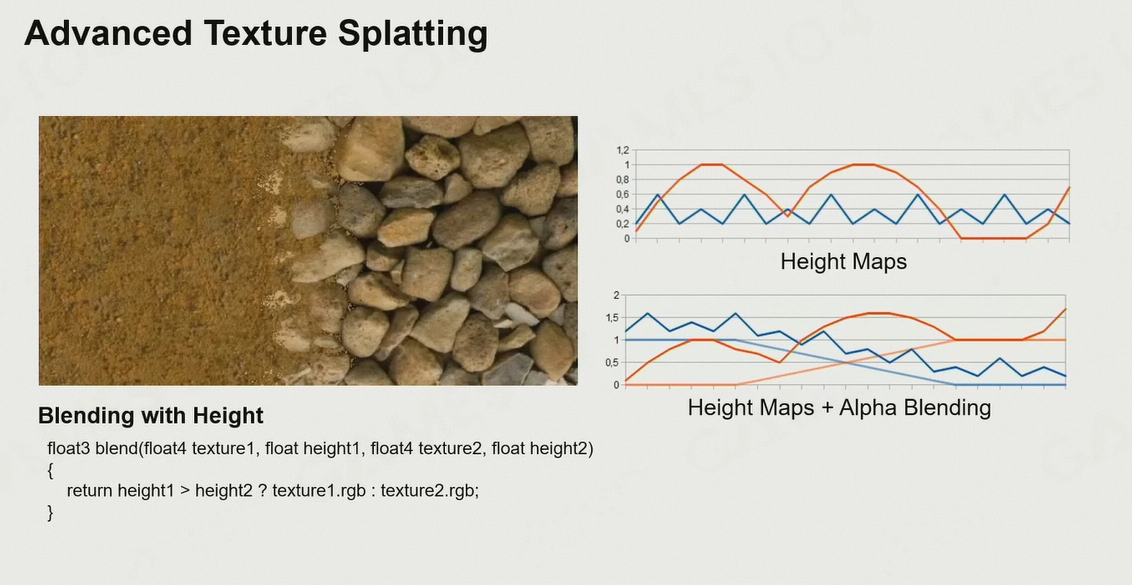
- 每个材质存储Base Color、Normal、Roughness、Height四种贴图
- 再存储一张混合贴图,每个channel表示一种贴图的权重,通过笔刷设置不同材质的权重
- 在过渡的时候,如果需要混合两种材质,则根据height对权重进行调整,height高的权重下降慢
- 缺点:由于是01切换,当相机移动的时候,会有很多抖动,导致分界线过硬
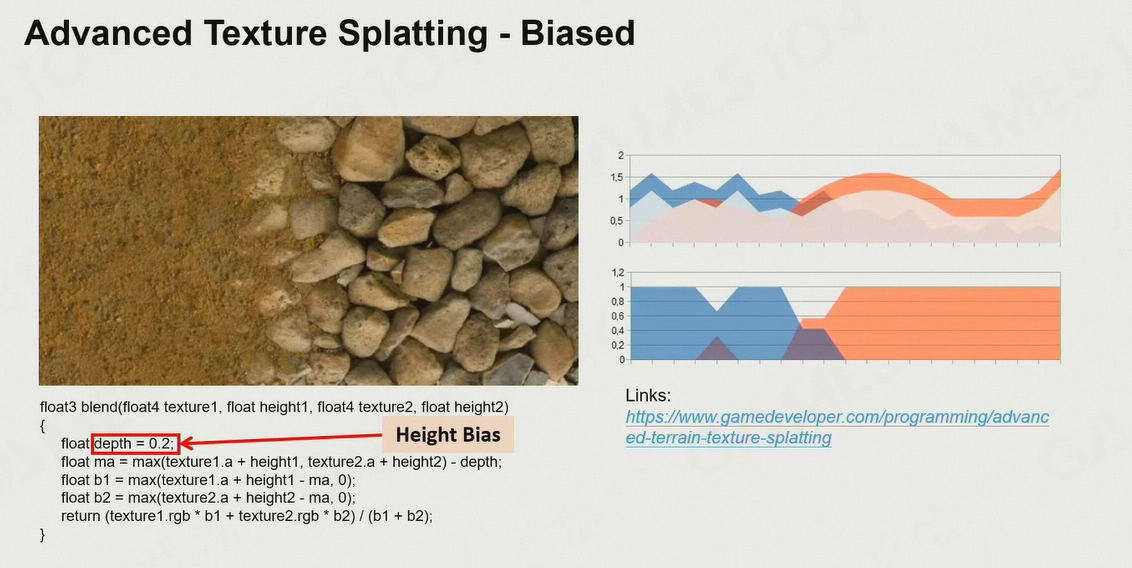
- 解决方法:添加一个bias,当两者高度差<bias的时候,用权重进行插值
6.2.2 在Texture Array中采样
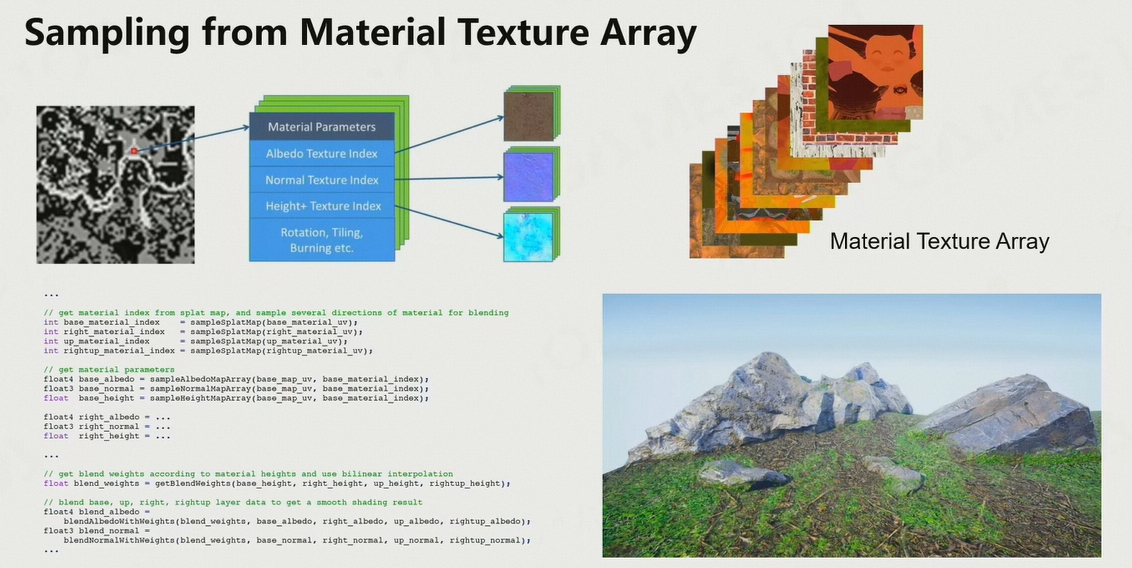
- 将地表的多种材质存储为一个数组,每次采样仅会采样其中一个材质
- 混合的时候,根据位置、权重、index,判断采样哪种材质,采样的权重是但多少
6.2.3 Displacement Mapping

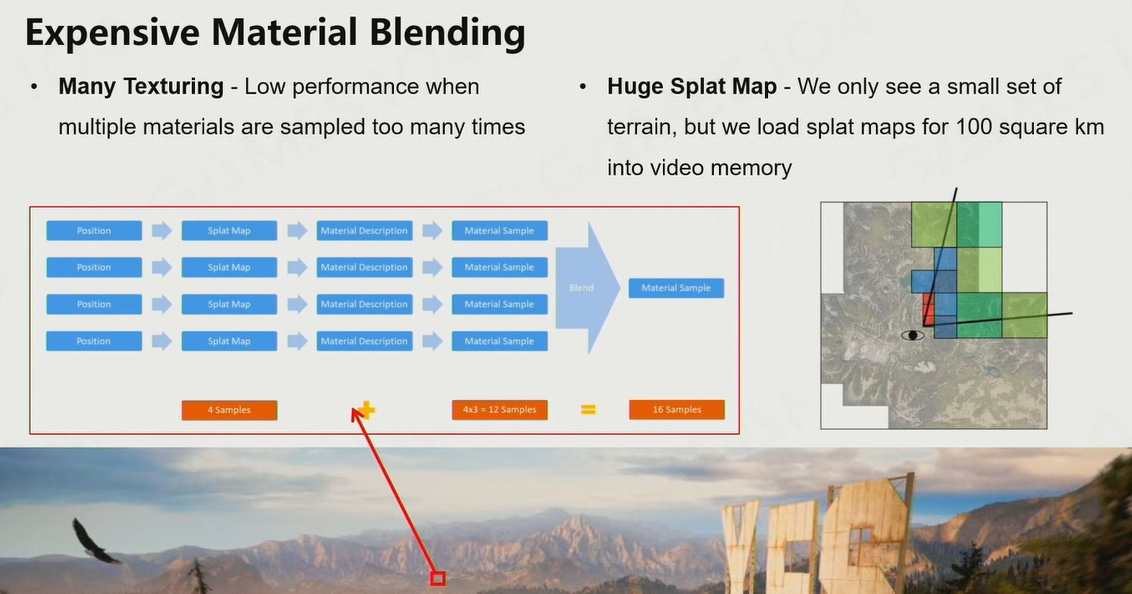
6.2.4 Expensive Material Blending
- 每一次进行纹理采样,都需要采样8个点,进行7次插值
- 一个点有几种材质进行混合,就需要在上述基础上乘几
- 而这些采样的数据在内存中的不同地方,address的不停跳跃会非常浪费时间
- 事实上,我们看到的地形仅有地形的一部分,其他部分都会被裁剪掉
6.2.5 Virtual Texture
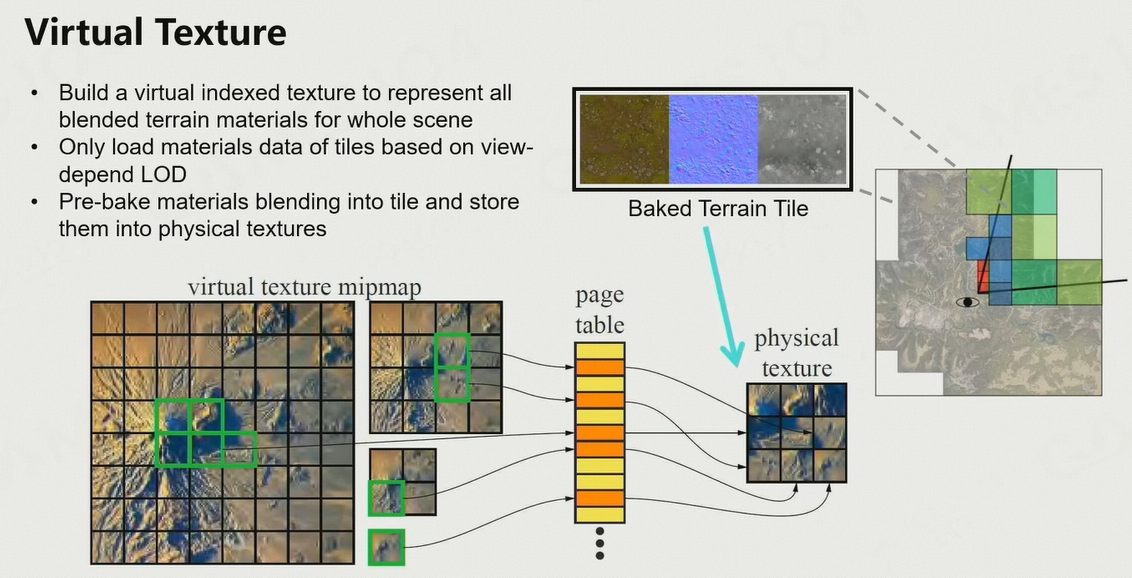
核心思想:将用到的东西装载到内存中
- 将纹理分为不同块,分块数满足2的幂次
- 然后根据分块对纹理建立Mipmap
- 绘制时,只将看到的纹理LOD层加载到内存
6.2.6 浮点数精度溢出
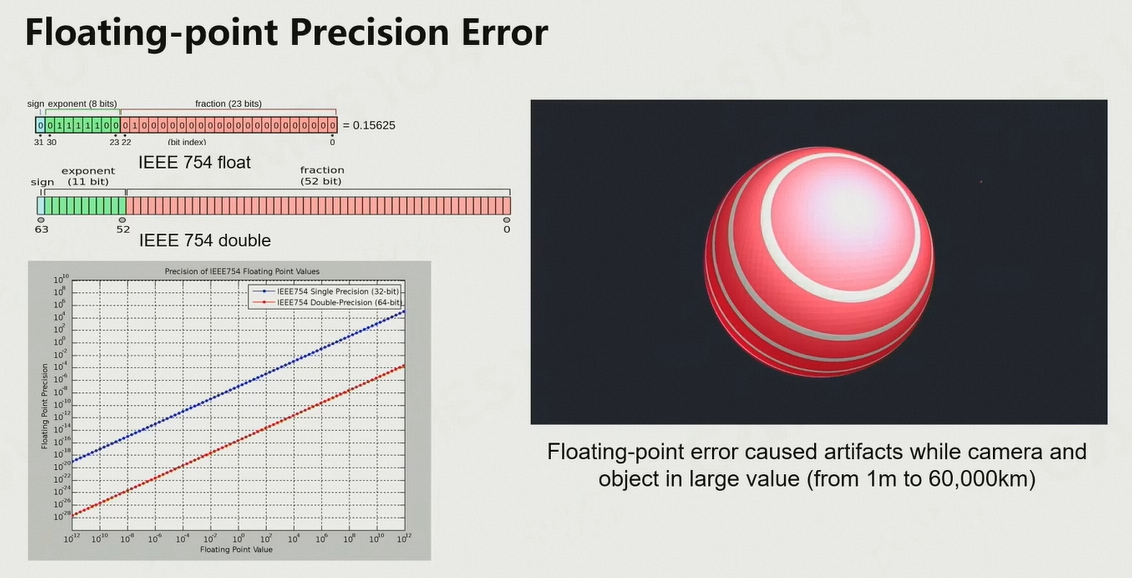
- 当摄像机&地形的全局坐标很大(如1km),而地形上的物体与地形距离很近(如0.5m)的时候,远处的地形与物体就会由于精度问题产生抖动

- 解决方法:
- 将相机的位置强行设置为0,地形的位置坐标根据相机的位置设置,此时两者使用到的坐标都不会很大,就可以保证小数点后的精度了
- 修改前:地形位置1000010m、物体位置1000010.5m、相机位置1000000m
- 修改后:地形位置10m、物体位置10.5m、相机位置0m
- 也可以将整个大型关卡切分为不同的小关卡,每个小关卡拥有自己的全局坐标系
- 将相机的位置强行设置为0,地形的位置坐标根据相机的位置设置,此时两者使用到的坐标都不会很大,就可以保证小数点后的精度了
6.3 植被道路贴花等
6.3.1 树木渲染

6.3.2 装饰物渲染 Decorator
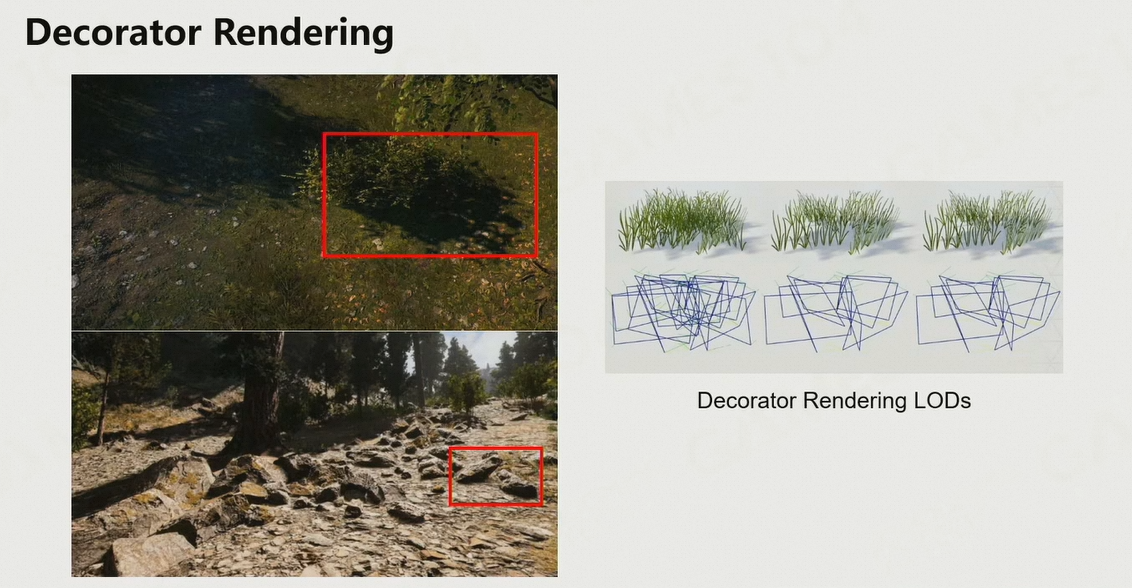
6.3.3 道路和贴画渲染

- 将地形的纹理、道路的纹理、贴画的纹理全部放到Virtual Texture中,runtime的时候直接调用virtual texture即可
- 计算的复杂度集中在bake中,runtime的时候只需要将纹理贴上去即可,开销很低
6.4 大气散射理论
6.4.1 Analytic Atmosphere Apperance Modeling
\[ F(\theta,\gamma)=(1+Ae^{\frac{B}{\cos\theta+0.01}})·(C+De^{E\gamma}+F\cos^2\gamma+G·\chi(H,\gamma)+I\cos^{\frac{1}{2}}\theta) \\ L_\lambda=F(\theta,\gamma)·L_{M\lambda} \]
优点:
- 便于计算
缺点:
- 只能在地表
- 参数是写死的,无法自由的更改
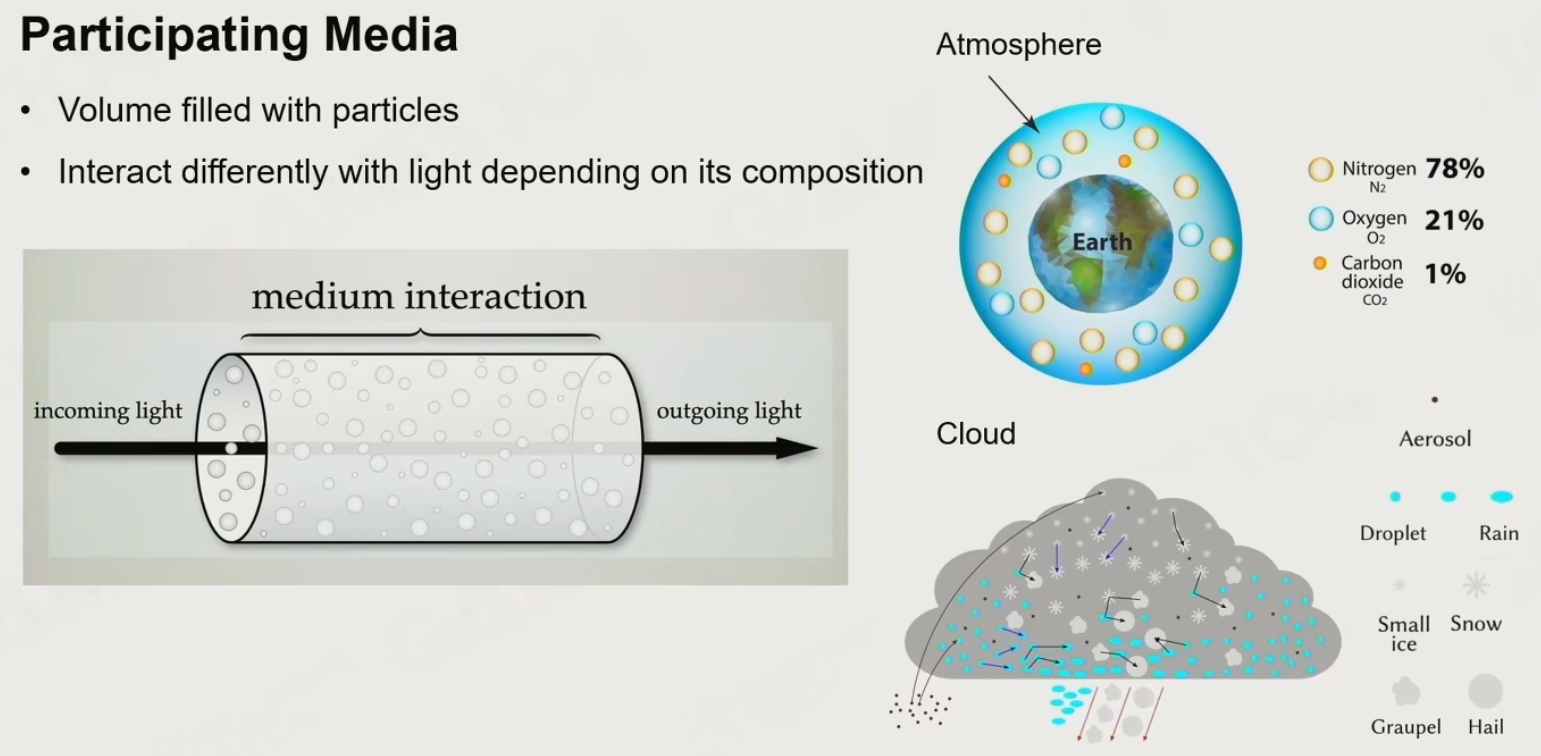
6.4.2 Participating Media
空气是由两种粒子构成的:
- 各种气体分子:如N2、O2、CO2
- 气溶胶:空气中的灰尘形成的小的气溶胶分子
6.4.3 光与Participating Media的交互:Radiative Transfer Function (RTF)
- 吸收:\(-\sigma_\alpha L(x,\omega)\)
- 散射:\(-\sigma_sL(x,\omega)\)
- 自发光:\(\sigma_\alpha L_e(x,\omega)\)
- 其他气体分子的影响:\(\sigma_s\int_{S^2}f_p(x,\omega,\omega')L(x,\omega')d\omega'\)
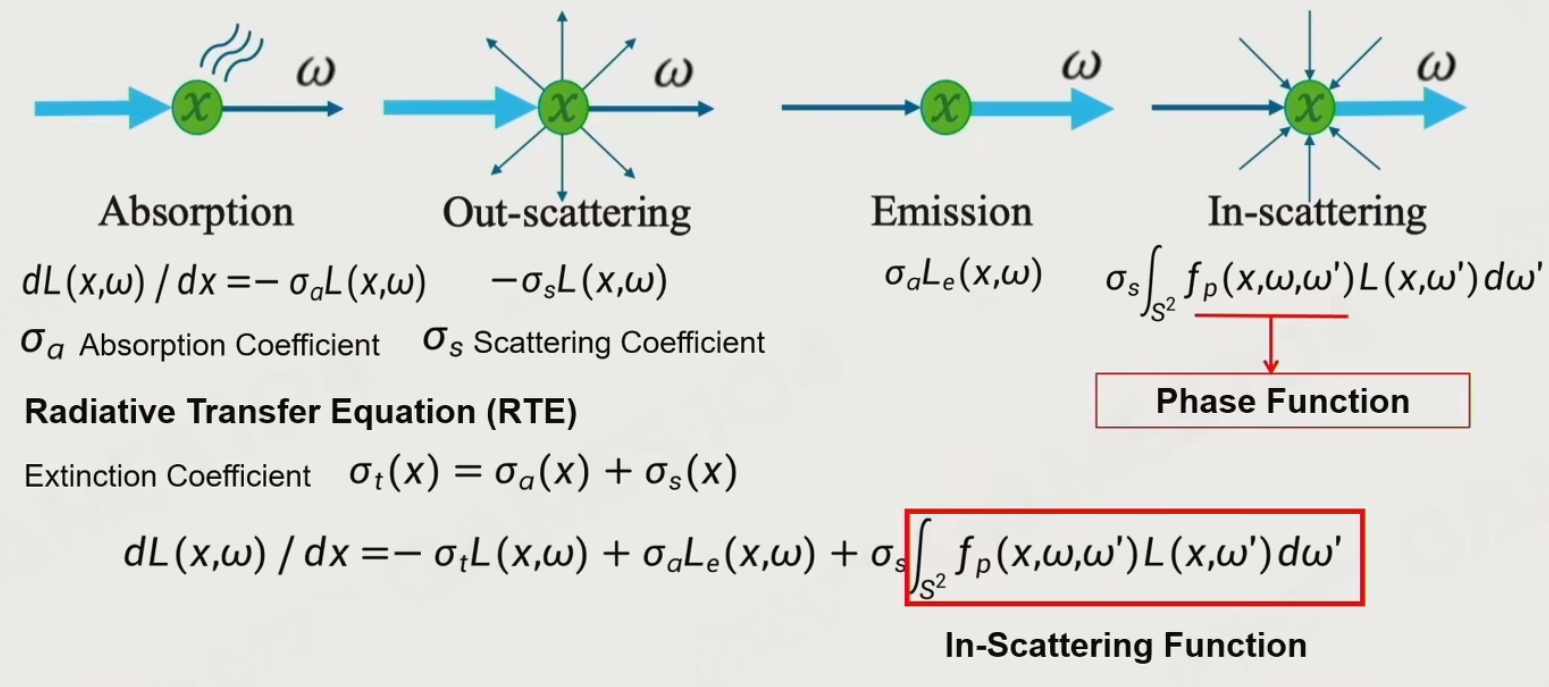
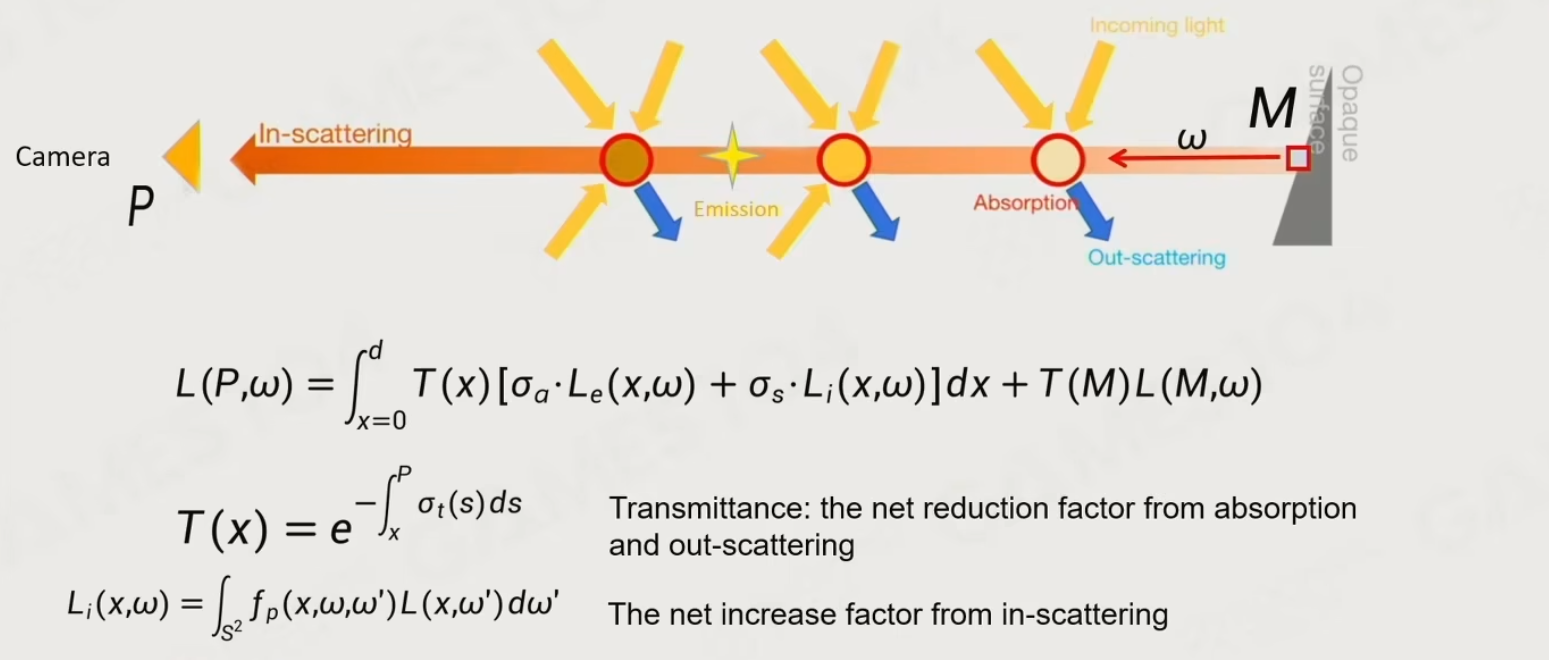
6.4.4 Volume Rendering Equation (VRE)
- Transmittance 通透度:在M点看到的东西,由多少会保留到在P点看到的东西,是路径积分的结果
- scattering function 散射方程:从M点到P点,叠加的其他粒子的效果
6.4.5 大气的实际物理
- 太阳光由不同波长的光组成
- 大气由两种粒子构成:
- 气体分子:直径小于光的波长
- 气溶胶分子:直径接近于光的波长
6.4.5.1 散射
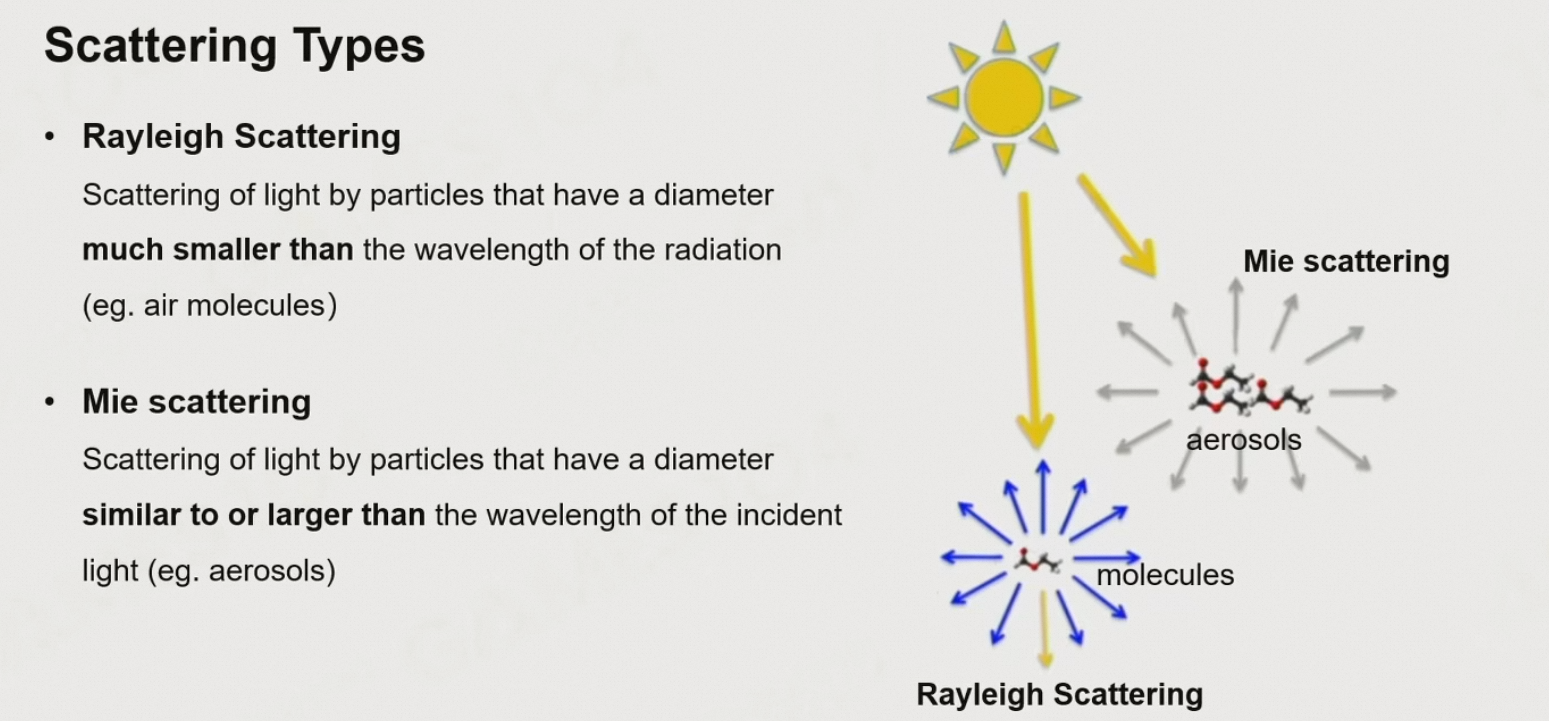
两种散射类型
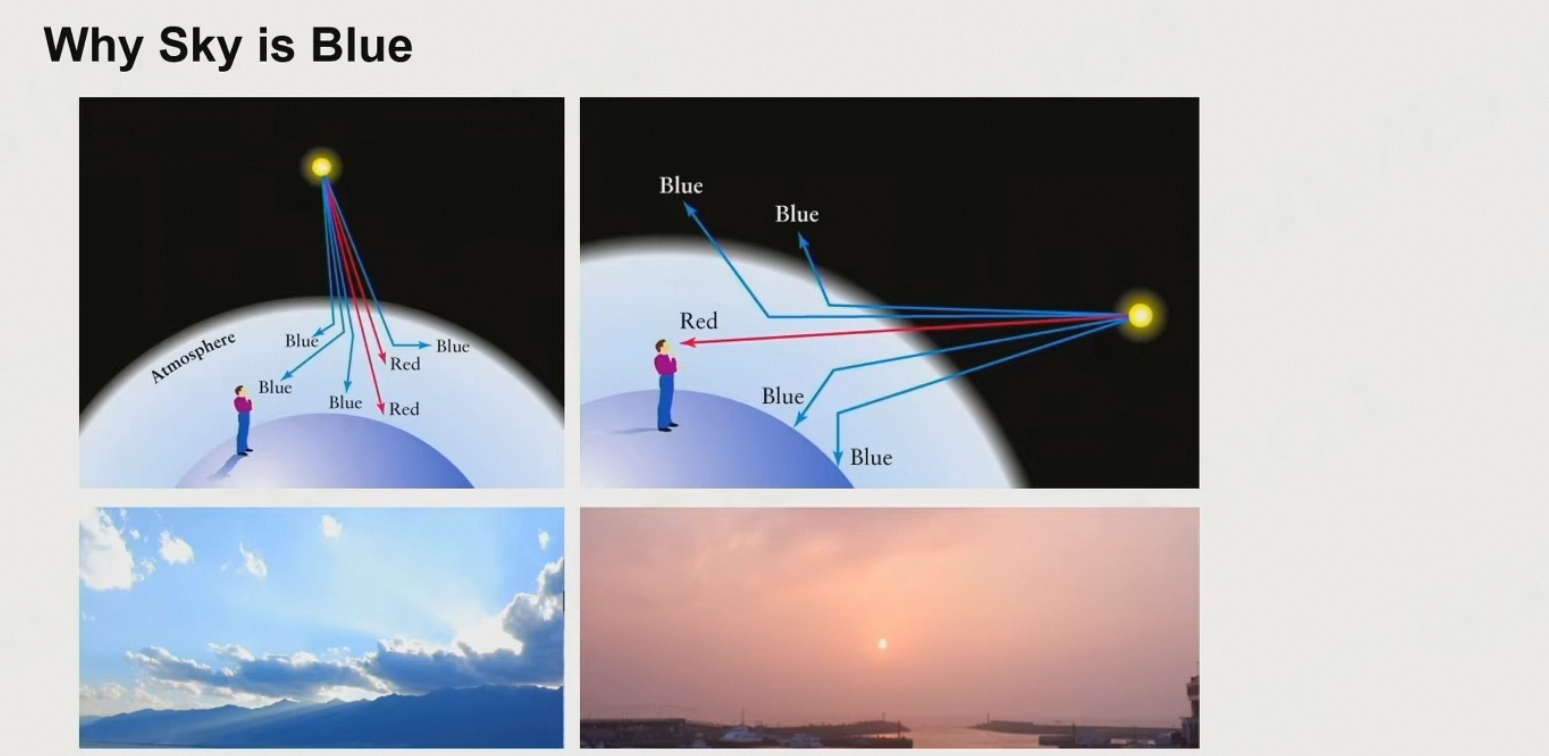
瑞利散射:当粒子的直径远小于光的波长的时候,光会均匀散射,波长越短散射越明显
- \(\lambda\):光的波长
- \(\theta\):观察方向与光方向的夹角
- \(h\):海拔高度

幂散射:当粒子的直径接近或大于光的波长的时候,光的散射会有方向性,且对波长不敏感
- \(\lambda\):光的波长
- \(\theta\):观察方向与光方向的夹角
- \(h\):海拔高度
- \(g\):几何参数,由艺术家调整
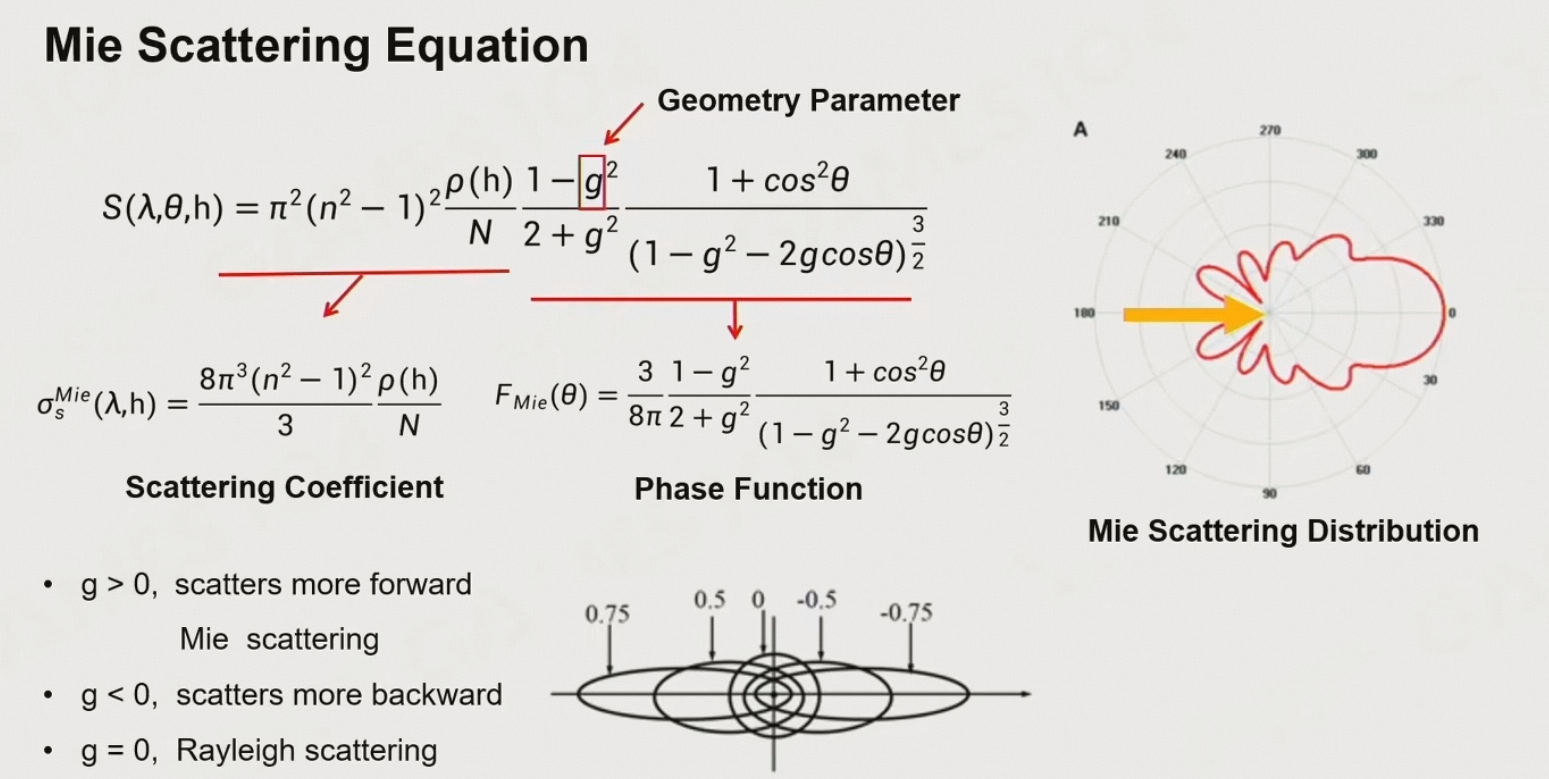

6.4.5.2 吸收
- O3:吸收红光、橙光、黄光
- CH4:吸收红光
- 假设大气中的O3、CH4均匀分布

6.4.6 单次散射 & 多次散射
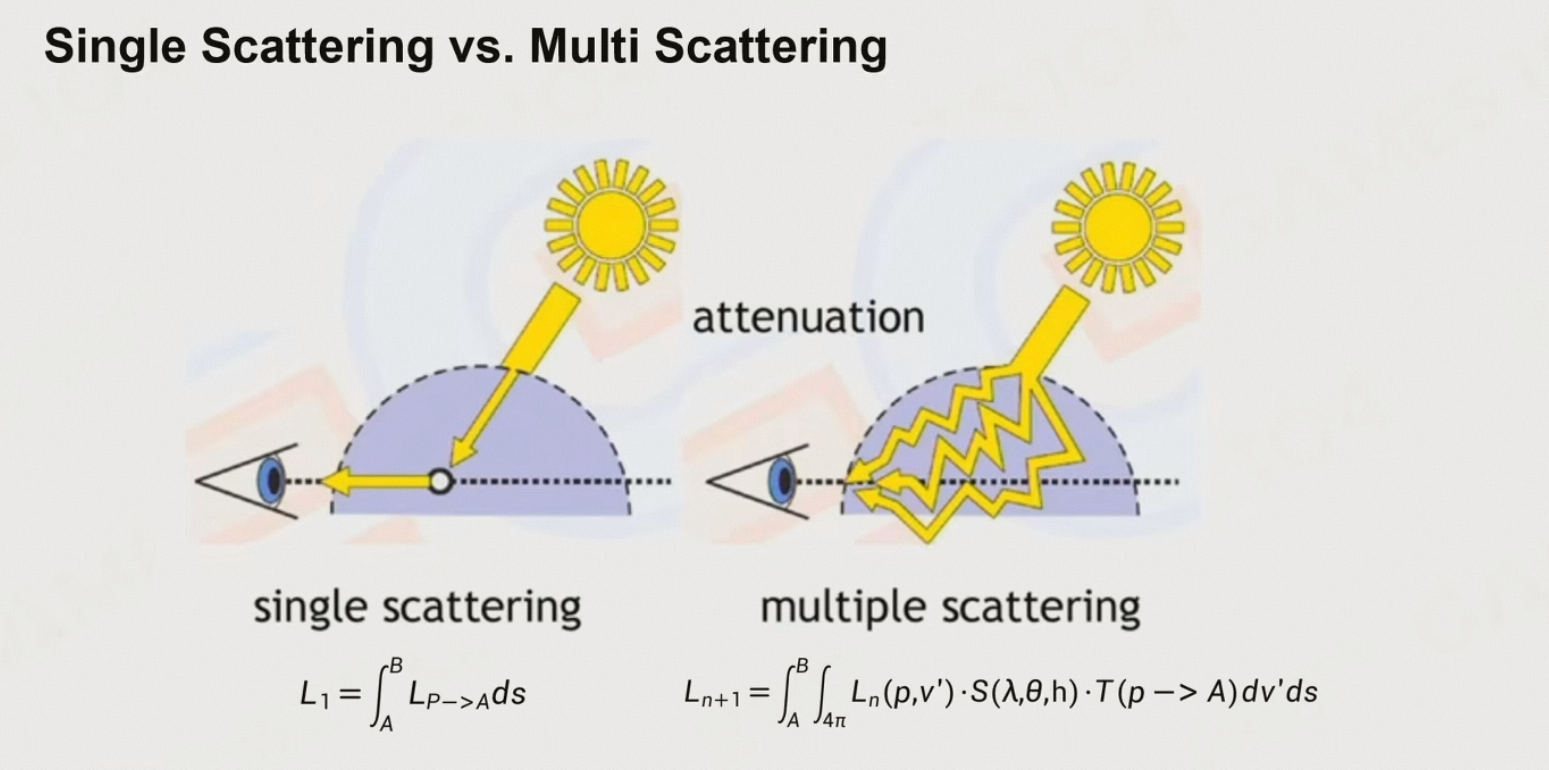
6.4.7 Ray Marching
- 沿着一条视线,均匀地采很多点,把沿途的效果一步一步地积分起来
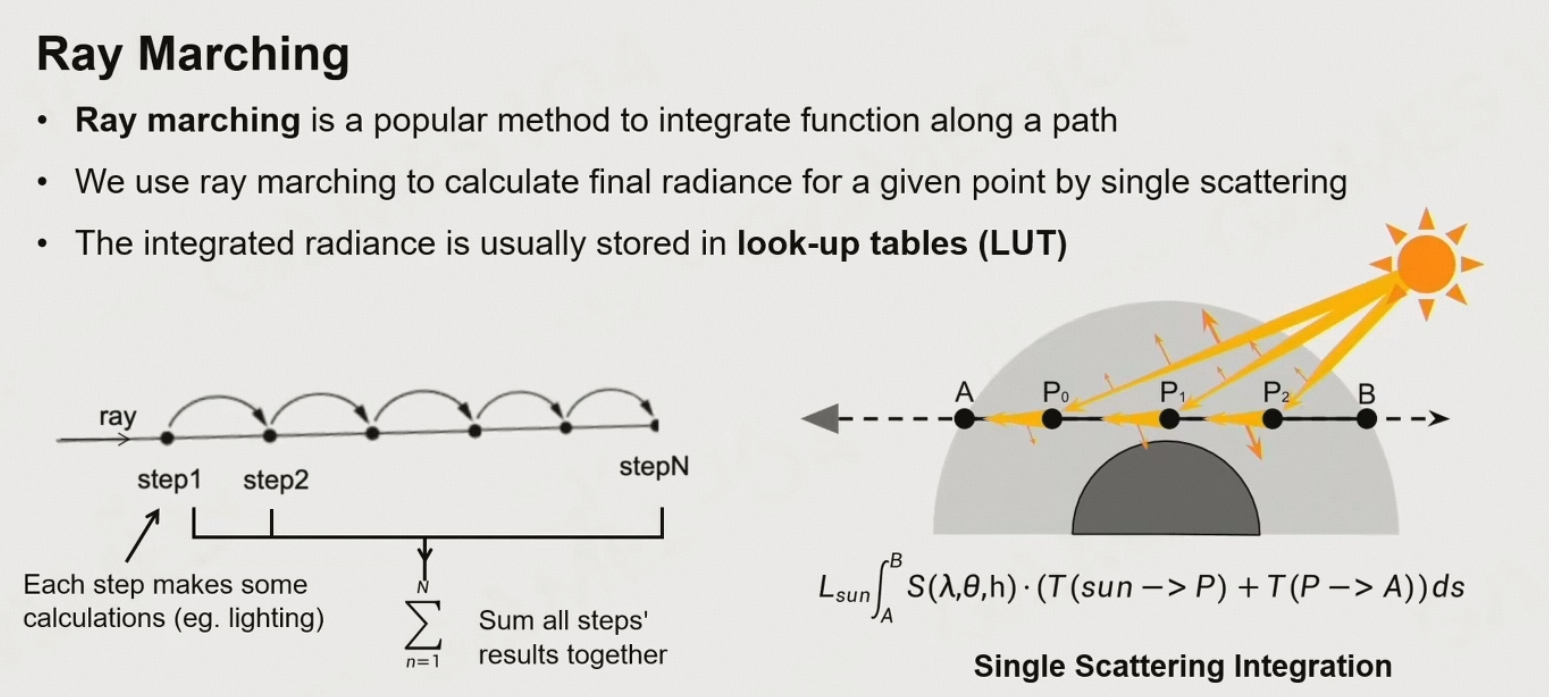
6.5 实时大气渲染
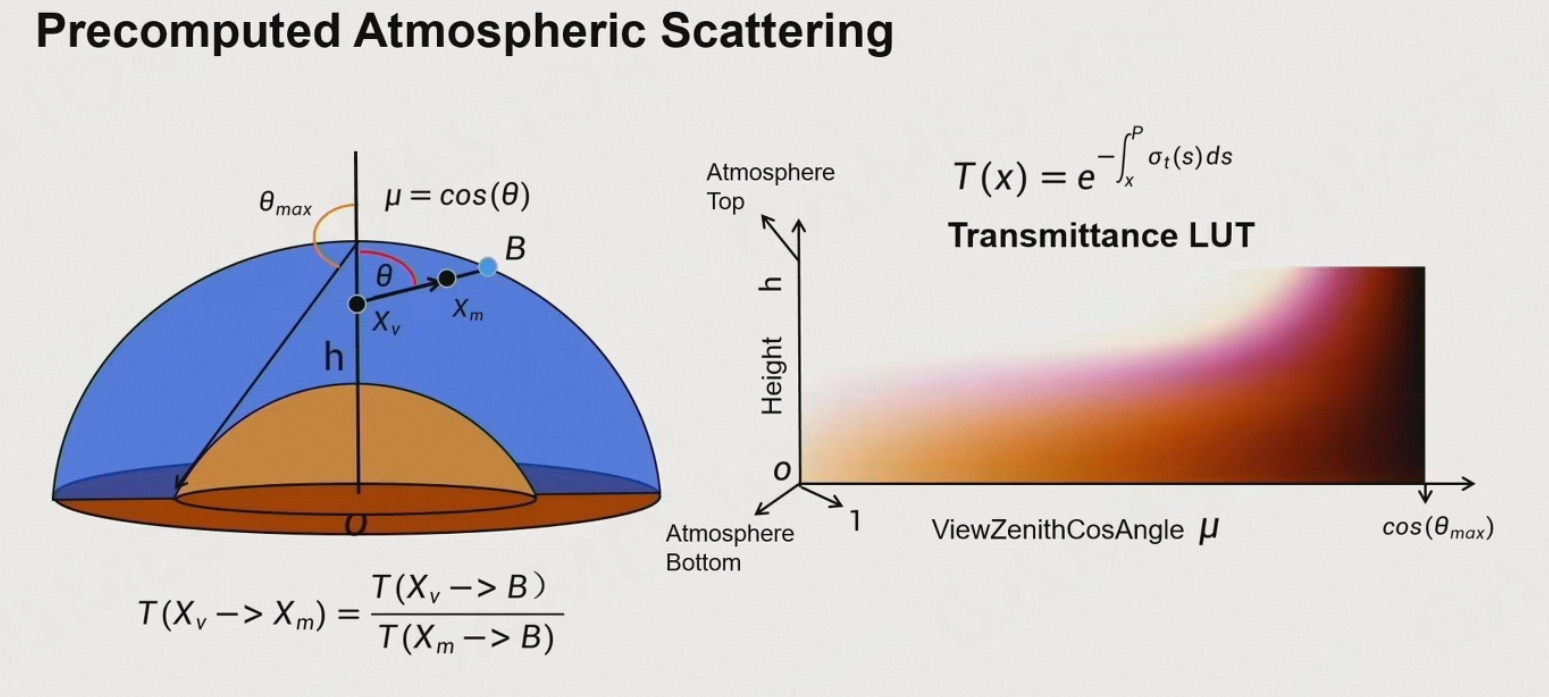
6.5.1 Transmittance LUT \((\mu,r)\)
- 选择一个海拔高度为\(h\)的点,在当前海拔高度存储两个值
- 视线和天顶之间的夹角为\(\theta\),用\(\cos\theta\)进行参数化表达
- 从当前点\(X_v\)出发,沿视线方向走到大气层的边界,与边界的交点为\(B\)
- 此时,我们可以计算出整个大气层的通透度,即:\(T(X_v → B)\)
- 假设在远处有一个物体在点\(X_m\)处发出光,则该处的光到达当前点\(X_v\)的通透度为:\(T(X_v→X_m)=\frac{T(X_v→B)}{T(X_m→B)}\)
- 此时,我们可以通过一个简单的二维方程,通过除法,即可表达原先的四维方程
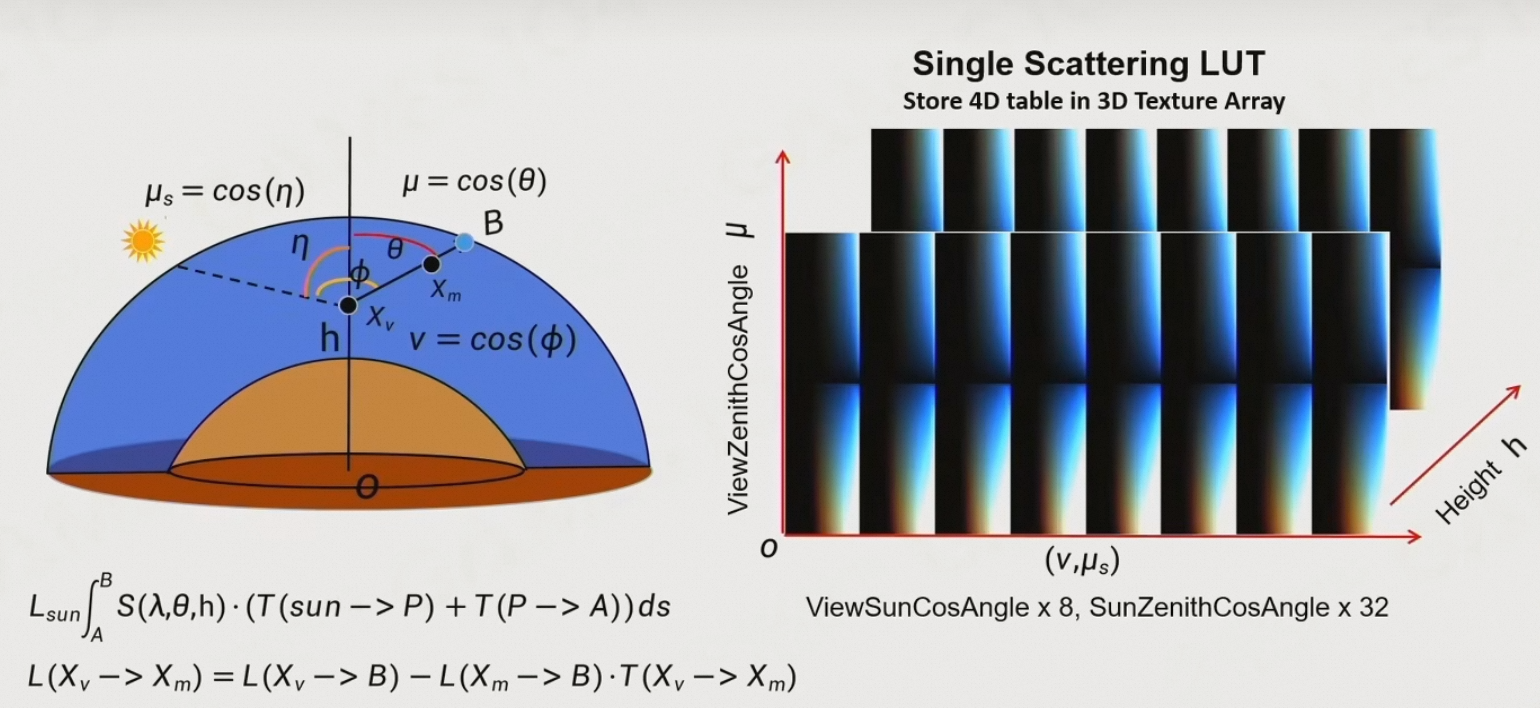
6.5.2 Single Scattering LUT \((v,\mu_s,\mu,r)\)
- 视线方向:\(\theta\)
- 选择一个海拔高度为\(h\)的点\(X_v\),朝着一个方向去看,此时可以得到天顶角\(\theta\)
- 由于大气层是个球,因此有了起点和方向,即可得知\(B\)与\(X_v\)的距离
- 太阳到天顶的角度为:\(\eta\)
- 视线与太阳之间的夹角:\(\phi\)
- 如果大气层各项同性,则只需要存储\((\theta,\eta,\phi)\)对应的散射,即可得到某个点看向太空中的点的Single Scattering
- 再沿着高度\(h\)进行采样,即可得到一个四维表,可以将其存储到3D Texture Array中
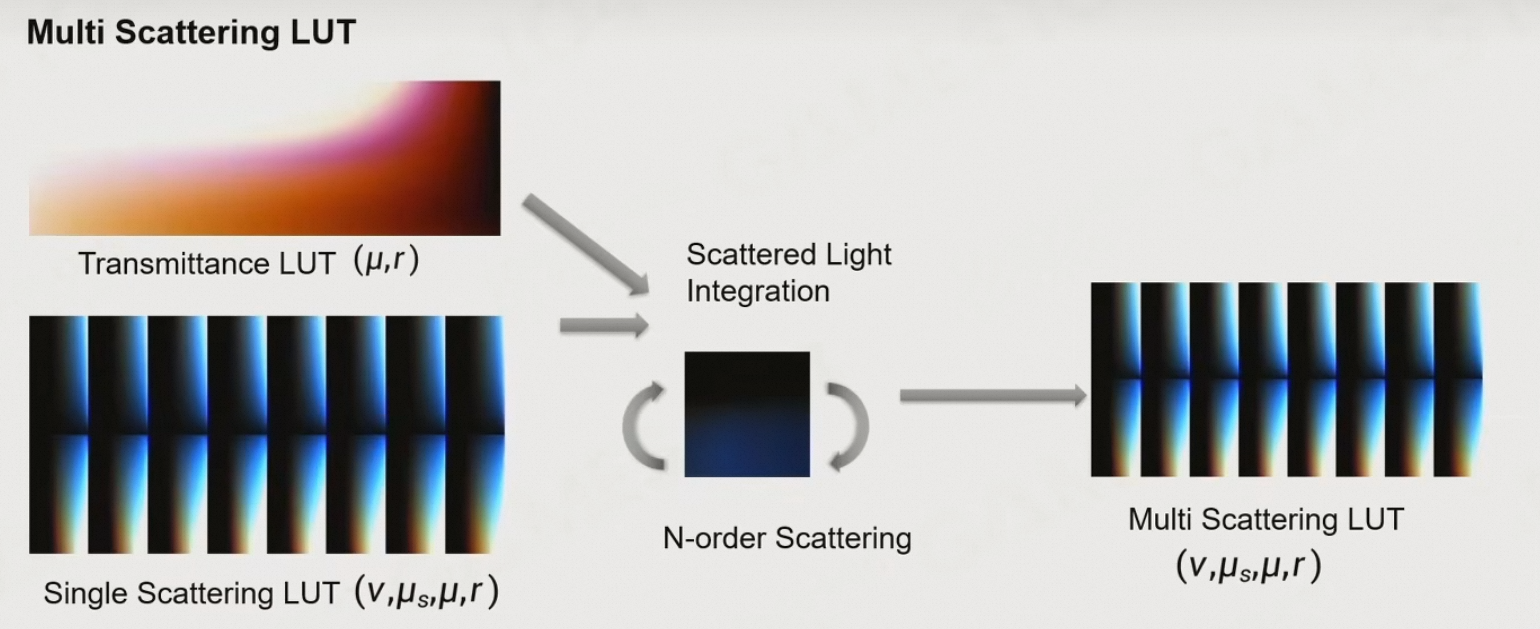
6.5.3 计算Multi Scattering
- 将Single
Scattering照亮的点,通过Transmittance进行多次积分,即可得到Multi
Scattering
- 通常只做3~4次
6.5.4 缺点
- 预计算的计算量很大
- 场景变化后,需要重新计算:如天空忽然开始下雨,设计场景时更改参数的值
- 实时计算时,需要做很多次高维表查值,导致时间开销较大
6.5.5 Production Friendly Quick Sky and Atmosphere Rendering
假设:在空气中的散射是低频的,对空气中的一个分子,来自于不同方向的散射在各向分布都是同样的
从而会导致每个分子的多次散射,实际上是一个等比衰减,比例可以通过计算两次&三次散射得到
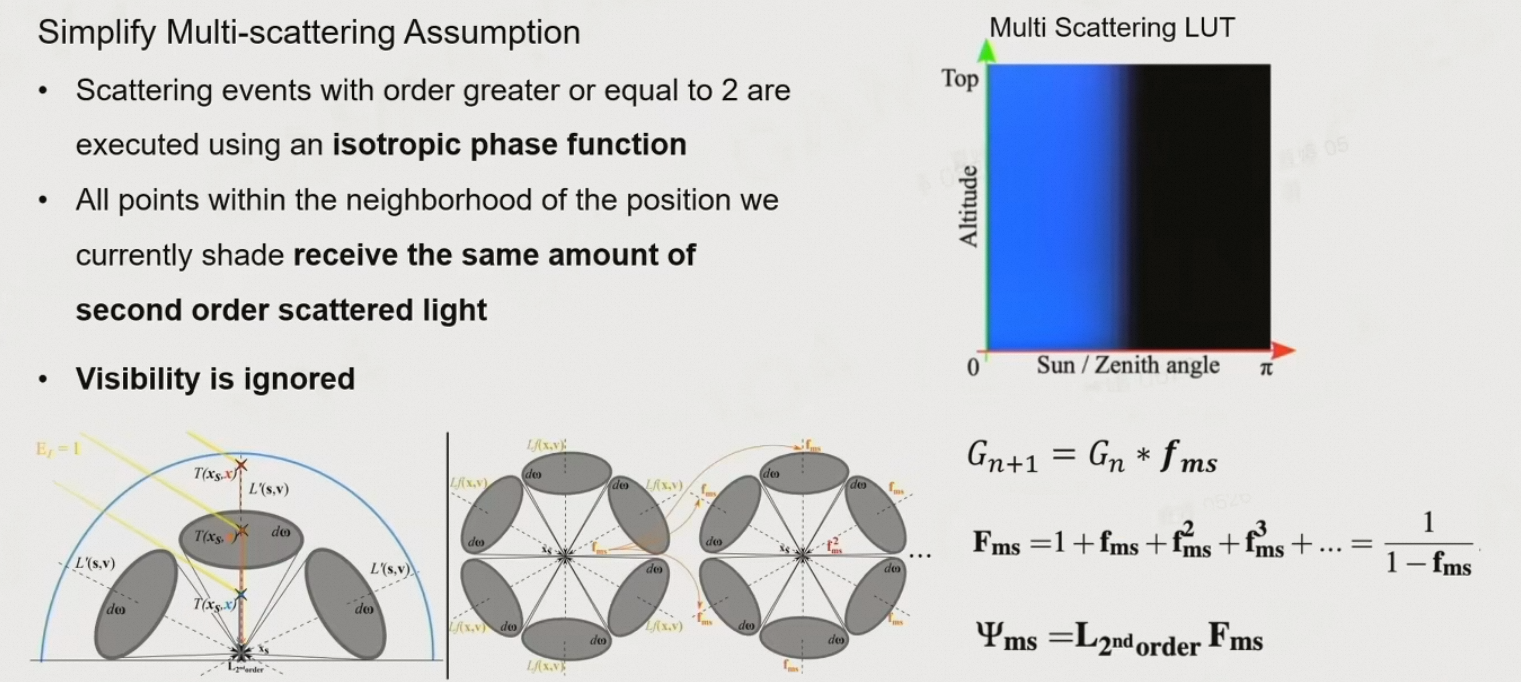
由于每一帧都要计算LUT,因此可以假设太阳位置不变、角色位置不变,从而可以删除两维


6.6 云的渲染
6.6.1 云的类型
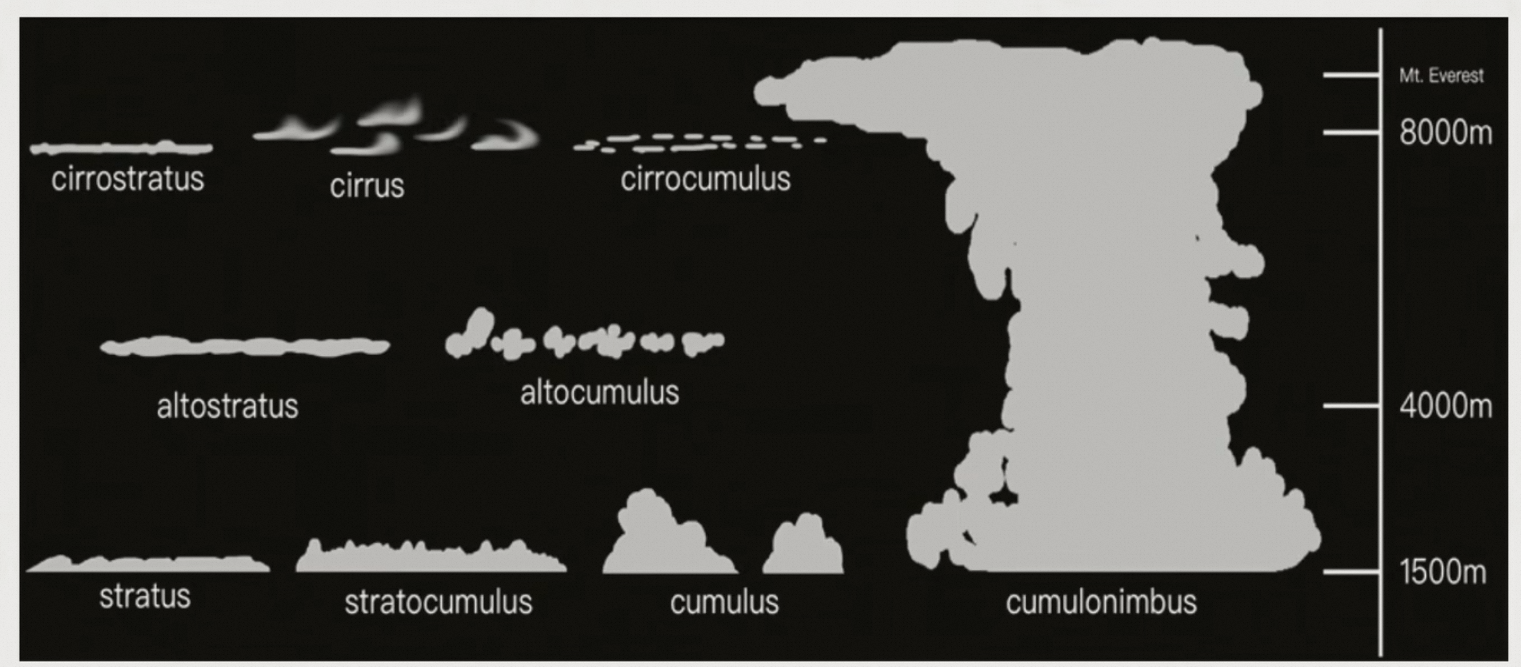
6.6.2 Billboard Cloud
通过大量2D图片的混合,实现云的效果

6.6.3 Volumetric Cloud Modeling

6.6.3.1 Weather Texture
- 云的随机分布
- 云的厚度:0~1的值
让云飘起来:对Weather Texture进行平移
让云产生变化:对Weather Texture进行扰动

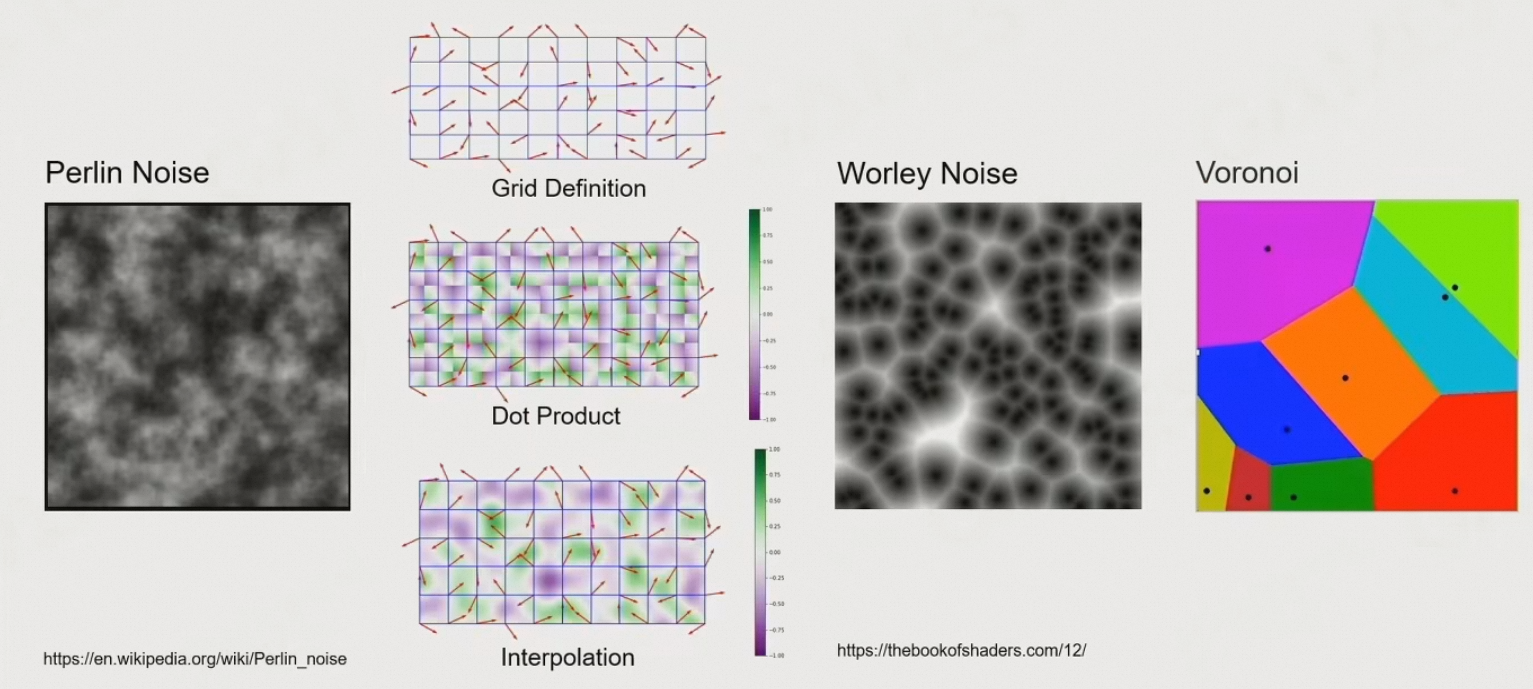
6.6.3.2 Noise Function
Perlin噪声:在多项式时间内产生棉花絮之类的效果
Worley噪声:形成泡泡絮的效果
6.6.3.3 Cloud Density Model
- 基础的云是柱状的,需要添加噪声优化效果
- 先用低频噪声,删除一部分
- 在添加高频的细节
- 从而可以模拟数学上的分形效果

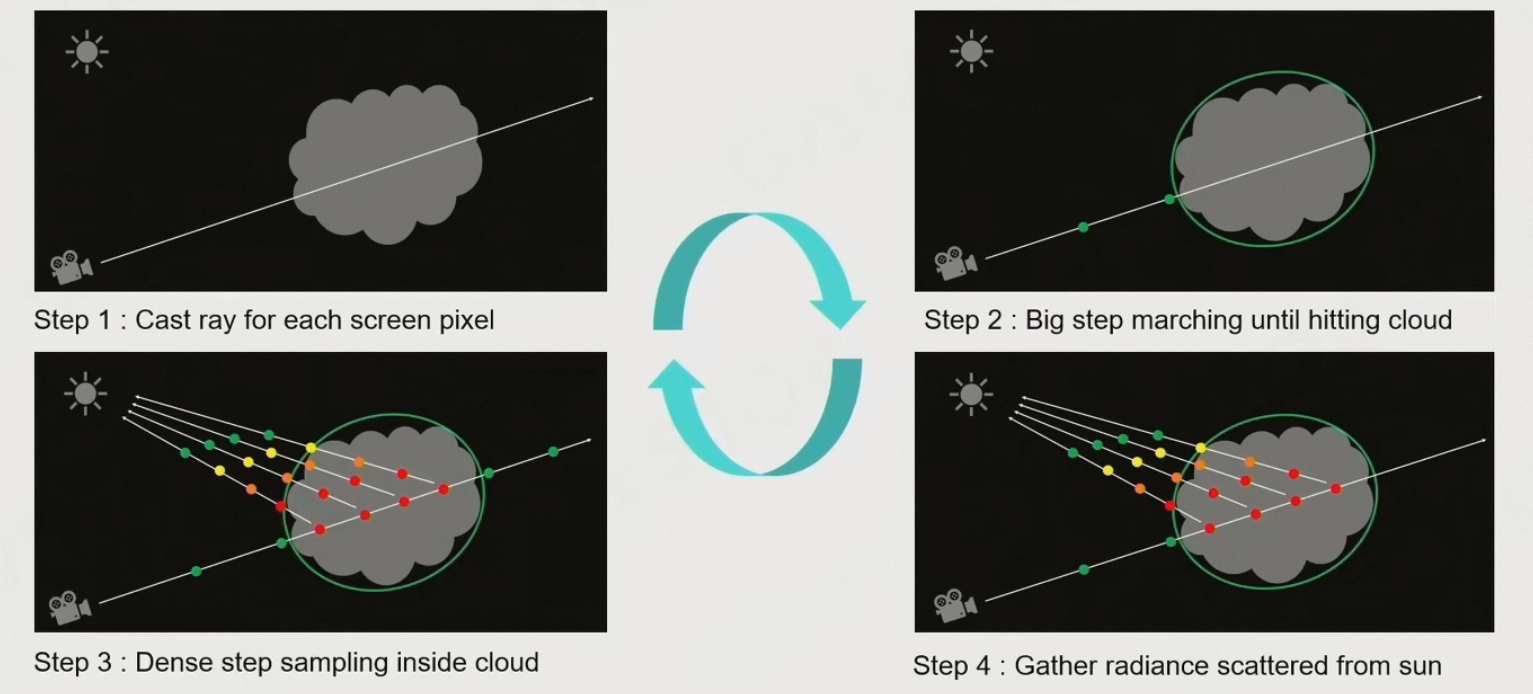
6.6.3.4 Rendering Cloud by Ray Marching
- 从相机发送射线,判断是否能打到云上
- 开始时步长较大
- 一旦与云相交,就缩小步长,在每一个点计算大气的通透和散射
- 由于云的通透度很低,因此可以做大量假设,简化渲染方程
- 天空中的云实际上是GPU中的一个3D纹理,通过Ray Marching的方法解析该纹理的结果
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 华风夏韵!
评论